排序算法之高效排序:快速排序,归并排序,堆排序详解

排序算法之高效排序：快速排序、归并排序、堆排序详解

前言
[一、快速排序（Quick Sort）](#一、快速排序（Quick Sort）)
- [1.1 算法原理](#1.1 算法原理)
- [1.2 代码实现（Python）](#1.2 代码实现（Python）)
- [1.3 性能分析](#1.3 性能分析)
[二、归并排序（Merge Sort）](#二、归并排序（Merge Sort）)
- [2.1 算法原理](#2.1 算法原理)
- [2.2 代码实现（Java）](#2.2 代码实现（Java）)
- [2.3 性能分析](#2.3 性能分析)
[三、堆排序（Heap Sort）](#三、堆排序（Heap Sort）)
- [3.1 算法原理](#3.1 算法原理)
- [3.2 代码实现（C++）](#3.2 代码实现（C++）)
- [3.3 性能分析](#3.3 性能分析)
四、三种高效排序算法的对比与适用场景
总结

前言

相较于上一期我讲的冒泡、选择、插入等基础排序，快速排序、归并排序和堆排序凭借更优的时间复杂度，成为处理大规模数据排序任务的首选方案。本文我将深入剖析这三种高效排序算法的原理、实现细节、性能特点及适用场景，助力你掌握它们在实际开发中的应用技巧。

一、快速排序（Quick Sort）

1.1 算法原理

++快速排序++由托尼・霍尔（Tony Hoare）于 1959 年提出，是一种基于分治思想的排序算法。其核心步骤如下：

选择基准值：从数组中选取一个元素作为基准值（通常选择第一个、最后一个或中间元素）。

分区操作：将数组分为两个子数组，使得左边子数组的所有元素都小于等于基准值，右边子数组的所有元素都大于基准值。

递归排序：对左右两个子数组分别递归地进行快速排序。

通过不断重复上述步骤，最终使整个数组达到有序状态。例如，对于数组[5, 3, 8, 6, 2]，若选择5作为基准值，经过分区操作后，数组变为[3, 2, 5, 6, 8]，然后分别对[3, 2]和[6, 8]进行递归排序，最终得到有序数组[2, 3, 5, 6, 8]。

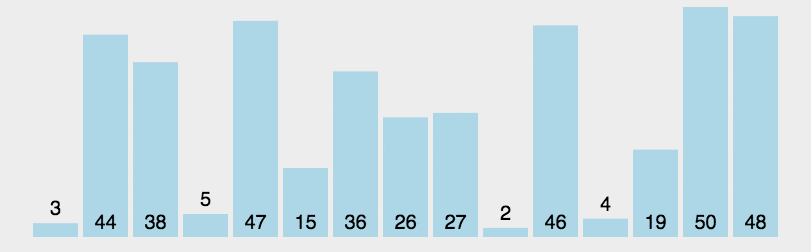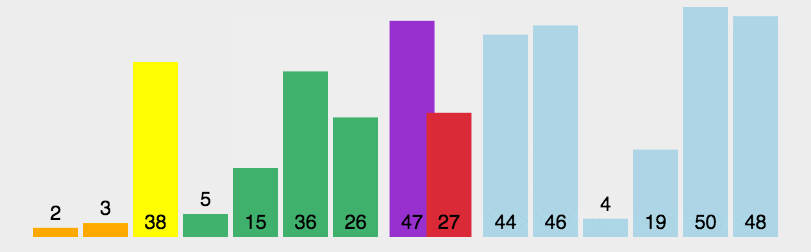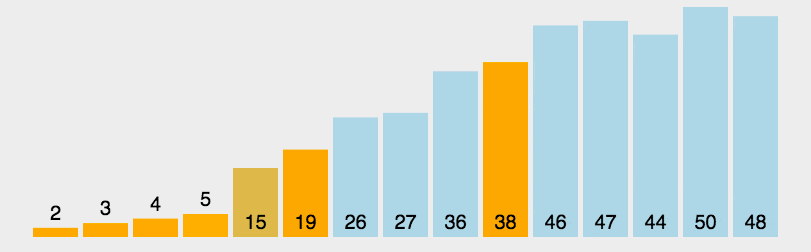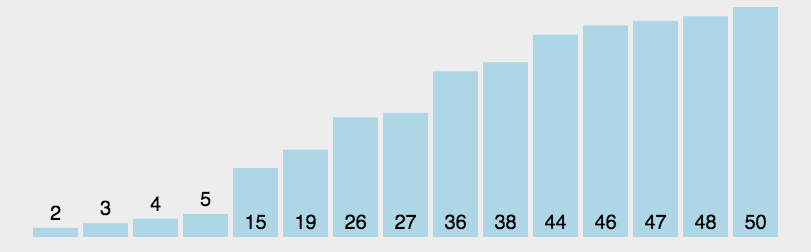
1.2 代码实现（Python）

python 复制代码

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quick_sort(left) + middle + quick_sort(right)

上述代码中，首先判断数组长度，若小于等于 1 则直接返回。接着选取基准值，通过列表推导式将数组分为小于、等于、大于基准值的三个部分，最后递归地对左右子数组进行排序并合并。

1.3 性能分析

时间复杂度：

平均情况下，快速排序的时间复杂度为 O ( n log ⁡ n ) O(n \log n) O(nlogn) ，其中n为数组元素个数。

最坏情况下（如数组已有序且每次选择的基准值为最大或最小元素），时间复杂度退化为 O ( n 2 ) O(n^2) O(n2) 。

空间复杂度 ：快速排序的空间复杂度主要取决于递归调用栈的深度。平均情况下，空间复杂度为 O ( log ⁡ n ) O(\log n) O(logn) ；在最坏情况下，递归深度达到n，空间复杂度为 O ( n ) O(n) O(n) 。

稳定性：快速排序是不稳定的排序算法，因为在分区过程中，相同元素的相对顺序可能会发生改变。

二、归并排序（Merge Sort）

2.1 算法原理

++归并排序++同样基于分治思想，它将一个数组分成两个大致相等的子数组，分别对两个子数组进行排序，然后将排好序的子数组合并成一个最终的有序数组。具体步骤如下：

分解：将待排序数组不断平均分成两个子数组，直到子数组长度为 1（单个元素可视为有序）。

排序：对每个子数组进行排序（可使用其他排序方法，通常也是递归地使用归并排序）。

合并：从最底层开始，将两个有序的子数组合并成一个更大的有序数组，不断向上合并，直至得到整个有序数组。

例如，对于数组[8, 4, 2, 1, 7, 6, 3, 5]，先分解为多个子数组，再依次排序并合并，最终得到有序数组[1, 2, 3, 4, 5, 6, 7, 8]。

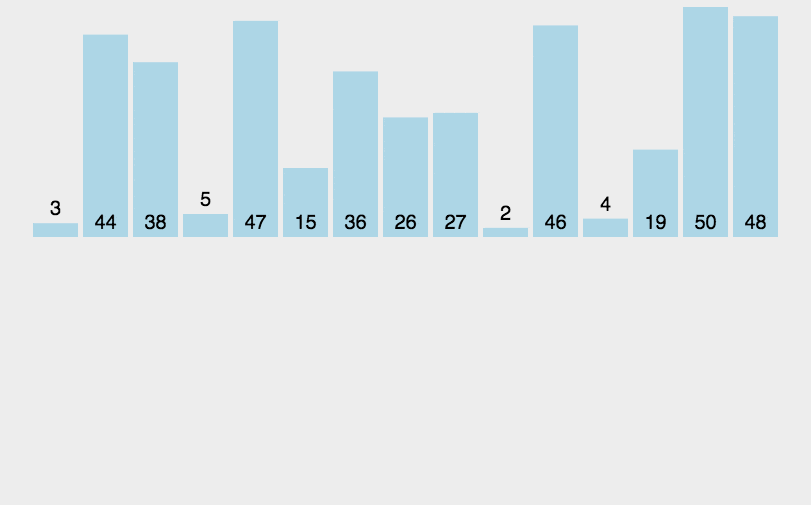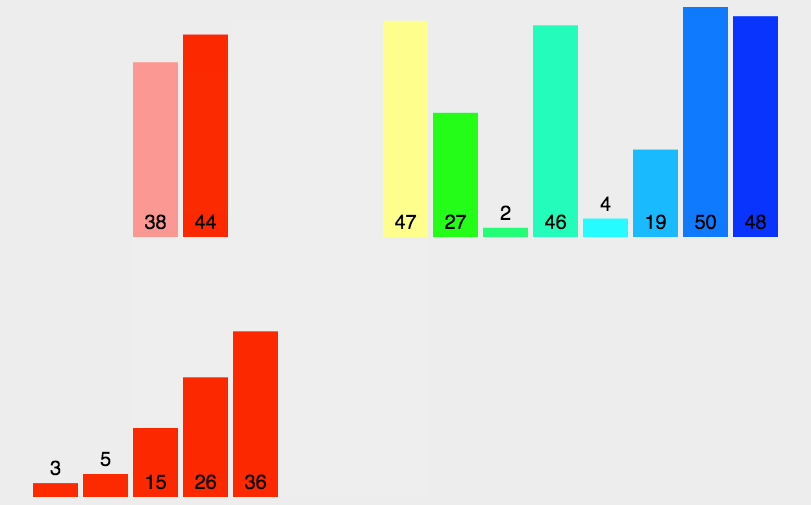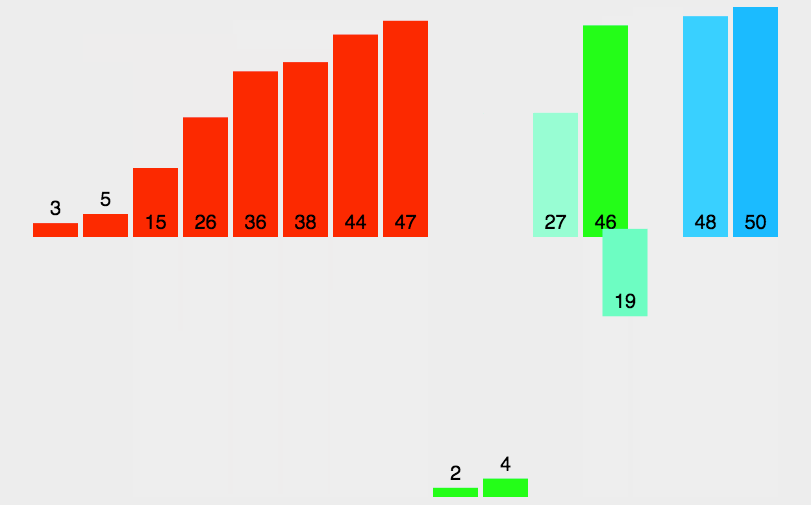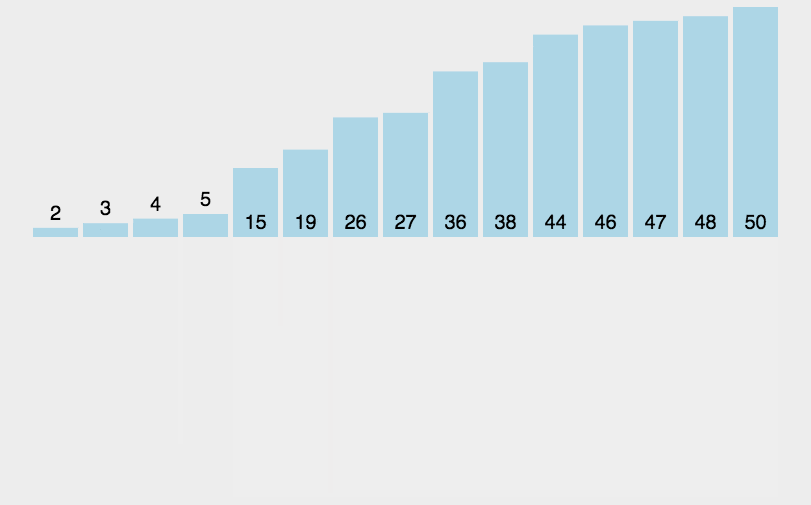
2.2 代码实现（Java）

java 复制代码

import java.util.Arrays;

public class MergeSort {
    public static void mergeSort(int[] arr) {
        if (arr == null) {
            return;
        }
        int[] temp = new int[arr.length];
        mergeSort(arr, temp, 0, arr.length - 1);
    }

    private static void mergeSort(int[] arr, int[] temp, int left, int right) {
        if (left < right) {
            int mid = left + (right - left) / 2;
            mergeSort(arr, temp, left, mid);
            mergeSort(arr, temp, mid + 1, right);
            merge(arr, temp, left, mid, right);
        }
    }

    private static void merge(int[] arr, int[] temp, int left, int mid, int right) {
        System.arraycopy(arr, left, temp, left, right - left + 1);
        int i = left;
        int j = mid + 1;
        int k = left;

        while (i <= mid && j <= right) {
            if (temp[i] <= temp[j]) {
                arr[k++] = temp[i++];
            } else {
                arr[k++] = temp[j++];
            }
        }

        while (i <= mid) {
            arr[k++] = temp[i++];
        }

        while (j <= right) {
            arr[k++] = temp[j++];
        }
    }

    public static void main(String[] args) {
        int[] arr = {8, 4, 2, 1, 7, 6, 3, 5};
        mergeSort(arr);
        System.out.println(Arrays.toString(arr));
    }
}

在上述 Java 代码中，mergeSort方法作为入口，调用递归的mergeSort方法进行分解和排序，merge方法用于合并两个有序子数组。通过临时数组temp辅助完成合并操作，保证合并过程中数据的正确处理。

2.3 性能分析

时间复杂度 ：归并排序无论在最好、最坏还是平均情况下，时间复杂度均为 O ( n log ⁡ n ) O(n \log n) O(nlogn) ，因为每次分解和合并操作的时间开销相对固定，总操作次数与 n log ⁡ n n \log n nlogn相关。

空间复杂度 ：归并排序在合并过程中需要使用额外的空间存储临时数据，空间复杂度为 O ( n ) O(n) O(n) 。

稳定性：归并排序是稳定的排序算法，在合并子数组时，相同元素的相对顺序不会发生改变。

三、堆排序（Heap Sort）

3.1 算法原理

++堆排序++利用了堆这种数据结构（大顶堆或小顶堆）的特性来实现排序。大顶堆的特点是每个父节点的值都大于或等于其子节点的值，小顶堆则相反。堆排序的主要步骤如下：

建堆：将待排序数组构建成一个大顶堆（升序排序时）或小顶堆（降序排序时）。

交换与调整：将堆顶元素（最大值或最小值）与堆的最后一个元素交换，然后对剩余元素重新调整堆结构，使其再次满足堆的性质。

重复操作：不断重复步骤 2，直到堆中只剩下一个元素，此时数组即为有序状态。

例如，对于数组[4, 6, 8, 5, 9]，先构建大顶堆[9, 6, 8, 5, 4]，然后将 9 与 4 交换，调整堆为[8, 6, 4, 5, 9]，依次类推，最终得到有序数组[4, 5, 6, 8, 9]。

3.2 代码实现（C++）

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;

// 调整堆结构
void heapify(vector<int>& arr, int n, int i) {
    int largest = i;
    int left = 2 * i + 1;
    int right = 2 * i + 2;

    if (left < n && arr[left] > arr[largest]) {
        largest = left;
    }

    if (right < n && arr[right] > arr[largest]) {
        largest = right;
    }

    if (largest != i) {
        swap(arr[i], arr[largest]);
        heapify(arr, n, largest);
    }
}

// 堆排序
void heapSort(vector<int>& arr) {
    int n = arr.size();

    // 建堆
    for (int i = n / 2 - 1; i >= 0; --i) {
        heapify(arr, n, i);
    }

    // 交换与调整
    for (int i = n - 1; i > 0; --i) {
        swap(arr[0], arr[i]);
        heapify(arr, i, 0);
    }
}

上述 C++ 代码中，heapify函数用于调整堆结构，确保以i为根节点的子树满足堆的性质。heapSort函数先进行建堆操作，然后通过不断交换堆顶元素和堆的最后一个元素，并调整堆结构，实现排序功能。

3.3 性能分析

时间复杂度 ：堆排序的时间复杂度主要由建堆和调整堆两部分组成。建堆的时间复杂度为 O ( n ) O(n) O(n) ，调整堆的时间复杂度为 O ( n log ⁡ n ) O(n \log n) O(nlogn) ，因此整体时间复杂度为 O ( n log ⁡ n ) O(n \log n) O(nlogn) ，且在最好、最坏和平均情况下均保持不变。

空间复杂度 ：堆排序在排序过程中只需要常数级别的额外空间，空间复杂度为 O ( 1 ) O(1) O(1) 。

稳定性：堆排序是不稳定的排序算法，因为在调整堆结构时，相同元素的相对顺序可能会被打乱。

四、三种高效排序算法的对比与适用场景

排序算法	平均时间复杂度	最坏时间复杂度	空间复杂度	稳定性	适用场景
快速排序	O ( n log ⁡ n ) O(n \log n) O(nlogn)	O ( n 2 ) O(n^2) O(n2)	O ( log ⁡ n ) O(\log n) O(logn)	不稳定	数据随机分布、对空间要求不高的场景；适合内部排序，常用于通用排序库
归并排序	O ( n log ⁡ n ) O(n \log n) O(nlogn)	O ( n log ⁡ n ) O(n \log n) O(nlogn)	O ( n ) O(n) O(n)	稳定	对稳定性有要求、外部排序（如处理大文件）、数据规模较大且内存充足的场景
堆排序	O ( n log ⁡ n ) O(n \log n) O(nlogn)	O ( n log ⁡ n ) O(n \log n) O(nlogn)	O ( 1 ) O(1) O(1)	不稳定	对空间要求严格、需要在线性时间内找到最大 / 最小元素的场景，如优先队列实现

总结

快速排序、归并排序和堆排序作为高效排序算法，在不同的应用场景中发挥着各自的优势。快速排序凭借其简洁高效的特点，在多数常规排序任务中表现出色；归并排序以稳定的性能和适用于外部排序的特性，成为处理大规模数据的可靠选择；堆排序则因其对空间的高效利用和稳定的时间复杂度，在特定场景下展现出独特价值。下期博客中,我将带你探索更多高级排序算法与优化技巧，例如希尔排序、计数排序等，分析它们与快速排序、归并排序、堆排序的差异，以及在不同业务场景中的实际应用案例，帮助大家进一步拓宽排序算法的知识边界。

That's all, thanks for reading!

创作不易，点赞鼓励；

知识无价，收藏备用；

持续精彩，关注不错过！