10.长度最小的子数组
(力扣209题)
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度**。**如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。示例 2:
输入:target = 4, nums = [1,4,4]
输出:1示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0使用 滑动窗口
10.1 滑动窗口
滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果
滑动窗口也可以理解为双指针法的一种,
使用一个for循环,j是滑动窗口的终止位置,i是起始位置,也是动态指针,
窗口的起始位置i:当前窗口值大于等于传入的值,i移动;
窗口的结束位置j:j就是遍历数组的指针,是for循环里的索引
代码
c++
#include <iostream>
#include <vector>
using namespace std;
// 暴力破解
class Solution1
{
public:
int minSubArrayLen(int target, vector<int> &nums)
{
int result = INT32_MAX; // 最终的结果 INT32_MAX 是一个常量,表示 32 位有符号整数的最大值。
int sum = 0; // 子序列的数值之和
int length = 0; // 子序列的长度
for (int i = 0; i < nums.size(); i++) // 字序列起点
{
sum = 0;
for (int j = i; j < nums.size(); j++) // 字序列终点
{
// 遍历的数组元素存入子序列
sum += nums[j];
if (sum >= target)
{
// 总和大于等于目标值
length = j - i + 1; // 子序列的长度
// 找符合条件最小的长度
result = length < result ? length : result;
break;
}
}
}
// result结果没有变化,没有找到
return result == INT32_MAX ? 0 : result;
}
};
class Solution
{
public:
int minSubArrayLen(int target, vector<int> &nums)
{
int result = INT32_MAX; // 最终的结果 INT32_MAX 是一个常量,表示 32 位有符号整数的最大值。
int sum = 0; // 子序列的数值之和
int length = 0; // 子序列的长度
int i = 0; // 窗口的起始位置
for (int j = 0; j < nums.size(); j++) // 遍历数组
{
// 遍历的数组元素存入子序列
sum += nums[j];
while (sum >= target)
{
// 子序列大于目标值开始位置变化 寻找最小的序列
length = j - i + 1;
result = result < length ? result : length;
sum -= nums[i++];
}
}
// 没找到 返回0
return result == INT32_MAX ? 0 : result;
}
};
int main()
{
vector<int> arr1 = {2, 3, 1, 2, 4, 3};
vector<int> arr2 = {1, 4, 4};
vector<int> arr3 = {1, 1, 1, 1, 1, 1, 1, 1};
Solution s;
cout << s.minSubArrayLen(7, arr1) << endl;
cout << s.minSubArrayLen(4, arr2) << endl;
cout << s.minSubArrayLen(11, arr3) << endl;
return 0;
}11.水果成篮
(力扣904题)
你正在探访一家农场,农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示,其中 fruits[i] 是第 i 棵树上的水果 种类 。
你想要尽可能多地收集水果。然而,农场的主人设定了一些严格的规矩,你必须按照要求采摘水果:
- 你只有 两个 篮子,并且每个篮子只能装 单一类型 的水果。每个篮子能够装的水果总量没有限制。
- 你可以选择任意一棵树开始采摘,你必须从 每棵 树(包括开始采摘的树)上 恰好摘一个水果 。采摘的水果应当符合篮子中的水果类型。每采摘一次,你将会向右移动到下一棵树,并继续采摘。
- 一旦你走到某棵树前,但水果不符合篮子的水果类型,那么就必须停止采摘。
给你一个整数数组 fruits ,返回你可以收集的水果的 最大 数目。
示例 1:
输入:fruits = [1,2,1]
输出:3
解释:可以采摘全部 3 棵树。示例 2:
输入:fruits = [0,1,2,2]
输出:3
解释:可以采摘 [1,2,2] 这三棵树。
如果从第一棵树开始采摘,则只能采摘 [0,1] 这两棵树。示例 3:
输入:fruits = [1,2,3,2,2]
输出:4
解释:可以采摘 [2,3,2,2] 这四棵树。
如果从第一棵树开始采摘,则只能采摘 [1,2] 这两棵树。示例 4:
输入:fruits = [3,3,3,1,2,1,1,2,3,3,4]
输出:5
解释:可以采摘 [1,2,1,1,2] 这五棵树。和上面的题的区别是这个是找最长子序列
- 思路
- 初始化滑动窗口的左右边界
i和j,以及一个哈希表basket来记录窗口内水果的种类和数量。 - 遍历数组,将水果加入窗口(
basket),并更新其数量。 - 当窗口内的水果种类超过两种时,收缩窗口的左边界(
i),减少对应水果的数量,直到窗口内水果种类不超过两种。 - 在每次循环中,更新最长子数组的长度(
result),即当前窗口的大小(j - i + 1)。 - 最终返回
result,即最长的满足条件的子数组长度
实例
c++
#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
// 这个是找最长的序列
class Solution
{
public:
int totalFruit(vector<int> &fruits)
{
// 收集最终水果的数目
int result = 0;
// /篮子中的水果种类数量
unordered_map<int, int> basket;
// 滑动窗口的开始位置
int i = 0;
for (int j = 0; j < fruits.size(); j++)
{
basket[fruits[j]]++;
// 篮子水果种类大于2
while(basket.size() > 2)
{
basket[fruits[i]]--;
// 如果某种水果数量为0,从篮子中移除
if( basket[fruits[i]] == 0)
{
basket.erase(fruits[i]);
}
i++;
}
result = max(result, j - i + 1);
}
return result;
}
};给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
12 螺旋矩阵
(力扣59题)
示例 1:
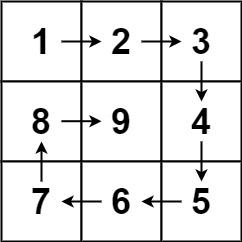
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]示例 2:
输入:n = 1
输出:[[1]]核心思路是通过逐层填充矩阵的外圈,逐步向内收缩,直到填充完整个矩阵
- 初始化一个 n ×n 的二维数组
res,所有元素初始值为 0。 - 使用变量
startx和starty表示当前层的起始位置,loop表示需要填充的圈数,offset表示当前层的边界偏移量。 - 使用一个循环逐层填充矩阵,每次循环填充当前层的上、右、下、左四条边。
- 在填充每条边时,通过
for循环依次赋值,并更新count。 - 每完成一层后,更新
startx、starty和offset,进入内层继续填充。 - 如果矩阵的维度 n 是奇数,最后单独填充矩阵中心的值。
实例
c++
// 给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,
// 且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
#include <iostream>
#include <vector>
using namespace std;
class Solution
{
public:
vector<vector<int>> generateMatrix(int n)
{
// 大小为 n×n 的二维向量,其所有元素的初始值都为 0。
vector<vector<int>> res(n, vector<int>(n, 0));
int startx = 0, starty = 0; // 数组的行列起始位置
int loop = n / 2; // 循环次数
int mid = n / 2; // 中间的值 n = 5 中间的位置就是2,2
int count = 1; // 给数组赋值
int offset = 1; // 缩进 控制的终止位置
int i, j = 0;
while (loop--)
{
i = startx;
j = starty;
// 下面开始的四个for就是模拟转了一圈
// 模拟填充上行从左到右(左闭右开)
for (j; j < n - offset; j++)
{
// 储存元素
res[i][j] = count++;
}
for (i; i < n - offset; i++)
{
// 储存元素
res[i][j] = count++;
}
for (; j > starty; j--)
{
// 储存元素
res[i][j] = count++;
}
for (; i > startx; i--)
{
// 储存元素
res[i][j] = count++;
}
// 下一圈起始位置+1 进入内圈
startx++;
starty++;
// 进入内圈偏移量+1以便同步
offset++;
}
// / 如果n为奇数的话,需要单独给矩阵最中间的位置赋值 就是count
if (n % 2) {
res[mid][mid] = count;
}
return res;
}
};
int main()
{
int n = 0;
cout << "请输入一个正整数:";
cin >> n;
Solution s1;
vector<vector<int>> res = s1.generateMatrix(n);
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
cout << res[i][j] << " ";
}
cout << endl;
}
return 0;
}