【数据结构 · 初阶】- 快速排序

目录

[一. Hoare 版本](#一. Hoare 版本)

[1. 单趟](#1. 单趟)

[2. 整体](#2. 整体)

[3. 时间复杂度](#3. 时间复杂度)

[4. 优化（抢救一下）](#4. 优化（抢救一下）)

[4.1 随机选 key](#4.1 随机选 key)

[4.2 三数取中](#4.2 三数取中)

[二. 挖坑法](#二. 挖坑法)

格式优化

[三. 前后指针（最好）](#三. 前后指针（最好）)

[四. 小区间优化](#四. 小区间优化)

[五. 改非递归](#五. 改非递归)

---

快速排序是 Hoare 提出的一种基于二叉树结构的交换排序方法。统一排升序

一. Hoare 版本

1. 单趟

目的：选出一个关键字 /关键值/基准值 key ，把他放到排好序后，最终在的位置

key 都喜欢在最左/右边，其他位置不好排

例如这样的数组：

单趟结束后要达成这样的效果：（选择，插入，冒泡排序的单趟没有这种附加效果）
此时6就在排好序后，所在的位置

---

实现：
R 往左走，找比 key 小的 ；L 往右走，找比 key 大的 ，相等无所谓**。都找到之后，交换。直至相遇**
结论：key 在左，让 R 先走，能保证相遇位置一定比 key 小。 key 在右，让 L 先走。
相遇位置既然比 key 小，就把 key 换到左边

void QuickSort(int* a, int left, int right)
{
	int begin = left, end = right;

	int keyi = left;
	while (left < right)
	{
		while (left < right && a[right] >= a[keyi]) // 右边找小
			right--; // 且要防止本来就有序，right 飘出去

		while (left < right && a[left] <= a[keyi]) // 左边找大
			left++;

		Swap(&a[left], &a[right]);
	}

	Swap(&a[keyi], &a[left]);
	keyi = left;
}

易错：
1. 不能认为外面的 while 判断过了，里面就不用判断。里面的 while 会多走几次，left 和 right 的相对位置变了，所以要再加判断。

2. 一定是 >= 否则可能出现死循环

2. 整体

递归：

上面排好单趟，被分成三段区间，[begin, keyi-1] keyi [keyi+1, end]。左右区间都无序，递归左区间。

选出 key 分成左右区间 ...... 左区间有序，递归右区间。右区间有序，整体有序
递归返回条件：区间只剩一个值或区间不存在

递归的过程虽然图上像是分出来了，其实都是在原数组上走的

和二叉树的前序很像。单趟排是处理根（key），再处理左子树（左区间），右子树（右区间）

void QuickSort(int* a, int left, int right)
{
	// 递归返回条件
	if (left >= right) // = 是只剩一个值。> 是没有值
		return;

	int begin = left, end = right;

	int keyi = left;
	while (left < right)
	{
		while (left < right && a[right] >= a[keyi]) // 右边找小
			right--; // 且要防止本来就有序，right 飘出去

		while (left < right && a[left] <= a[keyi]) // 左边找大
			left++;

		Swap(&a[left], &a[right]);
	}

	Swap(&a[keyi], &a[left]);
	keyi = left;

	// 递归 [begin, keyi-1] keyi [keyi+1, end]
	QuickSort(a, begin, keyi - 1);
	QuickSort(a, keyi + 1, end);
}

3. 时间复杂度

理想情况下：（小于）N * logN

N 个数，最终接近满二叉树 ==》logN

当 N = 100W，只需递归 20 层 N = 10亿，递归 30 层 空间消耗不大，每层减的数也不大

最终每一层 也还是 N 的量级

---

最坏：O( N^2 ) 抢救后忽略 已经顺/逆序

递归 N 层，建立 N 个栈帧，会栈溢出

4. 优化（抢救一下）

影响快排性能的是 keyi

keyi 越接近中间的位置，越二分，越接近满二叉树，深度越均匀，效率越高

不是让左边的值做 key ，而是让 key 在最左边的位置

4.1 随机选 key

（生成位置% 区间大小）+ 左边

void QuickSort(int* a, int left, int right)
{
	// 递归返回条件 ......
	int begin = left, end = right;

	// 优化1.随机选 key
	int randi = left + (rand() % (left - right));
	Swap(&a[left], &a[randi]); // 还是让最左边做 key

	int keyi = left;
	while (left < right)
	{ ...... }
}

管你有序无序，都把你变成无序

4.2 三数取中

有序 / 接近有序的情况下，选中间位置做 key 最好。但不一定是有序 / 接近有序
三数取中：选 左右中 3个位置，不是最小，也不是最大的数的位置****两两比较

int GetMidNumi(int* a, int left, int right)
{
	int mid = (left + right) / 2;
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
		{
			return mid;
		}
		else if (a[left] > a[right]) // mid 不是中间，是最大的。
		{
			return left; // 剩下两个：left 和 right 大的就是中间
		}
		else
		{
			return right;
		}
	}
	else // a[left] > a[mid]
	{
		if (a[mid] > a[right])
		{
			return mid;
		}
		else if (a[left] < a[right]) // mid 是最小的
		{
			return left; // 剩下两个：left 和 right 小的就是中间
		}
		else
		{
			return right;
		}
	}
}

// 快速排序
void QuickSort(int* a, int left, int right)
{
	// 递归返回条件 ......
	int begin = left, end = right;

	// 优化2.三数取中
	int midi = GetMidNumi(a, left, right);
	Swap(&a[midi], &a[left]);

	int keyi = left;
	while (left < right)
	{ ...... }
}

二. 挖坑法

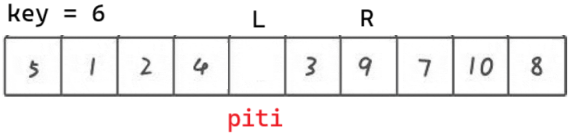
先将第一个数据存放在临时变量 key 中，形成一个坑位

piti 在左，不用想，肯定让 right 先走

right 找到比 key 小的后，把 a[right] 扔到坑里，自己变成坑。left 走。

left 找到比 key 小的后，把 a[left] 扔到坑里，自己变成坑。right 走。

重复以上过程，直到 left 和 right 相遇。相遇点一定是坑，再把 key 扔到坑里

void QuickSort2(int* a, int left, int right)
{
	// 递归返回条件
	if (left >= right)
		return;

	int begin = left, end = right;

    // 优化2.三数取中
    int midi = GetMidNumi(a, left, right);
    Swap(&a[midi], &a[left]);

	int piti = left;
	int key = a[left];
	while (left < right)
	{
		while (left < right && a[right] >= key) // 右边找小
			right--;

		a[piti] = a[right]; // 扔到左边的坑
		piti = right; // 自己成新的坑，坑到右边去了

		while (left < right && a[left] <= key) // 左边找大
			left++;

		a[piti] = a[left]; // 扔到右边的坑
		piti = left; // 自己成新的坑，坑到左边去了
	}

	a[piti] = key;

	// 递归 [begin, piti-1] piti [piti+1, end]
	QuickSort2(a, begin, piti - 1);
	QuickSort2(a, piti + 1, end);
}

格式优化

如果写单趟，上面的写法就可以

快排的递归框架是不变的，变的是单趟

// Hoare 单趟
int PartSort1(int* a, int left, int right)
{
	// 三数取中
	int midi = GetMidNumi(a, left, right);
	Swap(&a[midi], &a[left]);

	int keyi = left;
	while (left < right)
	{
		while (left < right && a[right] >= a[keyi]) // 右边找小
			right--;

		while (left < right && a[left] <= a[keyi]) // 左边找大
			left++;

		Swap(&a[left], &a[right]);
	}

	Swap(&a[keyi], &a[left]);
	keyi = left;

	return keyi;
}

// 挖坑 单趟
int PartSort2(int* a, int left, int right)
{
	// 三数取中
	int midi = GetMidNumi(a, left, right);
	Swap(&a[midi], &a[left]);

	int piti = left;
	int key = a[left];
	while (left < right)
	{
		while (left < right && a[right] >= key) // 右边找小
			right--;

		a[piti] = a[right]; // 扔到左边的坑
		piti = right; // 自己成新的坑，坑到右边去了

		while (left < right && a[left] <= key) // 左边找大
			left++;

		a[piti] = a[left]; // 扔到右边的坑
		piti = left; // 自己成新的坑，坑到左边去了
	}

	a[piti] = key;

	return piti;
}

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;

    int keyi = PartSort2(a, left, right);
	QuickSort(a, left, keyi - 1);
	QuickSort(a, keyi + 1, right);
}

三. 前后指针（最好）

1. cur 找到比 key 小的值，++prev，交换 cur 和 prev 位置的数据，++cur
2. cur 找到比 key 大的值，++cur

把比 key 大的值往右翻，比 key 小的值往左翻

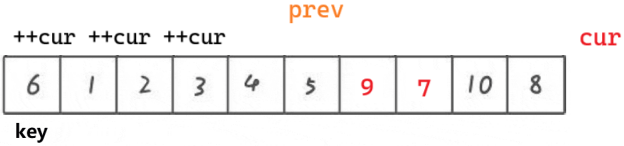
1. prev 要么紧跟着 cur（prev 下一个就是 cur）
2. prev 跟 cur 中间隔着比 key 大的一段值

int PartSort3(int* a, int left, int right)
{
	// 三数取中
	int midi = GetMidNumi(a, left, right);
	Swap(&a[midi], &a[left]);

	int keyi = left;
	int prev = left, cur = left + 1;
	while (cur <= right) // [left, right]，所以是 <=
	{
		if (a[cur] < a[keyi])
		{
			++prev;
			Swap(&a[cur], &a[prev]);
			++cur;
		}
		else
		{
			++cur;
		}
	}

	Swap(&a[prev], &a[keyi]);
	keyi = prev;

	return keyi;
}

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	int keyi = PartSort3(a, left, right);
	QuickSort(a, left, keyi - 1);
	QuickSort(a, keyi + 1, right);
}

while (cur <= right)
{
	if (a[cur] < a[keyi] && ++prev != cur)
		Swap(&a[cur], &a[prev]);

	++cur;
}

四. 小区间优化

小区间直接使用直接插入排序

希尔是当数据量特别大时，为了让大数快速往后跳才用

堆排还要建堆，很麻烦

冒泡只有教学意义，现实中几乎没用

选择排序，最好最坏都是 N^2，也没用

上面说递归图看着像二叉树

当区间特别小时，递归的次数会非常多。

光最后一层的递归数，就是总递归数的1/2。倒数第二次占1/4。倒数第三层占1/8

如果小区间直接使用直接插入排序，递归数量会少很多。现实中递归的不均匀，但怎么说也减少了50%的递归数量

void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;

	// 小区间优化 - 小区间直接使用插入排序
	if (right - left + 1 > 10) // [left, right]左闭右闭区间，要 +1
	{
		int keyi = PartSort3(a, left, right);
		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}
	else
	{
		InsertSort(a + left, right - left + 1);
	}
}

不能写成：InsertSort(a, right - left + 1)

正确。但如果是这样就出错了：

[ left , right ] 左闭右闭区间，要 +1

五. 改非递归

递归的问题：1. 效率（影响不大） 2. 递归太深，栈溢出。不能调试

递归改非递归：

**1. 直接改循环。原来正着走，递归逆着来（简单）。**eg：斐波那契数列。

2. 用栈辅助改循环。（难）eg：二叉树

递归里，实际是用下标来 分割子区间
递归里参数条件变化的是什么，栈里面存的就是什么。具体情况具体分析

---

**思路：

1. 栈里面取一段区间，单趟排序
2. 单趟分割子区间入栈
3. 子区间只有一个值、不存在时就不入栈**

为了和递归的过程一样，栈里先入右区间，再入左区间。这样就先排好左区间，再排好右区间

在栈里取单个区间时，若想先取左端点、再取右端点，就要先入右端点、再入左端点。

void QuickSortNonR(int* a, int left, int right)
{
	ST st;
	STInit(&st);
	STPush(&st, right);
	STPush(&st, left);

	while (!STEmpty(&st))
	{
		int begin = STTop(&st);
		STPop(&st);
		int end = STTop(&st);
		STPop(&st);

		int keyi = PartSort3(a, begin, end);
		// [begin,keyi-1] keyi [keyi+1, end]
		if (keyi + 1 < end)
		{
			STPush(&st, end);
			STPush(&st, keyi + 1);
		}
		if (begin < keyi - 1)
		{
			STPush(&st, keyi - 1);
			STPush(&st, begin);
		}
	}

	STDestroy(&st);
}

2 个 if 相当于递归的返回条件

本篇的分享就到这里了，感谢观看 ，如果对你有帮助，别忘了点赞+收藏+关注 。

小编会以自己学习过程中遇到的问题为素材，持续为您推送文章