三维旋转的符号问题
旋转矩阵的符号差异源于坐标系的手系规则和旋转方向定义。
首先是我们最常规的绕着z轴旋转,这是右手系下的标准定义,符合"x轴转向y轴"的正方向。
\[\mathbf{R}_z(\alpha) = \begin{pmatrix} \cos \alpha & -\sin \alpha & 0 & 0 \\ \sin \alpha & \cos \alpha & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]
这个时候,我们通常都把x轴与y轴线性变换之后所形成的角度设为\(\alpha\) ,不同角的设置就会出现不同的符号,我们通常设置角的优先度就是x>y>z,所以就有了下面不同的符号。
- X轴为基准轴:其旋转矩阵最直观,Y-Z平面完全遵循右手法则
- Y轴次之:由于Y轴旋转时Z-X平面的定义需保持坐标系一致性,导致项符号反转
- Z轴最后:作为最常用的旋转轴,其定义需兼容前两者的嵌套结果。
\[\mathbf{R}_x(\alpha) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & -\sin \alpha & 0 \\ 0 & \sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]
\[\mathbf{R}_y(\alpha) = \begin{pmatrix} \cos \alpha & 0 & \sin \alpha & 0 \\ 0 & 1 & 0 & 0 \\ -\sin \alpha & 0 & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]
欧拉角
我们把沿着每个角的旋转角度分开来表示被称之为欧拉角
!note
\(\mathbf{R}_{xyz}(\alpha, \beta, \gamma) = \mathbf{R}_x(\alpha) \, \mathbf{R}_y(\beta) \, \mathbf{R}_z(\gamma)\)
这里挖坑:可以去探究下罗德里格斯旋转公式是什么,以及怎么推导的,参考[数学]罗德里格旋转公式(Rodrigues' rotation formula) - 知乎
视图变换
相机放置的标准位置
相机本体放在(0,0,0)上,正方向为-Z方向,正上方向为+Y方向,然后场景移动,而不是相机移动
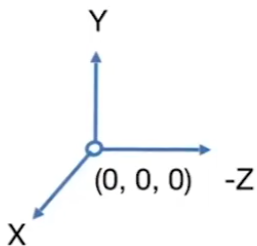
视图变换
有了这些概念之后我们就应该明白,即便我们要把相机放在世界坐标系的原点上也是世界坐标系移动,使得原点跑到了相机的坐标上,而不是移动相机跑到原点上。那么此刻我们感受到的应该是反客为主,此时相机的坐标就是原点,而世界坐标系才是需要移动的。
既然反客为主,这个时候世界坐标系的原点也不一样了,应该是相机视角下世界坐标系原点的坐标。比如,此刻相机的坐标系为(10,5,3),那么此时原点现对于相机的坐标为 (\(0-10,0-5,0-3\)) ,或者一个物品此时的坐标为(15,7,8),那么这个物品的相对坐标就为:(15-10,7-5,8-3)。
所以想要把世界坐标轴原点移动到相机就得直接减去相对坐标才行。
那么此时的变换矩阵就应该是\(T_{view} = \begin{bmatrix}1 & 0 & 0 & -x_e \\0 & 1 & 0 & -y_e \\0 & 0 & 1 & -z_e \\0 & 0 & 0 & 1\end{bmatrix}\)
当我们有了找个标准的视角之后,如果相机不是标准方向,那么就需要我们把相机的视角旋转到找个标准的位置。我们就要尝试找到找个旋转矩阵。但是这个矩阵肉眼并不好看出来,只能靠其他的办法去求了。
我们虽然不知道怎么直接拿到世界坐标系旋转到详细坐标系的旋转矩阵,但是能知道怎么把相机坐标系的点怎么在世界坐标系来表示:
\[R = \begin{bmatrix} x_{\hat{g}\times\hat{t}} & x_t & x_{-g} & 0 \\ y_{\hat{g}\times\hat{t}} & y_t & y_{-g} & 0 \\ z_{\hat{g}\times\hat{t}} & z_t & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
那么表示起来就是这样:\(p_{\text{world}} = R \cdot p_{\text{camera}}\) 这里的\(p_{\text{camera}}\) 就是相机坐标的点(基本坐标 x 倍数 = 坐标系下的坐标),那么我们要把世界坐标转换到相机坐标只需要我们用\(R^T R = R R^T = I\) 的性质对其进行转换。
我们把\(p_{\text{world}} = R \cdot p_{\text{camera}}\) 两边同时乘一个\(R^T\) 那么就出现了 \(R^T \cdot p_{\text{world}} = RR^T \cdot p_{\text{camera}}\) 最后结果就是$$R^T \cdot p_{\text{world}} = p_{\text{camera}}$$
所以旋转矩阵就是:
\[R^T=\begin{bmatrix} x_{\hat{g}\times\hat{t}} & y_{\hat{g}\times\hat{t}} & z_{\hat{g}\times\hat{t}} & 0 \\ x_t & y_t & z_t & 0 \\ x_{-g} & y_{-g} & z_{-g} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
最后再加上平移矩阵,最后的总矩阵就是:
\[\begin{bmatrix} x_{\hat{g}\times\hat{t}} & y_{\hat{g}\times\hat{t}} & z_{\hat{g}\times\hat{t}} & -x_e \\ x_t & y_t & z_t & -y_e \\ x_{-g} & y_{-g} & z_{-g} & -z_e \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
透视投影与正交投影
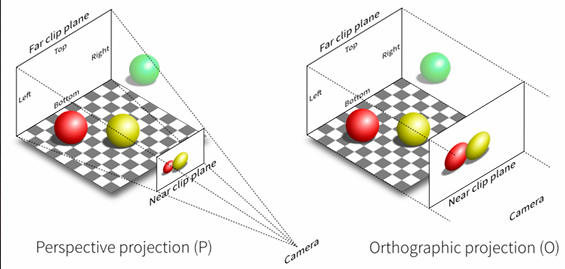
正交投影
正交投影应该没什么可说的,很直观,我们这里只看一个东西。
很多时候我们都把一个物体等价缩放到一个2x2的标准正方体里面,如图:
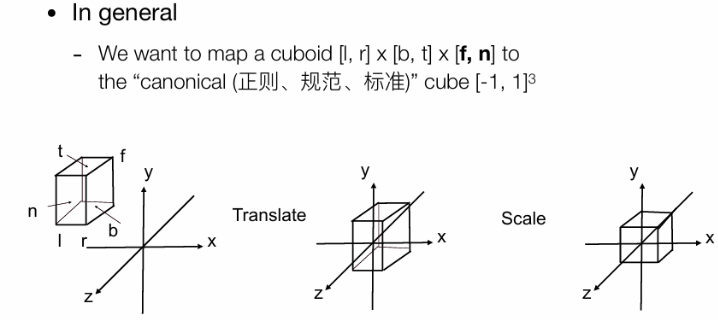
当然整个移动缩放矩阵就很清晰了
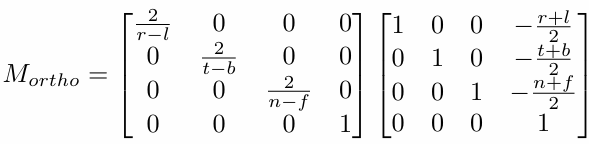
透视投影
我们重点还是透视投影。
透视投影的核心概念是远近缩放效应,即物体越远,看起来越小。
透视投影说白了就是个三角形,关系如下:
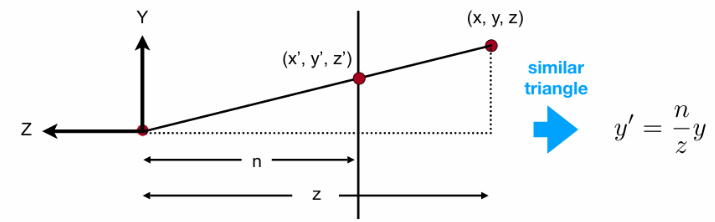
\[y' = \frac{n}{z} y, \quad x' = \frac{n}{z} x \]
其中:
- (x,y,z)是原始三维坐标
- (x′,y′)是投影后的二维坐标
- n 是近平面的位置
这个关系说明,投影后的 x′,y′值与z 反比,物体越远 (z 大),投影坐标越小。
这个时候我们希望有一个矩阵在齐次坐标能够表示到把\(\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}\) 映射为 \(\begin{pmatrix} \frac{nx}{z} \\ \frac{ny}{z} \\ \text{unknown} \\ 1 \end{pmatrix}\)
让我们一点一点地分析 :
分析:
为什么z轴的数值是unknown?
- 透视投影会改变 zz 的表现方式,在透视投影之后,我们仍然希望能够正确地表示物体的深度 z 。
- 这个公式不能简单地设为 \(\frac{n}{z} z\),因为那样会导致 z' 始终是 n,无法正确区分不同深度的物体。我们希望 z' 能保留某种线性变换形式,以便在深度缓冲(Z-buffer)等操作中使用。
变换矩阵的初步构造
为了方便计算我们将整个映射后的矩阵再乘以一个z
\[\begin{pmatrix} nx \\ ny \\ \text{still unknown} \\ z \end{pmatrix} \]
那么这个变换矩阵就应该是这样:
\[M_{\text{persp}\rightarrow\text{ortho}}\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} nx \\ ny \\ \text{still unknown} \\ z \end{pmatrix} \]
所以我们直接看都能看出来,x与y只用乘一个\(n\) ,而最后保证和z的值一样就行,所以就有了初步的结果:
\[M_{\text{persp}\rightarrow\text{ortho}}=\begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & 1 & 0 \end{pmatrix} \]
为什么最后一行为(0,0,1,0)?
我们看到 \(\begin{pmatrix} nx \\ ny \\ \text{still unknown} \\ z \end{pmatrix}\) 的最后一行实际上就是 \(\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}\) 的z。
寻找第三行的关系
其中第三个分量 ? 就是新的 z',它必须满足以下要求:
- 必须是深度的线性函数,即形如 z′=Az+B
- 在近裁剪面 z = n 时,z' 应该保持为 n,以保证近裁剪面不会被误判深度。
- 在远裁剪面 z = f 时,z' 应该保持为 f,以保证远裁剪面深度正确。
我们其实早就能发现z的值与xy的值是没有关系的,
所以前面的两个数都会是\((0,0,?,?)\)
我们知道:
!note\] **近平面上的点 (z = n) 不能变动**,即:
\[M_{\text{persp}\rightarrow\text{ortho}} \begin{pmatrix} x \\ y \\ n \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ y \\ n^2 \\ 1 \end{pmatrix} \]
这表明,第三行应该是 \((0 \ 0 \ A \ B)\) 同时满足:\(An + B = n^2\)
!note\] **远平面上的点 (z = f) 不能变动**:
\[Af + B = f^2 \]
通过解方程:
\[\begin{cases} An + B = n^2 \\ Af + B = f^2 \end{cases} \]
得到:
\[\begin{cases} A = n + f \\ B = -nf \end{cases} \]
所以,第三行最终确定为:
\[(0 \ ,0 \ ,(n+f) \ ,-nf) \]
最终的完整矩阵就为:
\[M_{\text{persp}\rightarrow\text{ortho}} = \begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{pmatrix} \]
得到了这个投影之后在做一个正交投影就能直接投射到摄像机上
最后的思考题
!note
当空间中有一个点,在frustum内,但是不在近平面与远平面上的时候,经过压缩变换之后,这个点在Z轴上的坐标,会变得离近平面更近、还是离远平面更近、还是不变?
这里的意思实际上是想让我们思考:
- 在视锥体(frustum)内部、但不在近平面或远平面上的一个点,
- 经过透视投影矩阵的压缩变换后,
- 该点的 Z 轴坐标是变得更靠近近平面,还是更靠近远平面,还是不变?
解析
这个地方我们的第一反应就应该去求 Z 轴坐标的值,这个地方实际上很好求,因为前面我们已经有了这样一个旋转矩阵了:\(\begin{pmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & n+f & -nf \\ 0 & 0 & 1 & 0 \end{pmatrix}\) 。
我们设这个frustum内一点P的齐次坐标为:\(\begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix}\)
变换后,得到新的齐次坐标:
\[M_{\text{persp} \rightarrow \text{ortho}} \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} nx \\ ny \\ (n+f)z - nf \\ z \end{pmatrix} \]
那么我们的 z' = \(\frac{(n+f)z - nf}{z} = (n+f) - \frac{nf}{z}\) ,其中 n < z < f
这个时候就很简单了,我们只需要知道这个式子的单调性就能知道整个式子随着 z' 的增大是减小还是增加,如果是前者,那么就是更靠近远平面,反之亦然。也就是说,当 z 越发靠近 n ,变换后的值也会越小,越小,那么离摄像机越近,离摄像机,那可不越靠近n吗
这里值得一提的是,这里n,f,z都是大于0的,因为在摄像机视角中,只能看见正面,后面是看不见的,也不用进行处理,所以这里的n,f,z一定都是大于0的。
这个式子不用多说,想知道单调性直接求个导就出来了:
\[\frac{d}{dz} z' = \frac{d}{dz} \left( (n+f) - \frac{nf}{z} \right) = \frac{nf}{z^2} \]
无论 z 等于何值,倒数都大于0,整个函数单调递增。
- 透视投影的本质是"压缩"远处的深度范围。
- 远离近平面的点 z 变换后会向近平面挤压,因为 透视变换非线性缩小了远处的深度范围。
- 所有在 frustum 内的点,变换后 z′ 都比原来的 z 更靠近近平面。
问题解决。