【图像处理基石】光线追踪（Ray Tracing）算法入门

在计算机图形学中，光线追踪是一种能生成超逼真图像的核心技术------小到游戏里的光影反射，大到电影特效中的全局光照，甚至是太空场景模拟（如行星表面光影、星际尘埃折射），都离不开它的支持。与传统光栅化相比，光线追踪的核心优势是物理真实性，能自然模拟阴影、反射、折射等效果，且原理直观易懂，非常适合入门学习。

本文将从「核心思想→数学基础→简化代码实现」逐步拆解，用Python写一个最小可行版光线追踪器，让你在100行代码内生成第一个光线追踪图像，真正做到"上手即能用"。

一、先搞懂：光线追踪到底在做什么？

我们肉眼看到物体，本质是「光源发出的光线照射到物体上，经过反射/折射后进入眼睛」。但直接模拟这个过程（从光源出发追踪光线）效率极低------大部分光线不会刚好进入眼睛。

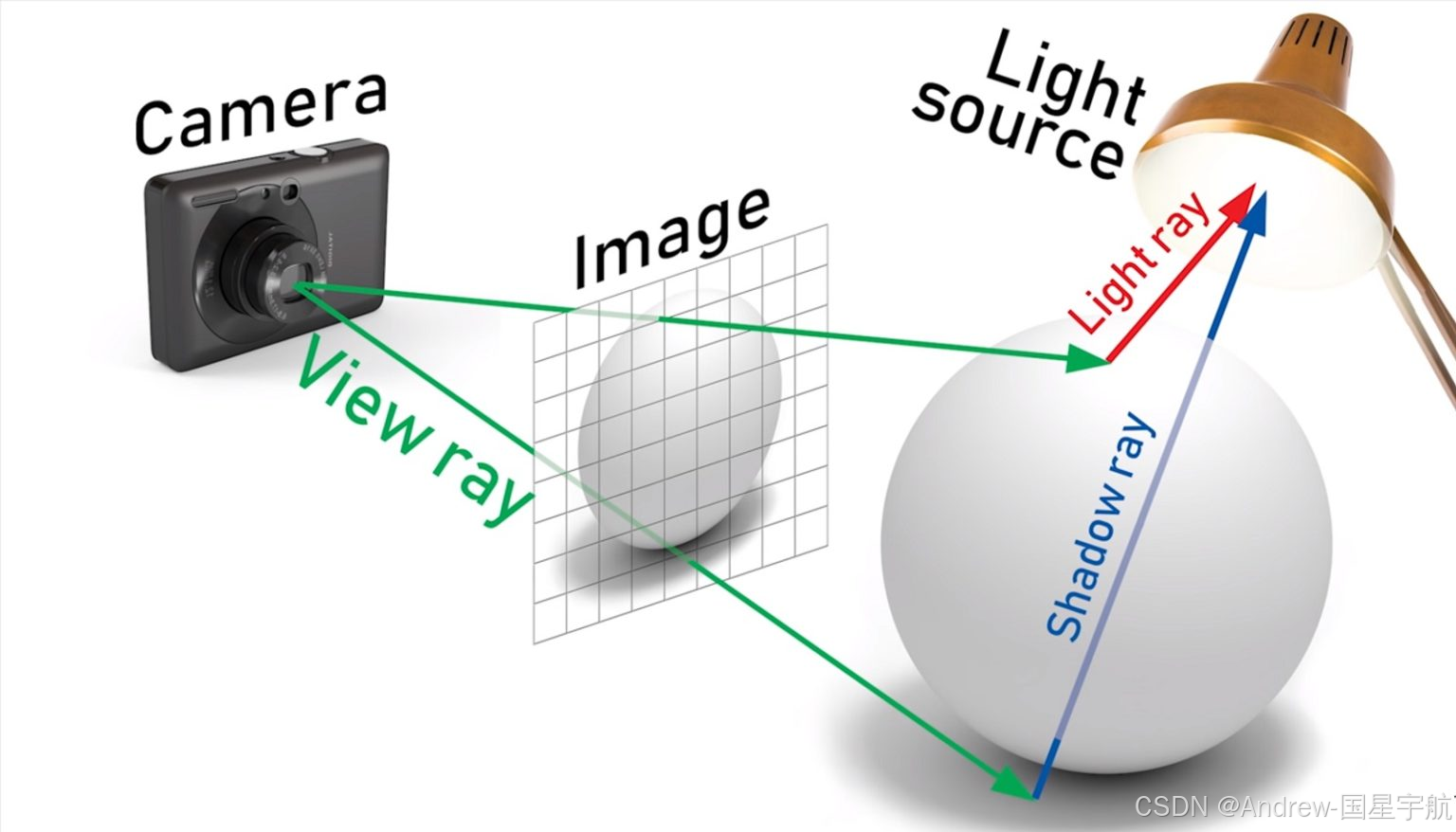
光线追踪的核心技巧是「逆向追踪」：从相机（眼睛）出发，向图像的每个像素发射一条"探测光线"，追踪这条光线是否会与场景中的物体相交；如果相交，就计算该点的颜色（结合光源、材质），最终将颜色填充到对应像素。

这个过程可以类比为"用探照灯照场景"：

1. 探照灯（相机）向像素发射一束光；
2. 光线碰到物体（如球体）就"反弹"，并检查是否能直接看到光源（判断是否在阴影中）；
3. 根据物体材质（如漫反射、镜面反射）计算该点的最终颜色；
4. 重复这个过程，直到所有像素都被填充。

光线追踪 vs 光栅化（快速对比）

特性	光栅化（传统游戏常用）	光线追踪
核心逻辑	直接将3D物体投影到2D平面	逆向追踪光线与物体的交互
光影效果	需额外实现阴影、反射（效果较假）	自然支持阴影、反射、折射
性能	速度快（实时渲染）	速度慢（需离线渲染，可通过GPU/集群加速）
适用场景	游戏、实时交互	电影特效、静态渲染、高精度模拟

对入门者来说，光线追踪的优势是"逻辑简单+效果惊艳"，不需要复杂的矩阵变换（光栅化的痛点），只需掌握基础的几何计算即可。

二、核心数学基础（极简版，够用就好）

实现光线追踪只需要3个核心数学工具，无需深入推导，直接用公式即可：

1. 光线的数学表达

光线可以看作「从起点出发，沿某个方向无限延伸的直线」，用参数方程表示为：
r⃗(t)=O⃗+t⋅D⃗ \vec{r}(t) = \vec{O} + t \cdot \vec{D} r (t)=O +t⋅D

• O⃗\vec{O}O ：光线起点（相机位置）；
• D⃗\vec{D}D ：光线方向向量（单位向量，长度=1）；
• ttt：参数（t>0t>0t>0，表示光线传播的距离）。

2. 光线与物体的交点计算（以球体为例）

场景中最容易计算交点的物体是球体（复杂物体可由球体组合而成）。球体的方程为：
(P⃗−C⃗)⋅(P⃗−C⃗)=R2 (\vec{P} - \vec{C}) \cdot (\vec{P} - \vec{C}) = R^2 (P −C )⋅(P −C )=R2

• C⃗\vec{C}C ：球心坐标；
• RRR：球体半径；
• P⃗\vec{P}P ：球面上任意一点。

将光线方程代入球体方程，可推导出一个二次方程 at2+bt+c=0at^2 + bt + c = 0at2+bt+c=0，求解 ttt 即可得到交点：

• a=D⃗⋅D⃗a = \vec{D} \cdot \vec{D}a=D ⋅D （因 D⃗\vec{D}D 是单位向量，a=1a=1a=1，可简化计算）；
• b=2⋅(D⃗⋅(O⃗−C⃗))b = 2 \cdot (\vec{D} \cdot (\vec{O} - \vec{C}))b=2⋅(D ⋅(O −C ))；
• c=(O⃗−C⃗)⋅(O⃗−C⃗)−R2c = (\vec{O} - \vec{C}) \cdot (\vec{O} - \vec{C}) - R^2c=(O −C )⋅(O −C )−R2；
• 判别式 Δ=b2−4ac\Delta = b^2 - 4acΔ=b2−4ac：
  • Δ<0\Delta < 0Δ<0：无交点（光线没碰到球体）；
  • Δ=0\Delta = 0Δ=0：光线与球体相切（1个交点）；
  • Δ>0\Delta > 0Δ>0：光线穿过球体（2个交点，取 ttt 最小的那个，即最近的交点）。

3. 颜色计算（漫反射模型）

物体的颜色由「光源照射+材质反射」决定，我们先实现最简单的Lambert漫反射模型 （适合模拟粗糙表面，如墙面、地面）：
color=材质颜色×光源颜色×max⁡(0,N⃗⋅L⃗) color = 材质颜色 \times 光源颜色 \times \max(0, \vec{N} \cdot \vec{L}) color=材质颜色×光源颜色×max(0,N ⋅L )

• N⃗\vec{N}N ：交点处的物体法向量（球体的法向量=交点-球心，归一化后）；
• L⃗\vec{L}L ：交点指向光源的单位向量；
• max⁡(0,N⃗⋅L⃗)\max(0, \vec{N} \cdot \vec{L})max(0,N ⋅L )：保证只有光线照射到的面才会发光（法向量与光线方向夹角≤90°）。

三、Python代码实现：100行生成第一个光线追踪图

我们用Python的PIL库（处理图像）和numpy（向量计算）实现一个简化版光线追踪器，功能包括：

• 场景：1个光源 + 3个球体；
• 效果：漫反射 + 阴影；
• 输出：200x200的图像文件。

第一步：安装依赖

pip install pillow numpy

第二步：完整代码（注释详细，可直接运行）

import numpy as np
from PIL import Image

# -------------------------- 1. 基础工具函数（向量计算）--------------------------
def normalize(v):
    """向量归一化（转为单位向量）"""
    return v / np.linalg.norm(v)

def dot(v1, v2):
    """向量点积"""
    return np.dot(v1, v2)

def subtract(v1, v2):
    """向量减法"""
    return v1 - v2

# -------------------------- 2. 场景定义（球体+光源）--------------------------
class Sphere:
    def __init__(self, center, radius, color, specular=500):
        self.center = np.array(center, dtype=np.float32)  # 球心坐标 (x,y,z)
        self.radius = radius  # 半径
        self.color = np.array(color, dtype=np.float32)  # 颜色 (R,G,B)，0-255
        self.specular = specular  # 镜面反射系数（越大越亮）

class Light:
    def __init__(self, position, intensity):
        self.position = np.array(position, dtype=np.float32)  # 光源位置
        self.intensity = intensity  # 光强（0-255）

# 场景初始化：3个球体 + 1个点光源
scene = [
    Sphere(center=(0, -1, 3), radius=1, color=(255, 0, 0)),    # 红色球体
    Sphere(center=(2, 0, 4), radius=1, color=(0, 255, 0)),    # 绿色球体
    Sphere(center=(-2, 0, 4), radius=1, color=(0, 0, 255)),   # 蓝色球体
    Sphere(center=(0, -5001, 0), radius=5000, color=(255, 255, 255))  # 白色地面（超大球体）
]
light = Light(position=(5, 5, -10), intensity=255)

# -------------------------- 3. 光线与球体交点检测 --------------------------
def intersect_ray_sphere(ray_origin, ray_dir, sphere):
    """
    计算光线与球体的交点
    返回：t（光线到交点的距离），若无交点返回None
    """
    oc = subtract(ray_origin, sphere.center)  # O - C
    a = dot(ray_dir, ray_dir)  # 单位向量点积=1，可简化为1
    b = 2 * dot(oc, ray_dir)
    c = dot(oc, oc) - sphere.radius ** 2
    delta = b ** 2 - 4 * a * c  # 判别式

    if delta < 0:
        return None  # 无交点
    # 取最近的交点（t>0）
    t1 = (-b - np.sqrt(delta)) / (2 * a)
    t2 = (-b + np.sqrt(delta)) / (2 * a)
    return t1 if t1 > 0 else t2

# -------------------------- 4. 计算像素颜色 --------------------------
def trace_ray(ray_origin, ray_dir, scene, light, depth=0):
    """
    追踪一条光线，返回该光线对应的颜色
    depth：递归深度（用于反射/折射，本文简化为0）
    """
    # 1. 找到光线与场景中最近的物体
    closest_t = float('inf')
    closest_sphere = None
    for sphere in scene:
        t = intersect_ray_sphere(ray_origin, ray_dir, sphere)
        if t and t < closest_t:
            closest_t = t
            closest_sphere = sphere

    # 2. 无交点：返回黑色（背景）
    if closest_sphere is None:
        return np.array([0, 0, 0], dtype=np.uint8)

    # 3. 计算交点坐标和法向量
    hit_point = ray_origin + closest_t * ray_dir  # 交点 P = O + t*D
    normal = normalize(subtract(hit_point, closest_sphere.center))  # 法向量 N = (P - C)归一化

    # 4. 计算漫反射颜色（Lambert模型）
    light_dir = normalize(subtract(light.position, hit_point))  # 光线方向 L = (光源 - 交点)归一化
    diffuse_intensity = max(0, dot(normal, light_dir))  # 漫反射强度
    diffuse_color = closest_sphere.color * diffuse_intensity * (light.intensity / 255)

    # 5. 计算阴影（判断交点是否被其他物体遮挡）
    shadow_ray_origin = hit_point + 1e-3 * normal  # 阴影光线起点（避免自遮挡）
    shadow_ray_dir = light_dir
    shadow_closest_t = intersect_ray_sphere(shadow_ray_origin, shadow_ray_dir, closest_sphere)
    for sphere in scene:
        if sphere == closest_sphere:
            continue
        t = intersect_ray_sphere(shadow_ray_origin, shadow_ray_dir, sphere)
        if t and t < closest_t:
            # 有遮挡：阴影区域，颜色减半
            diffuse_color *= 0.5
            break

    # 6. 限制颜色范围在0-255
    return np.clip(diffuse_color, 0, 255).astype(np.uint8)

# -------------------------- 5. 主渲染函数 --------------------------
def render(scene, light, width=200, height=200):
    """
    渲染场景：为每个像素发射光线，计算颜色
    width/height：图像分辨率
    """
    # 相机参数（简化：相机在原点，看向z轴正方向）
    camera_origin = np.array([0, 0, 0], dtype=np.float32)
    fov = np.pi / 3  # 视场角（60度）
    aspect_ratio = width / height  # 宽高比

    # 创建图像画布
    image = Image.new("RGB", (width, height))
    pixels = image.load()

    # 遍历每个像素
    for y in range(height):
        for x in range(width):
            # 1. 将像素坐标转为标准化设备坐标（NDC）：[-1,1]
            ndc_x = (x / width) * 2 - 1  # x: 0→width → -1→1
            ndc_y = 1 - (y / height) * 2  # y: 0→height → 1→-1（翻转y轴）

            # 2. 转为相机空间光线方向（考虑视场角和宽高比）
            ray_dir_x = ndc_x * aspect_ratio * np.tan(fov / 2)
            ray_dir_y = ndc_y * np.tan(fov / 2)
            ray_dir_z = 1  # 相机看向z轴正方向
            ray_dir = normalize(np.array([ray_dir_x, ray_dir_y, ray_dir_z]))

            # 3. 追踪光线，获取颜色
            color = trace_ray(camera_origin, ray_dir, scene, light)

            # 4. 填充像素
            pixels[x, y] = tuple(color)

    # 保存图像
    image.save("ray_tracing_result.png")
    print("渲染完成！图像已保存为 ray_tracing_result.png")

# -------------------------- 运行渲染 --------------------------
if __name__ == "__main__":
    render(scene, light)

第三步：运行结果

代码运行后会生成 ray_tracing_result.png，效果如下（200x200分辨率）：

• 三个彩色球体（红、绿、蓝）落在白色地面上；
• 每个球体都有自然的阴影（被其他球体或地面遮挡）；
• 球体表面的亮度随光线角度变化（漫反射效果）。

如果你的运行结果是黑色，检查以下几点：

1. 球体坐标和半径是否正确（避免光线没击中物体）；
2. 光源位置是否合理（本文光源在(5,5,-10)，从侧后方照射）；
3. numpy 和 pillow 版本是否兼容（建议用Python 3.8+）。

四、入门后如何进阶？

本文实现的是「最小可行版光线追踪器」，仅包含漫反射和阴影。要实现更逼真的效果，可以逐步添加以下功能：

1. 基础进阶（1-2天可完成）

• 镜面反射 ：在trace_ray中添加递归，计算反射光线（反射向量公式：R⃗=2(N⃗⋅L⃗)N⃗−L⃗\vec{R} = 2(\vec{N} \cdot \vec{L})\vec{N} - \vec{L}R =2(N ⋅L )N −L ）；
• 抗锯齿（Supersampling）：每个像素发射多条光线（如4x4），取颜色平均值，解决锯齿边缘；
• 多光源支持 ：修改trace_ray，遍历多个光源计算总光照。

2. 中级进阶（1周可完成）

• 折射效果：添加透明材质（如玻璃球），用斯涅尔定律计算折射光线；
• 纹理映射：给球体贴纹理图片（用球坐标映射纹理像素）；
• 并行加速 ：用multiprocessing或numba加速渲染（Python单线程渲染200x200需几秒，并行后可提速10倍）。

3. 高级方向（结合高性能计算）

• GPU加速：用CUDA（Python+PyTorch/CuPy）重写代码，渲染1080P图像；
• 路径追踪（Path Tracing）：用蒙特卡洛方法模拟全局光照（更逼真的间接照明）；
• 太空场景适配：模拟行星表面的漫反射+镜面反射（如月球的灰阶材质、木星的气态纹理），添加星空背景（随机生成远距离光点）。

五、核心总结

光线追踪的本质的是「逆向追踪光线+几何交点计算+物理着色」，其入门门槛远低于想象------只要掌握"向量点积、归一化"两个核心数学工具，就能实现基础效果。

本文的Python代码虽然简化了很多细节（如无反射、无折射），但完整保留了光线追踪的核心流程：相机发射光线→检测交点→计算光照→填充像素。你可以在此基础上逐步迭代，最终实现支持复杂材质和全局光照的渲染器。

如果在扩展过程中遇到问题（如反射递归栈溢出、折射方向计算错误），欢迎在评论区交流～ 后续会更新"光线追踪+GPU加速""路径追踪实现"等进阶内容，敬请关注！