【CF】Day69——⭐Codeforces Round 897 (Div. 2) D (图论 | 思维 | DFS

D. Cyclic Operations

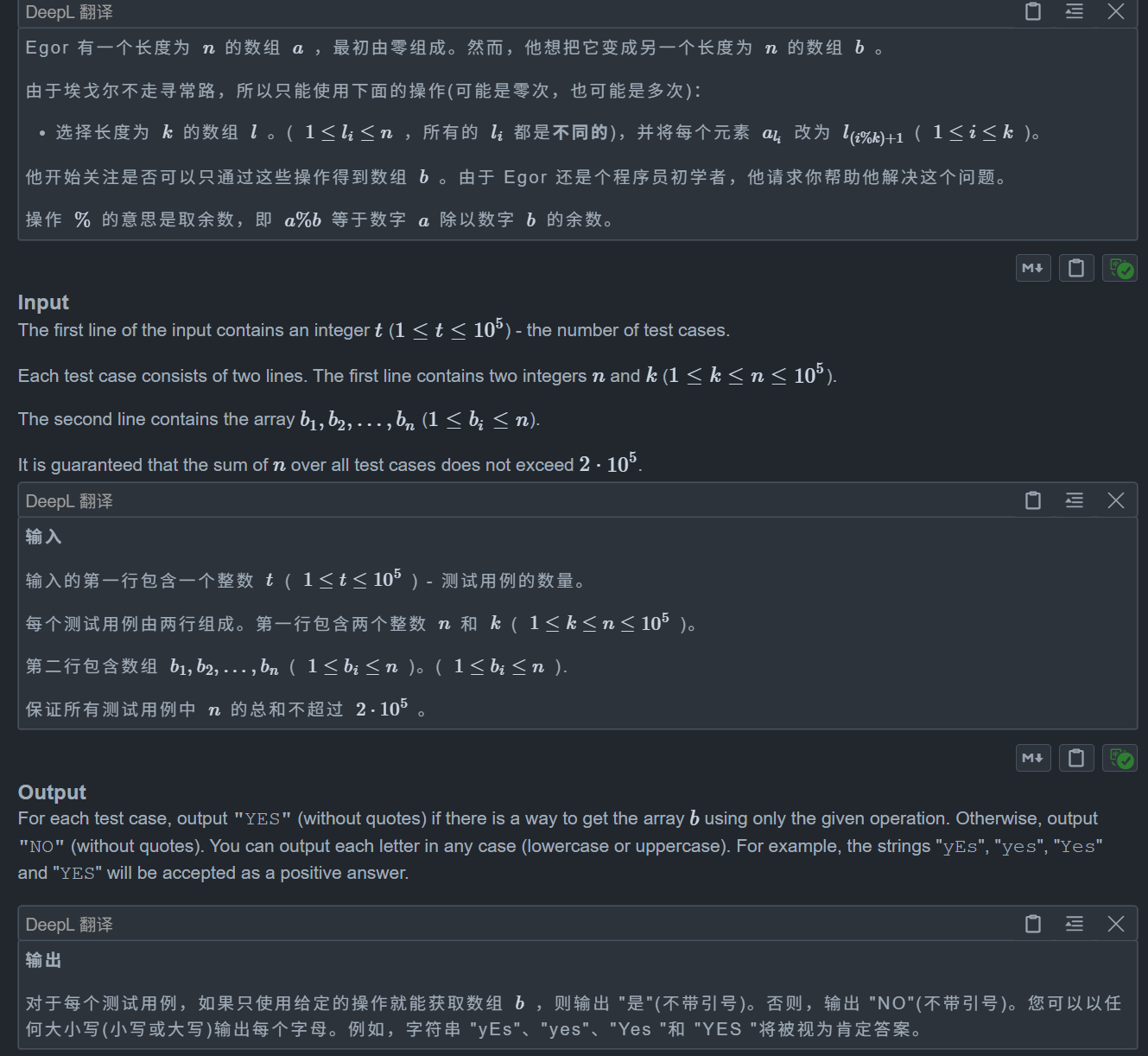
题目：

思路：

非常好的一题

对于这题我们要学会转换和提取条件，从特殊到一般

我们可以考虑特殊情况先，即 k = n 和 k = 1时，对于 k = 1，我们可以显然发现必须满足 b $i$ = i，而对于 k = n 时，我们可以发现一个特点，比如对于 2 3 1 这个例子，我们可以一个一个构造，对于 2，我们肯定是构造一个 1 2 这样的结构，对于 3 那就是 2 3，对于 1，那就是 3 1，所以最后的 l 可以是 1 2 3

我们试着进一步讨论，可以发现其实这样的一个结构：第 i 个节点指向第 b $i$ 个节点

比如 2 3 1，即 1 要指向 2，2要指向 3，3要指向 1，最后形成一个图：1 -> 2 -> 3 -> 1，我们发现这其实就是一个环，并且长度为 n，我们试着扩展一下

对于 2 3 5 3 4，我们假设 k = 3，那么对于前三个我们可以这样构造 l = 1 2 3，构造完后就是 2 3 1 0 0，对于后三个我们这样构造 l = 3 5 4，这样最后就是 2 3 5 3 4了，我们来看看这个答案是否也存在环，构建图：1->2->3->5->4->3 我们发现存在 3 5 4 这个环，并且我们还可以发现其长度恰好也为 k

所以我们可以猜测一个结论：最后构造出来的图如果有环则环的长度一定为 k

显然这时可行的，为什么呢？由于我们每次选取 k 个数构造的时候都是先构造一个环，而下次的构造如果和之前的环有交集那么就一定会断边来构造一个新环，所以最后一个连通分量里面只有一个环，且这个环的长度一定得是 k，所以我们就可以按照结论模拟即可

代码：

cpp 复制代码

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"

void solve()
{
    int n, k;
    cin >> n >> k;
    vector<int> b(n+1),vis(n+1,0);
    for (int i = 1; i <= n; i++)
    {
        cin >> b[i];
    }
    if (k == 1)
    {
        for (int i = 1; i <= n; i++)
        {
            if (b[i] != i)
            {
                no;
                return;
            }
        }
        yes;
        return;
    }
    for (int i = 1; i <= n; i++)
    {
        if (vis[i])
            continue;
        int fa = i;
        while (!vis[fa])
        {
            vis[fa] = i;
            fa = b[fa];
        }
        if (vis[fa] == i)
        {
            int son = fa;
            int len = 0;
            do
            {
                len++;
                son = b[son];
            } while (son != fa);
            if (len != k)
            {
                no;
                return;
            }
        }
    }
    yes;
}

signed main()
{
    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

【CF】Day69——⭐Codeforces Round 897 (Div. 2) D (图论 | 思维 | DFS | 环)

D. Cyclic Operations

题目：

思路：

代码：