本项目代码在个人github链接:https://github.com/KLWU07/Machine-learning-Project-practice
六种分类算法分别为逻辑回归LR、线性判别分析LDA、K近邻KNN、决策树CART、朴素贝叶斯NB、支持向量机SVM。
一、项目代码描述
1.数据准备和分析可视化
加载鸢尾花数据集,并指定列名。数据集包含4个特征(花萼长度、花萼宽度、花瓣长度、花瓣宽度)和1个类别标签。数据维度: 行 150,列 5。
(1)统计描述:样本数量分布、可视化。
| sepal-length | sepal-width | petal-length | petal-width | |
|---|---|---|---|---|
| count | 150.000000 | 150.000000 | 150.000000 | 150.000000 |
| mean | 5.843333 | 3.054000 | 3.758667 | 1.198667 |
| std | 0.828066 | 0.433594 | 1.764420 | 0.763161 |
| min | 4.300000 | 2.000000 | 1.000000 | 0.100000 |
| 25% | 5.100000 | 2.800000 | 1.600000 | 0.300000 |
| 50% | 5.800000 | 3.000000 | 4.350000 | 1.300000 |
| 75% | 6.400000 | 3.300000 | 5.100000 | 1.800000 |
| max | 7.900000 | 4.400000 | 6.900000 | 2.500000 |
(2)箱线图:展示各特征的分布和离群值。

(3)直方图:展示各特征的分布情况。

(4)散点矩阵图:展示特征间两两关系。

2.数据预处理和模型比较
(1)数据预处理
这里清理数据后,不用处理缺失值和异常值检测。接下来特征和目标变量 选择X、Y;数据集划分 训练集、测试集;数据标准化 ;固定随机种子确保结果可重复。
(2)算法比较
初始化6种分类算法:逻辑回归、线性判别分析、K近邻、决策树、朴素贝叶斯、支持向量机。
使用10折交叉验证评估每个算法(这里对比了选用5折和8折结果没10折好);
打印各算法的平均准确率和标准差、箱线图比较各算法性能、包含训练时间记录和特征重要性分析。

bash
模型训练及交叉验证结果:
LR: 准确率 0.9667 (±0.0167) | 训练时间: 0.0640s
LDA: 准确率 0.9750 (±0.0204) | 训练时间: 0.0399s
KNN: 准确率 0.9750 (±0.0204) | 训练时间: 0.0239s
CART: 准确率 0.9750 (±0.0204) | 训练时间: 0.0190s
NB: 准确率 0.9750 (±0.0204) | 训练时间: 0.0190s
SVM: 准确率 0.9750 (±0.0204) | 训练时间: 0.0408s3.模型评估
在验证集上预测输出准确率、混淆矩阵、分类报告(精确率、召回率、F1值等)。最佳模型 线性判别分析LDA
(1)混淆矩阵:行表示真实类别(Actual Class),列表示预测类别(Predicted Class)。
(2)分类报告:
Precision (精确率):模型预测为该类的样本中,真实是该类的比例。
Recall (召回率)真实是该类的样本中,被模型正确找出的比例。
F1-Score:精确率和召回率的调和平均数,综合衡量模型性能。
bash
测试集性能:
LR 准确率: 0.8667 ############################################ 1
LR 模型详细评估:
混淆矩阵:
[[ 7 0 0]
[ 0 10 2]
[ 0 2 9]]
分类报告:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 7
Iris-versicolor 0.83 0.83 0.83 12
Iris-virginica 0.82 0.82 0.82 11
accuracy 0.87 30
macro avg 0.88 0.88 0.88 30
weighted avg 0.87 0.87 0.87 30
LDA 准确率: 0.9667 ############################################ 2
LDA 模型详细评估:
混淆矩阵:
[[ 7 0 0]
[ 0 11 1]
[ 0 0 11]]
分类报告:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 7
Iris-versicolor 1.00 0.92 0.96 12
Iris-virginica 0.92 1.00 0.96 11
accuracy 0.97 30
macro avg 0.97 0.97 0.97 30
weighted avg 0.97 0.97 0.97 30
KNN 准确率: 0.8667 ############################################ 3
CART 准确率: 0.9000 ############################################ 4
NB 准确率: 0.8333 ############################################ 5
SVM 准确率: 0.8667 ############################################ 6
SVM 模型详细评估:
混淆矩阵:
[[ 7 0 0]
[ 0 10 2]
[ 0 2 9]]
分类报告:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 7
Iris-versicolor 0.83 0.83 0.83 12
Iris-virginica 0.82 0.82 0.82 11
accuracy 0.87 30
macro avg 0.88 0.88 0.88 30
weighted avg 0.87 0.87 0.87 304.两种特征重要性分析
(1)决策树的Gini重要性
(2)LDA的系数绝对值

最好模型
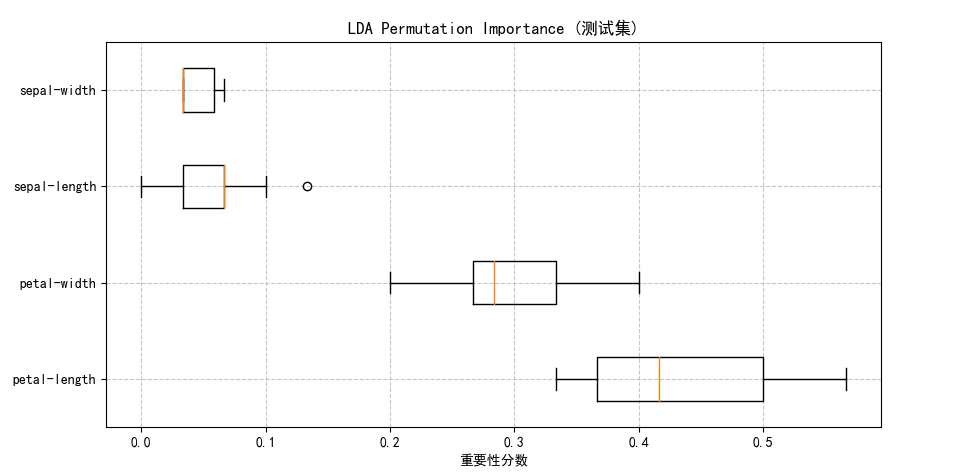
二、完整代码(每行注释)
python
# 导入必要的库
import numpy as np # 数值计算库
import matplotlib.pyplot as plt # 绘图库
from pandas import read_csv # 数据读取
from pandas.plotting import scatter_matrix # 散点矩阵图
from sklearn.model_selection import train_test_split, cross_val_score, StratifiedKFold # 数据分割和交叉验证
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score # 评估指标
from sklearn.linear_model import LogisticRegression # 逻辑回归
from sklearn.tree import DecisionTreeClassifier # 决策树
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis # 线性判别分析
from sklearn.neighbors import KNeighborsClassifier # K近邻
from sklearn.naive_bayes import GaussianNB # 高斯朴素贝叶斯
from sklearn.svm import SVC # 支持向量机
from sklearn.preprocessing import StandardScaler # 数据标准化
from sklearn.inspection import permutation_importance # 特征重要性评估
from time import time # 计时功能
from matplotlib import rcParams # matplotlib配置
# 设置中文字体和负号显示
rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei'] # 使用黑体和微软雅黑
rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 数据加载部分
filename = 'iris.data.csv' # 数据集文件名
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class'] # 定义列名
dataset = read_csv(filename, names=names) # 读取CSV文件
# 数据探索
print('数据维度: 行 %s,列 %s' % dataset.shape) # 打印数据形状
print(dataset.head(10)) # 查看前10行数据
print(dataset.describe()) # 统计描述信息
print(dataset.groupby('class').size()) # 查看类别分布
# 数据可视化
# 箱线图:展示数据分布和离群值
dataset.plot(kind='box', subplots=True, layout=(2, 2), sharex=False, sharey=False)
plt.suptitle('各特征箱线图') # 设置主标题
plt.show()
# 直方图:展示数据分布
dataset.hist()
plt.suptitle('各特征分布直方图')
plt.show()
# 散点矩阵图:展示特征间关系
scatter_matrix(dataset)
plt.suptitle('特征间散点矩阵图')
plt.show()
# 数据预处理
array = dataset.values # 转换为numpy数组
X = array[:, 0:4] # 特征矩阵(前4列)
Y = array[:, 4] # 目标变量(第5列)
validation_size = 0.2 # 测试集比例
seed = 7 # 随机种子
# 分割训练集和测试集(80%训练,20%测试)
X_train, X_validation, Y_train, Y_validation = train_test_split(
X, Y, test_size=validation_size, random_state=seed)
# 数据标准化(Z-score标准化)
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train) # 拟合训练集并转换
X_validation = scaler.transform(X_validation) # 用训练集的参数转换测试集
# 模型配置
models = {
'LR': LogisticRegression(max_iter=1000, multi_class='multinomial', solver='lbfgs', random_state=seed),
'LDA': LinearDiscriminantAnalysis(), # 线性判别分析
'KNN': KNeighborsClassifier(), # K近邻
'CART': DecisionTreeClassifier(random_state=seed), # 决策树
'NB': GaussianNB(), # 朴素贝叶斯
'SVM': SVC(C=1.0, kernel='rbf', gamma='scale', probability=True, random_state=seed) # 支持向量机
}
# 模型训练与评估
print("\n模型训练及交叉验证结果:")
results = [] # 存储各模型结果
for key in models:
start = time() # 开始计时
# 10折分层交叉验证(保持类别比例)
kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=seed)
cv_results = cross_val_score(models[key], X_train, Y_train, cv=kfold, scoring='accuracy')
# 训练模型
models[key].fit(X_train, Y_train)
train_time = time() - start # 计算训练时间
results.append(cv_results) # 保存交叉验证结果
# 打印模型性能
print(f'{key}: 准确率 {cv_results.mean():.4f} (±{cv_results.std():.4f}) | 训练时间: {train_time:.4f}s')
# 算法比较箱线图
plt.figure(figsize=(10, 6))
plt.boxplot(results, labels=models.keys()) # 绘制箱线图
plt.title('算法性能比较 (10折交叉验证)')
plt.ylabel('准确率')
plt.grid(True, linestyle='--', alpha=0.7) # 添加网格线
plt.show()
# 测试集评估
print("\n测试集性能:")
best_model = None # 记录最佳模型
best_acc = 0 # 记录最高准确率
for name, model in models.items():
y_pred = model.predict(X_validation) # 预测测试集
acc = accuracy_score(Y_validation, y_pred) # 计算准确率
print(f"{name} 准确率: {acc:.4f}")
# 更新最佳模型
if acc > best_acc:
best_acc = acc
best_model = name
# 打印最佳模型或SVM的详细评估
if name == best_model or name == 'SVM':
print(f"\n{name} 模型详细评估:")
print("混淆矩阵:\n", confusion_matrix(Y_validation, y_pred)) # 混淆矩阵
print("分类报告:\n", classification_report(Y_validation, y_pred)) # 分类报告
# 特征重要性分析
plt.figure(figsize=(12, 5))
# 决策树特征重要性
plt.subplot(1, 2, 1)
importances = models['CART'].feature_importances_ # 获取重要性分数
indices = np.argsort(importances)[::-1] # 按重要性排序
plt.bar(range(X.shape[1]), importances[indices], color='#1f77b4') # 绘制条形图
plt.xticks(range(X.shape[1]), np.array(names)[indices], rotation=45) # 设置x轴标签
plt.title('决策树 (CART) 特征重要性')
plt.ylabel('Gini Importance') # Gini重要性
# LDA特征系数
plt.subplot(1, 2, 2)
coef = np.mean(np.abs(models['LDA'].coef_), axis=0) # 取系数绝对值平均
indices = np.argsort(coef)[::-1] # 排序
plt.bar(range(X.shape[1]), coef[indices], color='#ff7f0e')
plt.xticks(range(X.shape[1]), np.array(names)[indices], rotation=45)
plt.title('LDA 特征系数绝对值')
plt.ylabel('系数绝对值')
plt.tight_layout() # 自动调整子图间距
plt.show()
# Permutation Importance(排列重要性)
print(f"\n最佳模型 '{best_model}' 的Permutation Importance:")
# 计算特征重要性(通过打乱特征值观察准确率变化)
result = permutation_importance(models[best_model], X_validation, Y_validation,
n_repeats=10, random_state=seed)
sorted_idx = result.importances_mean.argsort()[::-1] # 按重要性排序
# 绘制重要性箱线图
plt.figure(figsize=(10, 5))
plt.boxplot(result.importances[sorted_idx].T,
vert=False, labels=np.array(names)[sorted_idx])
plt.title(f"{best_model} Permutation Importance (测试集)")
plt.xlabel('重要性分数')
plt.grid(True, linestyle='--', alpha=0.7)
plt.show()