一.行列式
1.定义和性质
(1)第一种定义
例如:二阶行列式,其结果是以这里两个向量为邻边的平行四边形的面积(三阶行列式也就是体积)
总结:n阶行列式是由这n个向量组成的,其结果为这n个向量为邻边的n维图形的体积
(2)性质
- 行列互换,其值不变
- 若行列式的某一行为0则,行列式的值为0
- 若行列式的某一行有公因子,可提出行列式外
- 行列式中的某一行的元素均是两个数之和,则可拆成两个行列式之和
- 互换两行或两列,行列式变号
- 若行列式的某两行对应成比例,行列式的值为0
- 把行列式的某一行的k倍加到另一行,行列式的值不变
(3)第二种定义
逆序:大数排在小数的前面
逆序数:一个排列中的逆序总数
奇排列和偶排列:逆序数为奇数位奇排列,反之为偶排列
-1上面的r(一堆)就是逆序数

(4)第三种定义
余子式:在n阶行列式中去掉所选的那个值的行和列,由剩下的n-1阶子式就是余子式
代数余子式:在余子式前面乘个(-1)的(行+列)次幂
行列式展开公式:

重点

(5)几个重要的行列式(12 + 1)



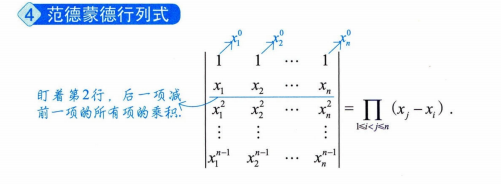
2.计算
(1)具体性

3.余子式和代数余子式的线性组合运算

注:M和A混合的也可以,直接把M变成A
4.克拉默法则

二.矩阵
1.矩阵的定义和运算

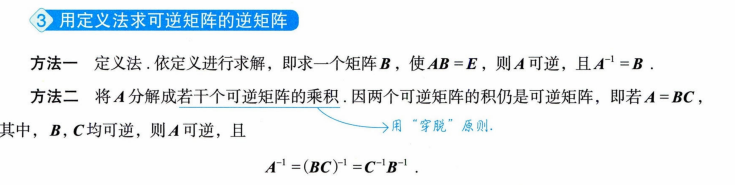
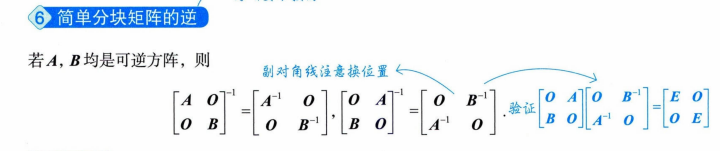
2.矩阵的逆

3.伴随矩阵

4.初等变换与初等矩阵

5.矩阵方程

6.等价矩阵与矩阵的秩

三.向量组
1.向量与向量组的线性相关性
(1)向量的定义

(2)向量的内积与正交

(3)正交矩阵

(4)线性组合

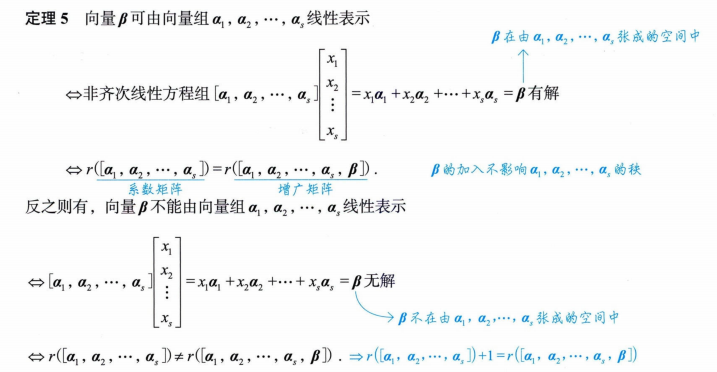
(5)线性表示

(6)线性相关性

(7)判别的7大定理


2.极大线性无关组与向量组的秩
(1)极大线性无关组
(2)向量组的秩


3.等价向量组
(1)定义

(2)与等价矩阵的区别

4.向量空间
(1)概念

(2)基变换与坐标变换公式

四.线性方程
1.齐次线性方程组
(1)有解的条件



(2)解的性质

(3)基础解系和解的结构

(4)求解方法与步骤

2.非齐次线性方程组
(1)有解的条件

(2)解的性质

(3)求解方法与步骤

3.两个方程组的公共解

4.同解方程组

五.特征方程和特征向量
1.特征值和特征向量
(1)定义

(2)求法

(3)性质和重要结论

2.相似
(1)矩阵的相似





(2)矩阵的相似对角化

(3)实对称矩阵的相似对角化

六.二次型
1.二次型的定义和矩阵表示

2.化二次型为标准形与规范型


3.正定二次型