B. Astrophysicists
题目:

 思路:
思路:
贪心数学
我们很容易想到,我们肯定是每个人分配 (g - 1) / 2 个银币最好,这样就能全贪走剩下的了,同时我们也最多只能贪这么多,我们假设给前 n-1 人分配好了这么多个(假设硬币够多),那么最后一个人最好全收下所有硬币,为什么?
如果不收下,那么就会分给别人,那么现在所贪的数量肯定不会优于之前的,最多只能等于,而最后一个人也只能贪 (g-1)/2 个硬币,所以不如全给最后一个看看还能不能贪
特别的,由于硬币数量可能不足,所以我们还需要取min
代码:
cpp
#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"
void solve()
{
int n, k, g;
cin >> n >> k >> g;
int onetake = (g - 1) / 2;
int cantake = min(onetake * n,k*g);
if (cantake == k*g)
{
cout << cantake << endl;
return;
}
cantake -= onetake;
int x = k * g - cantake;
int r = x % g;
if (r >= (g+1)/2)
{
cantake += -g + r;
}
else
{
cantake += r;
}
cout << cantake << endl;
}
signed main()
{
cin.tie(0)->sync_with_stdio(false);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}C. Vampiric Powers, anyone?
题目: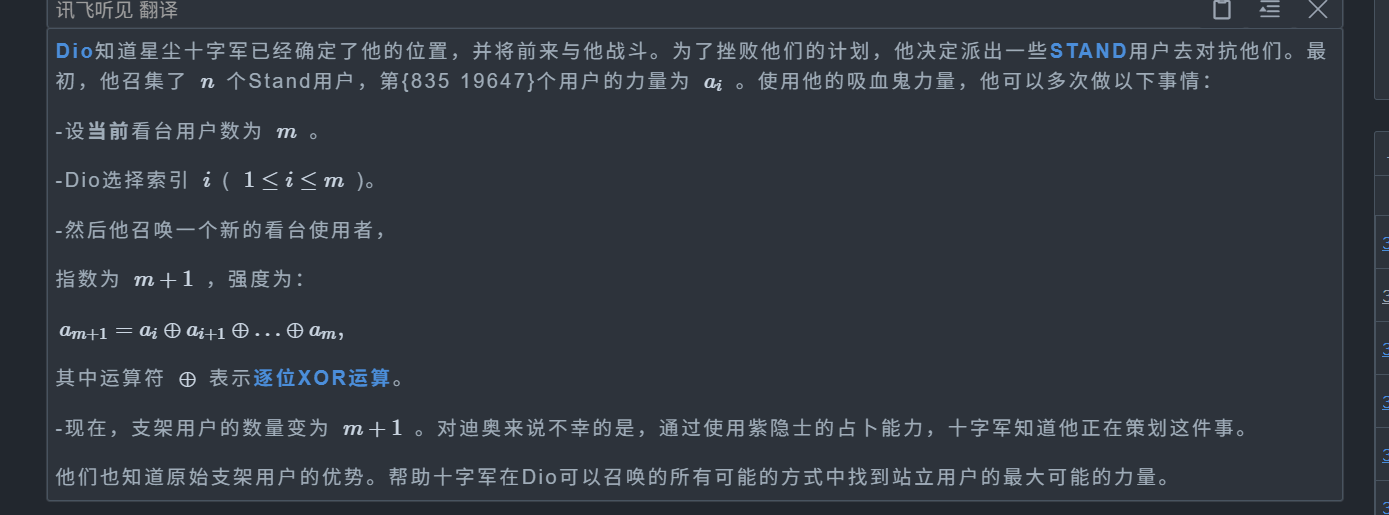
 思路:
思路:
思路题,找特性
我们来观察一下题目,题目可以让我们从后往前取一段异或和然后放到最后做一个新的值,那我们来观察一下有什么特征吗?

我们假设取了一段B放在最后,那么如果我下一步取了 A+B+B 这一段,那么最后的值就变成了 A,因为 A ^ B ^ B = A ^ 0 = A,也就是说其实我们的这个步骤是可以转化为取任意一段区间的异或和的
那么现在就变成了区间最大异或和
由于这题的数据量很小,所以我们可以考虑暴力做法
我们可以定义一个后缀异或和sum,那么对于任意一段 [l,r] 区间就可以表示为 sum[r] ^ sum[l - 1]
然后暴力枚举即可,这里可以看看cf官方的代码,还是很好懂的
当然,我们也可以使用 01Trie ,我们观察一下上面式子,其实这不就是选取最大异或对吗?所以直接套 01Trie 也可解决
代码:
cpp
#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"
void solve()
{
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; i++)
{
cin >> a[i];
}
int max_val = 1LL << 8;
vector<bool> f(max_val, 0);
f[0] = 1;
int mx = 0;
int sum = 0;
for (auto& x : a)
{
sum ^= x;
for (int i = 0; i < max_val; i++)
{
if (f[i])
mx = max(mx, sum ^ i);
}
f[sum] = 1;
}
cout << mx << endl;
}
signed main()
{
cin.tie(0)->sync_with_stdio(false);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}
cpp
#include <iostream>
#include <algorithm>
#include<cstring>
#include <iomanip>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <utility>
#include <array>
#include <tuple>
using namespace std;
#define int long long
#define yes cout << "YES" << endl
#define no cout << "NO" << endl
void solve()
{
int n;
cin >> n;
vector<vector<int>> ch((n+1) * 9, vector<int>(2, 0));
int idx = 0;
vector<int> a(n + 1);
vector<int> sum(n + 1, 0);
int ans = 0;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
sum[i] = sum[i - 1] ^ a[i];
}
auto insert = [&](int x) ->void{
int p = 0;
for (int i = 8; i >= 0; i--)
{
int j = x >> i & 1;
if (!ch[p][j])
{
ch[p][j] = ++idx;
}
p = ch[p][j];
}};
auto query = [&](int x) ->int{
int p = 0, res = 0;
for (int i = 8; i >= 0; i--)
{
int j = x >> i & 1;
if (ch[p][!j])
{
res += 1LL << i;
p = ch[p][!j];
}
else
{
p = ch[p][j];
}
}
return res;
};
insert(0);
for (int i = 1; i <= n; i++)
{
ans = max(ans, query(sum[i]));
insert(sum[i]);
}
cout << ans << endl;
}
signed main()
{
cin.tie(0)->sync_with_stdio(false);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}