目录
[5.1 频谱共享](#5.1 频谱共享)
[5.2 博弈论](#5.2 博弈论)
[5.3 基于Stackelberg博弈的频谱共享调度算法](#5.3 基于Stackelberg博弈的频谱共享调度算法)
1.引言
在5G及未来的无线通信网络中,频谱资源的高效利用是一个核心挑战。博弈论作为一种强大的数学工具,被广泛应用于频谱共享问题的研究中。其中,Stackelberg博弈和Bertrand博弈是两种常用的博弈模型,它们在频谱共享调度算法中有着不同的应用场景和性能表现。
2.算法仿真效果演示
软件运行版本:
matlab2024b
仿真结果如下**(仿真操作步骤可参考程序配套的操作视频,完整代码运行后无水印)**:



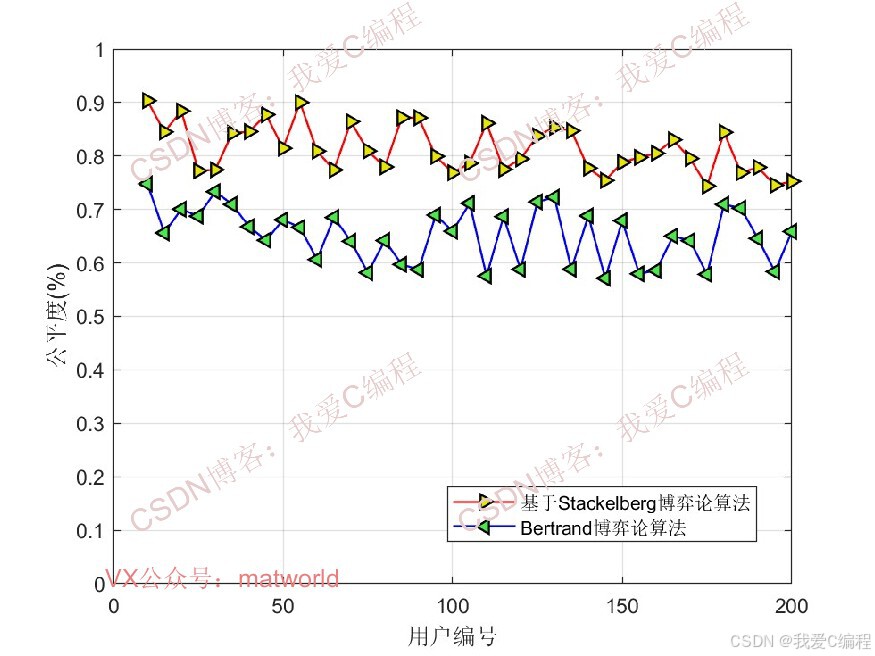

3.数据集格式或算法参数简介
SCALE = 100;
NUM = 200;
%分布
XYcas = SCALE/40*rand(2,NUM);
XYdas1= SCALE/12+SCALE/10*rand(2,NUM);
xl = [0:0.5:10];%频谱效率
Width = [0:1:15]; %可出租的频偏资源数量4.MATLAB部分程序
核心代码见完整工程
figure;
plot(Width,mean(P2,2),'-r>',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.9,0.0]);
hold on
plot(Width,mean(P1,2),'-b<',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.3,0.9,0.3]);
hold on
grid on
xlabel('可共享的资源频谱(MHz)');
legend('基于Stackelberg博弈论算法','Bertrand博弈论算法');
ylim([5,40]);
ylabel('定价');
01_233m5.算法涉及理论知识概要
频谱共享是指多个无线通信系统或用户共享同一频段的频谱资源,以提高频谱利用率。传统的固定频谱分配方式导致频谱利用率低下,而动态频谱共享技术可以显著提高频谱资源的使用效率。
5.1 频谱共享
在频谱共享场景中,通常存在以下参与者:
主用户 (PU, Primary User):拥有频谱授权的用户
次用户 (SU, Secondary User):不拥有频谱授权,但可以在不干扰主用户的前提下使用频谱的用户
频谱共享的目标是在满足主用户 QoS 要求的前提下,最大化次用户的频谱利用率或系统总效益。
5.2 博弈论
博弈论是研究决策主体在相互作用时的决策以及这种决策的均衡问题的理论。一个标准的博弈模型包括以下要素:
参与者 (Players):参与博弈的决策主体
策略集 (Strategies):每个参与者可以选择的策略集合
收益函数 (Payoff Functions):描述每个参与者在不同策略组合下的收益
博弈论可以分为合作博弈和非合作博弈。在非合作博弈中,参与者之间无法达成具有约束力的协议,每个参与者都追求自身利益的最大化。Stackelberg 博弈和 Bertrand 博弈都属于非合作博弈。
5.3 基于Stackelberg博弈的频谱共享调度算法
Stackelberg博弈是一种序贯博弈,由德国经济学家Heinrich von Stackelberg在1934年提出。在Stackelberg博弈中,参与者分为领导者 (Leader) 和追随者 (Follower):
领导者:首先行动,制定自己的策略
追随者:在观察到领导者的策略后,制定自己的策略
Stackelberg博弈的求解过程是逆向归纳法:首先求解追随者的最优反应函数,然后将该反应函数代入领导者的收益函数,求解领导者的最优策略。
一个标准的 Stackelberg 博弈模型可以表示为:
参与者:领导者 (L) 和追随者 (F)
策略集:领导者的策略空间为SL,追随者的策略空间为SF
收益函数:领导者的收益函数为uL(sL,sF),追随者的收益函数为uF(sL,sF),其中sL∈SL,sF∈SF
求解步骤:

在频谱共享场景中,Stackelberg 博弈通常适用于以下情况:
主用户 - 次用户关系:主用户作为领导者,次用户作为追随者;
运营商 - 用户关系:运营商作为领导者,用户作为追随者;
异构网络场景:宏基站作为领导者,小基站作为追随者;
在这些场景中,领导者通常拥有更多的资源或决策权,可以先行动并影响追随者的决策。
考虑一个频谱共享系统,由一个主用户 (PU) 和多个次用户 (SU) 组成。主用户拥有频谱资源,并可以将部分频谱出租给次用户使用。次用户可以选择租赁不同数量的频谱资源,以最大化自己的收益。主用户的收益来自于出租频谱的收入减去由于次用户使用频谱带来的干扰成本:

6.参考文献
1\]秦文丽.基于博弈论的认知无线电频谱共享算法研究\[D\].北京交通大学\[2025-06-19\].DOI:10.7666/d.y1340703. \[2\]廖天.基于Stackelberg博弈论的分布式天线系统频谱共享调度机理研究\[D\].深圳大学,2020. ## 7.完整算法代码文件获得 **完整程序见博客首页左侧或者打开本文底部** **V**