在之前的《slam中的eskf推导》一文中,没有写观测矩阵 H 矩阵的过程,现在补上这部分。
前置
列举几个等下推导需要用到的一些点:

平面特征点构造观测矩阵
例如在 fastlio 中,是利用平面特征点到拟合平面的距离来构造观测方程,利用平面特征点到拟合平面的距离应该趋向于0来列方程。假设拟合后的法向量为 u = [A, B, C]',截距为 D,点到平面的距离为 d = Ax + By + Cz + D。
以距离来列观测方程:
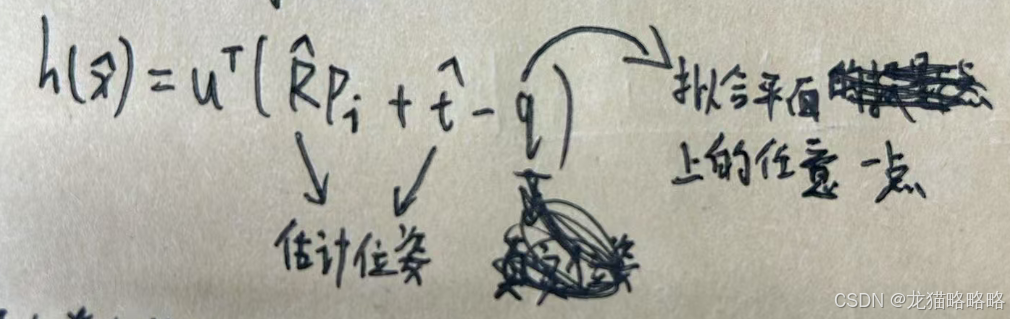
对于 q 点的解释
对于平面方程,可以写作:
u'(x - q) = 0
u 是单位法向量,q 是平面上的任意已知点,点到平面的距离可以写作:
d = u'(x - q)
如果 x 也在平面上,则 d = 0
q 的选取不影响距离值的计算,因为:
u'(x - q1) = u'(x - q2)
推导观测方程
添加姿态偏差 δR,平移偏差 δt,以及噪声 V:

变换式子,可以得到:
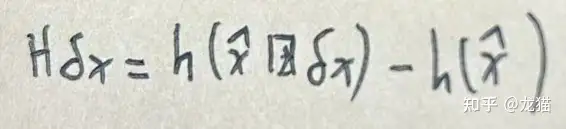
等式两边对 δx 求偏导,得:

之后对 δx 中的角度 δθ 和 位移 δt 分别求偏导,得到:

对 δt 求偏导就比较简单了:
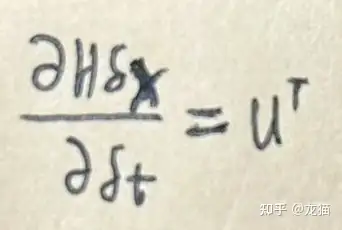
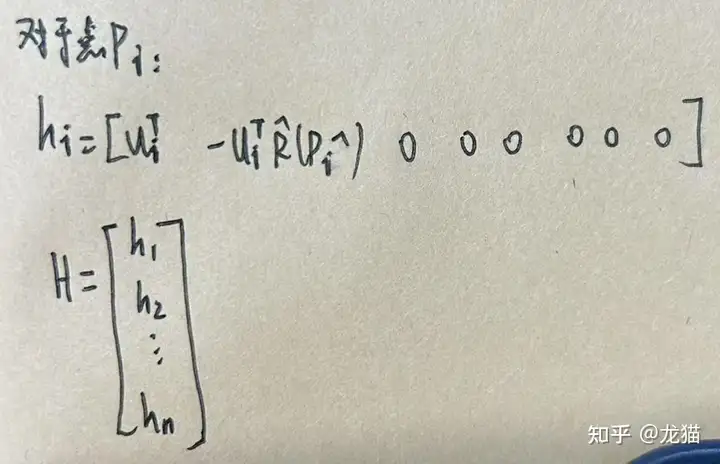
那么对于点 Pi 以及整体的观测矩阵 H: