1. 线性回归模型
1.1 线性回归模型
线性回归模型:将数据拟合成一条直线。
作用:预测数字作为输出。
例子:
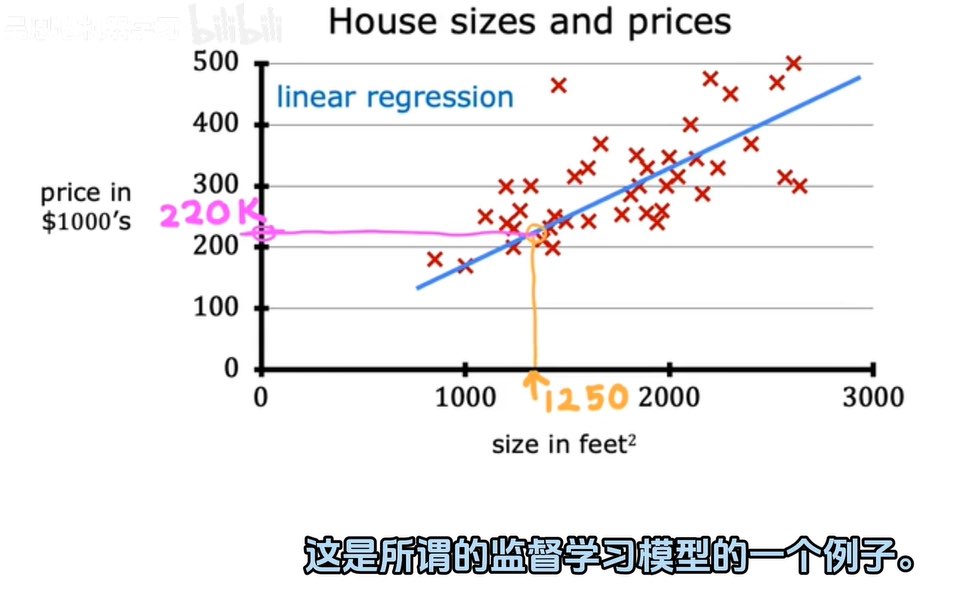
房子的大小与房价的估计
(图表)
(数据表)
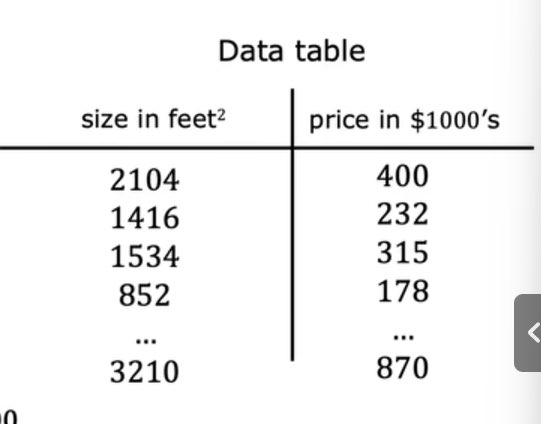
1.2 训练集
训练集:用于训练模型的数据集
训练集作业例子:要预测客户的房价,首先要训练模型以从训练集中学习,然后该模型可以预测客户的房价。
输入的标准符号:x(输入变量/特征/输入特征)
预测的输出变量的标准符号:y(目标变量)
单个训练示例:(x,y)
引用一个具体的训练例子:
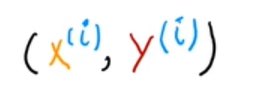
i表示第几个训练示例。
1.3 监督学习的工作工作过程
要训练模型,需要将训练集(包括输入特征和输出目标)提供给学习算法。然后监督学习算法会产生一些功能(函数f)。
函数f:输入x,输出预测y值。
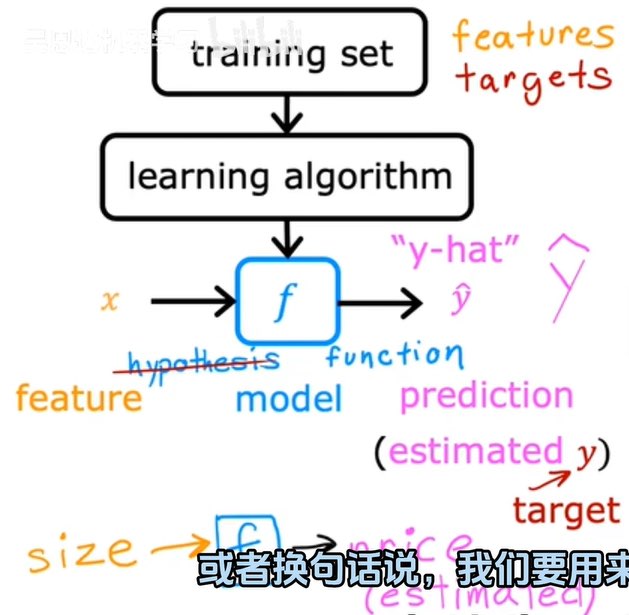
如何表示函数f:
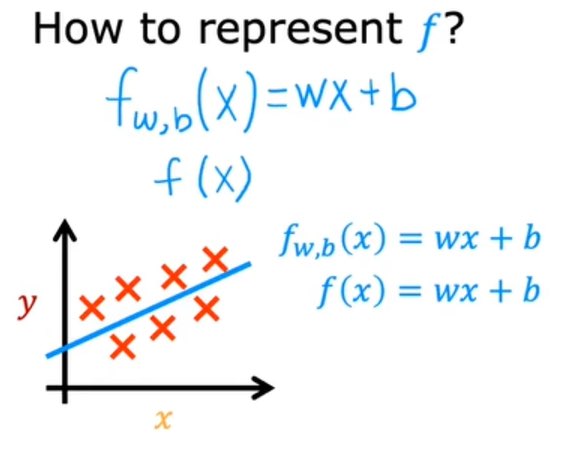
上面的直线即单线性回归模型。
1.4 代价函数/成本函数
代价函数:表示一个用于衡量模型预测值与真实值之间差异的函数,目标是通过最小化这个函数来优化模型参数。
成本函数(平方误差成本函数):
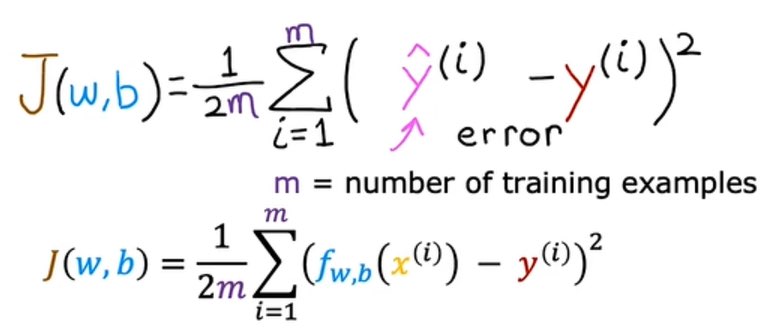
成本函数在三个维度:
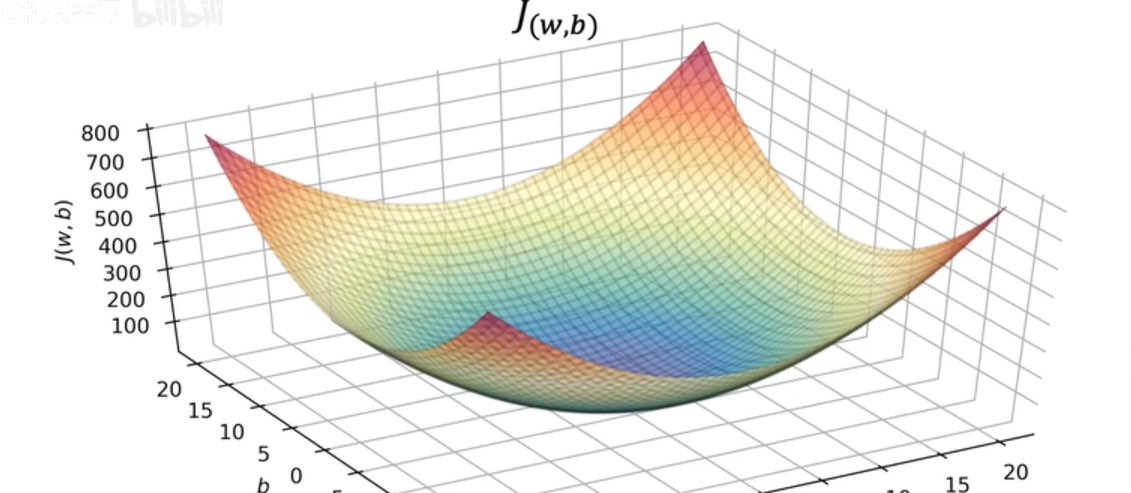
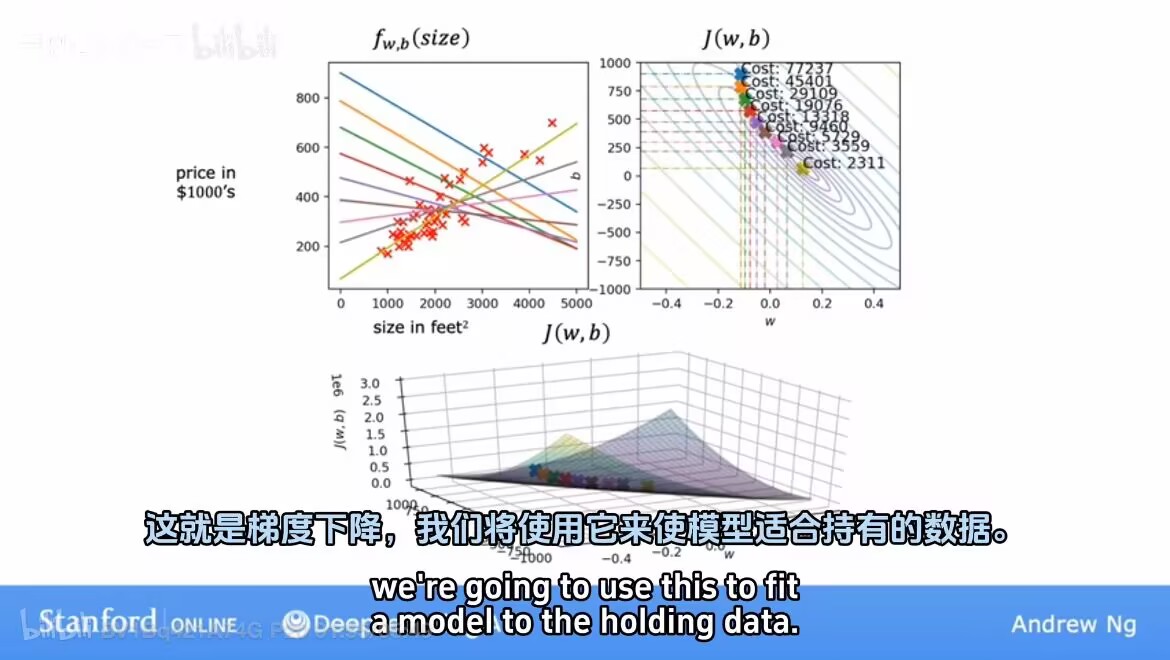
如何实现最小化成本函数---梯度算法。
2. 梯度算法
2.1 梯度算法
梯度算法:每次稍微改变参数w和b以尝试降低w和b的成本j,知道希望j稳定最小值或者接近最小值。对于某些可能不是弓形或者吊床形的函数j,可能存在不止一个最小值。

2.2 实现梯度下降
梯度下降算法:

a:学习率,取值0~1,控制下坡步幅。
导数:成本函数j的导数项,控制往哪个方向迈步。
2.3 梯度下降的直观理解

上面解释了w会正确移向最低点。
2.4 学习率
a太小时:梯度下降会起作用,但是下降的速度太慢。
a太大时:梯度下降可能会超过,并且可能永远不会达到。(梯度下降可能无法达到收敛,甚至可能发散)
当更新时候w不变,表示参数已经使得j达到局部最小值。
当接近局部最小梯度下降时,会自动采取更小的步长。(因为斜率在变小)
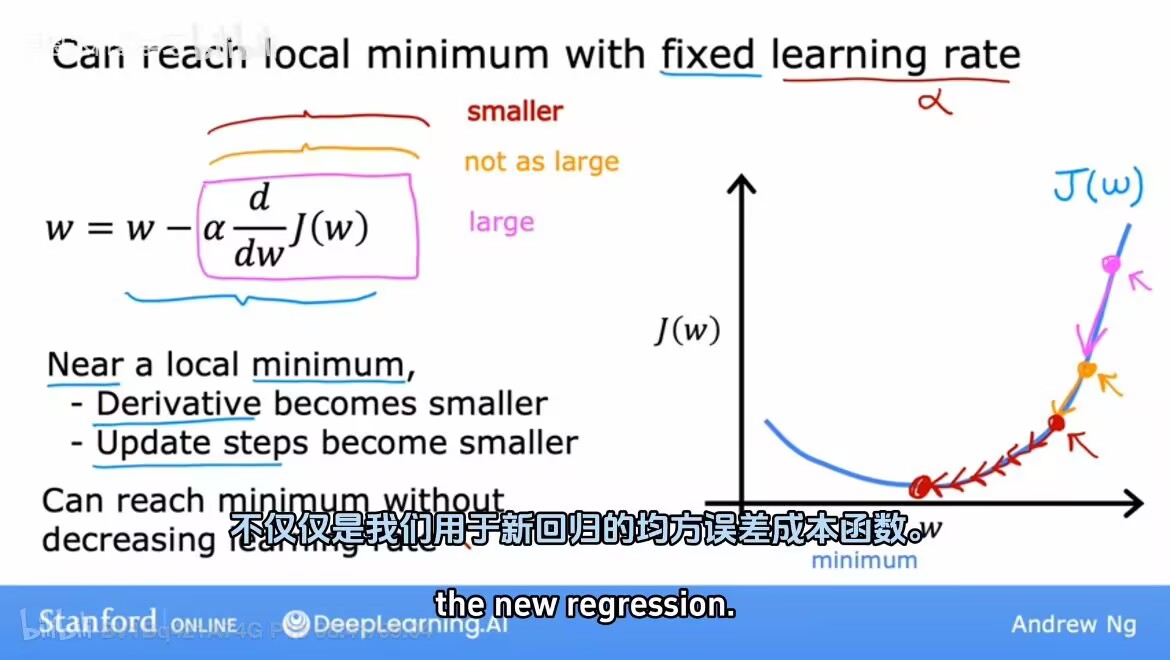
2.5 线性回归中的梯度下降

重复执行上面式子知道收敛为止。
运行梯度下降: