链表算法---基本算法操作（go语言版）

一.链表基本结构定义

链表的基础结构是节点，Go 语言实现如下：

go 复制代码

type ListNode struct {  
    Val  int  
    Next *ListNode  
}

二.基础操作

创建链表（数组转链表）

go 复制代码

func BuildList(nums []int) *ListNode {  
    dummy := &ListNode{}  
    cur := dummy  
    for _, v := range nums {  
        cur.Next = &ListNode{Val: v}  
        cur = cur.Next  
    }  
    return dummy.Next  
}

遍历链表

go 复制代码

func Traverse(head *ListNode) {  
    for head != nil {  
        fmt.Println(head.Val)  
        head = head.Next  
    }  
}

插入节点

头插法（O(1)）：

go 复制代码

func InsertHead(head *ListNode, val int) *ListNode {  
    return &ListNode{Val: val, Next: head}  
}

尾插法（O(n)）：

go 复制代码

func InsertTail(head *ListNode, val int) *ListNode {  
    if head == nil {  
        return &ListNode{Val: val}  
    }  
    cur := head  
    for cur.Next != nil {  
        cur = cur.Next  
    }  
    cur.Next = &ListNode{Val: val}  
    return head  
}

删除节点

go 复制代码

func DeleteNode(head *ListNode, val int) *ListNode {  
    dummy := &ListNode{Next: head}  
    cur := dummy  
    for cur.Next != nil {  
        if cur.Next.Val == val {  
            cur.Next = cur.Next.Next  
            break  
        }  
        cur = cur.Next  
    }  
    return dummy.Next  
}

三.常见算法题

1.反转链表

核心思想：指针反转 + 三指针遍历

链表无法随机访问，只能移动指针，因此反转时需要：

cur：当前节点
prev：新链表的头
next：提前保存 cur 的下一节点，防止链断掉

go 复制代码

func ReverseList(head *ListNode) *ListNode {  
    var prev *ListNode  
    cur := head  
    for cur != nil {  
        next := cur.Next  
        cur.Next = prev  
        prev = cur  
        cur = next  
    }  
    return prev  
}

2.快慢指针查找中间节点

核心思想：快慢指针

slow 每次走 1 步
fast 每次走 2 步
当 fast 到尾部时，slow 刚好在中点

无需统计长度，O(n) 一次遍历完成。

go 复制代码

func MiddleNode(head *ListNode) *ListNode {  
    slow, fast := head, head  
    for fast != nil && fast.Next != nil {  
        slow = slow.Next  
        fast = fast.Next.Next  
    }  
    return slow  
}

3.判断链表是否有环

核心思想：Floyd 环检测算法

依旧使用快慢指针：

若存在环，fast 迟早会追上 slow
若不存在环，fast 会先遇到 nil

这是数学证明过的最优做法。

go 复制代码

func HasCycle(head *ListNode) bool {  
    slow, fast := head, head  
    for fast != nil && fast.Next != nil {  
        slow = slow.Next  
        fast = fast.Next.Next  
        if slow == fast {  
            return true  
        }  
    }  
    return false  
}

4.合并两个有序链表

核心思想：双指针 + 有序合并（类似归并排序 Merge 阶段）

两个链表都已经排序，因此：

每次取两链表头部较小的节点
挂到新链表后面
移动取自的链表的指针

最终形成一个整体有序的链表。

go 复制代码

func MergeTwoLists(l1, l2 *ListNode) *ListNode {  
    dummy := &ListNode{}  
    cur := dummy  
    for l1 != nil && l2 != nil {  
        if l1.Val < l2.Val {  
            cur.Next = l1  
            l1 = l1.Next  
        } else {  
            cur.Next = l2  
            l2 = l2.Next  
        }  
        cur = cur.Next  
    }  
    if l1 != nil {  
        cur.Next = l1  
    }  
    if l2 != nil {  
        cur.Next = l2  
    }  
    return dummy.Next  
}

5.删除倒数第 N 个节点

核心思想：快慢指针 + 间隔法

为了一次遍历就定位倒数第 N：

先让 fast 先走 N 步
然后 slow 和 fast 一起走
当 fast 到尾时，slow 刚好指向倒数第 N 的前一个节点

删除 slow 后的节点即可。

go 复制代码

func RemoveNthFromEnd(head *ListNode, n int) *ListNode {  
    dummy := &ListNode{Next: head}  
    fast, slow := dummy, dummy  
    for i := 0; i < n; i++ {  
        fast = fast.Next  
    }  
    for fast.Next != nil {  
        fast = fast.Next  
        slow = slow.Next  
    }  
    slow.Next = slow.Next.Next  
    return dummy.Next  
}

6.链表排序（归并排序）

核心思想：归并排序（Merge Sort on Linked List）

链表不适合快排（无法随机访问，pivot 划分难且不稳定）
最适合的是：归并排序

过程：

快慢指针找中点 → 分成左右两半
递归排序左右链表
合并两条有序链表（复用 MergeTwoLists）

时间：O(n log n)

空间：O(log n)（递归栈）

go 复制代码

func SortList(head *ListNode) *ListNode {  
    if head == nil || head.Next == nil {  
        return head  
    }  
    slow, fast := head, head.Next  
    for fast != nil && fast.Next != nil {  
        slow = slow.Next  
        fast = fast.Next.Next  
    }  
    mid := slow.Next  
    slow.Next = nil  
    left := SortList(head)  
    right := SortList(mid)  
    return MergeTwoLists(left, right)  
}

7.判圈算法

在力扣环形链表Ⅱ中，判断是否有环形链表，及找到入环点

1.判断是否有环形链表

方法一：用map的key唯一来判断当到同一个结点时就是环形链表同时返回入环点

方法二：用快，慢结点。快结点走两个结点，慢结点走一个，如果是环形链表肯定会相遇，如果不是在快结点走到尾返回

2.用方法二，利用判圈算法找到入环点

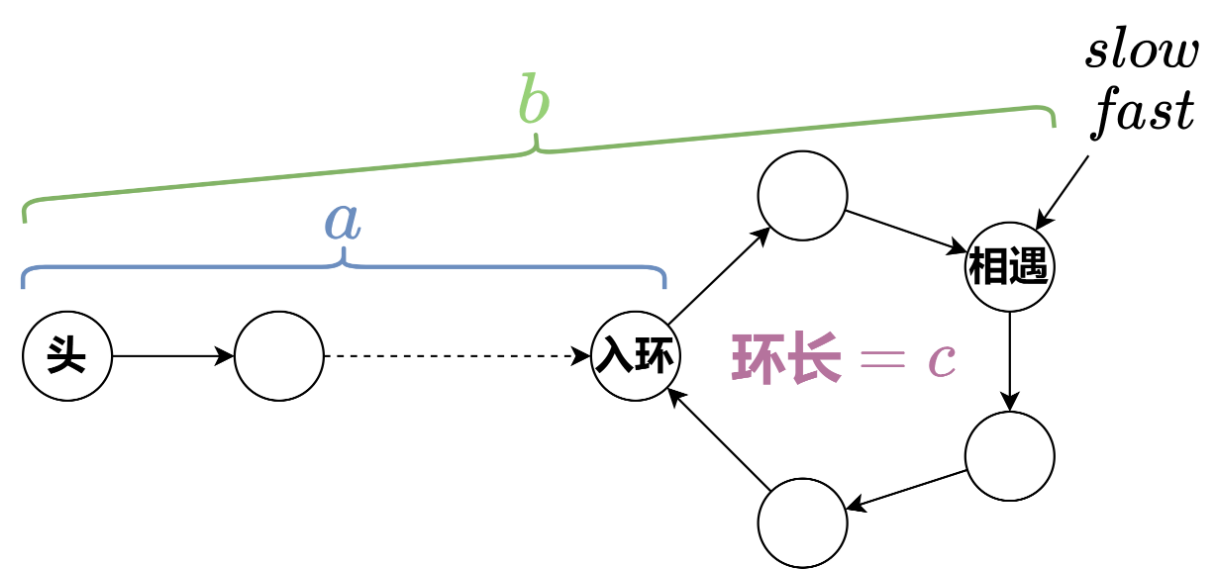
首先：假设慢结点走了b步，则快结点走了2b步，设环长为c，快结点比慢结点在相遇时在环中走了多走了k圈，则2b-b=kc。

其次：设从头结点到入环点的长度为a，则b-a就是慢结点在环中走的路程=kc-a。

最后：慢结点在走a步就能到达入环点（初始位置），并且头结点到达入环点的位置也是a。

8.链表相交

算法思路：双指针 A + B（不等长链表齐头并进法）
将两个链表 A 和 B 视为不同长度的路径：

A: a₁ → a₂ → a₃ → c₁ → c₂
B: b₁ → b₂ → c₁ → c₂

关键点：

使用两个指针 pA 和 pB，分别从链表 A 和 B 的头节点开始遍历。
当指针走到链表末尾时，切换到另一条链表的头部继续遍历：
- pA 的路径：A → B
- pB 的路径：B → A

数学逻辑 ：

由于 len(A) + len(B) = len(B) + len(A)，若存在相交节点，两指针会在同一节点相遇（即交点）。若不相交，两指针最终会同时到达 null。

效率分析：

时间复杂度：O(m + n)，其中 m 和 n 分别为链表 A 和 B 的长度。
空间复杂度：O(1)，仅使用常数级额外空间。

Go 复制代码

func GetIntersectionNode(headA, headB *ListNode) *ListNode {
    if headA == nil || headB == nil {
        return nil
    }

    pA := headA
    pB := headB

    for pA != pB {
        if pA == nil {
            pA = headB   // A 走完，切换到 B
        } else {
            pA = pA.Next
        }

        if pB == nil {
            pB = headA   // B 走完，切换到 A
        } else {
            pB = pB.Next
        }
    }

    return pA  // 交点 or nil
}

四.进阶专题

K 个一组翻转链表
链表加法（两数相加）
复制带随机指针的链表
LRU 缓存（双向链表 + Hash）
扁平化多级双向链表