本期我们将深入学习C++中关于STL容器的容器类型:stack(栈)和deque(队列)
作者本人的gitee:楼田莉子 (riko-lou-tian) - Gitee.com
目录
[top(取栈顶元素 )](#top(取栈顶元素 ))
[编辑 swap](#编辑 swap)
[编辑 swap](#编辑 swap)
[编辑 emplace](#编辑 emplace)
stack的介绍和官方文档
官方文档: stack - C++ 参考
stack的介绍
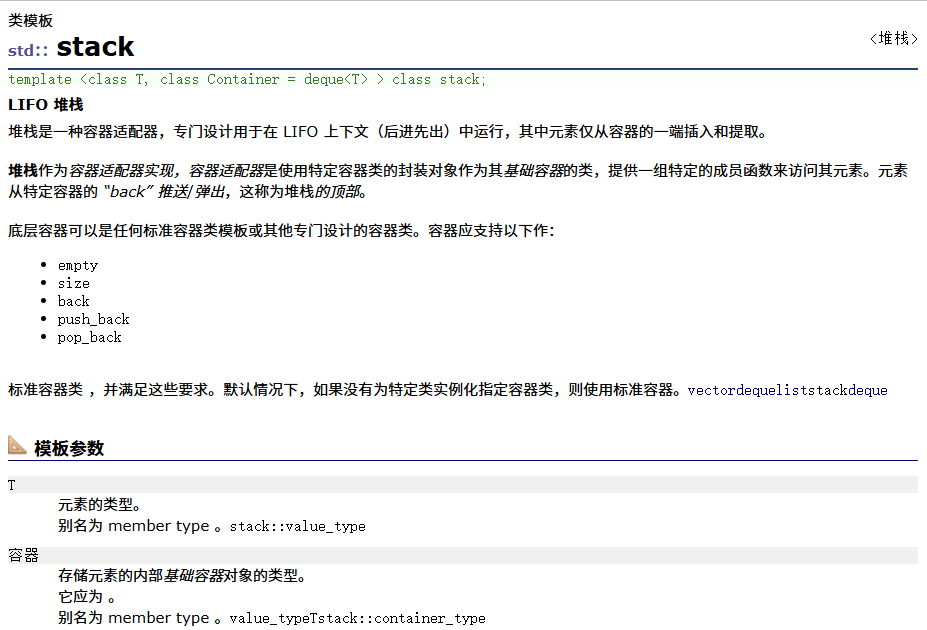
stack的构造函数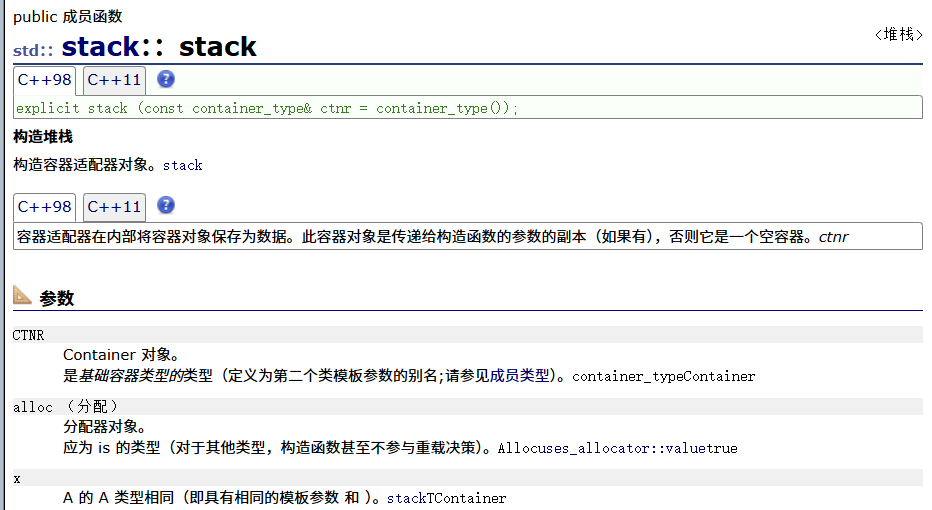
stack不支持迭代器遍历,因此stack也不支持范围for。
stack相关的函数
empty(判空)
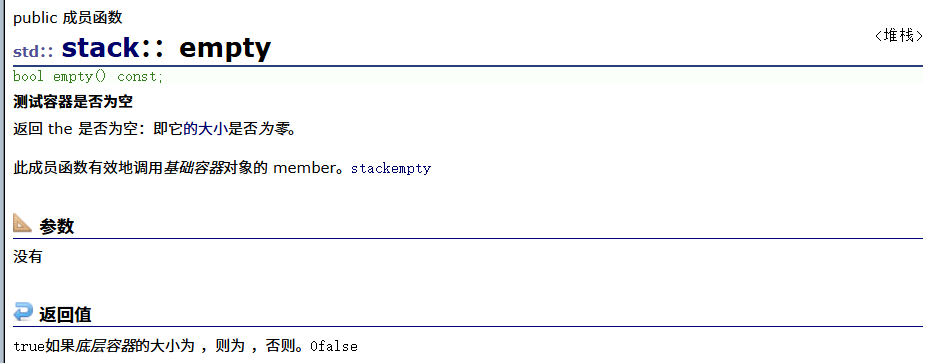
push(入栈)
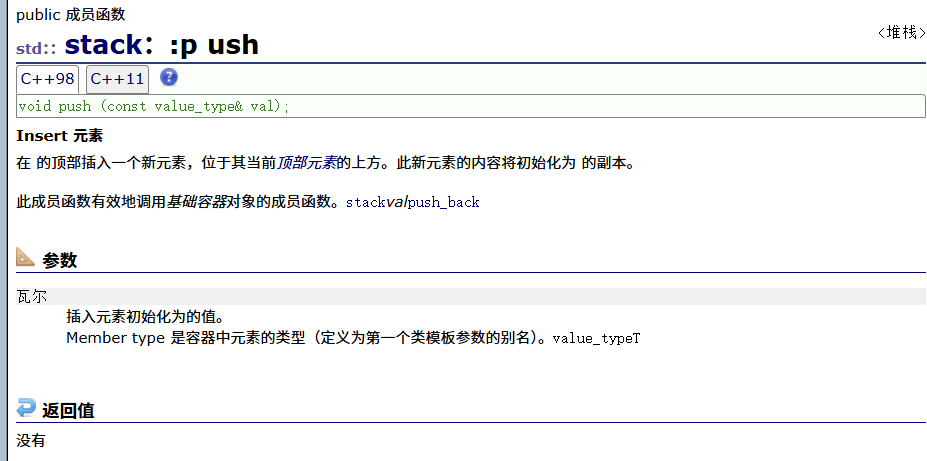
pop(出栈)
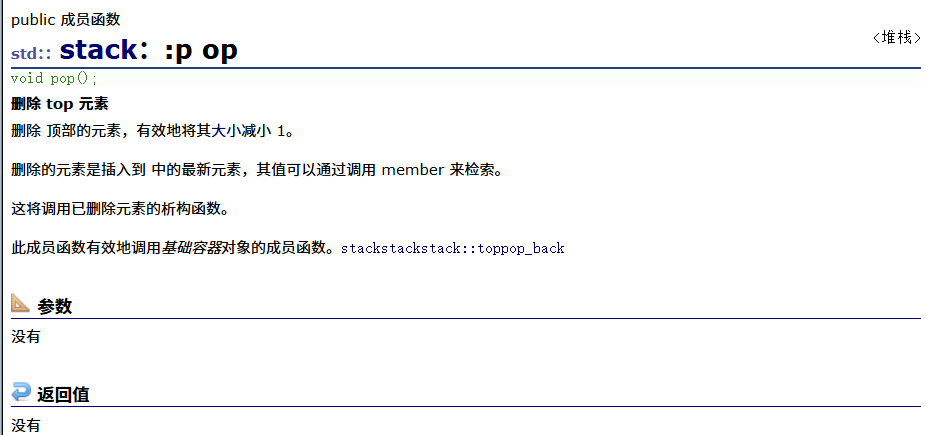
top(取栈顶元素 )
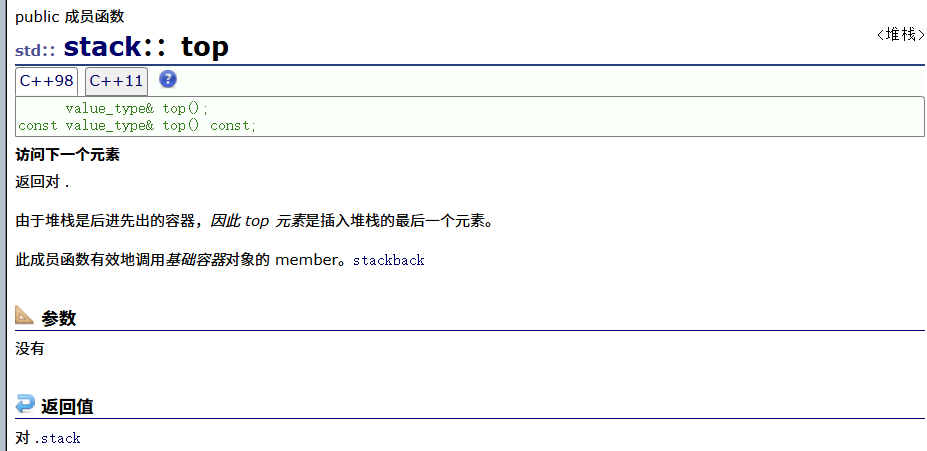
测试:
cpp
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<stack>
using namespace std;
void test1()
{
stack<int> s;
s.push(1);
s.push(2);
s.push(3);
s.push(4);
while (!s.empty())
{
cout << s.top() << " ";
s.pop();
}
cout << endl;
}
int main()
{
test1();
return 0;
}结果为:

size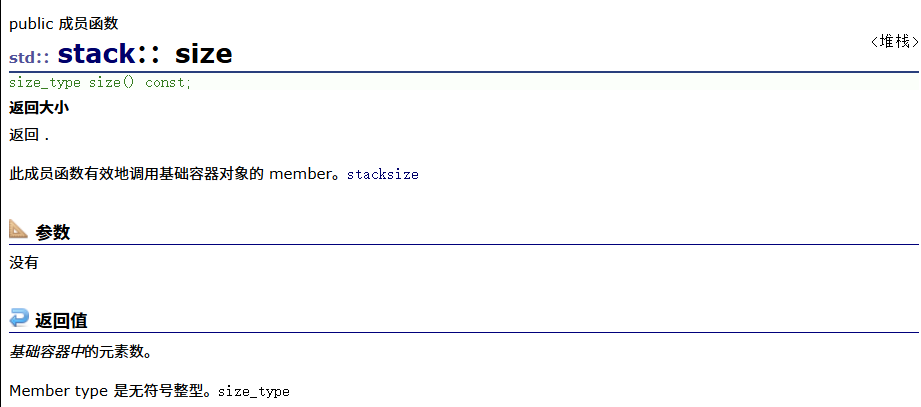
emplace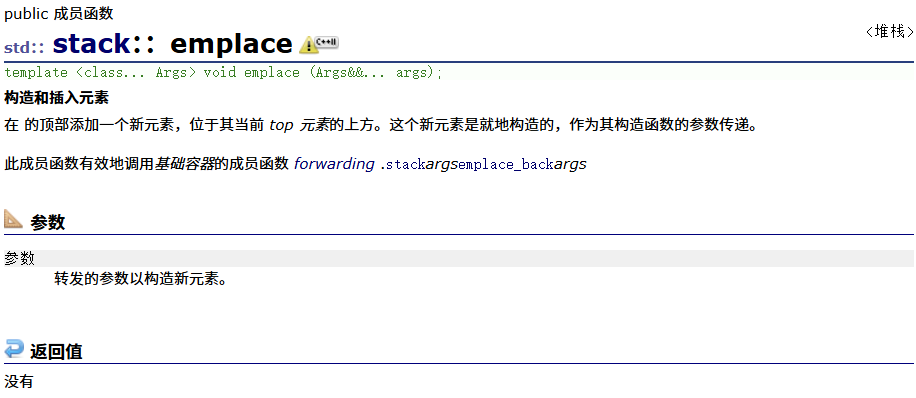
swap
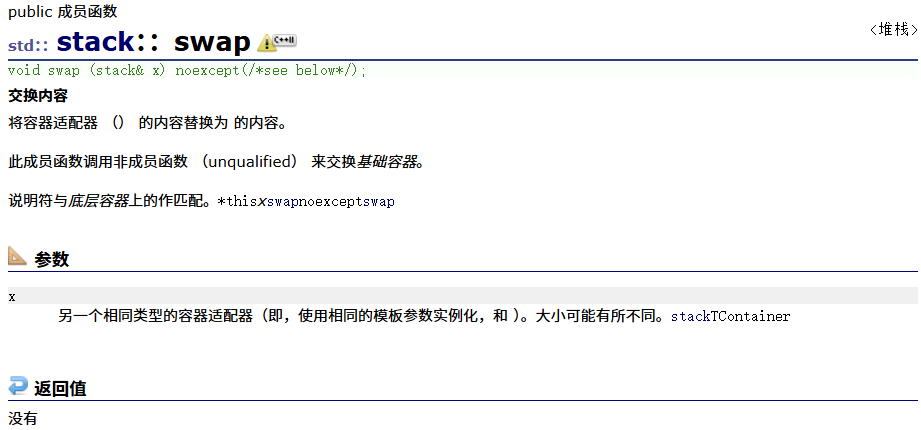
stack的模拟实现
cpp
#pragma once
#include <iostream>
#include<vector>
#include<list>
#include<deque>
using namespace std;
namespace Boogiepop
{
//适配器/配接器 //用缺省值可以不传递第二个模板参数
template<class T, class container=deque<T>>
//适配器是用来实现转换的
//本质上是容器适配器
//用容器适配转换出来的
class stack
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_back();
}
size_t size() const
{
return _con.size();
}
bool empty() const
{
return _con.empty();
}
const T& top() const
{
return _con.back();
}
private:
container _con;
};stack相关题目
1、最小栈

题目中"在常数时间内获取最小栈"意思是getmin()函数的时间复杂度是O(1).
答案:
cpp
class MinStack {
public:
MinStack()
{
}
void push(int val)
{
_st.push(val);
if(_minst.empty()||val<=_minst.top())
{
_minst.push(val);
}
}
void pop()
{
if(_st.top()==_minst.top())
{
_minst.pop();
}
_st.pop();
}
int top()
{
return _st.top();
}
int getMin()
{
return _minst.top();
}
private:
stack<int> _st;
stack<int> _minst;
};
/**
* Your MinStack object will be instantiated and called as such:
* MinStack* obj = new MinStack();
* obj->push(val);
* obj->pop();
* int param_3 = obj->top();
* int param_4 = obj->getMin();
*/2、栈的压入弹出序列
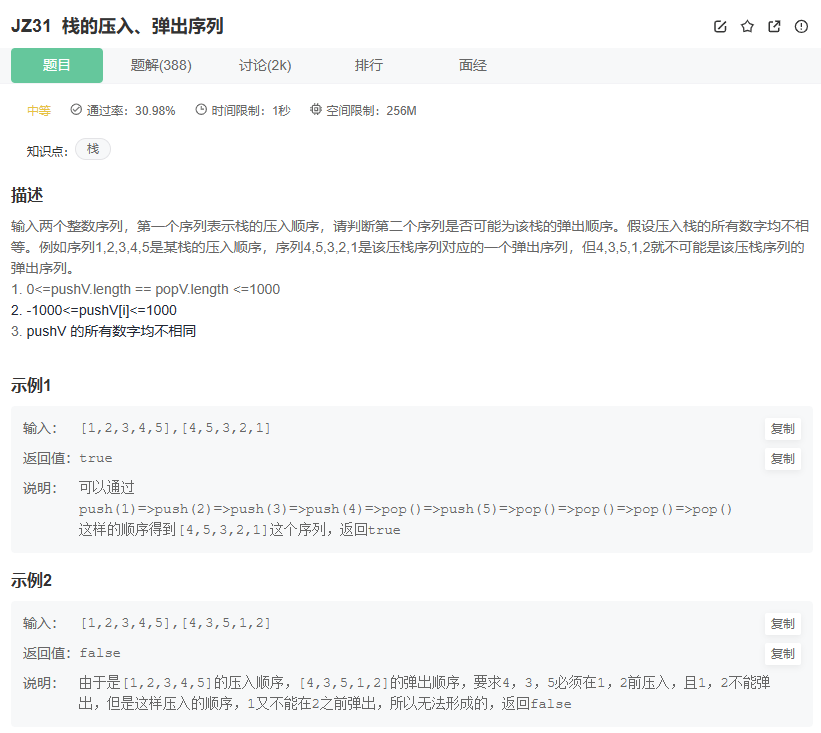
本题中从大小关系入手是没有意义的。
思路是模拟出入栈顺序跟出栈顺序匹配
思路如下:
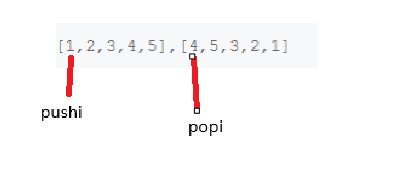
1、pushi指向的数据入栈
2、持续地让栈中数据与popi比较。如果想等则popi++,出栈顶数据,直到为空或者不匹配。
3、重复1、2 步
核心原则:持续比较
结束条件:pushi走到尾部
cpp
class Solution
{
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pushV int整型vector
* @param popV int整型vector
* @return bool布尔型
*/
bool IsPopOrder(vector<int>& pushV, vector<int>& popV)
{
// write code here
stack<int> st;
size_t pushi=0,popi=0;
while(pushi<pushV.size())
{
//先入栈
st.push(pushV[pushi++]);
//尝试与出栈序列匹配
while(!st.empty()&&st.top()==popV[popi])
{
popi++;
st.pop();
}
}
return st.empty();
}
};3、逆波兰表达式求值


逆波兰表达式的解释和扩展:【数据结构】你知道波兰表达式和逆波兰表达式吗?我才知道原来栈在表达式求值中还能这样使用......-腾讯云开发者社区-腾讯云 简单来说,计算机的运算表达式有三种:
中缀表达式(最常用的):运算数+运算符+运算数
前缀表达式:运算符+运算数+运算数
后缀表达式:运算数+运算数+运算符
所以本质上逆波兰表达式就是后缀表达式
后缀表达式运算符按优先级排列,而且要挨着要运算的运算数。
思路:
1、运算数入栈
2、如果是运算符,则出栈顶的两个数据,然后继续入栈
这里额外科普一个string的应用:将string转化为整数
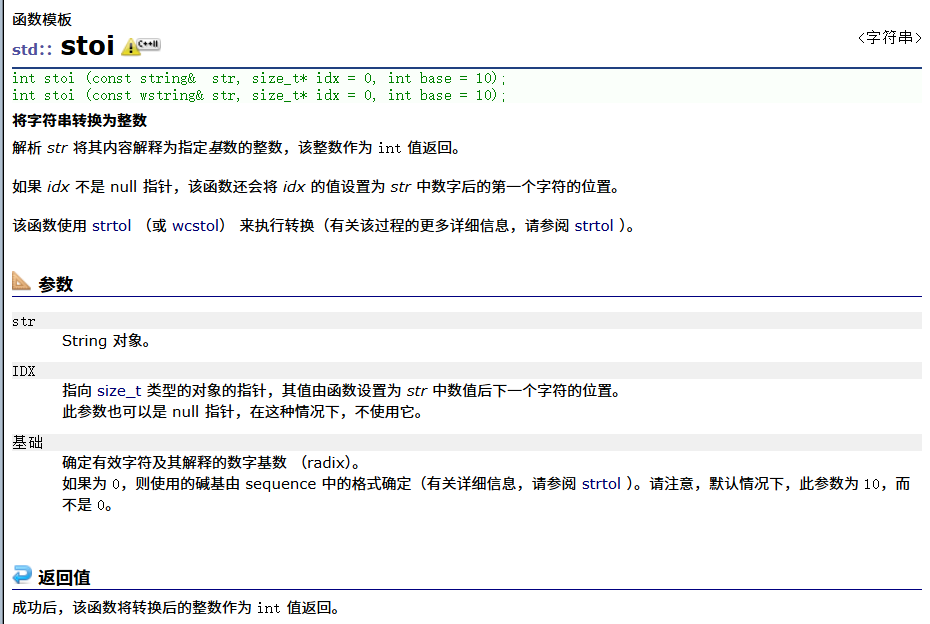
答案:
cpp
class Solution {
public:
int evalRPN(vector<string>& tokens)
{
stack<int> st;
for(auto& str:tokens)
{
if(str=="+"||str=="-"||str=="*"||str=="/")
{
//遇到运算符要出栈两个运算数然后运算后入栈
int right=st.top();
st.pop();
int left=st.top();
st.pop();
switch(str[0])
{
case '+':
st.push(left+right);
break;
case '-':
st.push(left-right);
break;
case '*':
st.push(left*right);
break;
case '/':
st.push(left/right);
break;
default:
break;
}
}
else
{
//运算数入栈
st.push(stoi(str));
}
}
return st.top();
}
};4、用栈实现队列


5、二叉树层序遍历
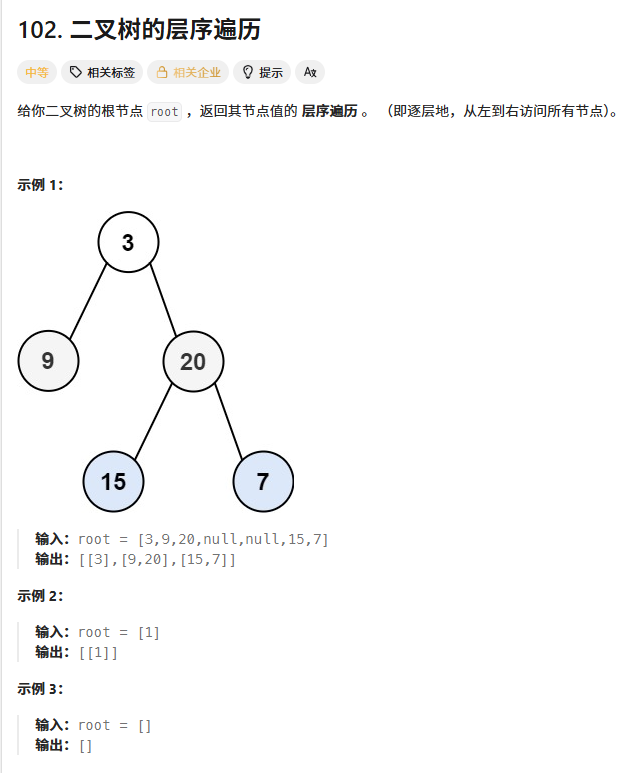
cpp
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root)
{
queue<TreeNode*>q;
int levelsize=0;//记录当前层数多少个数据
if(root)
{
q.push(root);
levelsize=1;
}
vector<vector<int>>vv;
//层序遍历
while(!q.empty())
{
vector<int>v;
//控制一层一层出
while(levelsize--)
{
TreeNode*front=q.front();
q.pop();
v.push_back(front->val);
if(front->left)
{
q.push(front->left);
}
if(front->right)
{
q.push(front->right);
}
}
vv.push_back(v);
//当前层出完了下一层节点都进队列,队列数据个数就是下一次节点个数
levelsize=q.size();
}
return vv;
}
};这段代码的时间复杂度不是O(N^2)。因为队列进入和出只用了N次。所以实际上时间复杂度是O(N)
queue的介绍和官方文档
官方文档:
queue(单端队列)的介绍
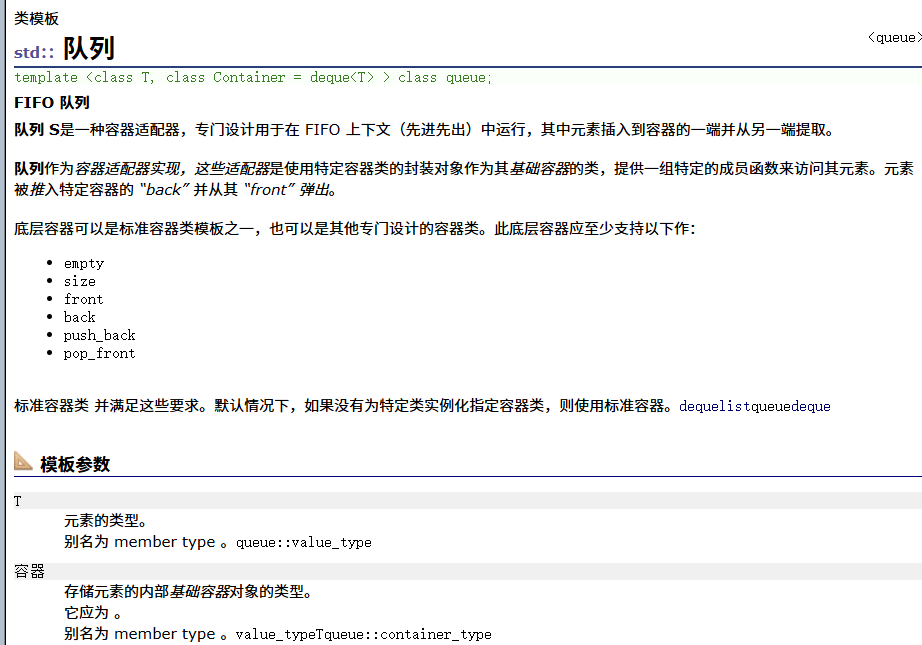
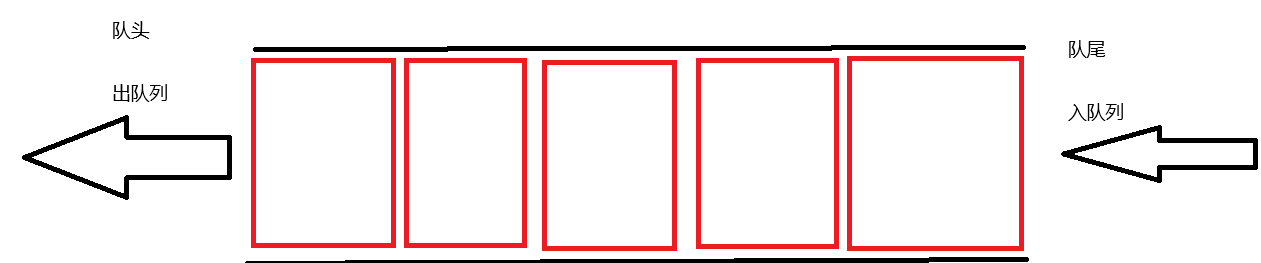
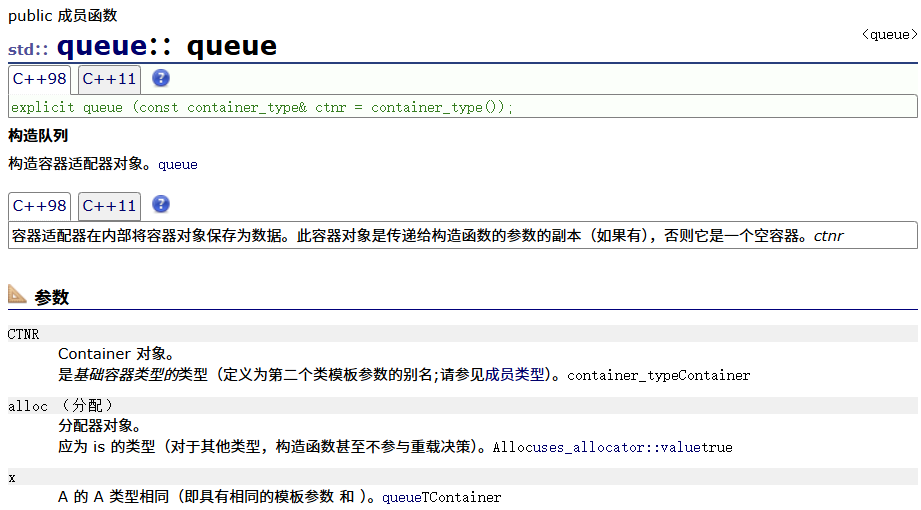
queue构造函数
queue相关的函数
empty

size
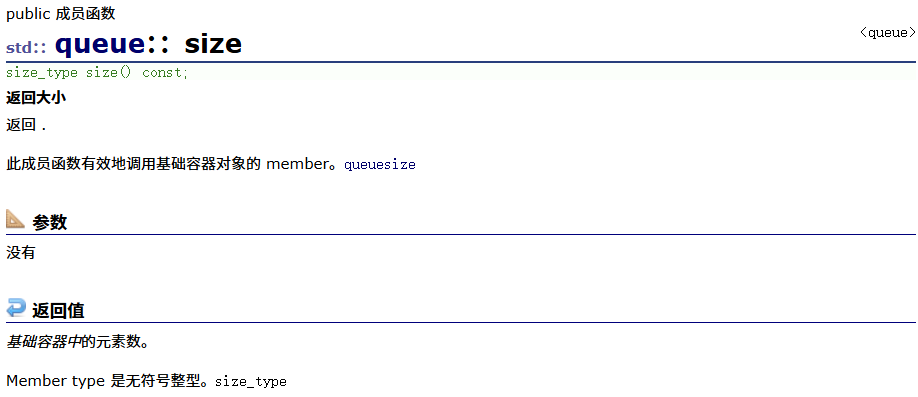
front
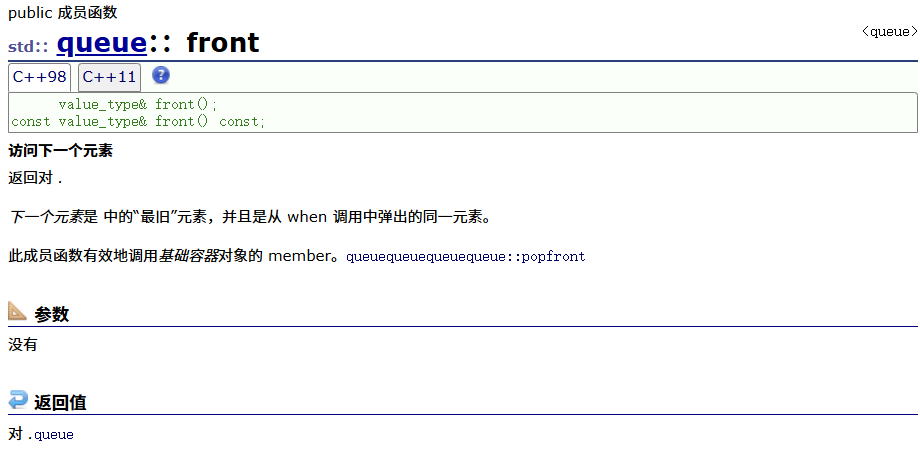
back
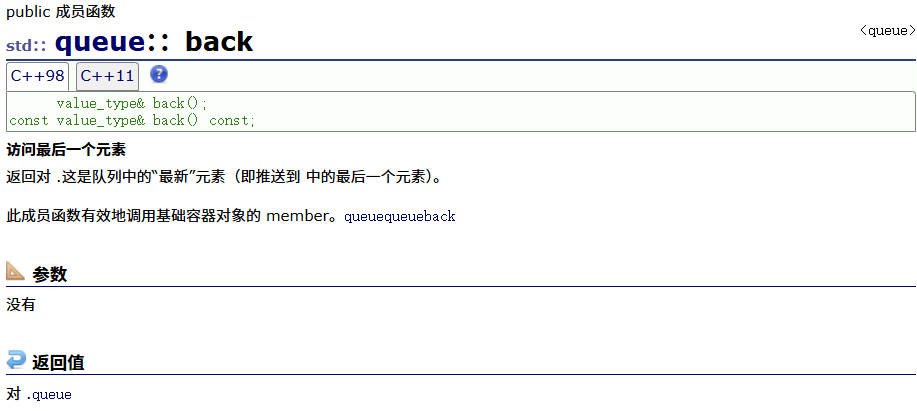
push(入队列)
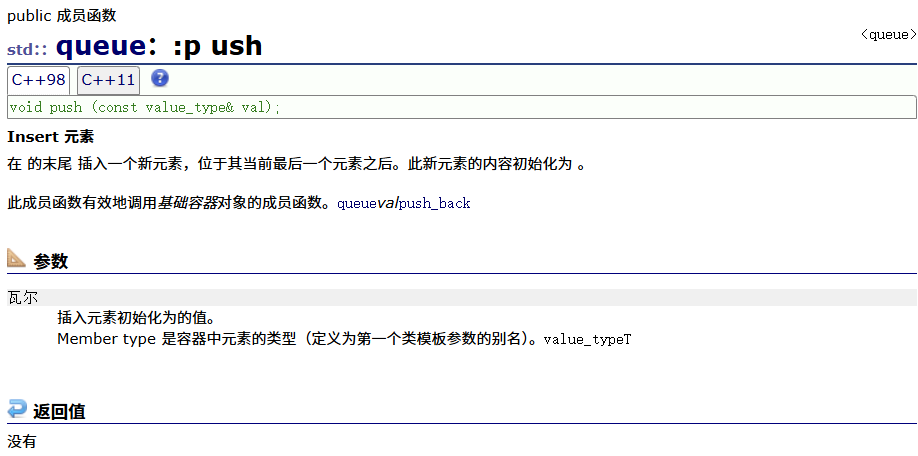
pop(出队列)
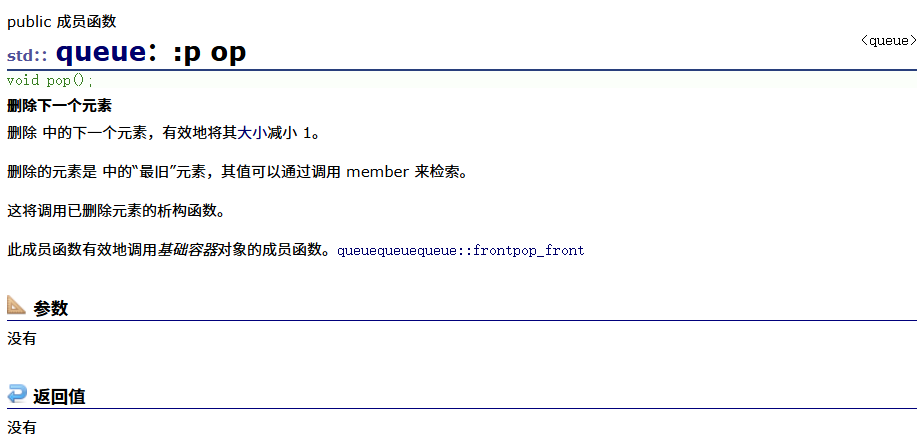
emplace
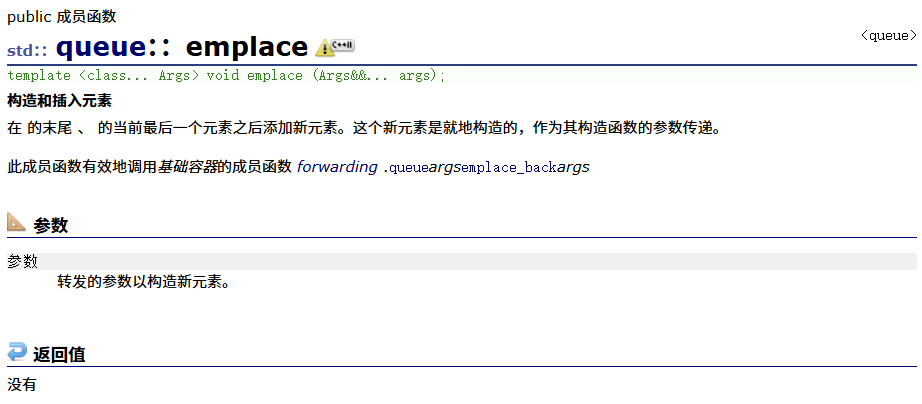 swap
swap
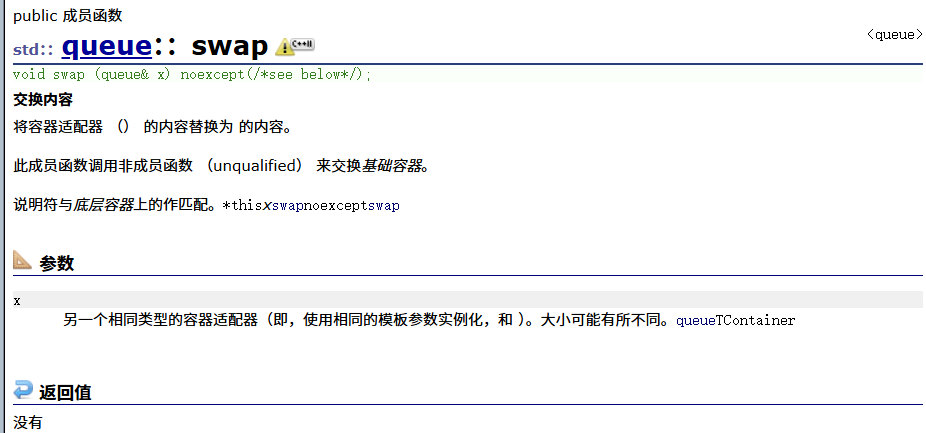
测试:
cpp
void test1()
{
queue<int> q;
q.push(1);
q.push(2);
q.push(3);
cout << q.front() << endl;
while (!q.empty())
{
cout << q.front() << " ";
q.pop();
}
cout << endl;
}
int main()
{
test1();
return 0;
}答案:
queue的模拟实现
cpp
#pragma once
#include <iostream>
#include<vector>
#include<list>
#include<deque>
using namespace std;
namespace Boogiepop
{
//适配器/配接器 //用缺省值可以不传递第二个模板参数
template<class T, class container = deque<T>>
//适配器是用来实现转换的
//本质上是容器适配器
//用容器适配转换出来的
class queue
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
//_con.erase(_con.begin());效率比较低
_con.pop_front();
}
size_t size() const
{
return _con.size();
}
bool empty() const
{
return _con.empty();
}
const T& top() const
{
return _con.back();
}
private:
container _con;
};
}deque的介绍和官方文档
官方文档:deque - C++ 参考
std::d eque - cppreference.com
deque(双端队列)的介绍

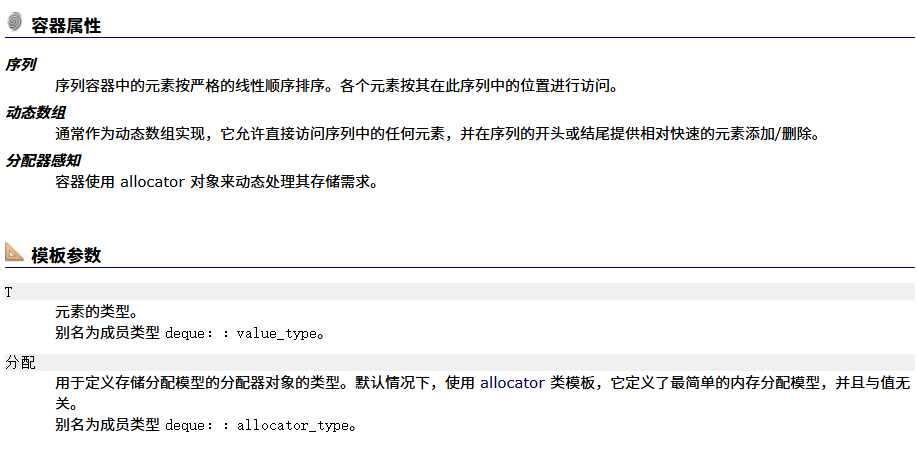
deque的结构图
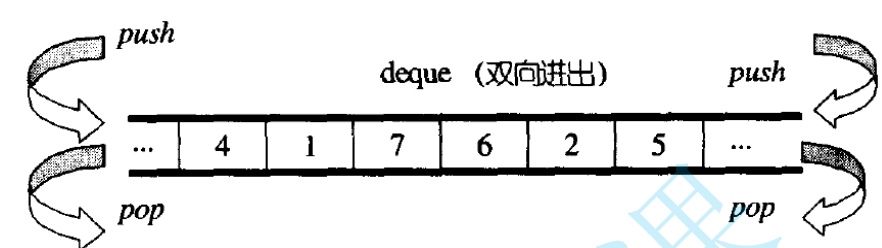
deque的特殊之处:为什么模拟实现用deque

如上图所示,deque在功能上拥有vector和list的结合。
但是deque遍历的性能并不高效
vector
优点:
1下标随机访问,快;
2尾插尾删效率高
3、CPU高速缓存命中率高
缺点:
1头部、中间插入删除效率低下;
2插入空间不够要扩容,扩容有一定性能消耗,倍数扩容有一定空间浪费
list
优点:
1、任意位置均为O(1)复杂度的插入删除
2、按需申请释放内存
缺点:
1、不支持下标随机访问
2、CPU高速缓存命中率低,还存在缓存污染。
deque
优点:适合头尾插入删除,效率高;下标随机访问效率还不错(大量数据处理不如vector)
缺点:中间位置插入删除效率低,需要大量挪动数据。
相比于vector和list,性能都不够极致
\]下标随机访问的效率:
list\<\