2.2 向量的基
2.2.1 标准基
在二维向量空间里有两个非常特殊的向量:
<math xmlns="http://www.w3.org/1998/Math/MathML"> i = [ 1 0 ] j = [ 0 1 ] \mathbf{i} =\begin{bmatrix}1 \\0 \end{bmatrix}\qquad \mathbf{j} =\begin{bmatrix}0 \\1\end{bmatrix} </math>i=[10]j=[01]
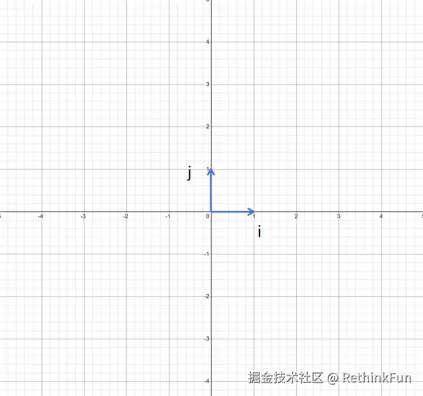
这两个向量分别沿x轴长度为1,沿y轴长度为1,互相垂直。
有了这两个向量,可以对其他向量有一个新的理解方式。也就是一个二维向量里的第一个分量是对i 向量的缩放,第二个分量是对j 向量的缩放。然后将缩放后的向量加起来就是这个向量。也就是说不把向量里的数字看成坐标,而是看成对i 和j 向量的缩放。比如对于如下向量 a。
<math xmlns="http://www.w3.org/1998/Math/MathML"> a = [ 3 2 ] \mathbf{a} =\begin{bmatrix}3 \\2 \end{bmatrix} </math>a=[32]
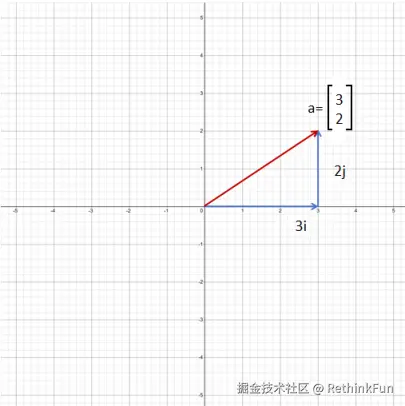
它可以看做是对 i 向量缩放3倍,对 j 向量缩放2倍,然后加和组成的向量。
通过对向量 i 和 j 进行线性运算,也就是进行数乘和向量加法,你可以得到二维向量空间里的任何一个向量。向量 i 和 j 可以作为构成其他向量的一个基础。所以称为二维空间的一组"基"。而且因为它们两个向量比较特殊,只在一个坐标轴上有值,而且值为1,彼此互相垂直,所以称为标准基 。二维空间标准基里的两个向量一般用 i 和 j 表示。
2.2.2 一般基
你还可以定义一些非标准的基,比如你可以用下边两个向量 a 和 b 来定义一个基。
<math xmlns="http://www.w3.org/1998/Math/MathML"> a = [ 2 1 ] b = [ − 1 1 ] \mathbf{a} =\begin{bmatrix}2 \\1 \end{bmatrix}\qquad \mathbf{b} =\begin{bmatrix}-1 \\1\end{bmatrix} </math>a=[21]b=[−11]
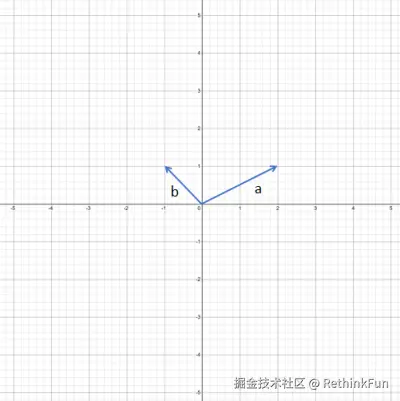
通过观察,不难发现,通过对 a 和 b 的缩放和加和,也是可以到达二维平面的任意一个点的。
通过一组向量的线性组合,可以到达的向量空间,叫做它们"张"成的空间。单位向量 i 和 j ,还有上边定义的向量 a 和 b 张成的空间都是整个二维空间。
2.2.3 线性相关
我们再看下边这一组向量:
<math xmlns="http://www.w3.org/1998/Math/MathML"> a = [ 2 2 ] b = [ 1 1 ] \mathbf{a} =\begin{bmatrix}2 \\2 \end{bmatrix}\qquad \mathbf{b} =\begin{bmatrix}1 \\1\end{bmatrix} </math>a=[22]b=[11]

它们两个向量在同一个直线上,它们两个任意线性组合,也就是通过数乘缩放和向量相加,所能生成的向量还在这条直线上。也就是这两个向量张成的空间就是这条直线。此时,这两个向量就不能构成一个基。因为他们线性相关。
线性相关:如果一组向量里至少有一个向量可以表示为其他向量的线性组合,那么就称这一组向量线性相关。
比如上边的向量 a 就可以用 b 缩放2倍获得,所以它们两个是线性相关的。
2.2.4基的定义
下边我们给出基的定义:
基:向量空间的一组基是指张成该空间的一个线性无关的向量组。
有了基的定义,每个向量里的分量都可以看成对基里边对应向量的缩放,然后加和得到的向量。一般不做说明,都是对标准基进行缩放和加和。
2.2.5更高维度的基
三维向量的标准基里的向量一般用 i ,j ,k 向量来表示。他们分别位于 x,y,z 轴上,长度为1,彼此垂直。
<math xmlns="http://www.w3.org/1998/Math/MathML"> i = [ 1 0 0 ] j = [ 0 1 0 ] k = [ 0 0 1 ] \mathbf{i} =\begin{bmatrix}1 \\0 \\0\end{bmatrix}\qquad \mathbf{j} =\begin{bmatrix}0 \\1\\0\end{bmatrix}\qquad \mathbf{k} =\begin{bmatrix}0 \\0\\1\end{bmatrix} </math>i= 100 j= 010 k= 001
下边的向量,可以看做对 i 缩放2倍,对 j 缩放8倍,对 k 缩放7倍,再相加得到。
<math xmlns="http://www.w3.org/1998/Math/MathML"> x = [ 2 8 7 ] \mathbf{x} =\begin{bmatrix}2 \\8 \\7\end{bmatrix} </math>x= 287
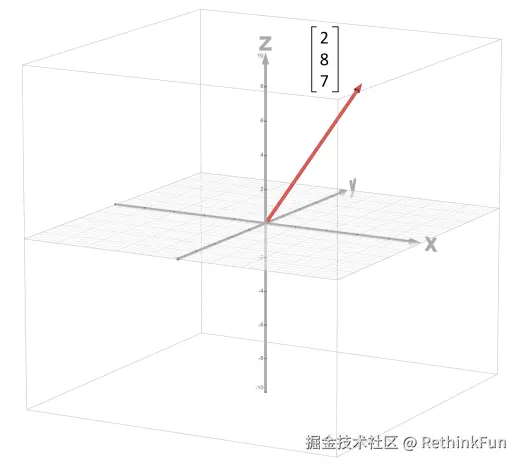
三维空间里的3个向量可以张成的空间有哪些呢?

最大可能是张成整个三维空间。

其次,如果三个向量里的其中一个可以通过另外两个线性组合得到,也就是位于另外两个向量张成平面里,那么它们三个向量张成的空间就是一个面。

还有一种情况,就是三个向量里的两个向量,都可以通过第三个向量经过缩放得到,也就是两个向量都处于第三个向量张成的线上,那么它们三个向量张成的空间就是一条直线。

最后一种情况,就是三个向量都是0向量,也就是向量的各个分量都是0,那么它们张成的空间就是一个点,零点。
三维空间里的2个向量可以张成的空间包含哪些呢?
不难想象,可以是一个面,一条直线,或者零点。
这种思想你可以延伸到 n 维空间,n 维空间也有自己的标准基,标准基里的向量分别位于不同的轴线上,长度为1,彼此垂直。n 维空间也有非标准基。n 维空间里的m (m小于等于n)个向量张成的空间维度小于等于m。
这个教程我也会同步在B站更新视频教程。欢迎大家在B站搜索RethinkFun观看。