数据结构与算法之美：拓扑排序

Hello大家好！很高兴我们又见面啦！给生活添点passion，开始今天的编程之路！

我的博客： <但凡.

我的专栏： 《编程之路》、《数据结构与算法之美》、《C++修炼之路》、《Linux修炼：终端之内洞悉真理》

感谢你打开这篇博客！希望这篇博客能为你带来帮助，也欢迎一起交流探讨，共同成长。

拓扑排序其实是图相关的内容，但是当时我忘了这一部分了，所以单独拿一篇文章来补充上。

1、拓扑排序概述

1、拓扑排序概述

拓扑排序是对有向无环图（DAG）的顶点进行线性排序，使得对于图中的每一条有向边 (u, v)，顶点 u 在排序中总是位于顶点 v 的前面。常用于任务调度、依赖解析等场景。

简单来说，拓扑排序就是每次从入度为0的点开始，每次都走入度为0的点，直到遍历完所有的顶点。拓扑排序只适用于有向无环图，并且，拓扑排序的结果可能不唯一。

2、拓扑排序的实现

基于邻接表的实现

以下是使用邻接表和深度优先搜索（DFS）的C++实现：

cpp 复制代码

#include <iostream>
#include <vector>
#include <stack>
#include <list>
using namespace std;

class Graph {
    int V; // 顶点数
    list<int>* adj; // 邻接表
    void topologicalSortUtil(int v, bool visited[], stack<int>& Stack);

public:
    Graph(int V);
    void addEdge(int v, int w);
    void topologicalSort();
};

Graph::Graph(int V) {
    this->V = V;
    adj = new list<int>[V];
}

void Graph::addEdge(int v, int w) {
    adj[v].push_back(w); // 添加边v->w
}

void Graph::topologicalSortUtil(int v, bool visited[], stack<int>& Stack) {
    visited[v] = true;
    for (auto i = adj[v].begin(); i != adj[v].end(); ++i)
        if (!visited[*i])
            topologicalSortUtil(*i, visited, Stack);
    Stack.push(v);
}

void Graph::topologicalSort() {
    stack<int> Stack;
    bool* visited = new bool[V];
    for (int i = 0; i < V; i++)
        visited[i] = false;

    for (int i = 0; i < V; i++)
        if (!visited[i])
            topologicalSortUtil(i, visited, Stack);

    while (!Stack.empty()) {
        cout << Stack.top() << " ";
        Stack.pop();
    }
}

int main() {
    Graph g(6);
    g.addEdge(5, 2);
    g.addEdge(5, 0);
    g.addEdge(4, 0);
    g.addEdge(4, 1);
    g.addEdge(2, 3);
    g.addEdge(3, 1);

    cout << "拓扑排序结果: ";
    g.topologicalSort();
    return 0;
}

我们来分析以下上面的算法，其实关于dfs，还是那句"一条路走到黑"来概括更为合适。我们在只要遍历到入度为0的点，就以这个点为起点开始dfs，在dfs过程中遇到的所有点都先加入栈，最后，再依次弹出栈。光说不好理解，我们看图来理解一下：

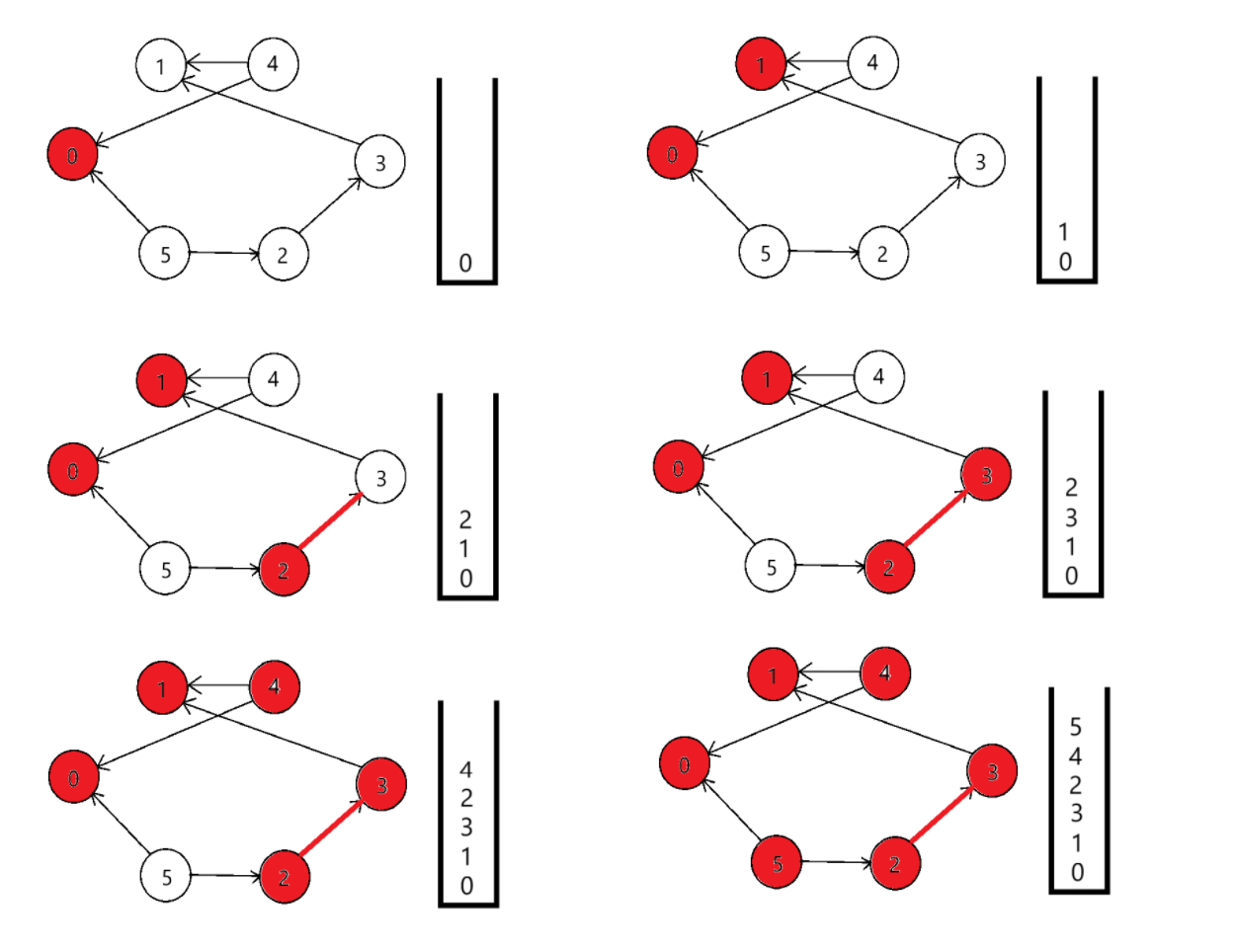
最后再依次出栈，就是拓扑排序。

Kahn算法实现（基于入度）

其实一般提到拓扑排序，都是基于Kahn算法实现的。Kahn算法通过维护入度表实现拓扑排序，步骤如下：

cpp 复制代码

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

vector<int> topologicalSort(int V, vector<vector<int>>& adj) {
    vector<int> inDegree(V, 0);
    queue<int> q;
    vector<int> result;

    // 计算每个顶点的入度
    for (int u = 0; u < V; u++)
        for (int v : adj[u])
            inDegree[v]++;

    // 入度为0的顶点入队
    for (int i = 0; i < V; i++)
        if (inDegree[i] == 0) q.push(i);

    while (!q.empty()) {
        int u = q.front();
        q.pop();
        result.push_back(u);

        for (int v : adj[u])
            if (--inDegree[v] == 0)
                q.push(v);
    }

    if (result.size() != V) {
        cout << "图中存在环！" << endl;
        return {};
    }
    return result;
}

int main() {
    int V = 6;
    vector<vector<int>> adj(V);
    adj[5] = {2, 0};
    adj[4] = {0, 1};
    adj[2] = {3};
    adj[3] = {1};

    vector<int> sorted = topologicalSort(V, adj);
    for (int v : sorted) cout << v << " ";
    return 0;
}

我们还是根据图来理解一下：

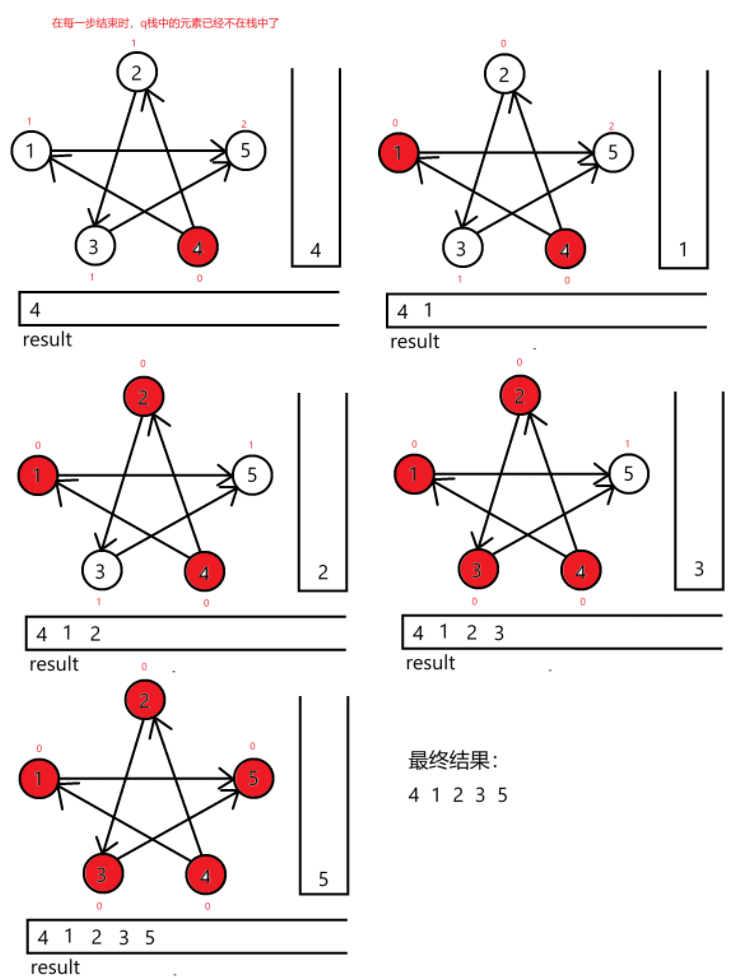
关键注意事项

两种方法时间复杂度均为 O(V+E)，其中V为顶点数，E为边数
DFS实现的结果是逆序的，需要通过栈反转输出
Kahn算法可以直接检测图中是否存在环（当结果集大小不等于顶点数时）

3、应用场景扩展

拓扑排序可应用于：

编译器中的指令调度
软件包依赖管理（如apt-get/yum）
课程选修顺序规划
任务调度系统

两种实现方式各有优劣：DFS代码简洁但需要额外空间存储栈；Kahn算法更直观且能直接检测环，但需要维护入度表。根据具体场景选择合适实现。但是我个人认为还是Kahn算法更好想一些。

好了，今天的内容就分享到这，我们下期再见！