数组和特殊矩阵
数组
数组的定义
数组 是由n(n>=1)个相同类型的数据元素构成的有限序列。每个数据元素称为一个数组元素 ,每个元素在n个线性关系中的序号称之为该元素的下标 ,下标的取值范围称为数组的维界。
数组是[[线性表]]的推广,一维数组可视为一个线性表,二维数组可视为其元素是定长数组的线性表。
数组的存储结构
各数组元素大小相同,且物理上连续存放。
我们用一个 Markdown 表格模拟数组的地址存储结构(ElemType a[7]):
| 其他 | a[0] | a[1] | a[2] | a[3] | a[4] | a[5] | a[6] | 其他 |
|---|---|---|---|---|---|---|---|---|
| LOC | LOC+1 | ... | ... | ... | ... | ... | ... |
数组元素a[i]的存放地址=LOC+i∗sizeof(ElemType) 数组元素a[i]的存放地址= LOC + i * sizeof(ElemType) 数组元素a[i]的存放地址=LOC+i∗sizeof(ElemType)
每个单元格表示数组元素在内存中的连续存储位置,数组元素之间没有间隔,便于通过下标快速访问。
接下来假设有一个二维数组() ElemType b[2][4],我们可以用一个 Markdown 表格模拟其地址存储结构和逻辑结构:
逻辑结构:
| b[0][0] | b[0][1] | b[0][2] | b[0][3] |
|---|---|---|---|
| b[1][0] | b[1][1] | b[1][2] | b[1][3] |
但是在内存中,数组是连续的,那么也就有了行优先和列优先的存储方式。
列优先存储结构:
| 其他 | b[0][0] | b[1][0] | b[0][1] | b[1][1] | b[0][2] | b[1][2] | b[0][3] | b[1][3] | 其他 |
|---|---|---|---|---|---|---|---|---|---|
| ... | LOC+0 | LOC+1 | LOC+2 | LOC+3 | LOC+4 | LOC+5 | LOC+6 | LOC+7 | ... |
M行N列的二维数组b[M][N]中,若按列优先存储,则:
b[i][j]的存放地址=LOC+(j∗M+i)∗sizeof(ElemType) b[i][j]的存放地址= LOC + (j * M + i) * sizeof(ElemType) b[i][j]的存放地址=LOC+(j∗M+i)∗sizeof(ElemType)
行优先存储结构:
| 其他 | b[0][0] | b[0][1] | b[0][2] | b[0][3] | b[1][0] | b[1][1] | b[1][2] | b[1][3] | 其他 |
|---|---|---|---|---|---|---|---|---|---|
| ... | LOC+0 | LOC+1 | LOC+2 | LOC+3 | LOC+4 | LOC+5 | LOC+6 | LOC+7 | ... |
M行N列的二维数组b[M][N]中,若按行优先存储,则:
b[i][j]的存放地址=LOC+(i∗N+j)∗sizeof(ElemType) b[i][j]的存放地址= LOC + (i * N + j) * sizeof(ElemType) b[i][j]的存放地址=LOC+(i∗N+j)∗sizeof(ElemType)
矩阵的存储和特殊矩阵的压缩存储
压缩存储 是指为多个值相同的元素只分配一个存储空间,对零元素不分配空间。
特殊矩阵 就是指分布有一定规律的矩阵。
压缩存储方法:找出分布规律,把那些呈现规律性分布的、值相同的元素放在同一个存储空间中。
对称矩阵
| a1,1a_{1,1}a1,1 | a1,2a_{1,2}a1,2 | ⋯\cdots⋯ | a1,na_{1,n}a1,n |
|---|---|---|---|
| a2,1a_{2,1}a2,1 | a2,2a_{2,2}a2,2 | ⋯\cdots⋯ | a2,na_{2,n}a2,n |
| ⋮\vdots⋮ | ⋮\vdots⋮ | ⋱\ddots⋱ | ⋮\vdots⋮ |
| an,1a_{n,1}an,1 | an,2a_{n,2}an,2 | ⋯\cdots⋯ | an,na_{n,n}an,n |
如上所示的矩阵是一个n阶矩阵,若对于任意的i,ji,ji,j,都有ai,j=aj,ia_{i,j}=a_{j,i}ai,j=aj,i,则称之为对称矩阵 。其中的元素也可以根据i,j的大小分为三个部门:i=ji=ji=j主对角线,i>ji>ji>j 下三角区,i<ji<ji<j 上三角区。
普通存储:n*n二维数组,因为上下两个三角区数值相同,所以可以压缩存储。
压缩存储策略:只存储主对角线+下三角区(或主对角线+上三角区)
同时我们需要按照行/列优先的原则存入到一个一维数组中,并建立i,j(矩阵下标)与数组下标的映射关系。
以下以行优先为例:
对于i>=j的下标来说,第一个存储的是 i=1,j=1,第二个存储的是 i=2,j=1,接着 2,2、3,1、3,2、3,3。分别映射到了0,1,2,3上面。
根据不难看出,对于i是累加的,比如第一行起始是0,第二行起始是1,到了第三行起始就变为了3。那么其实他就是一个等差数列。
根据等差数列求和公式:n(a1+an)2\frac{n(a_1 + a_n)}{2}2n(a1+an),其中a1=0a_1 = 0a1=0,an=i−1a_n = i - 1an=i−1,n=in = in=i。因此,第iii行的起始下标为i(i−1)2\frac{i(i-1)}{2}2i(i−1)。接着我们加上j的偏移量,得到下标为i(i−1)2+j−1\frac{i(i-1)}{2} + j - 12i(i−1)+j−1。(j-1的原因是因为数组下标从0开始)
至此我们把矩阵中下三角的元素都存储了,正因为ai,j=aj,ia_{i,j} = a_{j,i}ai,j=aj,i,对于上三角的元素,我们直接替换下标即可。
得到最终的下标转换公式如下:
k={(i−1)i2+j−1,当 i≥j(下三角区和主对角线元素)(j−1)j2+i−1,当 i<j(上三角区元素) k = \begin{cases} \frac{(i-1)i}{2} + j-1, & \text{当 } i \geq j \text{(下三角区和主对角线元素)} \\ \frac{(j-1)j}{2} + i-1, & \text{当 } i < j \text{(上三角区元素)} \end{cases} k={2(i−1)i+j−1,2(j−1)j+i−1,当 i≥j(下三角区和主对角线元素)当 i<j(上三角区元素)
按照上面的方法,分析列优先:
对于i>=j的下标来说,第一个存储的是 i=1,j=1,第二个存储的是 i=1,j=2,接着 2,2、1,3、2,3、3,3。分别映射到了0,1,2,3上面。
根据等差数列求和公式:n(a1+an)2\frac{n(a_1 + a_n)}{2}2n(a1+an),其中a1=0a_1 = 0a1=0,an=j−1a_n = j - 1an=j−1,n=jn = jn=j。因此,第jjj列的起始下标为j(j−1)2\frac{j(j-1)}{2}2j(j−1)。接着我们加上i的偏移量,得到下标为j(j−1)2+i−1\frac{j(j-1)}{2} + i - 12j(j−1)+i−1。(i-1的原因是因为数组下标从0开始)
至此,我们得到列优先的公式为:
k={j(j−1)2+i−1,if i≥ji(i−1)2+j−1,if i<j k = \begin{cases} \frac{j(j-1)}{2} + i - 1, & \text{if } i \geq j \\ \frac{i(i-1)}{2} + j - 1, & \text{if } i < j \end{cases} k={2j(j−1)+i−1,2i(i−1)+j−1,if i≥jif i<j
对于存储上三角的方法,我不想写了,留给我自己思考去吧
三角矩阵
| a1,1a_{1,1}a1,1 | CCC | CCC | CCC |
|---|---|---|---|
| a2,1a_{2,1}a2,1 | a2,2a_{2,2}a2,2 | CCC | CCC |
| a3,1a_{3,1}a3,1 | a3,2a_{3,2}a3,2 | a3,3a_{3,3}a3,3 | CCC |
| a4,1a_{4,1}a4,1 | a4,2a_{4,2}a4,2 | a4,3a_{4,3}a4,3 | a4,4a_{4,4}a4,4 |
下三角矩阵:除了主对角线和下三角区,其余的元素都相同(如表格所示)
上三角矩阵:除了主对角线和上三角区,其余的元素都相同(如表格所示)
压缩存储策略 (下三角矩阵为例):按行优先原则将下三角区存入一维数组中。并在最后一个位置存储常量C,上面分析的下三角区存储公式可以直接使用。而常数C的存储位置为n(n+1)/2n(n+1)/2n(n+1)/2
存储下三角矩阵的下标转换公式:
k={(i−1)i2+j−1, if i≥j(下三角区和主对角线元素)n(n+1)2,if i<j(上三角区元素) k = \begin{cases} \frac{(i-1)i}{2} + j - 1, & \ \text{if } i \geq j (下三角区和主对角线元素) \\ \frac{n(n+1)}{2}, & \text{if } i < j (上三角区元素) \end{cases} k={2(i−1)i+j−1,2n(n+1), if i≥j(下三角区和主对角线元素)if i<j(上三角区元素)
下面开始分析上三角矩阵的存储,还是上面的策略,常数C的存储位置为n(n+1)/2n(n+1)/2n(n+1)/2。
那么对于第i行应当开始存储的位置应该为上i-1行的元素个数,应当为n(i−1)−(i−1)(i−2)2=(i−1)(2n−i+2)2n(i-1)-\frac{(i-1)(i-2)}{2}=\frac{(i-1)(2n-i+2)}{2}n(i−1)−2(i−1)(i−2)=2(i−1)(2n−i+2),其中,n(i−1)n(i-1)n(i−1)代表该矩阵第i行之前一共的元素数目,之后的式子代表下三角区的累计数目,对于第j列,应为相对于对角线的偏移量即为(j-i)。
因此我们可以得到存储上三角矩阵的下标转换公式:
k={(i−1)(2n−i+2)2+(j−i)i≤j(上三角区和主对角线元素)n(n+1)2i>j(下三角区元素) k = \begin{cases} \frac{(i-1)(2n-i+2)}{2} + (j-i) & i \leq j (上三角区和主对角线元素) \\ \frac{n(n+1)}{2} & i > j (下三角区元素) \end{cases} k={2(i−1)(2n−i+2)+(j−i)2n(n+1)i≤j(上三角区和主对角线元素)i>j(下三角区元素)
三对角矩阵
三对角矩阵,又称带状矩阵:当∣i−j∣>1|i-j|>1∣i−j∣>1时,元素值为0。(1≤i,j≤n)(1\leq i,j\leq n)(1≤i,j≤n)
| a1,1a_{1,1}a1,1 | a1,2a_{1,2}a1,2 | 0 | 0 | 0 | 0 |
|---|---|---|---|---|---|
| a2,1a_{2,1}a2,1 | a2,2a_{2,2}a2,2 | a2,3a_{2,3}a2,3 | 0 | 0 | 0 |
| 0 | a3,2a_{3,2}a3,2 | a3,3a_{3,3}a3,3 | a3,4a_{3,4}a3,4 | 0 | 0 |
| 0 | 0 | a4,3a_{4,3}a4,3 | a4,4a_{4,4}a4,4 | a4,5a_{4,5}a4,5 | 0 |
| 0 | 0 | 0 | a5,4a_{5,4}a5,4 | a5,5a_{5,5}a5,5 | a5,6a_{5,6}a5,6 |
| 0 | 0 | 0 | 0 | a6,5a_{6,5}a6,5 | a6,6a_{6,6}a6,6 |
压缩存储策略:按行优先(或列优先)原则,只存储带状部分
那么按行优先规则,前i-1行的元素个数为3(i−1)−13(i-1)-13(i−1)−1,第i行的元素个数为3,最后一行的元素个数为2。那么ai,ja_{i,j}ai,j是第i行的第j-i+2(如果下标从1开始,从零开始还要减1)个元素。所以我们得到如下的公式:
k=3(i−1)−1+j−i+2−1=2i+j−3 k=3(i-1)-1+j-i+2-1=2i+j-3 k=3(i−1)−1+j−i+2−1=2i+j−3
接下来我们需要讨论一下逆向,即通过k求i和j:
由一维数组下标 kkk 求矩阵下标 i,ji, ji,j 的方法如下:首先确定行号 iii,由于前 i−1i-1i−1 行共 3(i−1)−13(i-1)-13(i−1)−1 个元素,前 iii 行共 3i−13i-13i−1 个元素,因此有 3(i−1)−1<k+1≤3i−13(i-1)-1 < k+1 \leq 3i-13(i−1)−1<k+1≤3i−1,即 i≥k+23i \geq \frac{k+2}{3}i≥3k+2,向上取整得 i=⌈k+23⌉i = \lceil \frac{k+2}{3} \rceili=⌈3k+2⌉。
也可以按照王道书的逻辑,3(i−1)−1≤k<3i−13(i-1)-1 \leq k < 3i-13(i−1)−1≤k<3i−1,即 i≤k+13+1i \leq \frac{k+1}{3} + 1i≤3k+1+1,向下取整得 i=⌊k+13⌋+1i = \lfloor \frac{k+1}{3} \rfloor + 1i=⌊3k+1⌋+1。确定 iii 后,前 i−1i-1i−1 行共 3(i−1)−13(i-1)-13(i−1)−1 个元素,第 iii 行的第一个元素下标为 k0=3(i−1)−1k_0 = 3(i-1)-1k0=3(i−1)−1,所以列号 j=k−k0−2+ij = k - k_0 - 2 + ij=k−k0−2+i。公式总结如下:
i=⌈k+23⌉j=k−[3(i−1)−1]−2+i \begin{aligned} &i = \lceil \frac{k+2}{3} \rceil \\ &j = k - [3(i-1)-1] - 2 + i \end{aligned} i=⌈3k+2⌉j=k−[3(i−1)−1]−2+i
或者
i=⌊k+13⌋+1j=k−[3(i−1)−1]−2+i \begin{aligned} &i = \lfloor \frac{k+1}{3} \rfloor + 1 \\ &j = k - [3(i-1)-1] - 2 + i \end{aligned} i=⌊3k+1⌋+1j=k−[3(i−1)−1]−2+i
先根据 kkk 计算 iii,再用 iii 计算 jjj,两种取整方式结果一致。
稀疏矩阵
稀疏矩阵:非零元素远远少于矩阵元素的个数
压缩存储策略:顺序存储------三元组<行,列,值>
例如,下面的稀疏矩阵:
| 0 | 0 | 4 | 0 | 0 | 5 |
|---|---|---|---|---|---|
| 0 | 3 | 0 | 9 | 0 | 0 |
| 0 | 0 | 0 | 0 | 7 | 0 |
| 0 | 2 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 |
其三元组顺序存储形式为:(行、列标从0开始)
| i行 | j列 | v值 |
|---|---|---|
| 0 | 2 | 4 |
| 0 | 5 | 5 |
| 1 | 1 | 3 |
| 1 | 3 | 9 |
| 2 | 4 | 7 |
| 3 | 1 | 2 |
行、列标从1开始
| 行 | 列 | 值 |
|---|---|---|
| 1 | 3 | 4 |
| 1 | 6 | 5 |
| 2 | 2 | 3 |
| 2 | 4 | 9 |
| 3 | 5 | 7 |
| 4 | 2 | 2 |
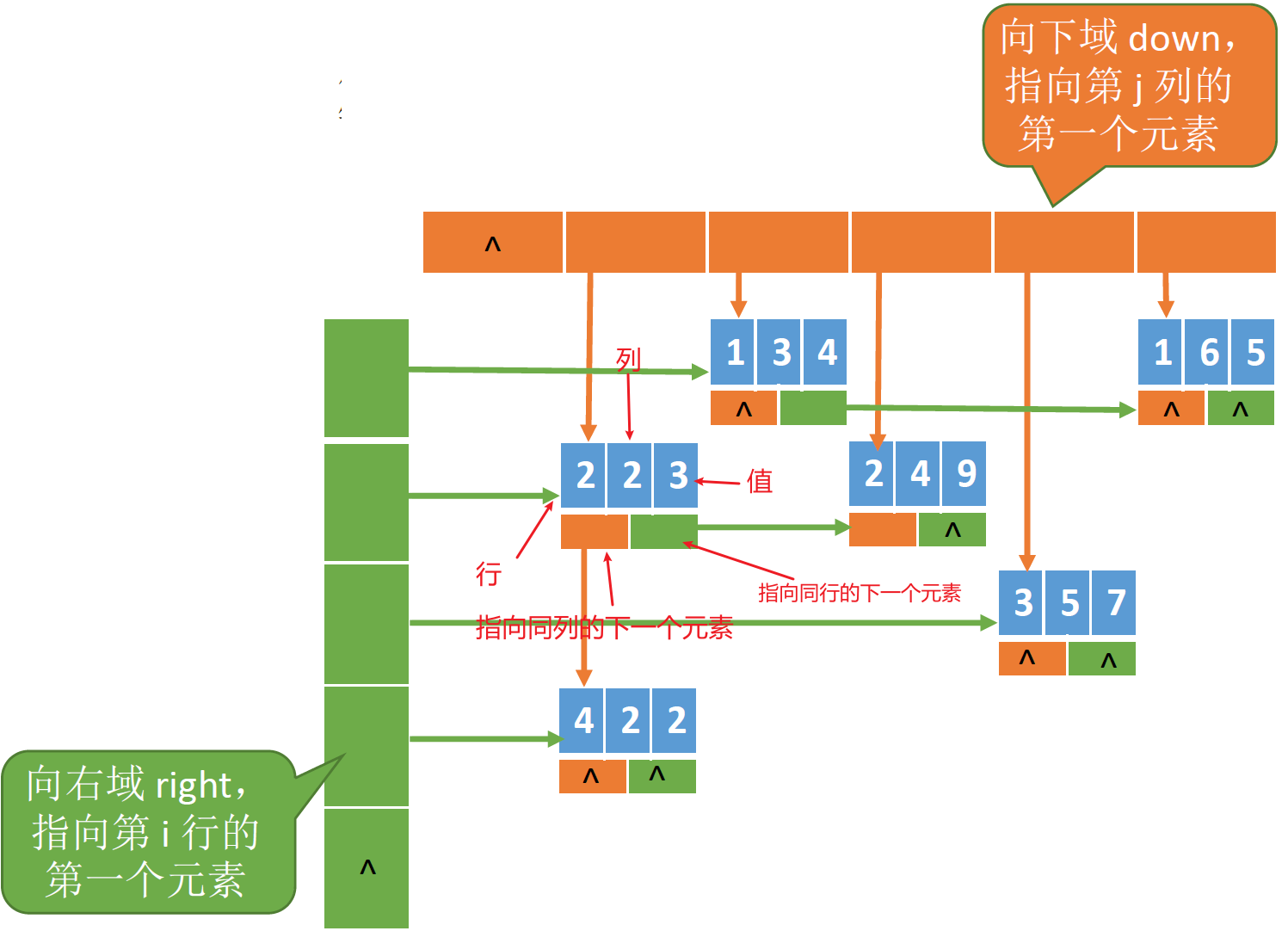
既然有顺序存储,那么会有链式存储的方式。压缩存储策略二:链式存储------十字链表法
一个结点包含五部分内容:行、列、值、指向下一个同列元素的指针、指向下一个同行元素的指针。
还是上面的矩阵,如果给他创建一个十字链表,那么就会得到如下结果(图源王道课PPT):