在计算机视觉中,相机标定是非常重要的一步,主要目的是从图像中恢复出物体的三维信息。为了做到这一点,我们需要了解和使用一系列的数学工具,这些工具描述了相机的成像过程,包括相机的内参、外参、畸变系数、投影矩阵和矫正矩阵。
本文主要讲解相机参数的格式与作用,相机标定可参考这篇博文相机标定
一、相机内参(Camera Intrinsics)
1.1 内参的定义
相机内参指的是描述相机光学成像系统内部几何关系的参数。它主要涉及如何将三维空间中的点投影到二维图像平面。具体来说,相机内参矩阵包含了相机的焦距、主点以及畸变系数等信息。
1.2 内参矩阵的固定格式
在进行开发时相机内参一般用如下格式表示cameraMatrix
cv::Mat_<double>(3, 3)
内参矩阵通常采用3x3的矩阵表示,格式如下:
K = [ f x s c x 0 f y c y 0 0 1 ] K = \begin{bmatrix} f_x & s & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} K= fx00sfy0cxcy1
其中:
- f x f_x fx 和 f y f_y fy 分别是相机在x和y方向的焦距,单位为像素,这两个参数反映了图像传感器上每毫米对应的像素数量。通常情况下,焦距在水平方向和垂直方向可能不相等。
- c x c_x cx 和 c y c_y cy 是图像的主点坐标,通常是图像的中心点。如果图像的分辨率为 W × H W \times H W×H,那么 c x = W / 2 c_x = W/2 cx=W/2, c y = H / 2 c_y = H/2 cy=H/2。
- s s s 是切向畸变系数,通常在大部分相机中是零,除非相机镜头存在较严重的切向畸变。
该矩阵通过将三维世界坐标系中的点转换为图像坐标系中的点。
1.3 内参矩阵的作用
-
将三维坐标转化为二维坐标 :内参矩阵的作用就是将世界坐标系中的三维点 X , Y , Z X, Y, Z X,Y,Z 投影到相机的二维图像坐标系中。
-
校正畸变:内参矩阵中的一些参数,如焦距和主点,可以用来去畸变或者校正图像中的几何误差。
-
计算图像尺寸和焦距 :内参矩阵的 f x f_x fx 和 f y f_y fy 值可用于计算图像中物体的实际物理尺寸或距离。
二、相机畸变系数(Distortion Coefficients)
2.1 畸变的定义
相机的畸变主要由光学镜头的特性引起。最常见的畸变有两种:
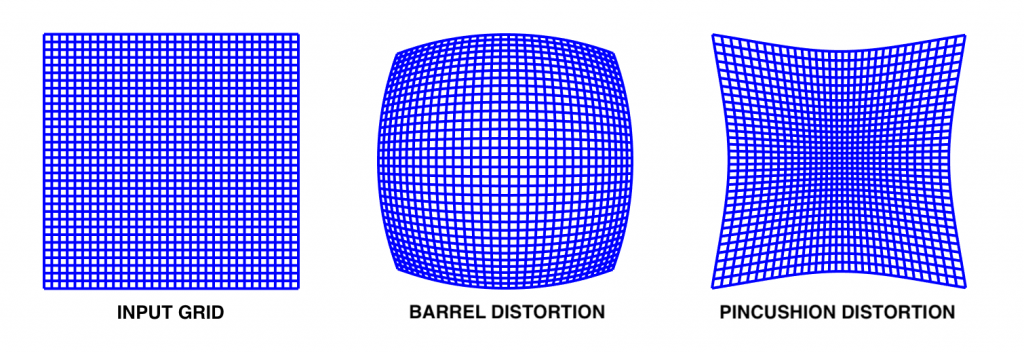
- 径向畸变:主要发生在图像的四周,造成图像的拉伸或压缩,通常表现为桶形畸变或枕形畸变。
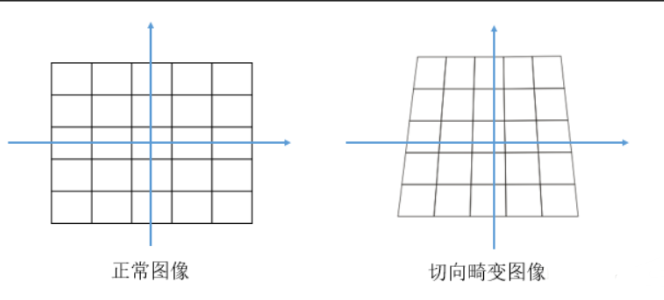
- 切向畸变 :通常是由相机镜头和图像平面之间的非理想对准引起的,表现为图像的倾斜或弯曲。
2.2 畸变系数的固定格式
开发中一般用如下代码表示distCoeffs
cv::Mat_<double>(1, 5)
在标准的针孔相机模型中,畸变系数由以下五个参数表示:
D = [ k 1 , k 2 , p 1 , p 2 , k 3 ] D = [k_1, k_2, p_1, p_2, k_3] D=[k1,k2,p1,p2,k3]
- k 1 , k 2 , k 3 k_1, k_2, k_3 k1,k2,k3 是径向畸变系数,描述图像的径向畸变。
- p 1 , p 2 p_1, p_2 p1,p2 是切向畸变系数,描述图像的切向畸变。
2.3 畸变系数的作用
- 径向畸变 :由镜头曲率导致,表现为"桶形畸变"(边缘像素向外偏移)或"枕形畸变"(边缘像素向内偏移),校正公式为:
x corrected = x ⋅ ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) , y corrected = y ⋅ ( 1 + k 1 r 2 + k 2 r 4 + k 3 r 6 ) x_{\text{corrected}} = x \cdot (1 + k_1 r^2 + k_2 r^4 + k_3 r^6), \quad y_{\text{corrected}} = y \cdot (1 + k_1 r^2 + k_2 r^4 + k_3 r^6) xcorrected=x⋅(1+k1r2+k2r4+k3r6),ycorrected=y⋅(1+k1r2+k2r4+k3r6)
其中 r 2 = x 2 + y 2 r^2 = x^2 + y^2 r2=x2+y2, k 1 、 k 2 、 k 3 k_1、k_2、k_3 k1、k2、k3为径向畸变系数。 - 切向畸变 :由镜头装配偏差导致,校正公式为:
x corrected = x + 2 p 1 x y + p 2 ( r 2 + 2 x 2 ) , y corrected = y + p 1 ( r 2 + 2 y 2 ) + 2 p 2 x y x_{\text{corrected}} = x + 2p_1 xy + p_2 (r^2 + 2x^2), \quad y_{\text{corrected}} = y + p_1 (r^2 + 2y^2) + 2p_2 xy xcorrected=x+2p1xy+p2(r2+2x2),ycorrected=y+p1(r2+2y2)+2p2xy
其中 p 1 、 p 2 p_1、p_2 p1、p2为切向畸变系数。
- 去畸变:畸变系数用于矫正图像中的畸变,特别是在使用广角镜头时,畸变非常明显。
- 提高计算机视觉算法的精度:去除畸变后,图像会更加接近真实的物理结构,进而提高目标识别、三维重建等算法的精度。
三、相机外参(Camera Extrinsics)
3.1 外参的定义
相机外参是描述相机与世界坐标系之间关系的参数。它通过旋转矩阵( R R R)和位移向量( T T T)来表示。旋转矩阵描述了相机坐标系与世界坐标系之间的旋转关系,而位移向量描述了两者之间的平移关系。
3.2 外参矩阵的格式
相机外参矩阵通常由一个 3 × 3 3 \times 3 3×3 的旋转矩阵 R R R 和一个 3 × 1 3 \times 1 3×1 的平移向量 T T T 组成。外参矩阵通常是一个 3 × 4 3 \times 4 3×4 的矩阵:
R ∣ T \] = \[ R 11 R 12 R 13 T x R 21 R 22 R 23 T y R 31 R 32 R 33 T z \] \[R \| T\] = \\begin{bmatrix} R_{11} \& R_{12} \& R_{13} \& T_x \\\\ R_{21} \& R_{22} \& R_{23} \& T_y \\\\ R_{31} \& R_{32} \& R_{33} \& T_z \\end{bmatrix} \[R∣T\]= R11R21R31R12R22R32R13R23R33TxTyTz 其中: * R R R 是一个 3 × 3 3 \\times 3 3×3 的旋转矩阵,表示相机坐标系相对于世界坐标系的旋转。 * T T T 是一个 3 × 1 3 \\times 1 3×1 的平移向量,表示相机坐标系原点相对于世界坐标系原点的平移。 ##### 3.3 外参矩阵的作用 1. **将世界坐标系的三维点转化为相机坐标系的三维点**:外参矩阵用于表示相机的位置和姿态,帮助我们将三维物体的坐标从世界坐标系转换到相机坐标系。 2. **多视角对齐**:在多视角计算中,相机的外参矩阵非常重要,尤其是在立体视觉和三维重建中,外参矩阵帮助我们理解相机之间的相对位置和角度。 *** ** * ** *** #### 四、投影矩阵(Projection Matrix) ##### 4.1 投影矩阵的定义 投影矩阵是将三维世界坐标系中的点转换为二维图像坐标系中的点的矩阵。它综合了相机的内参和外参信息,通过对三维点进行线性变换,将其投影到图像平面。 ##### 4.2 投影矩阵的格式 投影矩阵通常由内参矩阵 K K K 和外参矩阵 \[ R ∣ T \] \[R \| T\] \[R∣T\] 组成,形式如下: P = K \[ R ∣ T \] P = K \[R \| T\] P=K\[R∣T
其中:
- K K K 是内参矩阵,描述了相机的内部几何参数。
-
R ∣ T \] \[R \| T\] \[R∣T\] 是外参矩阵,描述了相机在世界坐标系中的旋转和平移。
4.3 投影矩阵的作用
-
三维点到二维图像点的映射 :投影矩阵能够将相机坐标系下的三维点 X , Y , Z X, Y, Z X,Y,Z 映射为图像平面上的二维点 x , y x, y x,y,并将这些点用于后续的图像处理、目标检测等任务。
-
计算视差和三维重建:在立体视觉和三维重建中,投影矩阵帮助我们从不同视角的图像中恢复物体的三维结构。
五、矫正矩阵(Rectification Matrix)
5.1 矫正矩阵的定义
矫正矩阵用于去除立体视觉系统中由于相机不同视角引起的几何误差。通常在立体匹配和深度估计中,矫正矩阵将左右图像对齐到相同的图像平面,消除由视角差异造成的几何失真。
5.2 矫正矩阵的格式
在立体相机系统中,左右相机的矫正矩阵由旋转矩阵 R 1 , R 2 R_1, R_2 R1,R2 和投影矩阵 P 1 , P 2 P_1, P_2 P1,P2 组成,用来调整图像,使得图像上的同名点在同一扫描线中。矫正矩阵的格式通常为:
R 1 ∣ T 1 \] = Rectification Matrix for the left camera \[R_1 \| T_1\] = \\text{Rectification Matrix for the left camera} \[R1∣T1\]=Rectification Matrix for the left camera \[ R 2 ∣ T 2 \] = Rectification Matrix for the right camera \[R_2 \| T_2\] = \\text{Rectification Matrix for the right camera} \[R2∣T2\]=Rectification Matrix for the right camera 5.3 矫正矩阵的作用 1. **去除视差误差**:矫正矩阵消除了由于相机视角差异引起的几何畸变,使得图像对齐,从而进行精确的视差计算。 2. **提高深度估计精度**:在深度估计过程中,矫正矩阵使得左右图像的对应点对齐,有助于提高深度图的精度。 *** ** * ** ***