光伏不确定性场景分析：从LHS场景生成到k-means场景削减

关键词: 拉丁超立方抽样；k-means聚类；光伏不确定性；主题: 采用LHS进行场景生成，k-means聚类进行场景削减，假设预测服从期望为 0，方差为2的正态分布

在光伏领域，由于光照、天气等因素的影响，光伏输出功率存在较大的不确定性。为了更好地对光伏系统进行规划和管理，我们需要一种有效的方法来处理这种不确定性。今天就来聊聊通过拉丁超立方抽样（LHS）进行场景生成，再利用k - means聚类进行场景削减的技术，这里假设光伏功率预测服从期望为0，方差为2的正态分布。

拉丁超立方抽样（LHS）进行场景生成

拉丁超立方抽样是一种高效的抽样方法，相比于传统的蒙特卡洛抽样，它能在较少的样本数量下获得更好的分布覆盖。在光伏不确定性场景生成中，我们可以利用它来生成一系列符合特定分布（这里是期望为0，方差为2的正态分布）的场景。

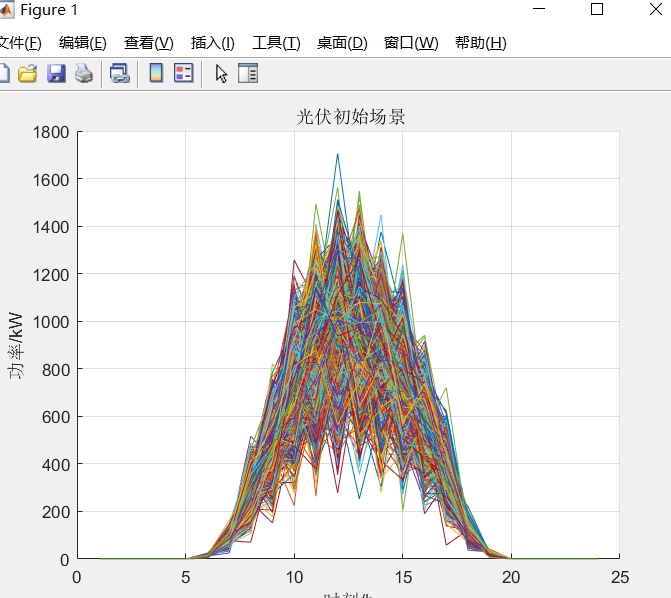
以下是一段Python代码示例：

python 复制代码

import numpy as np
from scipy.stats import norm


def lhs_sampling(n_samples, n_dimensions, mean=0, std_dev=np.sqrt(2)):
    samples = np.zeros((n_samples, n_dimensions))
    intervals = np.linspace(0, 1, n_samples + 1)
    for j in range(n_dimensions):
        u = np.random.uniform(size=n_samples)
        u.sort()
        u = (u + np.random.uniform(size=n_samples)) / 2.0
        samples[:, j] = norm.ppf((intervals[:n_samples] + u) / (n_samples), loc=mean, scale=std_dev)
    return samples


# 示例调用，生成100个样本，1个维度（可根据实际扩展维度）
scenarios = lhs_sampling(100, 1)

代码分析：

lhssampling**函数接受样本数量 n samples，维度数量 ndimensions*，以及分布的均值 mean 和标准差 std* dev（由于方差为2，这里标准差为sqrt(2)）作为参数。
intervals 划分了抽样的区间。
双重循环中，外层循环针对每个维度，内层循环对每个样本进行操作。首先生成均匀分布的随机数 u 并排序，然后通过特定的计算将其转换到合适的位置。
最后利用正态分布的百分点函数 norm.ppf 将均匀分布转换为符合我们期望的正态分布样本。

k - means聚类进行场景削减

生成的场景数量可能较多，不利于后续分析，这时就需要场景削减技术。k - means聚类是一种常用的无监督学习算法，可将相似的场景归为一类，从而削减场景数量。

以下是Python代码实现：

python 复制代码

from sklearn.cluster import KMeans


# 假设我们已经通过LHS得到了scenarios样本
k = 10  # 假设选择10个聚类中心，可根据实际调整
kmeans = KMeans(n_clusters=k, random_state=0).fit(scenarios)
reduced_scenarios = kmeans.cluster_centers_

代码分析：

首先导入 KMeans 类。
定义 k 为聚类中心的数量，这里设为10，这个值需要根据实际情况调整。如果 k 太小，可能会丢失重要信息；如果 k 太大，则达不到削减场景的目的。
使用 KMeans 类创建聚类模型，并调用 fit 方法对通过LHS生成的场景数据 scenarios 进行聚类。
聚类完成后，通过 clustercenters 属性获取聚类中心，这些聚类中心就可以作为削减后的场景，大大减少了场景数量，同时保留了原始场景的主要特征。

通过拉丁超立方抽样生成场景，再利用k - means聚类进行场景削减，我们能够有效地处理光伏不确定性带来的大量场景数据，为光伏系统的进一步分析和决策提供便利。这种方法在实际的光伏电站规划、电力系统调度等方面都有着重要的应用价值。