C++二叉搜索树

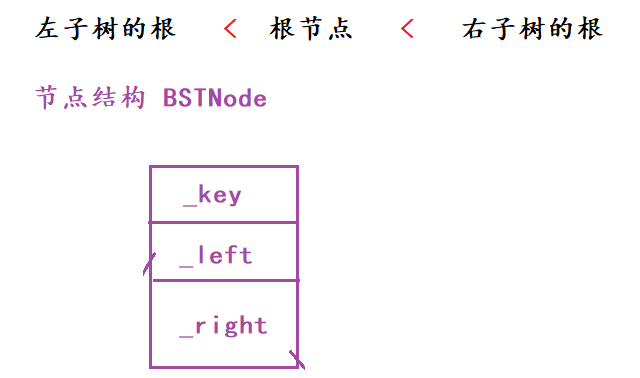
二叉搜索树（BinarySearchTree）是基于二叉树的一种数据结构。我们曾经接触过堆这种结构，堆的原理与此类似，但堆与二叉搜索树最大的区别是数据插入的逻辑！具体来说就是，堆分为大堆和小堆，我们按照大堆来解释，大堆要保证根节点大于子节点，若存在两个子节点则子节点的大小关系无具体要求限制。二叉搜索树则是对根、左子树、右子树做了明确的要求，对于一棵二叉搜索树，它的左子树<根节点<右子树

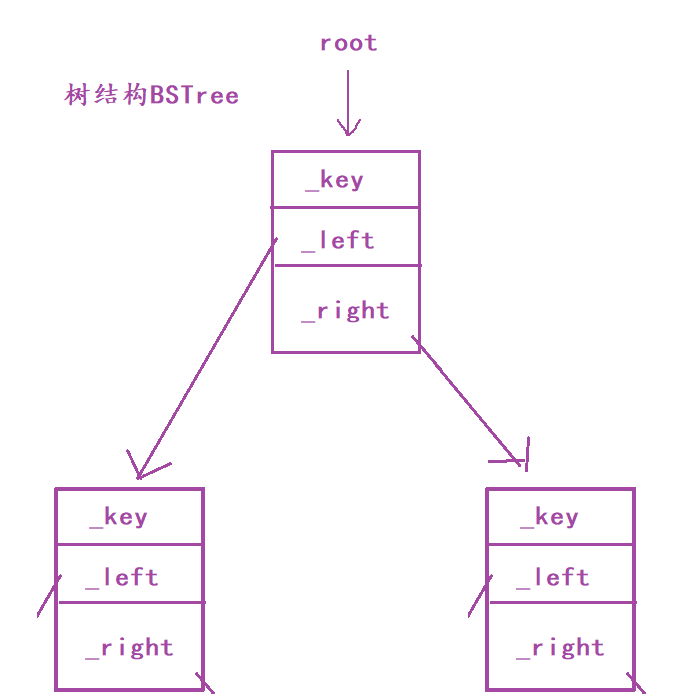
二叉搜索树的结构

节点的结构

二叉搜索树的结构

二叉树接口的实现

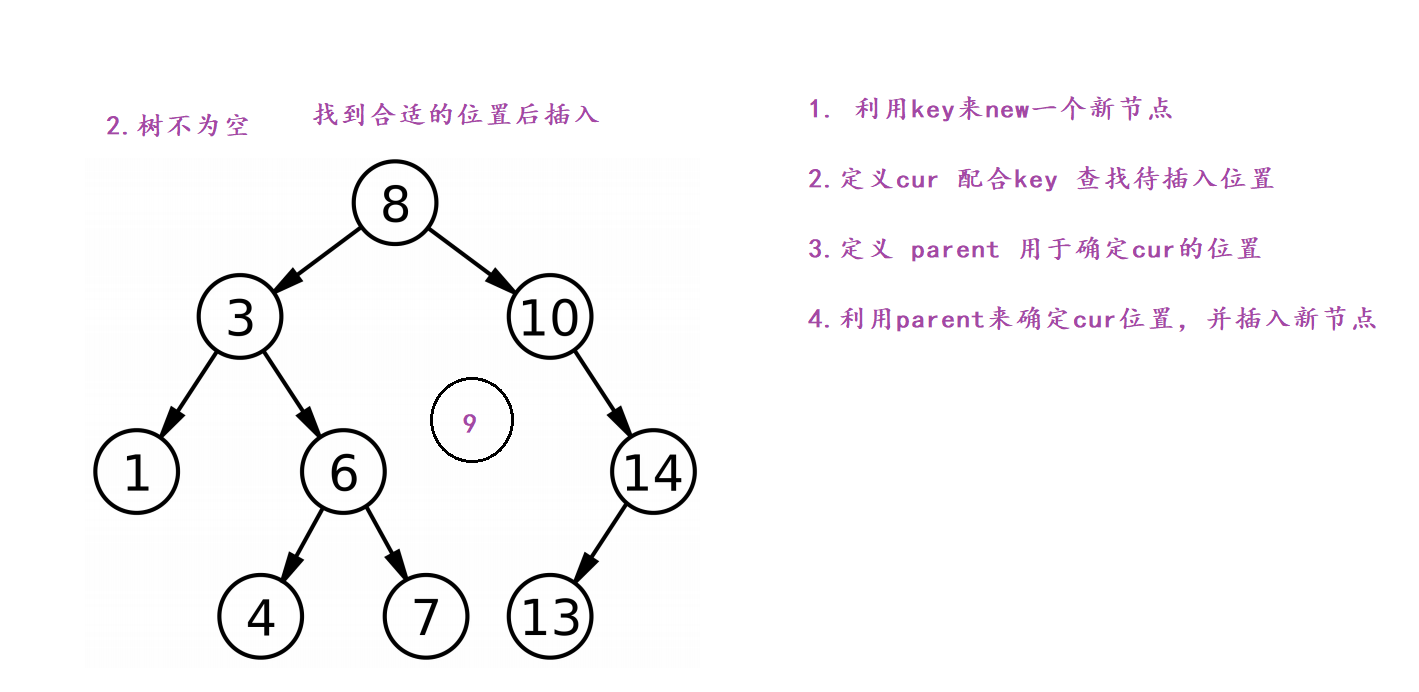
二叉树的插入

二叉树的插入有两种情况需要考虑，树为空时直接插入到root节点即可，树不为空则需按照左子树<根节点<右子树的规则找到待插入位置，并最终插入新节点。

cpp 复制代码

bool Insert(const K& key)
{
	//第一种情况--直接插入
	if (_root == nullptr)
	{
		_root = new Node(key);
		return true;
	}
	//非递归插入
	//1.寻找待插入的位置
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		parent = cur;
		if (key > cur->_key)
		{
			cur = cur->_right;
		}
		else if (key < cur->_key)
		{
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}
		//2.创建一个新节点
		Node* newNode = new Node(key);

		//利用 parent 找到 cur 的位置并在其插入新节点
		if (key > parent->_key)
		{
			parent->_right = newNode;
		}
		else
		{
			parent->_left = newNode;
		}
		return true;
}

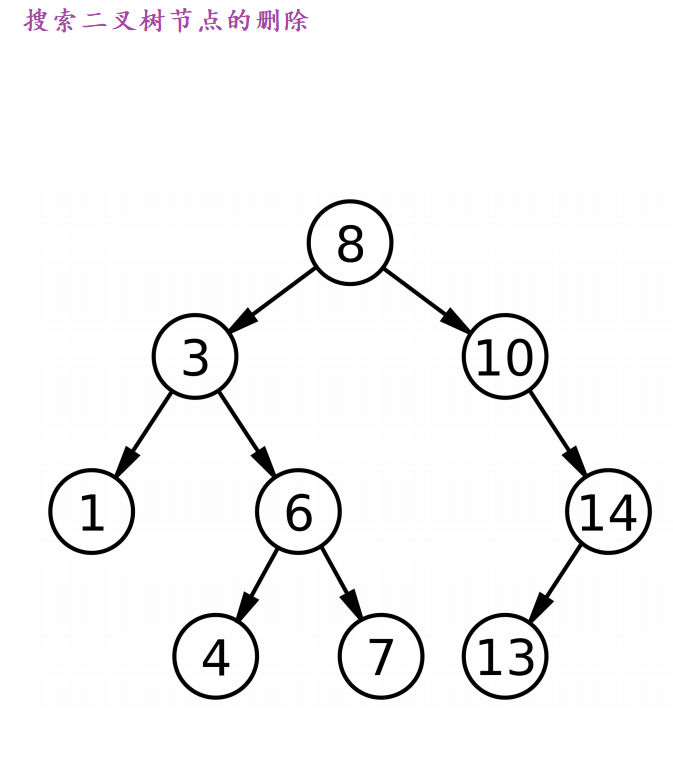
二叉搜索树的删除

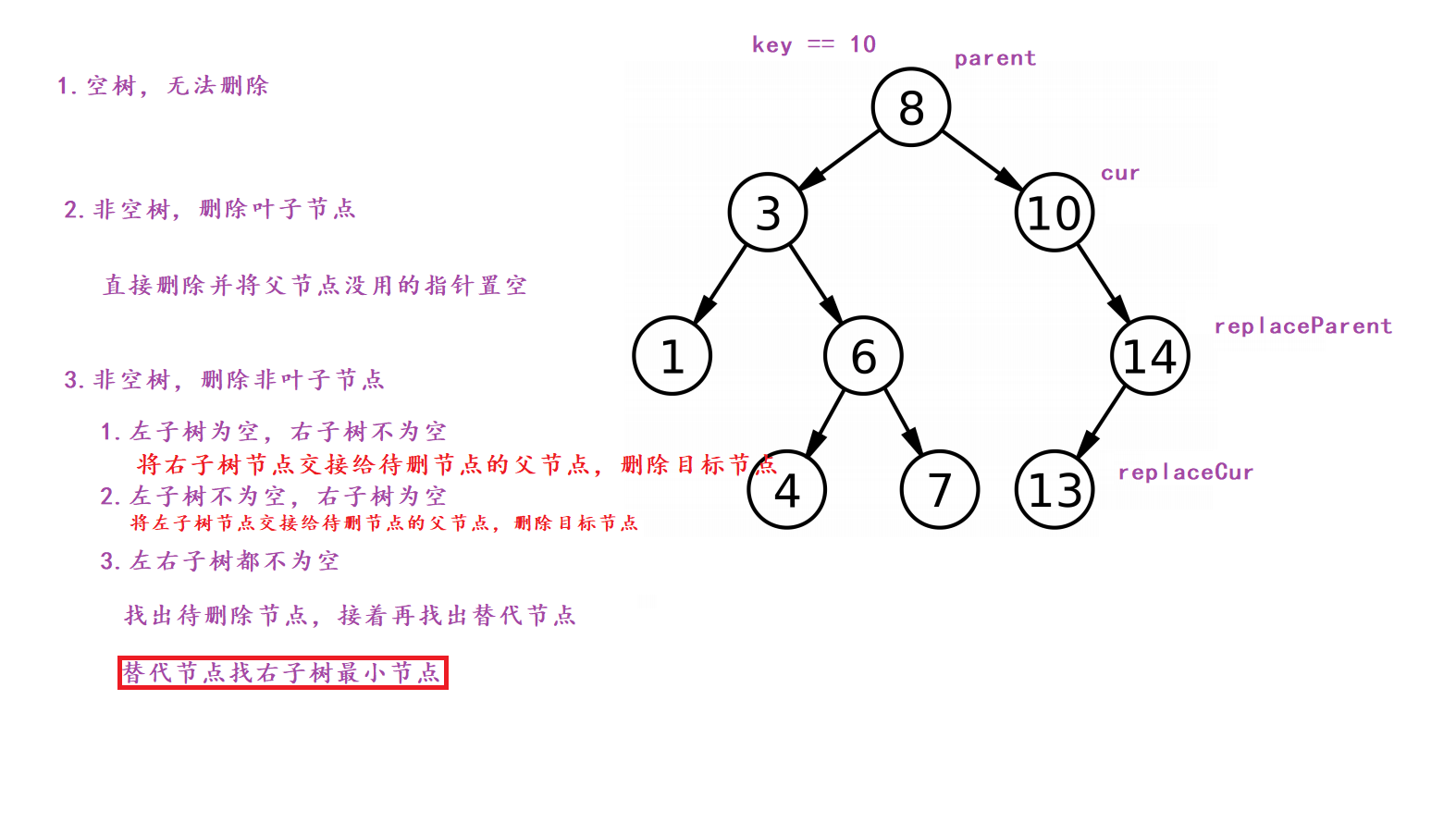
二叉搜索树的删除分五种情况，如图所示，但实际实现时可将第二种情况合并到3.1和3.2中一起解决。

cpp 复制代码

	//传入待删除的值
	bool Erase(const K& key)
	{
		Node* parent = _root;
		Node* cur = parent;

		while (cur)
		{
			//找到待删节点
			if (key > cur->_key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if(key < cur->_key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//key == cur->_key
				//删除目标节点
				if ( cur->_left == nullptr )
				{
					//1.左子树为空，交接右子树
					if (cur == _root)
					{
						//解决BST树只有一个节点的情况
						_root = cur->_right;
					}
					else
					{
						if (parent->_left == cur)
						{
							//解决BST树只有一个节点的情况
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}
					delete cur;
				}
				else if (cur->_right == nullptr)
				{
					//2.右子树为空，交接左子树
					if (cur == _root)
					{
						//解决BST树只有一个节点的情况
						_root = cur->_left;
					}
					else
					{
						if (parent->_left == cur)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
					}
					delete cur;
				}
				else
				{
					//3.左右均不为空
					Node* replaceParent = cur;
					Node* replaceCur = cur->_right;
					while (replaceCur->_left)
					{
						replaceParent = replaceCur;
						replaceCur = replaceCur->_left;
					}
					cur->_key = replaceCur->_key;
					
					if (replaceCur == replaceParent->_left)
					{
						replaceParent->_left = replaceCur->_right;
					}
					else
					{
						replaceParent->_right = replaceCur->_right;
					}
					delete replaceCur;
				}
				return true;
			}
		}
		return false;
	}