
🔥个人主页:艾莉丝努力练剑
❄专栏传送门:《C语言》、《数据结构与算法》、C语言刷题12天IO强训、LeetCode代码强化刷题
🍉学习方向:C/C++方向
⭐️人生格言:为天地立心,为生民立命,为往圣继绝学,为万世开太平

**前言:**牛客网和LeetCode的刷题都不可或缺,我们都要做一做,无论是参加竞赛还是笔试面试,至少能提升你的代码能力!洛谷的题目也可以去做一做。力扣的题目对提升代码能力很有帮助,需要有一点基础,几乎都是接口型的题目,关于接口型和IO型的区别我们在本专栏的第一篇【LeetCode】力扣题------轮转数组、消失的数字、数组串联中就介绍过了,这里不再赘述,我们进入今天的力扣题目介绍------
目录
正文
一、有效的括号
链接:20. 有效的括号
博主题解链接:借助数据结构------栈------解决经典例题【有效的括号】
推荐大家可以直接去看博主在力扣上面写的题解,博主介绍的还是比较详细的,博主写题解,尤其是数据结构算法题的题解,都是画图加说明,简单易懂。
题目描述:
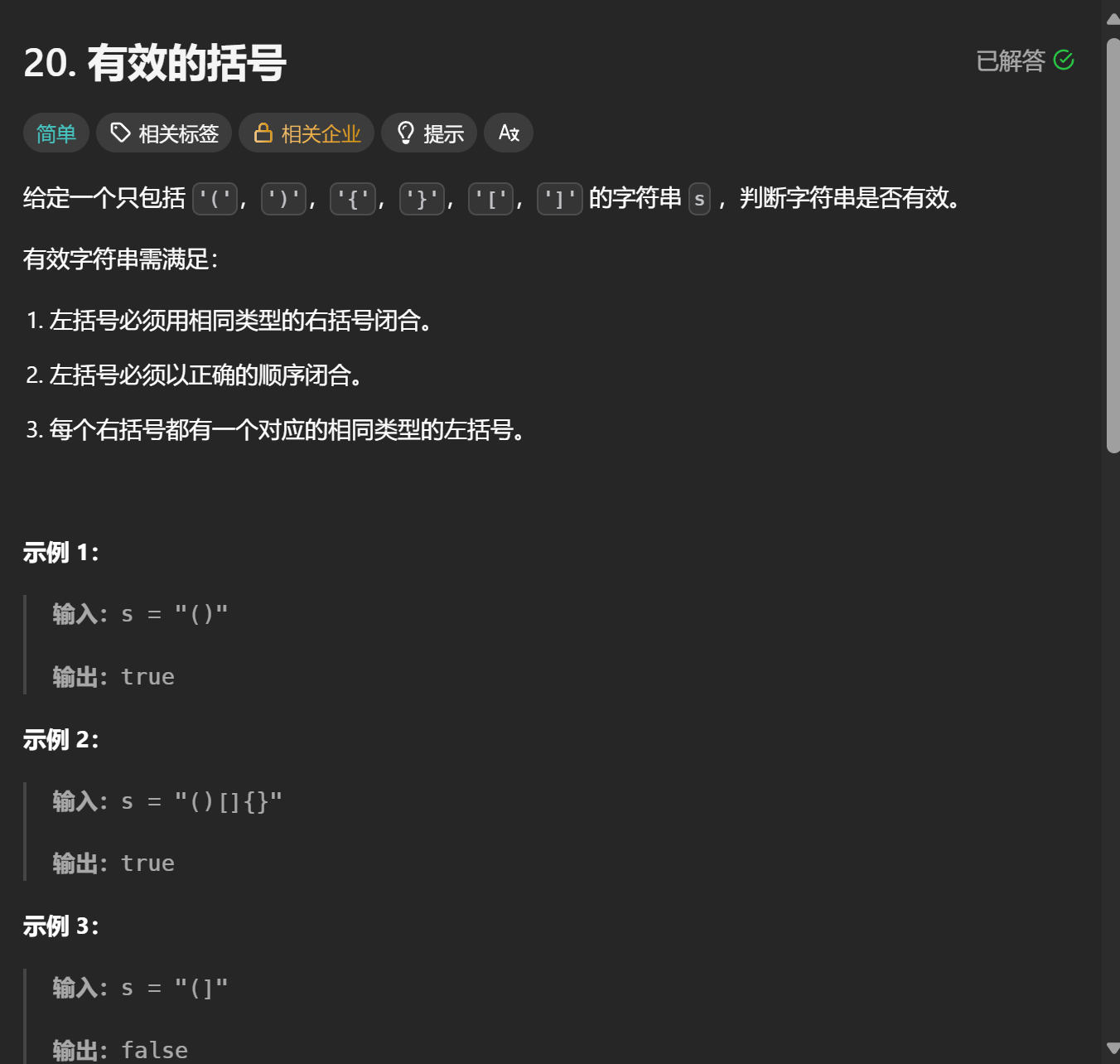
除了示例,本题也给了这样一个提示------

1、思路
我们的思路是:
借助数据结构------栈,遍历字符串,左括号入栈,是右括号就取栈顶元素比较,看是否匹配。
我们先来看看题目描述------
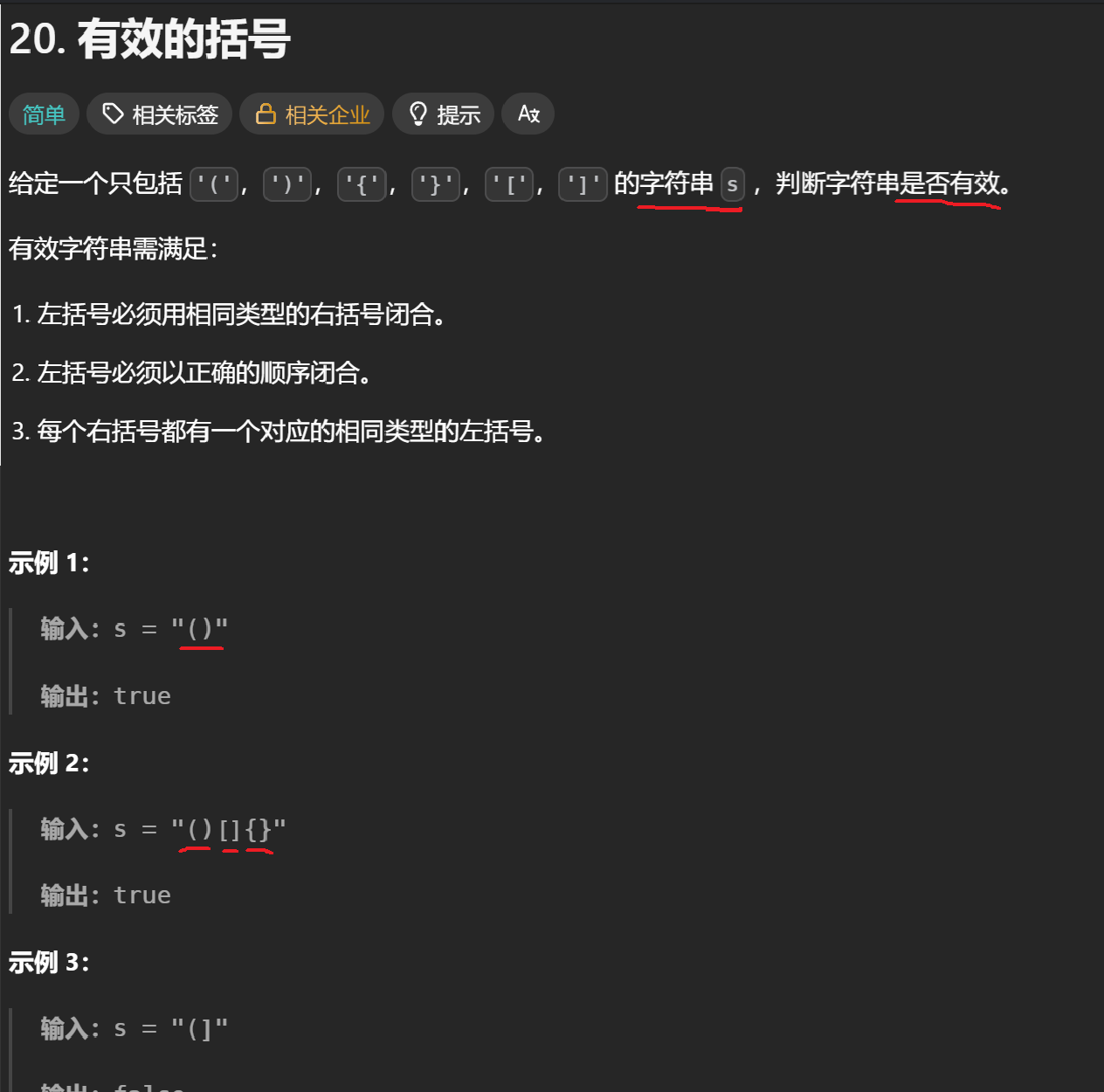
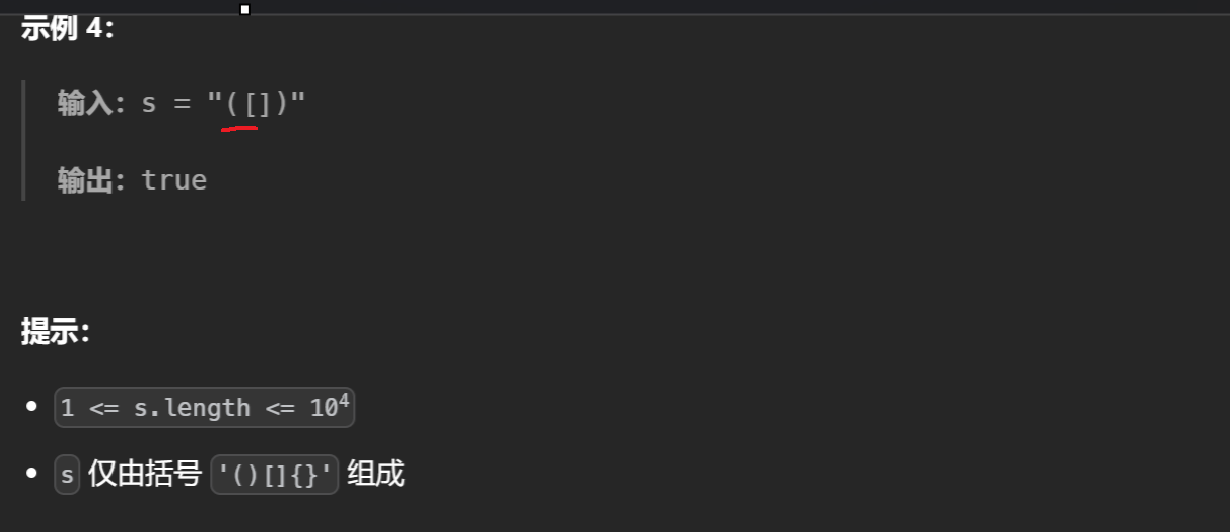
分析一下题目的意思------
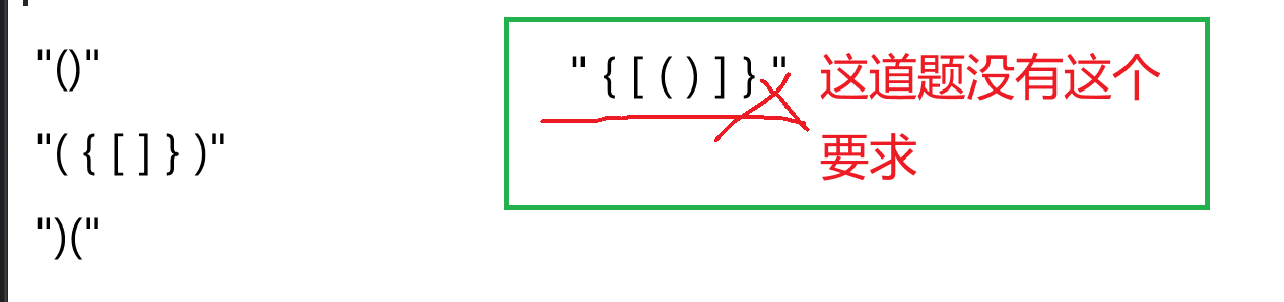

2、解题过程
像这种题目拿到手我们首先就是想到要画图,一定要有这个意识,数据结构的算法题一定要画图。
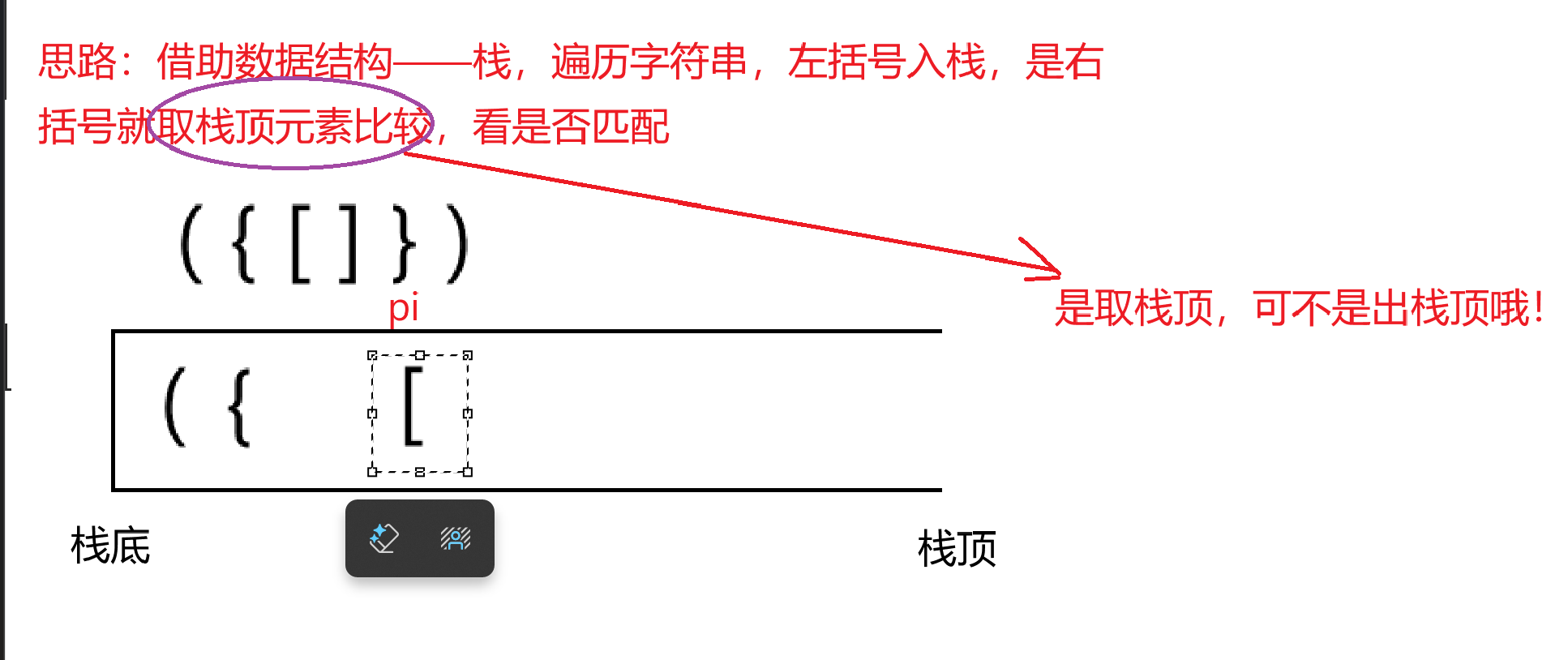
注意是取栈顶,可不是出栈顶哦!
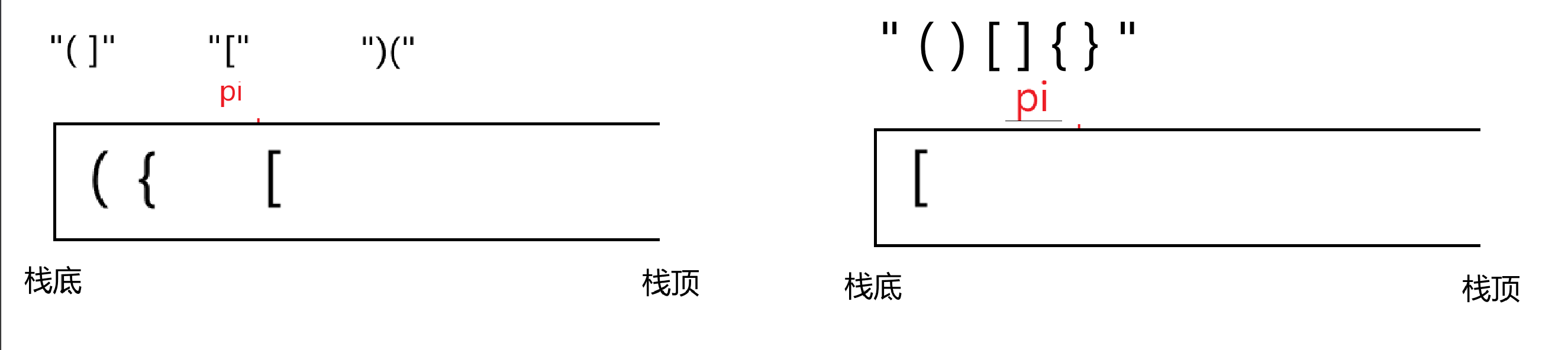
接下来我们就可以写代码了------
代码演示:
cpp
//定义栈的结构
typedef char STDataType;
typedef struct Stack
{
STDataType* arr;
int top;//定义栈中有效的数据个数
int capacity;//栈的空间大小
}ST;
//初始化
void STInit(ST* ps)
{
ps->arr = NULL;
ps->top = ps->capacity = 0;
}
//销毁
void STDestory(ST* ps)
{
if (ps->arr)
free(ps->arr);
ps->arr = NULL;
ps->top = ps->capacity = 0;
}
//入栈------栈顶
void STPush(ST* ps, STDataType x)
{
assert(ps);
//判断空间是否足够
if (ps->top == ps->capacity)
{
//增容
int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));
if (tmp == NULL)
{
perror("realloc fail!");
exit(1);
}
ps->arr = tmp;
ps->capacity = newCapacity;
}
//空间足够
ps->arr[ps->top++] = x;
}
//栈是否为空
bool STEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
//出栈------栈顶
void STPop(ST* ps)
{
assert(!STEmpty(ps));
ps->top--;
}
//取栈顶元素
STDataType STTop(ST* ps)
{
assert(!STEmpty(ps));
return ps->arr[ps->top - 1];
}
//获取栈中有效元素个数
int STSize(ST* ps)
{
assert(ps);
return ps->top;
}
//-----------------------以上是栈结构定义和常见方法-------------------------
bool isValid(char* s)
{
//借助数据结构------栈
ST st;
STInit(&st);
char* pi = s;
while(*pi != '\0')
{
//左括号入栈
if(*pi == '(' || *pi == '[' || *pi == '{')
{
STPush(&st,*pi);
}
else
{
//右括号------取栈顶,比较,匹配则出栈,不匹配直接返回false
//栈不为空才能取栈项
if(STEmpty(&st))
{
STDestory(&st);
return false;
}
char top = STTop(&st);
if((top == '(' && *pi != ')')
||(top == '[' && *pi != ']')
||(top == '{' && *pi != '}'))
{
STDestory(&st);
return false;
}
//本次是匹配的------出栈
STPop(&st);
}
pi++;
}
//判断栈是否为空,为空有效,非空无效
if(STEmpty(&st))
{
STDestory(&st);
return true;
}
STDestory(&st);
return false;
STDestory(&st);
return ret;
}复杂度:时间复杂度:O(N),空间复杂度:O(1)。
3、改进方案
最后我们【判断栈是否为空,为空有效,非空无效】那里代码太长了,我们用一个三目表达式就可以把它替换下来,这就是改进方案。
代码演示:
cpp
//定义栈的结构
typedef char STDataType;
typedef struct Stack
{
STDataType* arr;
int top;//定义栈中有效的数据个数
int capacity;//栈的空间大小
}ST;
//初始化
void STInit(ST* ps)
{
ps->arr = NULL;
ps->top = ps->capacity = 0;
}
//销毁
void STDestory(ST* ps)
{
if (ps->arr)
free(ps->arr);
ps->arr = NULL;
ps->top = ps->capacity = 0;
}
//入栈------栈顶
void STPush(ST* ps, STDataType x)
{
assert(ps);
//判断空间是否足够
if (ps->top == ps->capacity)
{
//增容
int newCapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));
if (tmp == NULL)
{
perror("realloc fail!");
exit(1);
}
ps->arr = tmp;
ps->capacity = newCapacity;
}
//空间足够
ps->arr[ps->top++] = x;
}
//栈是否为空
bool STEmpty(ST* ps)
{
assert(ps);
return ps->top == 0;
}
//出栈------栈顶
void STPop(ST* ps)
{
assert(!STEmpty(ps));
ps->top--;
}
//取栈顶元素
STDataType STTop(ST* ps)
{
assert(!STEmpty(ps));
return ps->arr[ps->top - 1];
}
//获取栈中有效元素个数
int STSize(ST* ps)
{
assert(ps);
return ps->top;
}
//-----------------------以上是栈结构定义和常见方法-------------------------
bool isValid(char* s)
{
//借助数据结构------栈
ST st;
STInit(&st);
char* pi = s;
while(*pi != '\0')
{
//左括号入栈
if(*pi == '(' || *pi == '[' || *pi == '{')
{
STPush(&st,*pi);
}
else
{
//右括号------取栈顶,比较,匹配则出栈,不匹配直接返回false
//栈不为空才能取栈项
if(STEmpty(&st))
{
STDestory(&st);
return false;
}
char top = STTop(&st);
if((top == '(' && *pi != ')')
||(top == '[' && *pi != ']')
||(top == '{' && *pi != '}'))
{
STDestory(&st);
return false;
}
//本次是匹配的------出栈
STPop(&st);
}
pi++;
}
//判断栈是否为空,为空有效,非空无效
// if(STEmpty(&st))
// {
// STDestory(&st);
// return true;
// }
// STDestory(&st);
// return false;
//写成三目表达式
bool ret = STEmpty(&st) ? true : false;
STDestory(&st);
return ret;
}复杂度:时间复杂度:O(N),空间复杂度:O(1)。
代码只有一个循环遍历,其它的都是条件判断,时间复杂度O(N),也没有额外申请空间,故空间复杂度O(1),复杂度较优。
4、其他思路------有局限性的一种思路

结尾
往期回顾:
【LeetCode&数据结构】单链表的应用------随机链表的复制问题、相交链表问题详解
【牛客&LeetCode&数据结构】单链表的应用------移除链表元素问题、链表分割问题详解
【牛客&LeetCode&数据结构】单链表的应用------合并两个有序链表问题、链表的回文结构问题详解
【LeetCode&数据结构】单链表的应用------反转链表问题、链表的中间节点问题详解
【LeetCode】力扣题------轮转数组、消失的数字、数组串联
【LeetCode】力扣题------轮转数组、消失的数字、数组串联
**结语:**本篇文章到这里就结束了,本文讲述的两道代码题并不适合C语言初学者,需要有一定的C语言基础,最好要学过数据结构与算法的算法复杂度和链表的知识,才能写出复杂度较优的代码来。大家一定要自己动手敲一敲,不敲的话不仅容易忘记,也不方便将来复习。