【金融机器学习】第三章：收益预测——Bryan Kelly, 修大成（中文翻译）

【金融机器学习】第三章：收益预测------Bryan Kelly, 修大成（中文翻译）

• 第三章：收益预测
• • [3.1 数据](#3.1 数据)
  • [3.2 实验设计](#3.2 实验设计)
  • • [3.2.1 示例：固定设计](#3.2.1 示例：固定设计)
    • [3.2.2 示例：递归设计](#3.2.2 示例：递归设计)
  • [3.3 基准：简单线性模型](#3.3 基准：简单线性模型)
  • [3.4 惩罚线性模型](#3.4 惩罚线性模型)
  • [3.5 降维](#3.5 降维)
  • • [3.5.1 主成分与偏最小二乘](#3.5.1 主成分与偏最小二乘)
    • [3.5.2 缩放PCA与监督PCA](#3.5.2 缩放PCA与监督PCA)
    • [3.5.3 从时间序列到面板预测](#3.5.3 从时间序列到面板预测)
    • [3.5.4 主组合](#3.5.4 主组合)
  • [3.6 决策树](#3.6 决策树)
  • [3.7 普通神经网络](#3.7 普通神经网络)
  • [3.8 比较分析](#3.8 比较分析)
  • [3.9 更复杂的神经网络](#3.9 更复杂的神经网络)
  • [3.10 "另类"数据的收益预测模型](#3.10 "另类"数据的收益预测模型)
  • • [3.10.1 文本分析](#3.10.1 文本分析)
    • [3.10.2 图像分析](#3.10.2 图像分析)

第三章：收益预测

实证资产定价的核心在于衡量资产风险溢价。这种衡量呈现两种形式：一种旨在描述和理解不同资产间风险溢价的差异，另一种聚焦于风险溢价的时间序列动态。作为收益的一阶矩，它自然成为审视金融机器学习实证文献的起点。一阶矩同时概括了两个方面：i) 投资者认为持有风险资产应获得的合理折现补偿（可能因市场摩擦导致的定价扭曲而存在偏差）；ii) 潜在投资者所面临投资机会的首要特征。

收益预测本质上是对资产条件预期超额收益的度量：¹

R i , t + 1 = E t [ R i , t + 1 ] + ϵ i , t + 1 , (3.1) R_{i,t+1} = \mathrm{E}t[R{i,t+1}] + \epsilon_{i,t+1}, \tag{3.1} Ri,t+1=Et[Ri,t+1]+ϵi,t+1,(3.1)

与式（1.2）相关， E t [ R i , t + 1 ] = E [ R i , t + 1 ∣ I t ] \mathrm{E}t[R{i,t+1}] = \mathrm{E}[R_{i,t+1}|\mathcal{I}_t] Et[Ri,t+1]=E[Ri,t+1∣It]表示基于信息集 I t \mathcal{I}t It的条件预测， ϵ i , t + 1 \epsilon{i,t+1} ϵi,t+1则捕捉了收益中所有剩余不可预测的变异。在构建市场数据的统计模型时，有必要认识到数据生成过程的极端复杂性：大量偏好各异、信息集迥异的投资者通过证券交易最大化自身福利，间歇性地形成价格序列，价格变动（以及股息、债券利息等现金流）最终产生收益序列。式（3.1）中条件期望所隐含的信息集，反映了所有影响t时刻定价的信息------无论是公开或私有、显性或隐性、明确或模糊。我们强调这一条件期望的复杂成因，是因为接下来将定义一个具体函数来描述其行为：

E t [ R i , t + 1 ] = g ⋆ ( z i , t ) . (3.2) \mathrm{E}t[R{i,t+1}] = g^{\star}(z_{i,t}). \tag{3.2} Et[Ri,t+1]=g⋆(zi,t).(3.2)

我们的目标是将 E t [ R i , t + 1 ] \mathrm{E}t[R{i,t+1}] Et[Ri,t+1]表示为研究者可获取的P维预测变量 z i , t z_{i,t} zi,t的普适函数 g ⋆ g^{\star} g⋆。即，我们希望找到一个不依赖于资产i或时间t的函数，一旦以 z i , t z_{i,t} zi,t为条件，便能完全解释所有资产和所有时期预期收益的异质性。² 通过保持函数形式的时空一致性，估计可以利用整个面板数据的信息，从而增强对单个资产预期收益估计的稳定性。这与某些传统资产定价方法形成对比------后者或需每期重新估计横截面模型，或需为每项资产独立估计时间序列模型（见Giglio等）。考虑到生成收益数据的复杂交易过程，这一"普适性"假设显得雄心勃勃：首先，研究者难以与市场参与者基于相同信息集进行条件预测（经典的Hansen-Richard批判）；其次，考虑到市场技术环境与文化背景的持续演进，以及可能影响价格的人类心理波动，普适函数 g ⋆ ( ⋅ ) g^{\star}(\cdot) g⋆(⋅)的概念似乎遥不可及。因此，尽管某些经济学家可能认为该框架过于灵活（允许任意函数形式和预测变量集），但实际上式（3.2）对预期收益模型施加了严苛限制。对于那些认为其限制过强的人而言，该框架若能稳健描述资产收益的各种行为（跨资产、跨时间、尤其是样本外表现），则可视为不可思议的成功。

¹ R i , t + 1 R_{i,t+1} Ri,t+1表示资产超额无风险收益率，资产索引 i = 1 , ... , N t i=1,\dots,N_t i=1,...,Nt，时间索引 t = 1 , ... , T t=1,\dots,T t=1,...,T。

² g ⋆ ( ⋅ ) g^{\star}(\cdot) g⋆(⋅)仅通过 z i , t z_{i,t} zi,t依赖于 z z z。在多数分析中，预测不会使用t期前的历史信息或其他股票信息，尽管后续引用的某些分析会推广此设定。

式（3.1）与（3.2）为机器学习收益预测文献提供了组织框架。本节按各论文采用的函数形式 g ( z i , t ) g(z_{i,t}) g(zi,t)分类，这些形式用于近似我们模板中的真实预测函数 g ⋆ ( z i , t ) g^{\star}(z_{i,t}) g⋆(zi,t)。我们着重阐述每篇论文的主要实证发现，突出其方法论创新与独特的实证结果。不同论文在预测变量选择上的具体差异虽不赘述，但读者应意识到这些差异同样是导致实证结果变异的重要原因（超越函数形式差异的影响）。

与前述时间序列和横截面研究议程相对应，存在两条独立的研究脉络。针对聚合资产（如股票或债券指数组合）的时间序列机器学习模型文献发展较早但规模较小。时间序列收益预测研究在Shiller（1981）提出超额波动率之谜后兴起于1980年代。随着研究者试图量化市场的超额波动程度，通过预测回归捕捉时变折现率成为计量经济学热点。时间序列预测文献更早发展，既因聚合组合收益数据的更早可得性，也因单一时间序列预测的相对简易性。但市场收益数据集的样本量较小，也限制了机器学习在该领域的应用------仅数百个月的收益观测值使得所谓"样本外"推断的真实性在数次研究尝试后便难以为继。

针对多资产面板收益预测的机器学习方法文献较新、规模更大且持续增长。它隶属于"收益横截面"研究范畴，因早期个股研究试图解释股票间无条件平均收益的差异------即数据简化为平均收益的单一横截面。但在现代形态中，所谓"横截面"研究已演变为真正的面板预测问题，目标在于同时解释条件预期收益的时序变异与横截面差异。该文献快速持续扩张的关键原因在于数据丰富性：面板的横截面维度可将时间序列观测值扩大数千倍（如个股、债券或期权案例）。尽管这些观测值存在明显的横截面相关性，但大部分个股收益变异是特异性的。此外，收益模式表现出高度异质性。换言之，面板特性为实证研究提供了大量待探索、记录并从经济框架理解的现象。

本节采用按机器学习方法分类的组织架构，每小节同时讨论时间序列与面板应用。鉴于横截面研究的主导地位，这部分将占据我们主要篇幅。

3.1 数据

多数金融机器学习文献研究一个经典数据集：美国股票的月度收益及主要来自CRSP-Compustat数据构建的股票层面信号。直至近期，构建该股票-月度面板仍缺乏标准化选择。不同研究者使用不同股票预测变量集（如Lewellen（2015）使用15个信号，Freyberger等（2020）使用36个，Gu等（2020b）使用94个），并施加不同观测筛选条件（如排除名义股价低于5美元的股票、剔除金融或公用事业等行业）。即便同名信号也常存在不同构建方式（如"价值"、"质量"等指标的各种变体）。

幸运的是，近期研究通过公开发布标准化股票面板数据及代码推动了数据决策的规范化，这些资源可直接从沃顿研究数据服务（WRDS）服务器获取。Jensen等（2021）构建了153个股票信号，提供源代码和文档以便用户检查、分析和修改实证选择。其数据不仅覆盖美国股票，还涵盖全球93个国家股票，并定期更新以反映CRSP-Compustat年度数据发布。这些资源可通过jkpfactors.com获取。Jensen等（2021）强调信号构建的标准化方法，力求在不同信号中统一使用CRSP-Compustat数据项。Chen和Zimmermann（2021）也在openassetpricing.com发布了美国股票代码与数据。

就聚合市场收益预测的标准化数据而言，Welch和Goyal（2008）发布了美国股市月度与季度收益及预测变量的更新数据。³ Rapach和Zhou（2022）提供了最新市场预测变量综述。

³ 数据见sites.google.com/view/agoyal145。

3.2 实验设计

模型估计与选择是机器学习定义的核心环节。自然，根据样本内（或训练样本）拟合选择最佳模型会夸大模型表现，因为增加模型参数化会机械提升样本内拟合。足够大的模型将完全拟合训练数据。一旦模型选择成为研究过程的一部分，我们便不能再依赖样本内表现评估模型。

常见的模型选择方法基于信息准则或交叉验证。Akaike（AIC）或Bayes/Schwarz（BIC）等信息准则允许研究者基于训练样本表现选择模型，通过引入与模型参数数量相关的概率理论惩罚项，抵消因参数增加导致的机械拟合改进。信息准则旨在从候选模型集中选出可能具有最佳样本外预测表现的模型。

交叉验证与AIC和BIC目标相同，但采用更数据驱动的方式。它基于"伪"样本外表现比较模型。交叉验证将观测分为训练集和验证集（伪样本外观测），通过隔离训练集与评估集，避免更大模型的机械优势，从而模拟样本外模型表现。交叉验证根据模型在伪样本外数据中的预测表现进行选择。

信息准则与交叉验证各有优劣。某些情况下，AIC与交叉验证会渐近等价地选择模型（Stone，1977；Nishii，1984）。信息准则的劣势在于其推导依赖特定理论假设，若数据或模型违背这些假设，则需修正理论准则且修正可能困难或不可行。交叉验证实施通常更易适应具有挑战性的数据特性（如序列依赖或极端值），且可应用于几乎所有机器学习算法（Arlot和Celisse，2010）。但因其随机重复性质，交叉验证可能产生噪声更大的模型评估且计算成本较高。随着高性能计算成本下降，机器学习文献已逐渐转向主要依赖交叉验证，因其明显的适应性与普适性。

为具体说明交叉验证的模型选择及其在机器学习实证设计中的定位，我们概述Gu等（2020b）及后续多项研究采用的示例设计。

3.2.1 示例：固定设计

设完整研究样本包含时间序列观测 t = 1 , . . . , T t = 1, ..., T t=1,...,T。首先展示固定样本分割方案。将T个观测分为三个互斥子样本：首个子样本为"训练"样本，用于估计所有候选模型，包含 t = 1 , . . . , T train t = 1, ..., T_{\text{train}} t=1,...,Ttrain的 T train T_{\text{train}} Ttrain个观测。候选模型集通常由一组"超参数"（亦称"调参参数"）决定。定义连续候选模型集的超参数示例是岭回归中的收缩参数，而描述离散模型集的调参参数示例是PCA选取的主成分数量。

第二个"验证"样本包含伪样本外观测。验证样本的预测基于训练样本估计的模型构建。验证样本上的模型表现（通常定义为模型估计器的目标函数）决定具体选择的超参数值（即具体模型）。验证样本包含 t = T train + 1 , . . . , T train + T validate t = T_{\text{train}} + 1, ..., T_{\text{train}} + T_{\text{validate}} t=Ttrain+1,...,Ttrain+Tvalidate的 T validate T_{\text{validate}} Tvalidate个观测。需注意，虽然原始模型仅基于前 T train T_{\text{train}} Ttrain个数据点估计，但一旦选定模型设定，其参数通常会基于完整 T train + T validate T_{\text{train}} + T_{\text{validate}} Ttrain+Tvalidate样本重新估计，以在构建样本外预测时充分利用样本内数据效率。

验证样本拟合当然非真正样本外，因其用于调参，故验证表现本身受选择偏差影响。因此需使用第三个"测试"样本（既不用于估计也不用于调参）进行预测表现的最终评估。测试样本包含 t = T train + T validate + 1 , . . . , T train + T validate + T test t = T_{\text{train}} + T_{\text{validate}} + 1, ..., T_{\text{train}} + T_{\text{validate}} + T_{\text{test}} t=Ttrain+Tvalidate+1,...,Ttrain+Tvalidate+Ttest的 T test T_{\text{test}} Ttest个观测。

此简化设计示例有两点值得强调：首先，本例最终模型基于 T train + T validate T_{\text{train}} + T_{\text{validate}} Ttrain+Tvalidate数据一次性估计完成。但若在测试期递归重新估计模型，研究者可产生更高效的样本外预测。依赖固定样本分割的原因可能是候选模型训练计算强度大，使得重新训练不可行或计算成本过高（见Jiang等（2022）的CNN分析）。

其次，本例样本分割遵循数据时间顺序。该设计动机是避免时间反向的信息无意泄露。进一步地，时间序列应用常在训练与验证样本间设置隔离样本，以防样本间序列相关性导致验证偏差。序列相关性越强，隔离期应越长。

训练与验证样本的时间排序非绝对必要，且可能低效使用模型选择数据。例如，本设计时间排序的一个变体是用更传统的K折交叉验证方案替代固定验证样本。此时前 T train + T validate T_{\text{train}} + T_{\text{validate}} Ttrain+Tvalidate个观测可生成K个不同验证样本，从而可能做出更知情的模型选择。这适用于序列不相关数据。图3.1展示了K折交叉验证方案，其通过K个验证样本的平均表现进行模型选择。

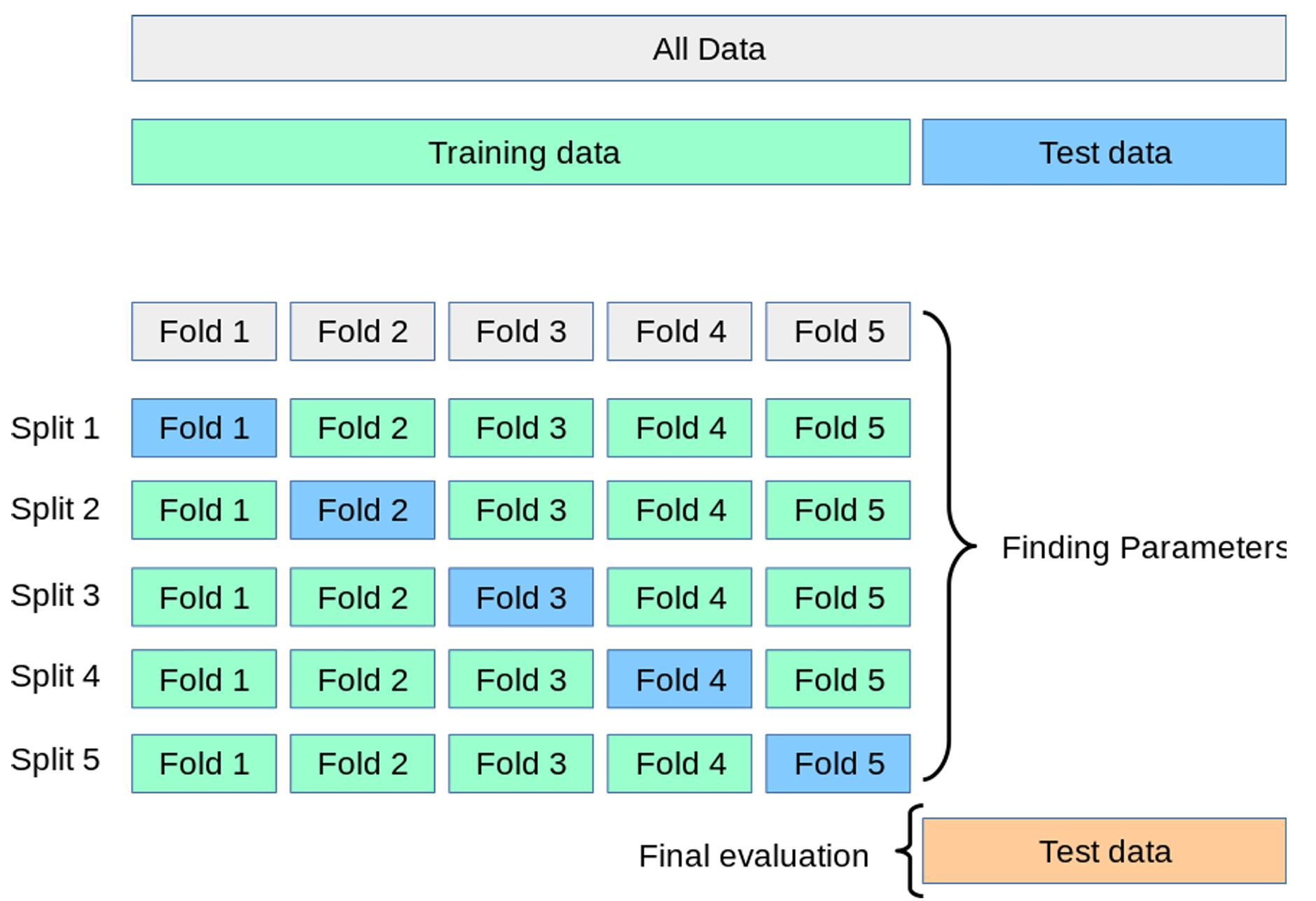
图3.1：标准K折交叉验证示意图

3.2.2 示例：递归设计

当构建时间t实现的收益样本外预测时，分析师通常希望使用最新样本估计模型。此时训练与验证样本基于 1 , . . . , t − 1 1,...,t-1 1,...,t−1的观测。例如对训练/验证样本五五分割，上述固定设计将调整为训练 1 , . . . , ⌊ t − 1 2 ⌋ 1,...,\lfloor\frac{t-1}{2}\rfloor 1,...,⌊2t−1⌋，验证 ⌊ t − 1 2 ⌋ + 1 , . . . , t − 1 \lfloor\frac{t-1}{2}\rfloor+1,...,t-1 ⌊2t−1⌋+1,...,t−1。随后基于截至 t − 1 t-1 t−1的全部数据重新估计选定模型，生成t时刻样本外预测。

在 t + 1 t+1 t+1时刻重复整个训练/验证/测试流程：训练使用 1 , . . . , ⌊ t 2 ⌋ 1,...,\lfloor\frac{t}{2}\rfloor 1,...,⌊2t⌋，验证使用 ⌊ t 2 ⌋ + 1 , . . . , t \lfloor\frac{t}{2}\rfloor+1,...,t ⌊2t⌋+1,...,t，重新估计选定模型至t时刻生成样本外预测。该递归迭代直至为观测T生成最终样本外预测。注意由于每期重新验证，选定模型可在递归过程中变化。图3.2展示此时序递归交叉验证方案。

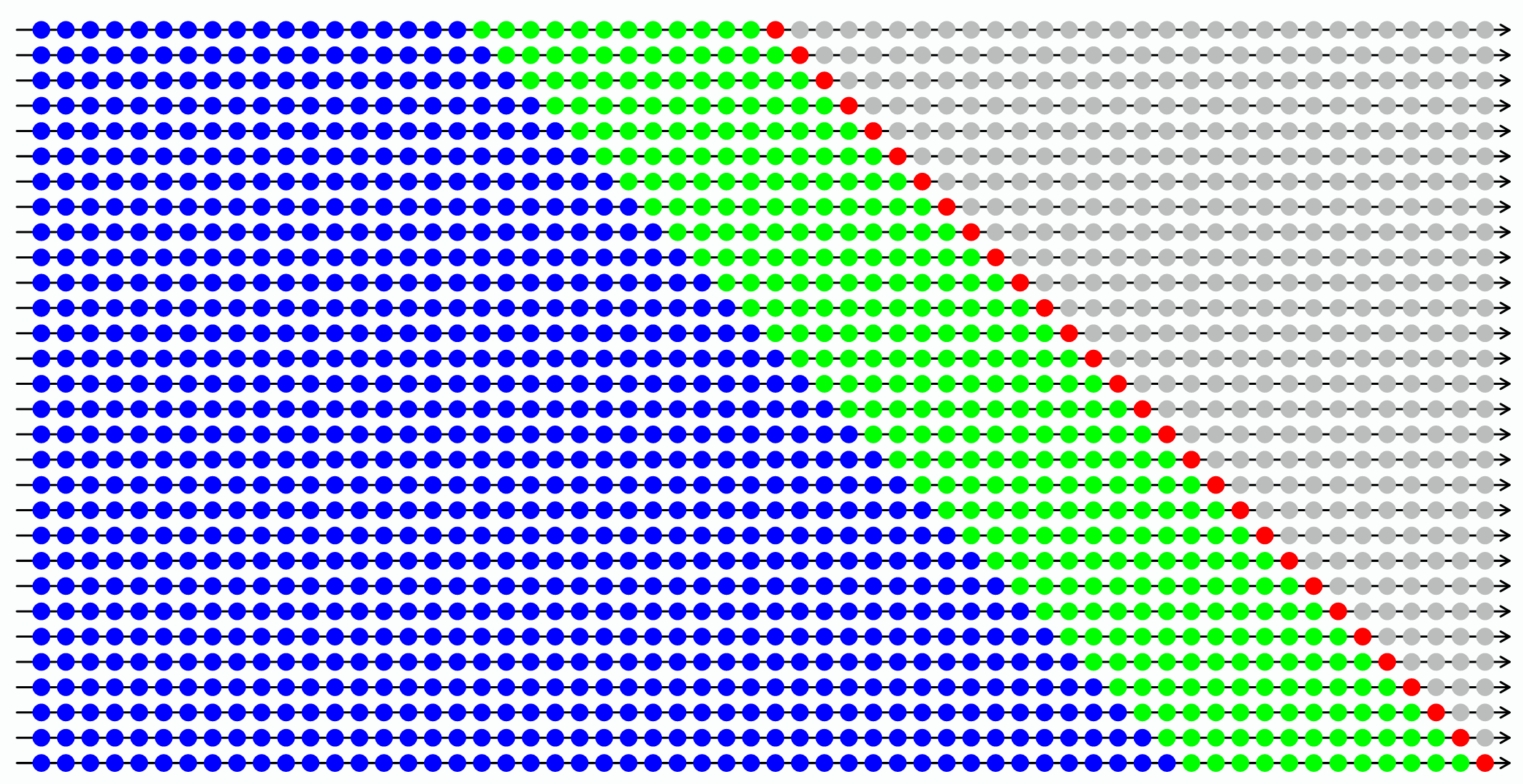
图3.2：递归时序交叉验证示意图

注：蓝点代表训练观测，绿点代表验证观测，红点代表测试观测。每行代表递归设计的一个步骤。本图对应训练窗口扩展（非滚动）情形。

该设计的常见变体是使用滚动而非扩展的训练窗口。若怀疑数据结构不稳定或出于其他建模/测试需求保持训练样本量恒定，滚动窗口更为有利。

3.3 基准：简单线性模型

股票收益预测的基础面板模型是简单线性模型，任何机器学习方法都应与之比较。给定股票预测特征集 z i , t z_{i,t} zi,t，线性面板模型固定预测函数为 g ( z i , t ) = β ′ z i , t g(z_{i,t}) = \beta' z_{i,t} g(zi,t)=β′zi,t：

R i , t + 1 = β ′ z i , t + ϵ i , t + 1 . (3.3) R_{i,t+1} = \beta' z_{i,t} + \epsilon_{i,t+1} \tag{3.3}. Ri,t+1=β′zi,t+ϵi,t+1.(3.3)

该模型存在多种估计量，适用于误差协方差矩阵的不同结构假设。实证金融研究中最流行的是Fama和MacBeth（1973）回归。Petersen（2008）分析了Fama-MacBeth的计量特性并与其他面板估计量比较。

Haugen和Baker（1996）与Lewellen（2015）是横截面收益机器学习文献的先驱。首先，他们采用较多信号：Haugen和Baker（1996）使用约40个连续变量和行业哑变量，Lewellen（2015）使用15个连续变量。其次，他们递归估计式（3.3）的面板线性模型，并强调训练模型的样本外表现。这区别于文献中常见的基于一两个特征分箱股票的实证流程------本质上是"零参数"收益预测模型，其断言 g ( z i , t ) g(z_{i,t}) g(zi,t)的函数形式而不进行估计。⁴ 两位作者均以交易策略表现的经济术语评估样本外模型表现。Haugen和Baker（1996）还分析了国际数据，Lewellen（2015）则额外分析了预测 R 2 R^{2} R2的准确性。

⁴ 据我们所知，Basu（1977）最早进行基于特征的组合排序，对股票市盈率进行五分位排序。Fama和French（1992）采用该方法后，组合排序成为分析股票收益预测因子有效性的主流方法。

Haugen和Baker（1996）表明，基于线性模型收益预测构建的优化组合跑赢市场，且在他们研究的五个国家均成立。其最有趣的发现之一是预测模式的稳定性，表3.1（基于其论文表1）重现了该结果。重要预测变量在前半样本的系数不仅符号相同，且幅度和t统计量在后半样本惊人相似。

因子	1979/01-1986/06 均值	1979/01-1986/06 t值	1986/07-1993/12 均值	1986/07-1993/12 t值
一个月超额收益	− 0.97 % -0.97\% −0.97%	-17.04	− 0.72 % -0.72\% −0.72%	-11.04
十二个月超额收益	0.52 % 0.52\% 0.52%	7.09	0.52 % 0.52\% 0.52%	7.09
交易量/市值	− 0.35 % -0.35\% −0.35%	-5.28	− 0.20 % -0.20\% −0.20%	-2.33
两个月超额收益	− 0.20 % -0.20\% −0.20%	-4.97	− 0.11 % -0.11\% −0.11%	-2.37
盈余价格比	0.27 % 0.27\% 0.27%	4.56	0.26 % 0.26\% 0.26%	4.42
净资产收益率	0.24 % 0.24\% 0.24%	4.34	0.13 % 0.13\% 0.13%	2.06
账面市值比	0.35 % 0.35\% 0.35%	3.90	0.39 % 0.39\% 0.39%	6.72
交易量趋势	− 0.10 % -0.10\% −0.10%	-3.17	− 0.09 % -0.09\% −0.09%	-2.58
六个月超额收益	0.24 % 0.24\% 0.24%	3.01	0.19 % 0.19\% 0.19%	2.55
现金流价格比	0.13 % 0.13\% 0.13%	2.64	0.26 % 0.26\% 0.26%	4.42
现金流价格比波动性	− 0.11 % -0.11\% −0.11%	-2.55	− 0.15 % -0.15\% −0.15%	-3.38

表3.1：Haugen和Baker（1996）的月均因子收益

Lewellen（2015）表明，在全美股票横截面中，面板线性模型的样本外 R 2 R^{2} R2约为每月1%且高度显著，证明其能定量对齐预测收益与实现收益的_水平_。这区别于排序方法------后者通常评估其区分高低预期收益股票的能力（即进行相对比较而不必匹配幅度）。此外，15变量线性模型转化为令人印象深刻的交易策略表现，如表3.2（重现自Lewellen（2015）表6A）所示。等权重多空策略（买入模型预测最高十分位、做空最低十分位）的样本外年化夏普比为1.72（市值加权十分位为0.82）。Haugen和Baker（1996）与Lewellen（2015）的证据共同表明，简单线性面板模型能实时估计多预测变量的有效组合用于收益预测和交易策略构建。

	等权重预测	等权重平均	等权重标准差	等权重t值	等权重夏普比	市值加权预测	市值加权平均	市值加权标准差	市值加权t值	市值加权夏普比
面板A：全样本股票
低(L)	-0.90	-0.32	7.19	-0.84	-0.15	-0.76	0.11	6.01	0.37	0.06
2	-0.11	0.40	5.84	1.30	0.24	-0.10	0.45	4.77	1.89	0.32
3	0.21	0.60	5.46	2.06	0.38	0.21	0.65	4.65	2.84	0.49
4	0.44	0.78	5.28	2.74	0.51	0.44	0.69	4.67	2.97	0.51
5	0.64	0.81	5.36	2.82	0.52	0.63	0.81	5.01	3.34	0.56
6	0.83	1.04	5.36	3.62	0.67	0.82	0.88	5.22	3.28	0.58
7	1.02	1.12	5.55	3.68	0.70	1.01	1.04	5.67	3.46	0.64
8	1.25	1.31	5.97	4.04	0.76	1.24	1.15	6.03	3.62	0.66
9	1.55	1.66	6.76	4.38	0.85	1.54	1.34	6.68	3.80	0.69
高(H)	2.29	2.17	7.97	4.82	0.94	2.19	1.66	8.28	3.73	0.70
H-L	3.20	2.49	5.02	10.00	1.72	2.94	1.55	6.56	4.51	0.82

表3.2：Lewellen（2015）的月均因子收益与年化夏普比

转向时间序列分析，Shiller（1981）的超额波动率之谜催生了大量文献以量化折现率时变程度，以及解释折现率动态行为的理论工作（如Campbell和Cochrane，1999；Bansal和Yaron，2004；Gabaix，2012；Wachter，2013）。捕捉折现率变动的实证工具首选线性时间序列回归。如Rapach和Zhou（2013）股市预测综述指出，最流行的预测变量是聚合价格-股息比（如Campbell和Shiller，1988），尽管数十个其他预测变量也被研究。总体而言，文献聚焦于单变量或小型多元预测模型，偶尔辅以经济约束如市场收益预测的非负限制（Campbell和Thompson，2008）或现值恒等式的跨方程约束（Cochrane，2008；Van Binsbergen和Koijen，2010）。Welch和Goyal（2008）的著名批评指出，简单线性模型丰富的样本内股市预测证据难以推广至样本外。但Rapach等（2010）表明预测组合技术能产生可靠的样本外市场预测。

3.4 惩罚线性模型

借用进化生物学术语，Haugen和Baker（1996）与Lewellen（2015）的线性模型是金融文献中的"过渡物种"。与传统计量方法类似，研究者先验固定模型设定；但与机器学习相似，他们考虑了远超前人的大量预测变量并强调样本外预测表现。

尽管这些论文研究数十个收益预测变量，但文献分析的预测特征总数达数百个（Harvey等，2016；Hou等，2018；Jensen等，2021）。若进一步考虑预测关系的状态依赖性（如Schaller和Norden，1997；Cujean和Hasler，2017），线性模型的参数量会迅速膨胀至数千个。Gu等（2020b）考虑预测股票-月度收益面板的基线线性设定，使用约1,000个预测变量------包含约100个已证明对个股收益有预测力的股票特征与10个对市场收益预测有效的宏观金融变量的乘积交互项。尽管这些预测变量在前期研究中单独显示潜力，Gu等（2020b）表明OLS无法同时稳定拟合如此多参数，导致灾难性样本外表现：预测 R 2 R^{2} R2为-35%/月，基于此预测的交易策略跑输市场。

OLS估计在众多预测变量下失效并不意外。当预测变量数P接近观测数NT时，线性模型变得低效甚至不一致，开始过度拟合噪声而非提取信号。这对信号噪声比 notoriously 低的收益预测问题尤为棘手。

第2节关于"复杂"模型的讨论得出核心结论：避免过拟合的关键是通过正则化约束模型。这可通过将复杂度（第2节定义的c）推至远高于1（隐式正则化最小二乘估计量）或通过岭回归等显式惩罚实现。简单线性模型两者皆未采用------其复杂度处于高方差区间（远高于0但未达1），且未使用显式正则化。

惩罚线性模型的预测函数与式（3.3）的简单线性模型相同，即仍仅考虑原始未转换预测变量。惩罚方法通过在原始损失函数上附加惩罚项（如流行的"弹性网络"惩罚）形成惩罚损失：

L ( β ; ρ , λ ) = ∑ i = 1 N ∑ t = 1 T ( R i , t + 1 − β ′ z i , t ) 2 + λ ( 1 − ρ ) ∑ j = 1 P ∣ β j ∣ + 1 2 λ ρ ∑ j = 1 P β j 2 . (3.4) \mathcal{L}(\beta;\rho,\lambda) = \sum_{i=1}^{N}\sum_{t=1}^{T}\left(R_{i,t+1}-\beta' z_{i,t}\right)^{2} + \lambda(1-\rho)\sum_{j=1}^{P}|\beta_{j}| + \frac{1}{2}\lambda\rho\sum_{j=1}^{P}\beta_{j}^{2}. \tag{3.4} L(β;ρ,λ)=i=1∑Nt=1∑T(Ri,t+1−β′zi,t)2+λ(1−ρ)j=1∑P∣βj∣+21λρj=1∑Pβj2.(3.4)

弹性网络包含两个非负超参数 λ \lambda λ和 ρ \rho ρ，涵盖两个著名正则化特例。 ρ = 1 \rho=1 ρ=1对应岭回归，采用 ℓ 2 \ell_{2} ℓ2参数惩罚使所有系数估计向零收缩但不产生精确零； ρ = 0 \rho=0 ρ=0对应lasso，采用绝对值" ℓ 1 \ell_{1} ℓ1"参数惩罚------若惩罚足够大，lasso的几何特性会使部分协变量系数精确为零，故lasso可视为变量选择与收缩双重工具。 ρ \rho ρ中间值时，弹性网络鼓励具有不同岭与lasso组合效应的简单模型。

Gu等（2020b）表明，引入弹性网络惩罚可逆转股票-月度收益预测面板中OLS估计的失败：样本外预测 R 2 R^{2} R2转为正，基于弹性网络预测的等权重多空十分位差策略年化夏普比达1.33。换言之，OLS表现不佳并非源于1,000个预测变量包含的预测信息薄弱，而是沉重参数负担导致的统计成本（过拟合与低效）。He等（2022a）分析弹性网络集成发现，最佳弹性网络模型随时间变化较快，而集成能有效捕捉这些变化。Rapach等（2013）将式（3.4）应用于跨国市场收益预测。

惩罚回归是金融领域最常用的机器学习工具之一，主要因其概念与计算易处理性。例如岭回归估计量有闭式解，故与OLS计算复杂度相同。lasso估计量通常无闭式解，需数值计算，但高效算法已内置于主流统计软件（包括Stata、Matlab及各类Python库）。

Freyberger等（2020）结合惩罚回归与广义加性模型（GAM）预测股票-月度收益面板。其应用中，函数 p k ( z i , t ) p_{k}(z_{i,t}) pk(zi,t)是对 z i , t z_{i,t} zi,t中P个变量的逐元素非线性变换：

g ( z i , t ) = ∑ k = 1 K β ~ k ′ p k ( z i , t ) . (3.5) g(z_{i,t}) = \sum_{k=1}^{K}\tilde{\beta}{k}' p{k}(z_{i,t}) \tag{3.5}. g(zi,t)=k=1∑Kβ~k′pk(zi,t).(3.5)

该模型通过使用 k = 1 , . . . , K k=1,...,K k=1,...,K个此类非线性变换扩展预测变量集，每个变换k有独立的 Q × 1 Q \times 1 Q×1线性回归系数向量 β ~ k \tilde{\beta}_{k} β~k。Freyberger等（2020）采用二次样条基函数，但基函数选择无限可能，且非线性变换可联合应用于多个预测变量（而非逐元素）。

由于非线性项以加性形式进入，GAM预测可采用与任何线性模型相同的估计工具。但支撑GAM的级数展开概念会快速倍增模型参数，故惩罚控制自由度通常有益于样本外表现。Freyberger等（2020）采用称为群lasso（Huang等，2010）的惩罚函数：

λ ∑ j = 1 Q ( ∑ k = 1 K β ~ k , j 2 ) 1 / 2 , (3.6) \lambda \sum_{j=1}^{Q} \left( \sum_{k=1}^{K} \tilde{\beta}_{k,j}^{2} \right)^{1/2}, \tag{3.6} λj=1∑Q(k=1∑Kβ~k,j2)1/2,(3.6)

其中 β ~ k , j \tilde{\beta}_{k,j} β~k,j是股票信号j的第k个基函数系数。该惩罚特别适合样条展开设定------如其名所示，群lasso会选择与给定特征j关联的所有K个样条项，或全部不选。

Freyberger等（2020）的群lasso结果显示，文献中常见股票信号仅不到半数具有独立收益预测力。他们还证实了非线性的重要性，表明完整非线性设定的样本外交易策略表现优于嵌套线性设定。

Chinco等（2019）同样使用lasso研究收益预测。其研究有多项独特之处：首先采用高频数据------在滚动30分钟回归中预测一分钟后的股票收益；其次为每只股票建立独立模型，使其分析成为大量时间序列线性回归的集合；第三，不使用标准股票特征作为预测变量，其特征集包含NYSE横截面所有股票的三期滞后一分钟收益。该模型最有趣之处在于其对跨股票预测效应的包容，最终回归设定为：

R i , t = α i + β i , 1 ′ R t − 1 + β i , 2 ′ R t − 2 + β i , 3 ′ R t − 3 + ϵ i , t , i = 1 , . . . , N (3.7) R_{i,t} = \alpha_{i} + \beta_{i,1}' R_{t-1} + \beta_{i,2}' R_{t-2} + \beta_{i,3}' R_{t-3} + \epsilon_{i,t}, \quad i = 1, ..., N \tag{3.7} Ri,t=αi+βi,1′Rt−1+βi,2′Rt−2+βi,3′Rt−3+ϵi,t,i=1,...,N(3.7)

其中 R t R_{t} Rt是t分钟所有股票收益的向量。作者对每只股票i用lasso估计该模型，通过10折交叉验证选择股票特定惩罚参数。他们发现主导预测变量在不同时期差异显著，且往往与报告基本面新闻的股票收益相关。这些模式的经济洞见尚未充分挖掘，但预测证据的强度表明，高频收益的机器学习方法有望揭示关于信息流及其引致的资产联合动态的新现象。

Avramov等（2022b）研究公司基本面动态如何关联后续股价漂移。他们对基本面动态细节持不可知论观点，数据驱动地考虑所有季度Compustat数据项相对最近三季均值的偏离，而非先验手动选择特定基本面。这些大量偏离通过监督学习聚合成单一收益预测指标。具体而言，他们用合并面板lasso回归预测股票i的收益，使用股票i的所有Compustat偏离，将回归拟合值称为基本面偏离指数（FDI）。多空最高与最低FDI股票的市值加权十分位差策略，相对Fama-French-Carhart四因子模型的年化样本外信息比为0.8。

3.5 降维

机器学习的正则化通常有益于高维预测问题，因其减少自由度。实现方式多样：惩罚线性模型通过向零收缩系数和/或将部分系数强制为零来减少自由度，但当预测变量高度相关时可能产生次优预测。设想每个预测变量等于预测目标加i.i.d.噪声项的情境，此时合理预测方案是在单变量预测回归中简单使用预测变量均值。

预测变量平均是降维的核心思想。形成预测变量的线性组合有助于降噪以更好提取信号。我们首先讨论两种经典降维技术------主成分回归（PCR）与偏最小二乘（PLS），随后介绍为低信噪比场景设计的PCA扩展------缩放PCA与监督PCA。这些方法作为市场收益或宏观经济变量时间序列预测的降维工具出现在文献中。接着我们扩展其使用至横截面收益预测的面板环境，最后介绍针对该问题的新近金融专用方法"主组合分析"。本节聚焦降维在预测中的应用------降维在资产定价中的作用远超预测范畴，我们将在后续章节探讨。例如多种基于PCA的方法是潜在因子分析的核心，第4节将其归类为机器学习因子定价模型。

3.5.1 主成分与偏最小二乘

我们在通用预测回归设定中形式化讨论这两种方法：

y t + h = x t ′ θ + ϵ t + h , (3.8) y_{t+h} = x_{t}' \theta + \epsilon_{t+h}, \tag{3.8} yt+h=xt′θ+ϵt+h,(3.8)

其中y可指市场收益或GDP增长、失业率、通胀等宏观经济变量， x t x_{t} xt是 P × 1 P \times 1 P×1预测变量向量，h为预测期限。

降维思想是用低维"因子" f t f_{t} ft替代高维预测变量， f t f_{t} ft概括 x t x_{t} xt的有用信息。其关系通常表述为标准因子模型：

x t = β f t + u t . (3.9) x_{t} = \beta f_{t} + u_{t}. \tag{3.9} xt=βft+ut.(3.9)

基于式（3.9），我们重写式（3.8）为：

y t + h = f t ′ α + ϵ ˉ t + h . (3.10) y_{t+h} = f_{t}' \alpha + \bar{\epsilon}_{t+h}. \tag{3.10} yt+h=ft′α+ϵˉt+h.(3.10)

式（3.9）与（3.10）的矩阵表示为：

X = β F + U , Y ‾ = F α + E ‾ , (3.11) X = \beta F + U, \quad \overline{Y} = F \alpha + \overline{E}, \tag{3.11} X=βF+U,Y=Fα+E,(3.11)

其中 X X X是 P × T P \times T P×T矩阵， F F F是 K × T K \times T K×T， F F F是移除最后h列的 K × ( T − h ) K \times (T - h) K×(T−h)矩阵， Y ‾ = ( y h + 1 , y h + 2 , ... , y T ) ′ \overline{Y} = (y_{h+1}, y_{h+2}, \ldots, y_{T})' Y=(yh+1,yh+2,...,yT)′， E ‾ = ( ϵ ˉ h + 1 , ϵ ˉ h + 2 , ... , ϵ ˉ T ) ′ \overline{E} = (\bar{\epsilon}{h+1}, \bar{\epsilon}{h+2}, \ldots, \bar{\epsilon}_{T})' E=(ϵˉh+1,ϵˉh+2,...,ϵˉT)′。

主成分回归（PCR）是两步程序：首先将预测变量组合为少量线性组合 f ^ t = Ω K x t \hat{f}{t} = \Omega{K} x_{t} f^t=ΩKxt，递归寻找组合权重 Ω K \Omega_{K} ΩK。第j个线性组合求解：

w j = arg ⁡ max ⁡ w ar ( x t ′ w ) , w_{j} = \arg \max_{w} \sqrt{\text{ar}}(x_{t}' w), wj=argwmaxar (xt′w),

约束为 w ′ w = 1 , Cov ^ ( x t ′ w , x t ′ w l ) = 0 , l = 1 , 2 , ... , j − 1. (3.12) w' w = 1, \quad \widehat{\text{Cov}}(x_{t}' w, x_{t}' w_{l}) = 0, \quad l = 1, 2, \ldots, j - 1. \tag{3.12} w′w=1,Cov (xt′w,xt′wl)=0,l=1,2,...,j−1.(3.12)

显然，成分选择完全不基于预测目标，而旨在最佳保留预测变量间的协方差结构。⁵ 第二步在标准预测回归（3.10）中使用估计成分 f ^ t \hat{f}_{t} f^t。

⁵该优化问题可通过 X X X的奇异值分解高效求解， X X X是以 { x 1 , ... , x T } \{x_{1}, \ldots, x_{T}\} {x1,...,xT}为列的 P × T P \times T P×T矩阵。

Stock和Watson（2002）提出基于PCR预测宏观经济变量，证明随着预测变量数P与样本量T增加，第一阶段因子恢复（至旋转）与第二阶段预测的一致性。

Ludvigson和Ng（2007）是最早使用PC预测股票收益的研究之一。其预测目标是CRSP价值加权指数的季度收益或其波动率。他们考虑两组主成分，对应构成 X X X的原始预测变量的不同选择：第一组是涵盖宏观经济各方面的指标（产出、就业、房地产、价格水平等）；第二组是包含 mostly 美国市场价格与股息数据、政府债券与信用收益率、各行业与特征组合收益的大量金融数据，共381个预测变量。他们使用BIC选择包含不同估计成分组合的模型设定。金融预测变量提取的成分对市场收益与波动率有显著样本外预测力，而宏观经济指标则无。拟合均值与波动率预测呈正相关，为市场层面的经典风险-收益权衡提供了证据。为辅助解释预测，作者指出："两个因子对季度超额收益尤为重要：与收益平方高度相关的波动率因子，以及与解释预期收益横截面差异的成熟风险因子高度相关的风险溢价因子。"

扩展其早期股票市场框架，Ludvigson和Ng（2010）使用宏观经济与金融预测变量的主成分预测国债超额收益，记录了超越远期利率（Fama和Bliss，1987；Cochrane和Piazzesi，2005）的可靠债券收益预测表现。他们强调：i) 该结果与领先的仿射期限结构模型（理论上远期利率应涵盖未来债券收益所有可预测变异）不一致；ii) 其估计的条件预期收益明显逆周期，解决了排除宏观经济成分时债券风险溢价令人困惑的周期性。

Jurado等（2015）通过PCR的巧妙应用估计宏观经济风险。其论证前提是良好的条件方差度量必须有效调整条件均值：

Var ( y t + 1 ∣ I t ) = E [ ( y t + 1 − E [ y t + 1 ∣ I t ] ) 2 ∣ I t ] . \text{Var}(y_{t+1}|\mathcal{I}{t}) = E\left[(y{t+1} - E[y_{t+1}|\mathcal{I}{t}])^{2} |\mathcal{I}{t}\right]. Var(yt+1∣It)=E[(yt+1−E[yt+1∣It])2∣It].

若均值预测程度被低估，条件风险将被高估。作者基于Ludvigson和Ng（2007，2010）的思想，用宏观经济预测变量主成分饱和市场收益（及其他宏观经济序列）的预测。由此改进的宏观经济风险估计产生有趣的经济后果：首先，高风险事件比先前认为的更少且间隔更远；其次，改进的估计揭示了风险上升与宏观经济活动低迷间更紧密的关联。

PCR仅基于预测变量间的协变构建预测变量，旨在用较少维度容纳预测变量的绝大部分变异，该步骤独立于预测阶段。这自然暗示PCR的潜在缺陷------其在降维时未考虑最终预测目标。

偏最小二乘（PLS）是PCR的替代方案，通过直接利用预测变量与预测目标间的协变降维。不同于PCR，PLS寻找与预测目标具有最大预测相关性的 X X X成分，故第j个PLS成分的权重为：

w j = arg ⁡ max ⁡ w C o v ˉ ( y t + h , x t ′ w ) 2 , w_{j} = \arg \max_{w} \bar{Cov}(y_{t+h}, x_{t}' w)^{2}, wj=argwmaxCovˉ(yt+h,xt′w)2,

约束为 w ′ w = 1 , C o v ˉ ( x t ′ w , x t ′ w l ) = 0 , l = 1 , 2 , ... , j − 1. (3.13) w' w = 1, \quad \bar{Cov}(x_{t}' w, x_{t}' w_{l}) = 0, \quad l = 1, 2, \ldots, j - 1. \tag{3.13} w′w=1,Covˉ(xt′w,xt′wl)=0,l=1,2,...,j−1.(3.13)

PLS核心是一组单变量（"偏"）模型------每次用一个预测变量预测 y t + h y_{t+h} yt+h，然后按单变量预测能力加权形成预测变量的线性组合。为构建多个PLS成分，目标与所有预测变量需相对先前构建的成分正交化，程序在正交化数据集上重复。

Kelly和Pruitt（2015）分析PLS预测模型（及称为三通回归滤波的推广）的计量特性，指出当预测变量集包含与预测无关的主导因子时PLS的韧性------此情境限制PCR的有效性。与此相关，Kelly和Pruitt（2013）基于现值恒等式分析市场收益的可预测性，指出传统现值回归（如Campbell和Shiller，1988）面临变量误差问题，提出利用PLS优势的高维回归解决方案。其分析中， Z Z Z包含大量资产的估值（账面市值比或股息价格比）横截面。施加经济约束后，他们推导出将市场收益与资产层面估值比横截面关联的现值系统。但预测变量也受预期聚合股息增长共同因子驱动。对估值比横截面应用PCR时，驱动股息增长的因子对预测市场收益无特别用处。PLS估计量学会绕过这些高方差低预测力的成分，偏好具有更强收益预测力的成分。其基于PLS的预测实现年度收益13%的样本外 R 2 R^{2} R2，为愿意择时的投资者带来巨大经济收益------相对买入持有投资者，夏普比提升超三分之一。此外，他们记录了投资者折现率的变异性远超领先理论模型的容纳范围。Chatelais等（2023）用类似框架通过资产价格横截面预测宏观经济活动，实质是执行Fama（1990）分析的PLS版本------证明资产价格领先宏观经济结果。

Baker和Wurgler（2006，2007）用PCR基于市场情绪指标预测市场收益。Huang等（2014）用PLS扩展该分析，表明PLS情绪指数相对PCR具有显著预测优势。他们认为PLS避免了Baker-Wurgler情绪代理中与测量噪声相关的常见无关因子，通过减少该噪声的混淆效应，Huang等（2014）发现情绪是预期收益的高度显著驱动因素，且此预测力大部分未被PCR检测到。类似地，Chen等（2022b）将多个投资者注意力代理组合为成功的基于PLS的市场收益预测因子。

Ahn和Bae（2022）对PLS估计量进行渐近分析，发现预测的最优PLS因子数可能远小于原始预测变量的共同因子数，且包含过多PLS因子会损害PLS预测量的样本外表现。

3.5.2 缩放PCA与监督PCA

PCR与PLS分析中便利且关键的是因子 pervasive 的假设。普遍因子模型在文献中盛行，如Bai（2003）研究 λ K ( β ′ β ) > P \lambda_{K}(\beta' \beta) \gt P λK(β′β)>P时PCA因子估计量的渐近性质。Giglio等（2022b）表明PCA与PLS预测量的表现取决于信噪比 P / ( T λ K ( β ′ β ) ) P/(T\lambda_{K}(\beta' \beta)) P/(TλK(β′β))------当 P / ( T λ K ( β ′ β ) ) ≠ 0 P/(T\lambda_{K}(\beta' \beta)) \neq 0 P/(TλK(β′β))=0时，两种预测方法通常不一致。此即弱因子问题。⁶

⁶ Bai和Ng（2021）扩展分析至适度因子（即 P / ( T λ K ( β ′ β ) ) → 0 P/(T\lambda_{K}(\beta' \beta)) \to 0 P/(TλK(β′β))→0），发现PCA保持一致性。Onatski（2009，2010，2012）的早期工作研究了因子极弱无法一致恢复的情境。

Huang等（2021）提出缩放PCA程序，根据变量与预测目标的相关性赋权后再应用PCA。该加权方案增强信噪比从而辅助因子恢复。

类似地，Giglio等（2022b）提出监督PCA（SPCA）替代方案，允许广泛因子强度谱。他们指出因子强度取决于应用PCA的变量集。SPCA包含边际筛选步骤以选择至少含一个强因子的预测变量子集，用PCA从子集提取首因子，将目标与所有预测变量（包括未选中的）投影至首因子并构建残差，随后用残差重复筛选、PCA与投影步骤，逐个提取因子直至残差与目标相关性消失。Giglio等（2022b）证明PLS与SPCA均能恢复与预测目标相关的弱因子，且所得预测量具有一致性。多目标设定中，若所有因子与至少一个预测目标相关，PLS程序能一致恢复弱因子数与整个因子空间。

3.5.3 从时间序列到面板预测

前述降维应用主要聚焦组合多预测变量预测单变量时间序列。为预测收益横截面，需将降维推广至式（3.3）的面板预测设定。类似于式（3.9）与（3.10），可写为：

R t + 1 = F t α + E t + 1 , Z t = F t γ + U t , R_{t+1} = F_{t} \alpha + E_{t+1}, \quad Z_{t} = F_{t} \gamma + U_{t}, Rt+1=Ftα+Et+1,Zt=Ftγ+Ut,

其中 R t + 1 R_{t+1} Rt+1是t+1日观测的 N × 1 N \times 1 N×1收益向量， F t F_{t} Ft是 N × K N \times K N×K矩阵， α \alpha α是 K × 1 K \times 1 K×1， E t + 1 E_{t+1} Et+1是 N × 1 N \times 1 N×1残差向量， Z t Z_{t} Zt是 N × P N \times P N×P特征矩阵， γ \gamma γ是 K × P K \times P K×P， U t U_{t} Ut是 N × P N \times P N×P残差矩阵。

随后将 { R t + 1 } , { E t + 1 } , { Z t } , { F t } , { U t } \{R_{t+1}\}, \{E_{t+1}\}, \{Z_{t}\}, \{F_{t}\}, \{U_{t}\} {Rt+1},{Et+1},{Zt},{Ft},{Ut}堆叠为 N T × 1 NT \times 1 NT×1, N T × 1 NT \times 1 NT×1, N T × P NT \times P NT×P, N T × K NT \times K NT×K, N T × P NT \times P NT×P矩阵 R ‾ \overline{R} R, E ‾ \overline{E} E, Z Z Z, F F F, U U U，使得：

R ‾ = F α + E ‾ , Z = F γ + U . \overline{R} = F \alpha + \overline{E}, \quad Z = F \gamma + U. R=Fα+E,Z=Fγ+U.

这些方程与式（3.11）形式完全相同，故前述降维程序适用。

Light等（2017）应用合并面板PLS预测股票收益，Gu等（2020b）用合并面板PCA与PLS预测个股收益。Gu等（2020b）基于PCA与PLS的等权重多空组合年化夏普比分别为1.89与1.47，优于基于弹性网络的组合。

3.5.4 主组合

Kelly等（2020a）提出收益预测与组合优化的不同降维方法"主组合分析"（PPA）。前文框架中，高维性源于每项资产有许多潜在预测变量。实证资产定价多数模型聚焦自有资产预测信号------即 S i , t S_{i,t} Si,t仅与资产i的收益 R i , t + 1 R_{i,t+1} Ri,t+1的关联。PPA动机在于希望同时利用多资产的联合预测信息，借助所有资产的预测信号预测其他所有资产的收益。此时高维性源于潜在交叉预测关系的庞大数量。

简言之，假设每项资产有单一信号 S i , t S_{i,t} Si,t（堆叠为N维向量 S t S_{t} St）。PPA始于所有资产未来收益与所有资产信号的交叉协方差矩阵：

Π = E ( R t + 1 S t ′ ) ∈ R N × N . \Pi = E(R_{t+1}S_{t}') \in \mathbb{R}^{N \times N}. Π=E(Rt+1St′)∈RN×N.

Kelly等（2020a）称 Π \Pi Π为"预测矩阵"。其对角线部分追踪自有信号预测效应（传统收益预测模型焦点），非对角线追踪交叉预测现象。

PPA对预测矩阵应用SVD。Kelly等（2020a）证明 Π \Pi Π的奇异向量（那些主导信号与未来收益协变的向量）是一组标准化投资组合，按从最可被 S S S预测到最不可预测排序。

领先奇异向量是"主组合"。Kelly等（2020a）表明主组合可直接解释为最优组合------具体而言，它们是基于信号 S S S最"可定时"的组合，为面临杠杆约束（即不能持有任意大头寸）的投资者提供最高平均收益。

Kelly等（2020a）还指出 Π \Pi Π编码了关于资产定价模型与定价误差的有用信息。为梳理与beta versus alpha相关的收益预测，可将 Π \Pi Π分解为对称部分（ Π s \Pi^{s} Πs）与反对称部分（ Π a \Pi^{a} Πa）：

Π = 1 2 ( Π + Π ′ ) ⏟ Π s + 1 2 ( Π − Π ′ ) ⏟ Π a . (3.14) \Pi = \underbrace{\frac{1}{2}(\Pi + \Pi')}{\Pi^{s}} + \underbrace{\frac{1}{2}(\Pi - \Pi')}{\Pi^{a}}. \tag{3.14} Π=Πs 21(Π+Π′)+Πa 21(Π−Π′).(3.14)

Kelly等（2020a）证明 Π a \Pi^{a} Πa的领先奇异向量（"主alpha组合"）可解释为纯alpha策略，而 Π s \Pi^{s} Πs的为纯beta组合（"主暴露组合"）。因此，Kelly等（2020a）提出基于主alpha组合平均收益的资产定价模型新检验（作为Gibbons等（1989）等检验的替代）。虽然Kelly等（2020a）聚焦每资产单一信号情形，He等（2022b）展示了如何可扩展至多信号。Goulet Coulombe和Gobel（2023）通过随机森林与约束岭回归组合，处理与Kelly等（2020a）相似的问题------构建最大可预测组合。

Kelly等（2020a）将PPA应用于多资产类别数据集。图3.3展示其分析一例：资产集 R t + 1 R_{t+1} Rt+1为25个Fama-French规模与账面市值比组合，信号 S t S_{t} St为各资产的时间序列动量。图显示所得主组合的大样本外夏普比，及其相对包含五因子Fama-French模型加标准时间序列动量因子的基准模型产生显著alpha。

图3.3：主组合表现比率

3.6 决策树

现代资产定价模型（含习惯持续、长期风险或时变灾难风险）具有金融市场行为的高度状态依赖性，表明交互效应可能对实证模型很重要。例如Hong等（2000）构建信息理论，其中动量效应由公司规模与分析覆盖率调节，强调预期股票收益随公司特征交互作用而变化。概念上，在线性模型中引入变量交互即可纳入此类效应，如同式（3.5）引入非线性变换。但缺乏关于相关交互的先验假设时，此广义加性方法会快速遭遇计算限制------多向交互组合性增加参数数量。⁷

⁷ 如Gu等（2020b）指出："当预测变量数指数级多于观测数时，参数惩罚无法解决线性模型估计难题，必须转向启发式优化算法如逐步回归（依停止规则序贯增删变量）、变量筛选（保留与预测目标单变量相关性超阈值的预测变量）等。"

回归树提供以更低计算成本纳入多向预测变量交互的途径。树将数据观测划分为共享共同特征交互的组，逻辑是通过寻找同质观测组，可用该组历史数据预测新进入组的观测行为。图3.4展示含"规模"与"账面市值比"两预测变量的示例。左图描述树如何根据预测变量值分配各观测至分区：首先按规模排序，高于0.5断点的分入类别3；小规模观测再按账面市值比排序，低于0.3的分入类别1，高于0.3的分入类别2。最后，各分区观测的预测定义为该分区结果变量值的简单平均。

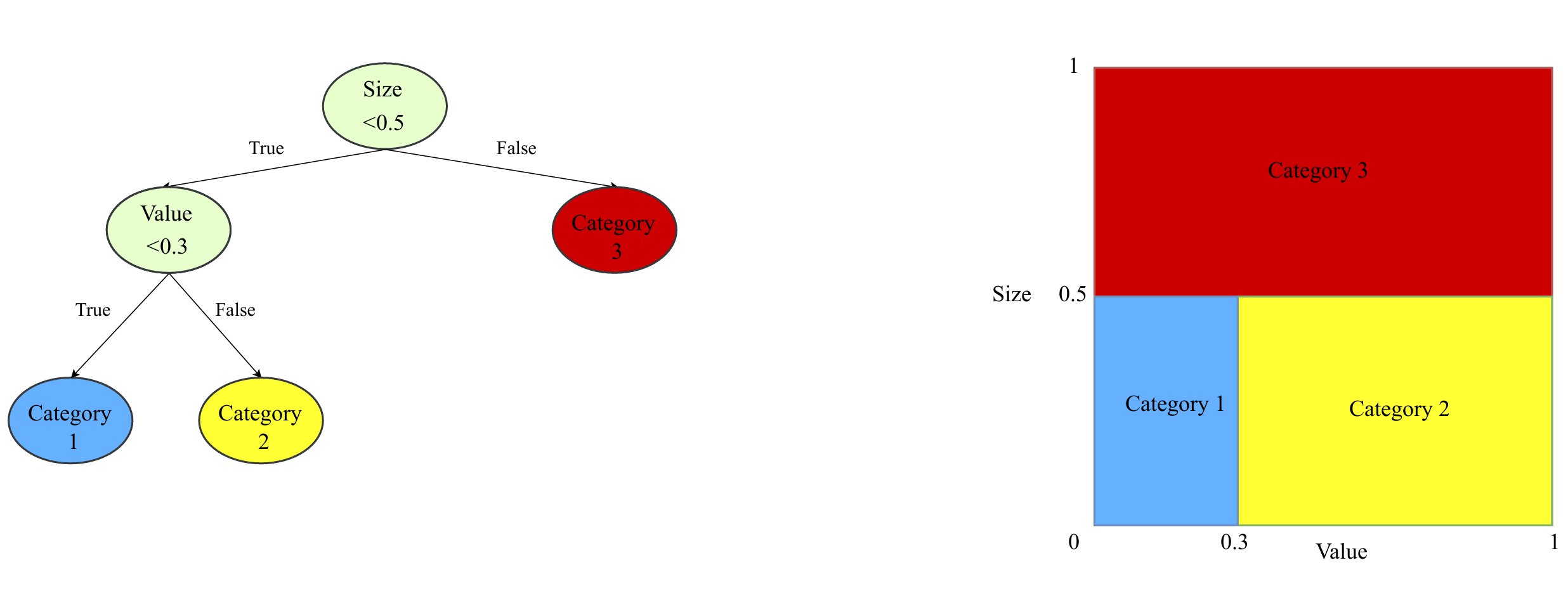
图4：回归树示例

注：左图展示回归树图示，右图展示两特征（规模与价值）空间中对应的分区表示。树的终端节点分别以蓝、黄、红色标示。基于这两特征的值，个股样本被划分为三类。

含 K K K个"叶"（终端节点）与深度 L L L的树的通用预测函数为：

g ( z i , t ; θ , K , L ) = ∑ k = 1 K θ k 1 { z i , t ∈ C k ( L ) } , (3.15) g(z_{i,t};\theta,K,L) = \sum_{k=1}^{K} \theta_k \mathbf{1}{\{z{i,t} \in C_k(L)\}}, \tag{3.15} g(zi,t;θ,K,L)=k=1∑Kθk1{zi,t∈Ck(L)},(3.15)

其中 C k ( L ) C_k(L) Ck(L)是 K K K个分区之一。每个分区是最多 L L L个指示函数的乘积。与分区 k k k关联的常数参数 θ k \theta_k θk估计为该分区结果变量的样本均值。

决策树的流行性更多源于其"贪婪"算法能有效隔离高预测力分区且计算成本低，而非其结构。虽然分支划分的具体预测变量（及划分值）选择以最小化预测误差为目标，但可能划分空间如此广阔以致树无法全局优化，划分是短视确定的，估计树是对不可行最优树模型的粗糙近似。

树灵活容纳交互（深度 L L L的树可捕捉 ( L − 1 ) (L-1) (L−1)-way交互）但易过拟合。为抵消此倾向，树通常以正则化"集成"形式使用。常见集成方法为"提升"（梯度提升回归树，"GBRT"）------递归组合多个浅层弱预测树的预测形成单一强预测器（见Schapire，1990；Friedman，2001）。提升程序始于拟合浅树（如深度 L = 1 L=1 L=1），随后第二棵简单树拟合首树的预测残差，第二树预测以因子 ν ∈ ( 0 , 1 ) \nu \in (0,1) ν∈(0,1)收缩后加入首树预测。收缩有助于防止模型过拟合前树残差。此过程迭代形成 B B B棵浅树的加性集成。提升集成因而有三个调参参数 ( L , ν , B ) (L,\nu,B) (L,ν,B)。

Rossi和Timmermann（2015）研究Merton（1973）的ICAPM，评估条件股票风险溢价是否随市场对经济状态变量的暴露变化。此研究关键在于ICAPM条件协方差的准确测度。为此，作者用提升树预测经济活动日度指数与市场组合日收益的已实现协方差，预测变量包括Welch和Goyal（2008）的宏观金融数据序列及过去已实现协方差。与传统文献不同，这些条件协方差估计与条件股票风险溢价呈显著正时序关联，且暗示投资者风险厌恶的经济合理幅度。作者表明条件协方差的线性模型设定严重错误，这可能是先前ICAPM检验结果混杂的原因。他们将关于ICAPM的积极结论归因于提升树方法------其非线性灵活性减少了条件协方差函数的设定误差。

Rossi（2018）在相关工作中用宏观金融预测变量的提升回归树直接预测月度股票总收益（及波动率），但不强加ICAPM通过条件方差及与经济状态变量协方差引入预测的限制。他表明提升树预测的月收益样本外 R 2 R^2 R2为0.3%（相比历史均值收益预测的-0.7%），月方向准确性57.3%。这导致相对市场买入持有策略的显著样本外alpha，对应风险厌恶为二的均值-方差投资者30%效用增益。

第二种流行的树正则器是"随机森林"模型，类似提升，它从多棵浅树创建预测集成。遵循Breiman（2001）更通用的"装袋"（自助聚合）程序，随机森林从数据中抽取 B B B个自助样本，对每样本拟合独立回归树后平均其预测。除通过自助随机化估计样本外，随机森林还随机化建树可用的预测变量集（称为"丢弃"）。装袋与丢弃均正则化随机森林预测。单棵树的深度 L L L、自助样本数 B B B及丢弃率为调参参数。

基于树的收益预测与资产定价文献中的条件（序贯）排序同构。考虑规模与价值信号的三分位序贯排序生成九组双重排序组合，这是首层分割点为规模分布三分位数、次层为价值分布三分位数的两层三元决策树。树的每个叶 j j j可解释为组合------其t时刻收益为t时刻分配至叶 j j j的所有股票收益的（加权）平均。类似地，叶 j j j中每只股票的预测为训练集中分配至 j j j的股票收益均值。

受此同构启发，Moritz和Zimmermann（2016）通过从大量股票特征估计回归树进行条件组合排序，而非使用预定义的排序变量与断点。传统排序至多容纳两三个股票信号交互，而树能更广泛搜索最具预测力的多向交互。他们不进行单次树排序，而用随机森林从200棵树产生集成收益预测。作者报告基于一月前瞻随机森林预测的等权重多空十分位差策略月收益2.3%（但作者也表明该表现严重受交易成本高昂的月反转信号影响）。

基于Moritz和Zimmermann（2016），Bryzgalova等（2020）用"AP-tree"方法进行组合排序。Moritz和Zimmermann（2016）强调树排序的收益预测力，Bryzgalova等（2020）则强调排序组合本身作为评估资产定价模型的测试资产的有用性。AP-tree不同于传统树模型------它不学习树结构本身，而是用预选信号顺序的中位数分割生成。图3.5左展示对指定首按中位价值、再按中位价值（即生成四分位分割）、最后按中位公司规模分割的三层树。AP-tree按全局夏普比准则引入"剪枝"：从预定树结构中，每个节点代表组合，AP-tree程序找到节点组合的均值-方差有效组合，对组合权重施加弹性网络惩罚。最终，程序丢弃交叉验证优化中权重为零的节点，存活节点组合用作辅助资产定价分析的测试资产。作者对多组三重信号重复此分析，构建多种剪枝AP-tree作为测试资产。Bryzgalova等（2020）强调其优化组合作为候选随机折现因子的可行性，将其与第5.5节文献关联。⁸

⁸ Giglio等（2021b）指出测试资产选择是弱因子的补救措施，故无剪枝构建AP-tree也是构建多组分散化组合作为测试资产的合理方案，可筛选构建弱因子的对冲组合。

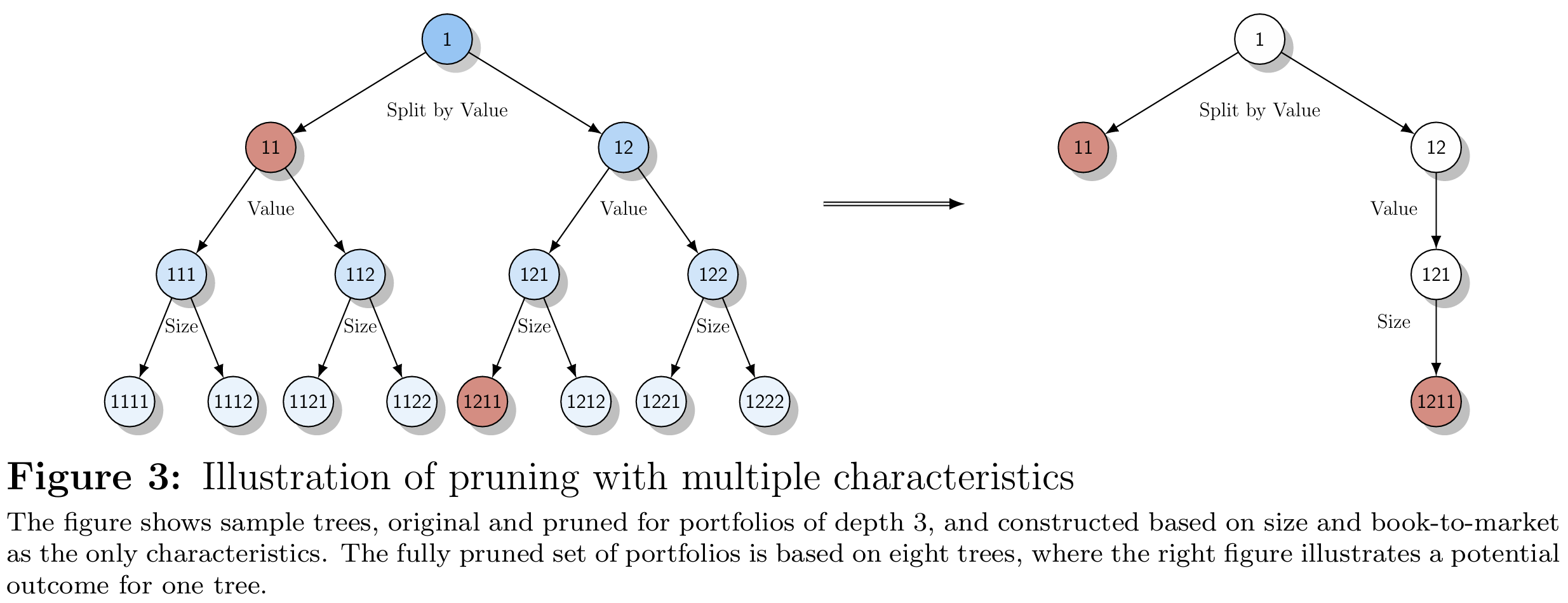
图5：来源：Bryzgalova等（2020）

该图展示基于规模与账面市值比作为唯二特征构建的深度3组合的样本树（原始与剪枝后），右图展示一棵树的可能结果。

Cong等（2022）通过引入面板树（P-Tree）模型推动资产定价树方法前沿，该模型基于公司特征分割股票收益横截面以开发条件资产定价模型。每次分割，算法从特征池（标准化至-1到1范围）与预定分割阈值集（如-0.6, -0.2, 0.2, 0.6）选择分割规则候选（如规模<0.2）形成子叶，每叶代表收益组合。他们提出基于资产定价目标的有说服力的分割准则。当预定的最小叶规模或最大叶数满足时，P-tree算法终止。P-tree程序产生保留可解释性与灵活性的单树结构单因子条件资产定价模型。

树方法还用于收益预测外的多种金融预测任务。我们简要讨论三例：信用风险预测、流动性预测与波动率预测。Correia等（2018）用基本分类树预测信用事件（破产与违约），发现广泛的公司风险特征提升预测准确性，其模型相对传统信用风险模型（如Altman，1968；Ohlson，1980）展示更优样本外分类准确率。Easley等（2020）在真正的大数据环境------87个期货市场的tick数据中，用随机森林模型研究流动性与风险的高频动态，表明多种市场流动性指标（如Kyle's lambda、Amihud指标、知情交易概率）对后续风险与流动性结果（包括买卖价差、收益波动率与收益偏度）的方向变动具有实质预测力。Mittnik等（2015）用提升树预测月度股市波动率，以84个宏观金融时间序列为预测变量，通过提升递归构建优化月度收益高斯对数似然的波动率预测树集成，发现相对GARCH与EGARCH基准模型，树基波动率预测大幅显著降低预测误差。

3.7 普通神经网络

神经网络或许是机器学习中最受欢迎且最成功的模型。其理论根基是"通用逼近器"，可逼近任何光滑预测函数（Hornik等，1989；Cybenko，1989），但缺乏透明性与可解释性。

Gu等（2020b）分析"前馈"网络的预测。我们详述此结构，因其为后续更复杂架构（如循环与卷积网络）奠定基础。这些网络包含原始预测变量的"输入层"、交互并非线性变换预测变量的一或多个"隐藏层"，以及将隐藏层聚合为最终结果预测的"输出层"。

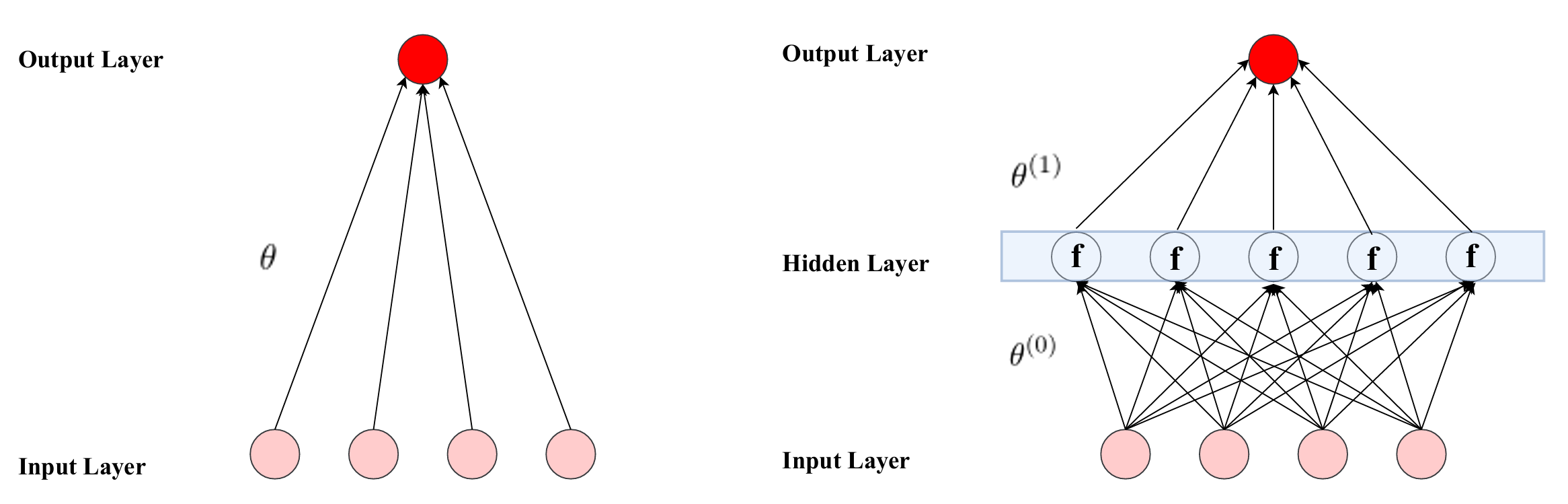
图6：神经网络

注 ：该图展示两个简单神经网络图示，含（右）或不含（左）隐藏层。粉色圆圈表示输入层，深红圆圈表示输出层。每条箭头关联一个权重参数。含隐藏层的网络中，非线性激活函数 f f f变换输入后传递至输出。

图3.6左展示无隐藏层的极简网络。预测变量（标为 z 1 , . . . , z 4 z_1, ..., z_4 z1,...,z4）由包含截距与每预测变量一权重参数的向量（ θ \theta θ）加权，这些权重将信号聚合为预测 θ 0 + ∑ k = 1 4 z k θ k \theta_0 + \sum_{k=1}^4 z_k \theta_k θ0+∑k=14zkθk。如例所示，无中间节点时神经网络即线性回归模型。

右图引入含五个神经元的隐藏层。神经元接收预测变量的线性组合，通过非线性"激活函数" f f f馈送，输出传递至下一层。例如第二神经元输出为 x 2 ( 1 ) = f ( θ 2 , 0 ( 0 ) + ∑ j = 1 4 z j θ 2 , j ( 0 ) ) x^{(1)}2 = f \left( \theta^{(0)}{2,0} + \sum_{j=1}^4 z_j \theta^{(0)}_{2,j} \right) x2(1)=f(θ2,0(0)+∑j=14zjθ2,j(0))。此例中，各神经元结果线性聚合为最终输出预测：

g ( z ; θ ) = θ 0 ( 1 ) + ∑ j = 1 5 x j ( 1 ) θ j ( 1 ) g(z; \theta) = \theta^{(1)}0 + \sum{j=1}^5 x^{(1)}{j} \theta^{(1)}{j} g(z;θ)=θ0(1)+j=1∑5xj(1)θj(1)

非线性激活函数选择多样（如sigmoid、正弦、双曲、softmax、ReLU等）。"深度"前馈网络通过引入额外隐藏层，将前隐藏层的非线性变换以线性组合并再次非线性激活，此迭代非线性复合产生更丰富、更高参数化的近似模型。

如Gu等（2020b），深度前馈神经网络的一般公式如下：设 K ( l ) K^{(l)} K(l)表示每层 l = 1 , . . . , L l = 1, ..., L l=1,...,L的神经元数。定义层 l l l中神经元 k k k的输出为 x k ( l ) x_{k}^{(l)} xk(l)，增强含常数 x 0 ( l ) x_{0}^{(l)} x0(l)的该层输出向量为 x ( l ) = ( 1 , x 1 ( l ) , . . . , x K ( l ) ( l ) ) ′ x^{(l)} = (1, x_{1}^{(l)}, ..., x_{K^{(l)}}^{(l)})' x(l)=(1,x1(l),...,xK(l)(l))′。初始化网络时，类似定义输入层为原始预测变量 x ( 0 ) = ( 1 , z 1 , . . . , z N ) ′ x^{(0)} = (1, z_{1}, ..., z_{N})' x(0)=(1,z1,...,zN)′。神经网络在每层 l > 0 l > 0 l>0各神经元的递归输出公式为：

x k ( l ) = f ( x ( l − 1 ) ′ θ k ( l − 1 ) ) , (3.16) x_{k}^{(l)} = f \left( x^{(l-1)'} \theta_{k}^{(l-1)} \right), \tag{3.16} xk(l)=f(x(l−1)′θk(l−1)),(3.16)

最终输出为：

g ( z ; θ ) = x ( L − 1 ) ′ θ ( L − 1 ) . (3.17) g(z; \theta) = x^{(L-1)'} \theta^{(L-1)}. \tag{3.17} g(z;θ)=x(L−1)′θ(L−1).(3.17)

每隐藏层 l l l的权重参数数为 K ( l ) ( 1 + K ( l − 1 ) ) K^{(l)} (1 + K^{(l-1)}) K(l)(1+K(l−1))，输出层另需 1 + K ( L − 1 ) 1 + K^{(L-1)} 1+K(L−1)个权重。Gu等（2020b）的五层网络含30,185个参数。

Gu等（2020b）估计1957至2016年CRSP样本的月度股票面板预测模型，原始特征包括94个秩标准化股票特征与8个宏观金融时间序列的交互及74个行业指标，共920个特征。他们通过分析含1至5个隐藏层网络（标记为NN1至NN5）的表现，推断网络深度在收益预测问题中的权衡。NN1、NN3、NN5模型的月样本外预测 R 2 R^{2} R2分别为0.33%、0.40%、0.36%，而Lewellen（2015）倡导的三信号（规模、价值、动量）线性模型基准为0.16%。对NN3模型，大市值股的 R 2 R^{2} R2显著更高达0.70%，表明机器学习不仅捕捉流动性驱动的小规模低效。预测年度而非月度收益时，样本外 R 2 R^{2} R2升至3.40%，显示神经网络还能分离持续于商业周期频率的可预测模式。

	NN1	NN1	NN1	NN1	NN3	NN3	NN3	NN3	NN5	NN5	NN5	NN5
	预测	平均	标准差	夏普比	预测	平均	标准差	夏普比	预测	平均	标准差	夏普比
面板A：等权重
低(L)	-0.45	-0.78	7.43	-0.36	-0.31	-0.92	7.94	-0.40	-0.08	-0.83	7.92	-0.36
2	0.15	0.22	6.24	0.12	0.22	0.16	6.46	0.09	0.33	0.24	6.64	0.12
3	0.43	0.47	5.55	0.29	0.45	0.44	5.40	0.28	0.51	0.53	5.65	0.32
4	0.64	0.64	5.00	0.45	0.60	0.66	4.83	0.48	0.62	0.59	4.91	0.41
5	0.80	0.80	4.76	0.58	0.73	0.77	4.58	0.58	0.71	0.68	4.56	0.51
6	0.95	0.85	4.63	0.63	0.85	0.81	4.47	0.63	0.80	0.76	4.43	0.60
7	1.12	0.84	4.66	0.62	0.97	0.86	4.62	0.64	0.88	0.88	4.60	0.66
8	1.32	0.88	4.95	0.62	1.12	0.93	4.82	0.67	1.01	0.95	4.90	0.67
9	1.63	1.17	5.62	0.72	1.38	1.18	5.51	0.74	1.25	1.17	5.60	0.73
高(H)	2.43	2.13	7.34	1.00	2.28	2.35	8.11	1.00	2.08	2.27	7.95	0.99
H-L	2.89	2.91	4.72	2.13	2.58	3.27	4.80	2.36	2.16	3.09	4.98	2.15
面板B：市值加权
低(L)	-0.38	-0.29	7.02	-0.14	-0.03	-0.43	7.73	-0.19	-0.23	-0.51	7.69	-0.23
2	0.16	0.41	5.89	0.24	0.34	0.30	6.38	0.16	0.23	0.31	6.10	0.17
3	0.44	0.51	5.07	0.35	0.51	0.57	5.27	0.37	0.45	0.54	5.02	0.37
4	0.64	0.70	4.56	0.53	0.63	0.66	4.69	0.49	0.60	0.67	4.47	0.52
5	0.80	0.77	4.37	0.61	0.71	0.69	4.41	0.55	0.73	0.77	4.32	0.62
6	0.95	0.78	4.39	0.62	0.79	0.76	4.46	0.59	0.85	0.86	4.38	0.68
7	1.11	0.81	4.40	0.64	0.88	0.99	4.77	0.72	0.96	0.88	4.76	0.64
8	1.31	0.75	4.86	0.54	1.00	1.09	5.47	0.69	1.11	0.94	5.17	0.63
9	1.58	0.96	5.22	0.64	1.21	1.25	5.94	0.73	1.34	1.02	6.02	0.58
高(H)	2.19	1.52	6.79	0.77	1.83	1.69	7.29	0.80	1.99	1.46	7.40	0.68
H-L	2.57	1.81	5.34	1.17	1.86	2.12	6.13	1.20	2.22	1.97	5.93	1.15

表3.3 ：机器学习组合表现
注：本表报告1987-2016测试期（1957-1974训练、1975-1986验证）基于预测排序组合的表现。所有股票按次月预测收益分为十分位。"预测"、"平均"、"标准差"、"夏普比"列分别提供各十分位的预测月收益、实现平均月收益、标准差及夏普比。

接着，Gu等（2020b）报告基于神经网络月收益预测的十分位组合排序，重现于表3.3。面板A报告等权平均收益，面板B报告市值加权收益。样本外组合收益跨十分位单调递增。神经网络预测收益与实现平均收益的定量匹配令人印象深刻。多空十分位差策略的年化等权夏普比NN1、NN3、NN5分别为2.1、2.4、2.2，三者的市值加权夏普比均为1.2。因此，尽管大市值股的收益预测 R 2 R^2 R2更高，但神经网络模型的收益预测内容在交易小股票时尤其有利可图。Avramov等（2022a）通过更彻底的套利限制调查证实该发现，证明神经网络预测在难估值与难套利股票中最成功。他们发现，调整交易成本与其他实际考量后，基于神经网络的策略相对典型基准仍显著有益------盈利性高（尤其多头头寸）、下行风险小且在近期数据中持续表现良好。

作为参照，Gu等（2020b）复现Lewellen（2015）三信号线性模型的等权夏普比为0.8（市值加权0.6），这本身令人印象深刻，但神经网络预测的大幅改进强调了非线性和交互在预期收益模型中的重要作用。Gu等（2020b）的图3.7通过绘制模型中少数特征的效应说明该事实，展示当固定其他变量为中值时，成对特征在其支持[-1,1]上变化时期望收益如何变化。报告效应是股票规模（mwell）与短期反转（mom1m）、动量（mom12m）、总波动率（retvol）及应计（acc）的交互。例如左上图显示，小股票（蓝线）的短期反转效应最强且基本线性，而超大市值股（绿线）的反转效应呈凹形，在过往超大市值股收益强劲为正时表现最突出。

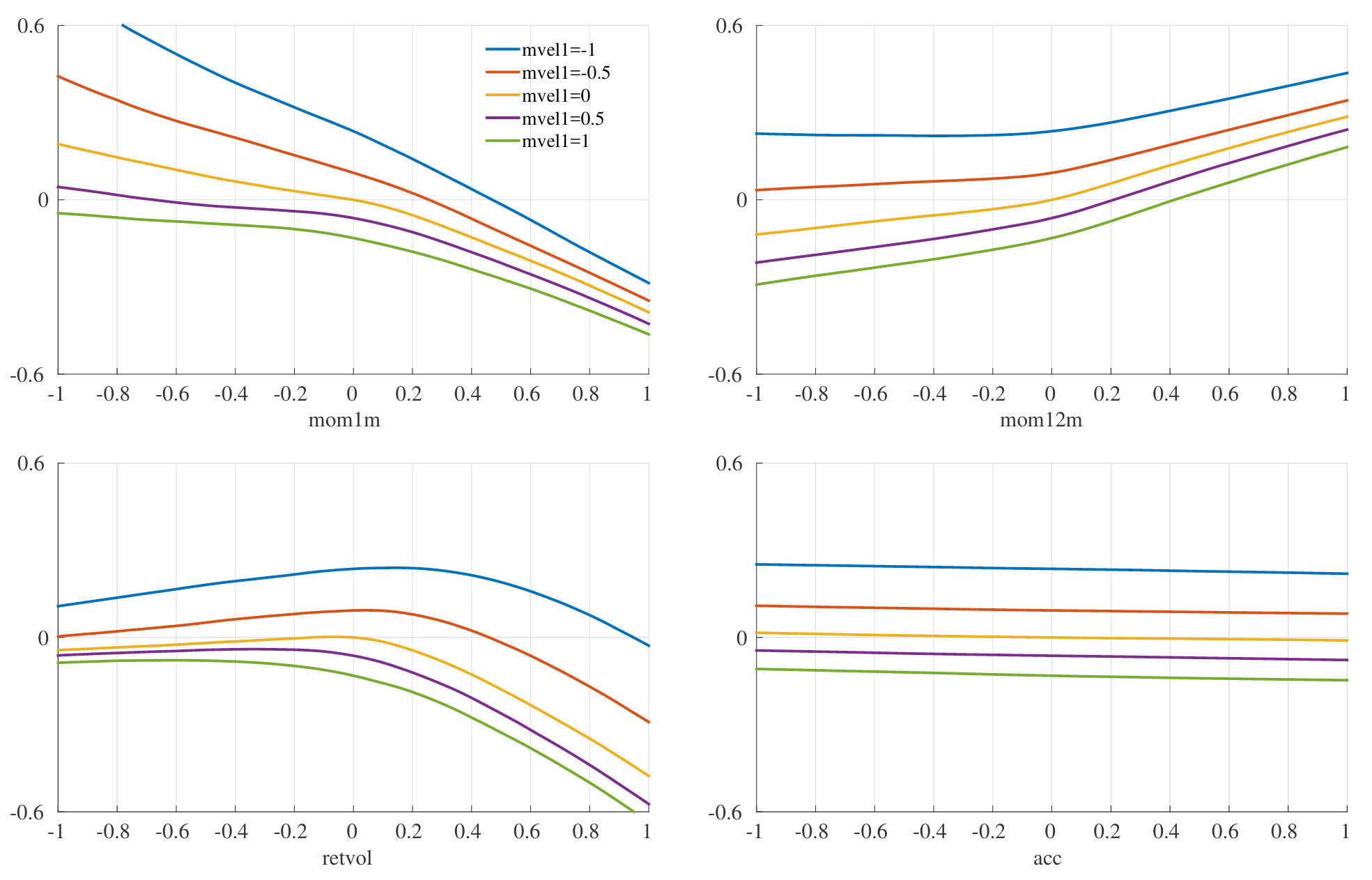
图7：期望收益与特征交互（NN3）

注：模型NN3中期望月百分比收益（纵轴）对mvel1与mom1m、mom12m、retvol、acc交互效应的敏感性（其他协变量固定为中值）。

Gu等（2020b）的模型应用于股票层面面板。Feng等（2018）用纯时间序列前馈网络基于Welch-Goyal宏观金融预测变量预测市场总收益，发现相对线性模型（含惩罚与降维）的样本外 R 2 R^2 R2显著提升。

3.8 比较分析

	OLS	OLS-3	PLS	PCR	ENet	GLM	RF	GBRT	NN1	NN2	NN3	NN4	NN5
	+H	+H			+H	+H		+H
全样本	-3.46	0.16	0.27	0.26	0.11	0.19	0.33	0.34	0.33	0.39	0.40	0.39	0.36
前1000	-11.28	0.31	-0.14	0.06	0.25	0.14	0.63	0.52	0.49	0.62	0.70	0.67	0.64
后1000	-1.30	0.17	0.42	0.34	0.20	0.30	0.35	0.32	0.38	0.46	0.45	0.47	0.42

表3.4 ：股票层面月样本外预测表现（百分比 R o o s 2 R^{2}_{oos} Roos2）

注：Gu等（2020b）报告全股票面板的月 R o o s 2 R^{2}{oos} Roos2，比较使用所有变量的OLS（OLS）、仅用规模、账面市值比与动量的OLS（OLS-3）、PLS、PCR、弹性网络（ENet）、广义线性模型（GLM）、随机森林（RF）、梯度提升回归树（GBRT）及1至5层神经网络（NN1--NN5）。"+H"表示使用Huber损失替代 l 2 l_2 l2损失。 R o o s 2 R^{2}{oos} Roos2也报告于仅含市值前1000或后1000股票的子样本。

近期多篇论文在不同数据集比较机器学习收益预测模型。首项此类研究Gu等（2020b）在股票-月度面板预测设定中比较上述主要机器学习方法。表3.4重现其关于跨模型样本外面板收益预测 R 2 R^{2} R2的主要结果。该比较分析帮助确立金融机器学习多项新实证事实：首先，多预测变量的简单线性模型（表中"OLS"）预测准确性受损，未能超越零预测的朴素基准。Gu等（2020b）将预测 R 2 R^{2} R2定义为相对零预测而非更传统的历史样本均值收益基准，指出：

"用历史平均超额股票收益预测未来表现通常大幅_逊于_零预测的朴素基准。即历史平均股票收益噪声过大，人为降低了'良好'预测表现的门槛。我们通过以零预测为基准避免此陷阱。为说明此选择的重要性，当我们以历史平均股票收益为基准时，所有方法的月样本外 R 2 R^{2} R2提升约三个百分点。"⁹
⁹ He等（2022a）提出使用横截面均值收益作为朴素基准的替代横截面样本外 R 2 R^{2} R2。

通过降维或收缩正则化将线性模型的 R 2 R^{2} R2提升至约0.3%/月。非线性模型（尤其神经网络）进一步帮助，尤其在大市值股中。非线性模型优于仅使用文献中三个精选预测信号的线性模型（表中"OLS-3"）。

非线性模型在经济术语中也提供大增量收益。表3.5重现Gu等（2020b）的表8，显示各模型收益预测排序多空十分位差策略的样本外表现。首先值得注意的是，样本外 R 2 R^{2} R2相对较小的模型产生显著交易收益（相对Fama-French六因子模型（含动量因子）的alpha与信息比）。这与Kelly等（2022a）的观点一致------ R 2 R^{2} R2是收益预测经济价值的不可靠诊断；他们建议基于经济标准（如交易策略夏普比）评判金融机器学习方法。表3.5中非线性模型在交易策略表现方面提供最佳经济价值。

	OLS-3	PLS	PCR	ENet	GLM	RF	GBRT	NN1	NN2	NN3	NN4	NN5
	+H			+H	+H		+H
风险调整表现（市值加权）
平均收益	0.94	1.02	1.22	0.60	1.06	1.62	0.99	1.81	1.92	1.97	2.26	2.12
FF5+Mom α \alpha α	0.39	0.24	0.62	-0.23	0.38	1.20	0.66	1.20	1.33	1.52	1.76	1.43
t值	2.76	1.09	2.89	-0.89	1.68	3.95	3.11	4.68	4.74	4.92	6.00	4.71
R 2 R^2 R2	78.60	34.95	39.11	28.04	30.78	13.43	20.68	27.67	25.81	20.84	20.47	18.23
信息比	0.54	0.21	0.57	-0.17	0.33	0.77	0.61	0.92	0.93	0.96	1.18	0.92
风险调整表现（等权重）
平均收益	1.34	2.08	2.45	2.11	2.31	2.38	2.14	2.91	3.31	3.27	3.33	3.09
FF5+Mom α \alpha α	0.83	1.40	1.95	1.32	1.79	1.88	1.87	2.60	3.07	3.02	3.08	2.78
t( α \alpha α)	6.64	5.90	9.92	4.77	8.09	6.66	8.19	10.51	11.66	11.70	12.28	10.68
R 2 R^2 R2	84.26	26.27	40.50	20.89	21.25	19.91	11.19	13.98	10.60	9.63	11.57	14.54
信息比	1.30	1.15	1.94	0.93	1.58	1.30	1.60	2.06	2.28	2.29	2.40	2.09

表3.5：机器学习组合的风险调整表现、回撤与换手率

注 ：表格报告平均月收益百分比，以及相对Fama-French五因子模型（增补动量因子）的alpha、信息比（IR）与 R 2 R^2 R2。

后续论文在其他资产类别进行类似比较分析。Choi等（2022）在国际股票市场分析Gu等（2020b）的相同模型，得出非线性模型表现最佳的相似结论。有趣的是，他们证明了迁移学习的可行性------在美国数据训练的模型用于预测国际股票收益时仍具显著样本外表现。相关地，Jiang等（2018）用PCR与PLS发现中国股票收益与公司特征间基本相似的模式。近期Leippold等（2022）比较预测中国股票收益的机器学习模型，强调流动性、散户参与及国有企业在国内市场行为的突出作用。

Ait-Sahalia等（2022）研究高频收益（及久期、成交量等其他量）的机器学习预测，构建13个预测变量在9个时间窗口的117个变量，实验两年期的S&P 100指数成分股，发现除OLS外所有方法表现非常相似。对多数案例，随机森林或提升树等非线性方法相对lasso的改进有限。

Bali等（2020）与He等（2021）比较美国公司债收益预测的机器学习方法。Bali等（2020）的预测信号包括43个债券特征（如发行规模、信用评级、久期等），研究模型与Gu等（2020b）相同外加LSTM网络（下小节讨论）。表3.6报告Bali等（2020）结果，其关于预测 R 2 R^{2} R2与十分位差组合收益的机器学习模型比较大体支持Gu等（2020b）结论：无正则线性模型表现最差，惩罚与降维显著改进线性模型表现，非线性模型总体最佳。

	OLS	PCA	PLS	Lasso	Ridge	ENet	RF	FFN	LSTM	组合
R o o s 2 R^2_{oos} Roos2	-3.36	2.07	2.03	1.85	1.89	1.87	2.19	2.37	2.28	2.09
平均收益	0.16	0.51	0.63	0.39	0.33	0.43	0.79	0.75	0.79	0.67

表3.6：机器学习比较债券收益预测（Bali等，2020）

注：首行报告基于43个债券特征（来自Bali等（2020）表2）的全债券面板样本外 R 2 R^2 R2百分比。次行报告基于机器学习收益预测排序的市值加权十分位差债券组合的平均样本外月收益百分比（来自Bali等（2020）表3）。

此外，Bali等（2020）研究尊重公司股权与债务价格无套利隐含一致性的机器学习预测框架，允许跨资本结构形成预测------利用股权信息预测债券收益。他们发现：

"一旦施加Merton（1974）模型结构，股权特征对债券未来收益的增量预测力显著超越债券特征，而在无此经济结构的简化形式方法中，股权特征对债券收益的增量预测力相当有限。"

这是机器学习与经济结构互补性的佳例，呼应Israel等（2020）的论点。

最后，Bianchi等（2021）比较预测美国政府债券收益的机器学习模型。这是纯时间序列环境（相较前述研究面板收益数据的比较分析），但仍得出惩罚与降维线性模型优于无约束线性模型、非线性模型优于线性模型的相似结论。

3.9 更复杂的神经网络

循环神经网络（RNN）是捕捉序列数据复杂动态的流行模型。本质上是高度参数化的非线性状态空间模型，使其自然成为时间序列预测的候选者。RNN的有前景用途是将式（3.2）的限制性模型设定推广至捕捉收益与特征间的长期依赖。具体而言，我们考虑股票i在时间t的预期收益的一般循环模型：

E t [ R i , t + 1 ] = g ∗ ( h i , t ) , (3.18) E_t [R_{i,t+1}] = g^*(h_{i,t}), \tag{3.18} Et[Ri,t+1]=g∗(hi,t),(3.18)

其中 h i , t h_{i,t} hi,t是依赖于 z i , t z_{i,t} zi,t及其历史值的隐藏状态变量向量。

经典RNN假设：

g ∗ ( h i , t ) = σ ( c + V h i , t ) , h i , t = tanh ⁡ ( b + W h i , t − 1 + U z i , t ) , g^*(h_{i,t}) = \sigma (c + V h_{i,t}), \quad h_{i,t} = \tanh(b + W h_{i,t-1} + U z_{i,t}), g∗(hi,t)=σ(c+Vhi,t),hi,t=tanh(b+Whi,t−1+Uzi,t),

其中 b , c , U , V b, c, U, V b,c,U,V, W W W为未知参数， σ ( ⋅ ) \sigma(\cdot) σ(⋅)为sigmoid函数。上式仅含一层隐藏状态，可堆叠多层隐藏状态构建容纳更复杂序列的深度RNN。例如可写 h i , t ( 0 ) = z i , t h_{i,t}^{(0)} = z_{i,t} hi,t(0)=zi,t，对 1 ≤ l ≤ L 1 \leq l \leq L 1≤l≤L有：

g ∗ ( h i , t ( L ) ) = σ ( c + V h i , t ( L ) ) , h i , t ( l ) = tanh ⁡ ( b + W h i , t − 1 ( l ) + U h i , t ( l − 1 ) ) . g^*(h_{i,t}^{(L)}) = \sigma(c + Vh_{i,t}^{(L)}), \quad h_{i,t}^{(l)} = \tanh(b + Wh_{i,t-1}^{(l)} + Uh_{i,t}^{(l-1)}). g∗(hi,t(L))=σ(c+Vhi,t(L)),hi,t(l)=tanh(b+Whi,t−1(l)+Uhi,t(l−1)).

经典RNN难以捕捉长期依赖------其套叠结构暗示滞后状态对当前状态的权重指数衰减，长期梯度流在学习过程中快速消失。

Hochreiter和Schmidhuber（1997）提出RNN的特殊形式长短期记忆（LSTM）模型，通过控制信息从 h t − 1 h_{t-1} ht−1流向 h t h_t ht的门函数系列（为记法简便省略i依赖）容纳短期与长期依赖混合：

h t = o t ⊙ tanh ⁡ ( c t ) , c t = f t ⊙ c t − 1 + i t ⊙ c ~ t , h_t = o_t \odot \tanh(c_t), \quad c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t, ht=ot⊙tanh(ct),ct=ft⊙ct−1+it⊙c~t,

其中 ⊙ \odot ⊙表示元素乘， c t c_t ct为细胞状态， i t , o t i_t, o_t it,ot, f t f_t ft为门------自身是 z t z_t zt与 h t − 1 h_{t-1} ht−1的sigmoid函数：

a t = σ ( W a z t + U a h t − 1 + b a ) , a_t = \sigma(W_a z_t + U_a h_{t-1} + b_a), at=σ(Wazt+Uaht−1+ba),

其中 a a a可为输入门 i i i、输出门 o o o或遗忘门 f f f， W a , U a W_a, U_a Wa,Ua, b a b_a ba为参数。

细胞状态如传送带运作，代表模型的"记忆"单元。 c t − 1 c_{t-1} ct−1的过去值通过 f t f_t ft调整加性贡献至 c t c_t ct，此机制使网络能记忆长期信息。同时 f t f_t ft控制遗忘多少过去信息，故称遗忘门。来自 h t − 1 h_{t-1} ht−1与 z t z_t zt的新信息通过 c ~ t \tilde{c}_t c~t注入：

c ~ t = tanh ⁡ ( W c z t + U c h t − 1 + b c ) , \tilde{c}t = \tanh(W_c z_t + U_c h{t-1} + b_c), c~t=tanh(Wczt+Ucht−1+bc),

其被输入门 i t i_t it控制记忆内容。最终， o t o_t ot决定传递至下隐藏状态 h t h_t ht的信息，故称输出门。

尽管对时间序列建模有用，LSTM及相关方法（如Cho等（2014）的门控循环单元）在实证金融文献中应用较少。前文讨论Bali等（2020）预测公司债收益的显著例外。（Guijarro-Ordonez等，2022）用RNN架构预测日股票收益。另一例是Cong等（2020），他们在月股票收益预测中比较简单前馈网络与LSTM等循环神经网络，发现LSTM设定的预测优于前馈对应物，但其设定描述有限且分析更符合计算机科学文献规范。事实上，计算机科学文献有相当体量使用各类神经网络预测股票收益（如Sezer等，2020）。该文献的标准实证分析旨在通过小规模示例实验展示基本概念验证，倾向于高频（日或日内，而非可能更具经济意义的月或年）或分析单只或少数资产（而非更具代表性的资产横截面）。¹⁰ 这与金融经济学文献中更广泛的实证分析形成对比------后者通常分析大量资产的月度或年度数据。

¹⁰ 例如Rather等（2015）、Singh和Srivastava（2017）、Chong等（2017）、Bao等（2017）。

3.10 "另类"数据的收益预测模型

另类（或俗称"alt"）数据已成资产管理行业热门话题，近期研究在开发某些alt数据的机器学习模型方面取得进展。本节讨论两例------文本数据与图像数据，及为其定制的监督机器学习模型。

3.10.1 文本分析

文本分析是金融与经济学研究中最激动人心且发展最快的前沿之一。早期文献从研究者"细读"（如Cowles，1933）演变为基于词典的情感评分方法（如Tetlock，2007），由Das等（2014）、Gentzkow等（2019）及Loughran和McDonald（2020）综述。本节聚焦应用于金融预测的文本监督学习。

Jegadeesh和Wu（2013）、Ke等（2019）及Garcia等（2022）是使用词频或"词袋"（BoW）文本表示定制收益预测监督学习模型的示例。Ke等（2019）描述新闻文章关于股票及其后续收益的联合概率模型，文章由单一潜在"情感"参数索引------决定文章对股票利好或利空的倾向，该参数同时预测股票未来收益方向。从新闻文章及相关收益的训练样本中，Ke等（2019）估计最具情感倾向（即最具收益预测力）的术语集及其关联情感值（即预测系数），实质是构建针对特定监督学习任务定制情感词典的数据驱动方法。

其方法称为"通过筛选与主题建模的情感提取"（SESTM），含三个核心组件：首步通过预测相关性筛选从超大词汇表隔离最相关术语；次步用监督主题模型分配术语特定情感权重；第三步用估计主题模型通过惩罚最大似然分配文章级情感分数。

SESTM计算简便廉价，模型自身解析易处理，估计量归结为两个核心方程，强调简洁性与可解释性，故为"白箱"易检视解释，不同于围绕强大但不透明神经网络嵌入设定的最新NLP模型。图3.8以词云形式报告最具收益预测力的标记系数估计，按正负系数分割词云，各标记大小与其估计预测系数幅度成比例。

图8：情感词

注 ：该图报告情感集 S S S中的词列表，词字体大小与其在所有17个训练样本的平均情感色调成比例。

Ke等（2019）设计系列交易策略展示SESTM的强大收益预测力。在直接比较中，SESTM显著优于领先商业情感评分供应商RavenPack（被大型资产管理公司使用）及Loughran和McDonald（2011）等词典方法。

多篇论文将监督学习模型应用于BoW文本数据预测其他金融结果。Manela和Moreira（2017）用支持向量回归预测市场波动率。Davis等（2020）用10-K风险因子披露理解公司在COVID-19疫情中的差异收益响应，利用Taddy（2013）的多项逆回归方法。Kelly等（2018）引入称为障碍分布多项回归（HDMR）的方法改进计数模型设定，用之构建衡量金融中介部门健康状况的文本指数。

这些分析分两步进行：第一步决定文本数据的数值表示；第二步将该表示作为计量经济模型数据描述经济现象（如上述文献中的资产收益、波动率与宏观经济基本面）。

上述金融文本表示存在局限：首先均始于BoW表示------过度简化且仅访问可通过术语使用频率传达的文本信息，牺牲几乎所有通过词序或术语间上下文关系传达的信息；其次，BoW表示的超高维度导致统计低效------第二步计量模型须包含众多参数处理所有这些术语，尽管多数术语传达可忽略信息。LDA等相关性筛选等降维有益，因其缓解BoW的低效，但它们派生自BoW故无法避免依赖词频的首步信息损失；第三，降维表示是语料库特定的------如Bybee等（2020）构建主题模型时，主题仅从《华尔街日报》估计，尽管许多主题是通用语言结构，或可通过使用样本外额外文本更好推断。

Jiang等（2023）通过构建源自所谓"大语言模型"（LLMs）的精炼新闻文本表示推动文献前进，随后用这些表示改进预期股票收益模型。LLMs在跨越多源多主题的大文本数据集训练，由执行在真正大数据（包括完整书籍与互联网巨大部分的海量文本示例）上估计具有天文参数化通用语言模型这一艰巨任务的专门研究团队训练。但每个LLM的估计壮举执行一次后，估计模型便可供非专业研究者在下游任务部署分发。

换言之，LLM将上述程序的第一步委托给全球最能执行该步骤的少数专家。第二步计量经济模型可围绕LLM输出构建。如LDA（甚至BoW），基础模型的输出是文档的数值向量表示（或"嵌入"），非专业研究者通过将感兴趣文档输入软件（许多情况下开源）获得该输出。LLMs在第一步的主要益处是提供比上述文献更复杂训练良好的文本表示，该益处来自重型非线性模型参数化的表现力及跨多领域、贯穿人类历史、多语言的大量语言示例训练。LLMs的可迁移性使这一空前规模的知识可用于金融研究。

Jiang等（2023）分析通过多个LLMs（包括Devlin等（2018）的双向编码器表示转换器（BERT）、Radford等（2019）的生成预训练转换器（GPT）及Zhang等（2022）的开放预训练转换器（OPT））处理新闻文本的收益预测，发现预训练LLM嵌入的预测在样本外交易策略表现上优于主流基于文本的机器学习收益预测，且LLMs的优越表现源于其能更成功捕捉文档中的上下文含义。

3.10.2 图像分析

现代机器学习的许多进展围绕图像分析与计算机视觉任务，图像相关任务的大幅提升源自卷积神经网络（CNN）模型的发展。Jiang等（2022）将CNN图像分析技术引入收益预测问题。

大量金融文献研究过去价格模式如何预测未来收益。这些分析的哲学视角多为假设检验------研究者基于价格趋势（如用过去十二个月平均收益回归一月后收益）构建收益预测模型作为弱式有效市场原假设的检验。但文献中难以看到具体的备择假设。换言之，文献研究的基于价格的收益预测变量多为临时性且在学术研究幕后通过人类密集型统计学习发现。Jiang等（2022）从机器学习奠基的不同哲学视角重新思考基于价格的收益可预测性。鉴于近期在理解人类行为如何影响价格模式（如Barberis和Thaler，2003；Barberis，2018）的进展，有理由预期价格包含可能难以发展具体可检验假设的微妙复杂模式。Jiang等（2022）设计系统的机器学习方法从价格数据中提取潜在的收益预测模式，而非检验特定临时假设。

此类探索的挑战在于平衡能检测潜在微妙模式的灵活模型与保持模型可处理性和可解释性的愿望。为此，Jiang等（2022）将历史价格表示为图像，用成熟的CNN图像分析机制搜索预测模式。其图像包含叠加多日收盘价移动平均线与日交易量柱状图的日开盘、最高、最低、收盘价（后称"OHLC"图）（见图3.9雅虎财经相关示例）。

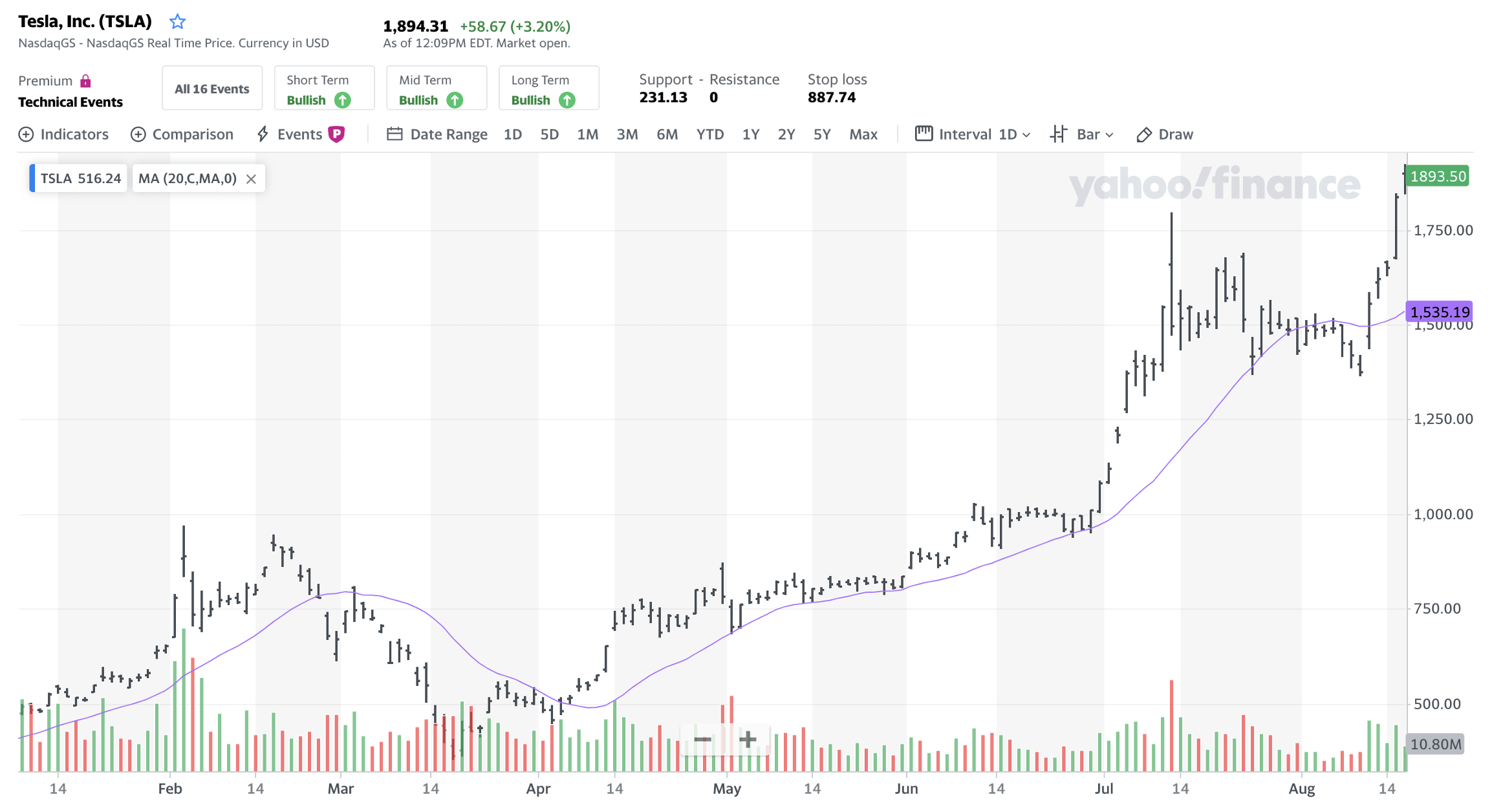
图9：特斯拉OHLC图（雅虎财经）

注：特斯拉股票的OHLC图含20日移动平均价格线与日成交量柱。2020年1月1日至8月18日的日数据。

CNN设计为自动从图像提取对监督标签（Jiang等（2022）中为未来实现收益）具预测力的特征。原始数据由像素值数组组成，CNN通常有少数核心构建块将像素数据转换为预测特征。构建块按应用特定伸缩配置堆叠，空间平滑图像内容以降噪并突出形状轮廓以最大化图像与标签的相关性。构建块的参数作为模型估计过程的一部分学习。

每个构建块含三个操作：卷积、激活与池化。"卷积"是时间序列核平滑的空间类似物，扫描图像并对图像矩阵中每个元素生成其紧邻区域的图像内容摘要。卷积通过一组习得的"滤波器"（即平均邻近矩阵元素的低维核权重矩阵）运作。

构建块的第二操作"激活"是逐元素应用于卷积滤波器输出的非线性变换。例如"Leaky ReLU"激活使用凸分段线性函数，可视为锐化特定卷积滤波器输出的分辨率。

构建块的最终操作是"最大池化"，该操作使用扫描输入矩阵并返回每位置进入滤波器的元素最大值的小滤波器。最大池化同时作为降维与去噪工具。

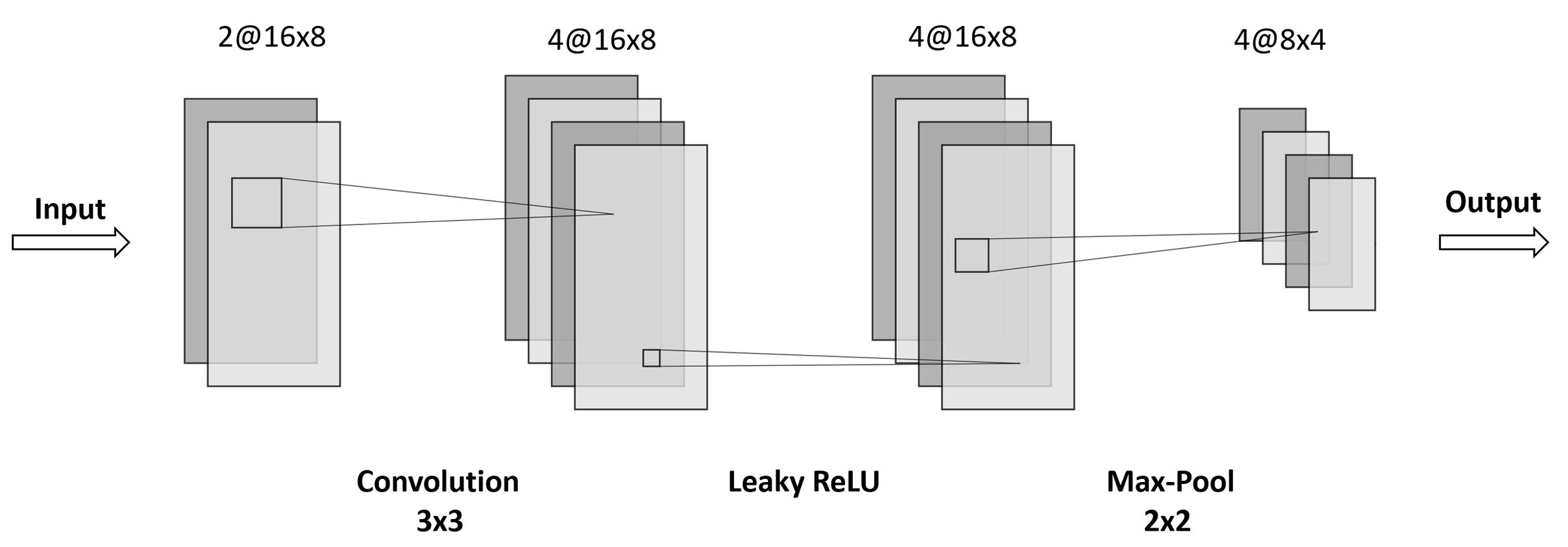
图10：构建块示意图

注 ：CNN模型的构建块包含带3×3滤波器的卷积层、leaky ReLU层及2×2最大池化层。此玩具例中，输入为2通道16×8大小，应用4个滤波器使输出深度翻倍至4通道。最大池化层将输入的前两维（高与宽）缩半并保持深度不变。Leaky ReLU保持前输入相同尺寸。一般地，尺寸 h × w × d h \times w \times d h×w×d的输入产生尺寸 h / 2 × w / 2 × 2 d h/2 \times w/2 \times 2d h/2×w/2×2d的输出。例外是每个CNN模型的首个构建块以灰度图像为输入：输入深度为1，CNN滤波器数为32，使输出深度增至32。

图3.10展示卷积、激活与最大池化如何组合形成CNN模型的基本构建块。通过堆叠多个此类块，网络首先生成图像小部分的表示，随后逐步组装为更大区域的表示。末个构建块的输出展平为向量，每元素视为最终预测步骤的标准全连接前馈层中的特征。¹¹

¹¹ Goodfellow等（2016）第9章提供CNN的更一般介绍。

Jiang等（2022）训练面板CNN模型预测未来股票收益方向，使用1993至2019年美股的日数据。基于CNN正价格变动概率的周再平衡多空十分位差策略的等权年化夏普比为7.2，市值加权为1.7，大幅显著超越知名价格趋势策略------各类动量与反转。他们表明图像表示是模型成功的关键驱动，因其他时间序列神经网络设定难以匹配图像CNN的表现。Jiang等（2022）指出其策略或可部分近似为用更简单信号替代CNN预测------具体而言，最新收盘价接近近几日高低区间底部的股票往往在随后周升值。该模式此前未在文献中研究，由CNN从图像数据检测且在时间、市值段与国家间稳定。

Glaeser等（2018）用住宅房地产图像研究房地产市场，用预训练CNN模型（He等（2016）的Resnet-101）将图像转换为每房产的特征向量，随后用主成分进一步浓缩，最终将成分加入标准特征价格模型。Glaeser等（2018）发现源自图像的房产数据改进特征价格模型的样本外拟合。Aubry等（2022）通过使用艺术品图像伴随非视觉特征的神经网络预测艺术品拍卖价格，用其模型记录艺术品市场的若干信息低效。Obaid和Pukthuanthong（2022）应用CNN分类《华尔街日报》照片构建日投资者情绪指数，预测市场收益反转与交易量，该关联在套利限制更严的股票及高风险期最强，还发现照片传达与新闻文本不同的信息。¹²

¹² 相关地，Deng等（2022）提出理论模型合理化10-K报告图形内容如何影响股票收益。