【图像翻转+图像的仿射变换】——图像预处理（OpenCV）

[1 图像翻转（图像镜像旋转）](#1 图像翻转（图像镜像旋转）)

[2 图像仿射变换](#2 图像仿射变换)

[2.1 图像旋转](#2.1 图像旋转)

[2.2 图像平移](#2.2 图像平移)

[2.3 图像缩放](#2.3 图像缩放)

[2.4 图像剪切](#2.4 图像剪切)

1 图像翻转（图像镜像旋转）

在OpenCV中，图像翻转是以图像中心点为原点进行镜像翻转的。

API：

复制代码

cv.filp(img,flipcode)

参数：

img:要翻转的图像
flipcode=0：垂直翻转，沿x轴翻转
flipcode>0：水平翻转，沿y轴翻转
flipcode<0：水平垂直翻转

案例：

python 复制代码

import cv2 as cv
# 读取图像
cat = cv.imread("./images/cat1.png")
cat_r = cv.resize(cat,(480,480))
# 图像翻转：cv2.flip(img,翻转类型标志0、-1、1),原点在图像的中心位置
# 垂直翻转：filpcode=0,沿x轴翻转，上下翻转
flip0 = cv.flip(cat_r,0)
# 水平翻转：flipcode=1,沿y轴翻转，左右翻转
flip1 = cv.flip(cat_r,1)
# 水平+垂直翻转：flipcode=-1,沿x和y都翻转
flip_1 = cv.flip(cat_r,-1)
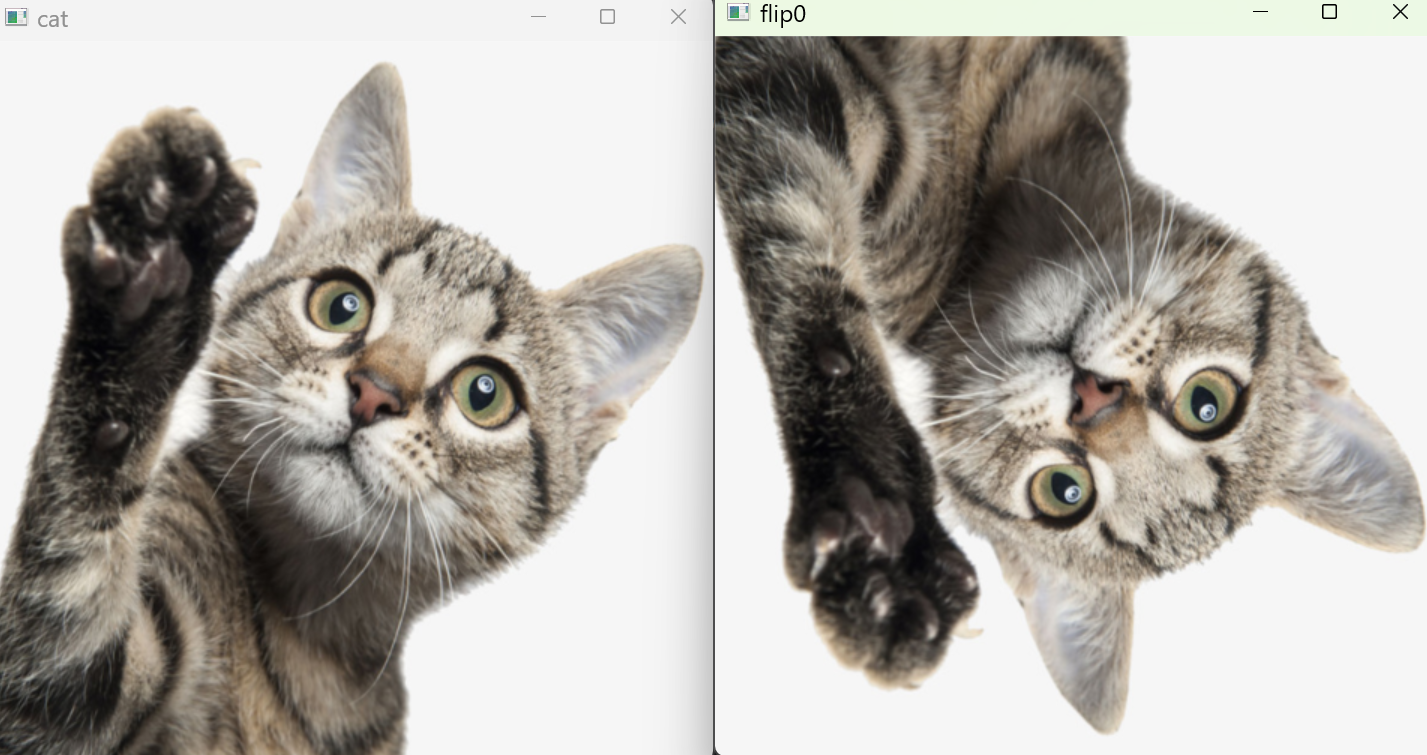
cv.imshow("cat",cat_r)
cv.imshow("flip0",flip0)
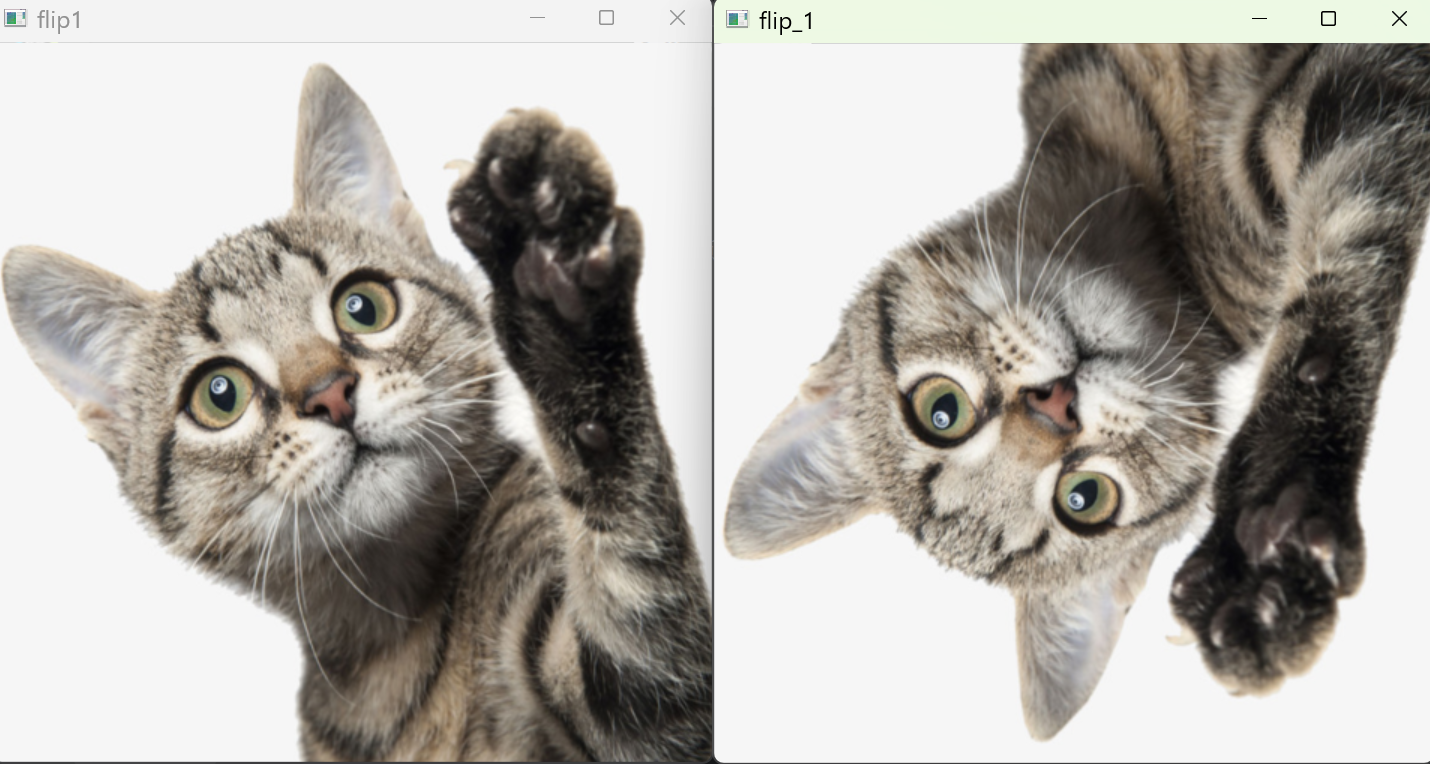
cv.imshow("flip1",flip1)
cv.imshow("flip_1",flip_1)
cv.waitKey(0)
cv.destroyAllWindows()

输出：

2 图像仿射变换

仿射变换是一种线性变换，保持了点与点之间相对距离不变。

基本性质：保持直线、保持平行、比例不变性、不保持角度和长度。

基本原理：

二维空间中，图像点坐标为(x,y)，仿射变换的目标是将这些点映射到新的位置 (x', y')。
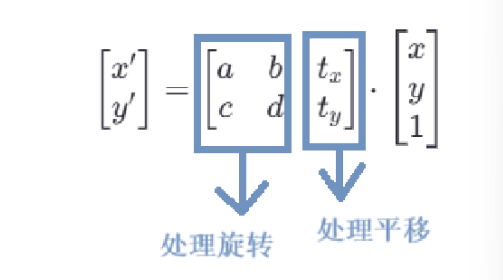
为了实现这种映射，通常会使用一个矩阵乘法的形式：

（类似于y=kx+b）

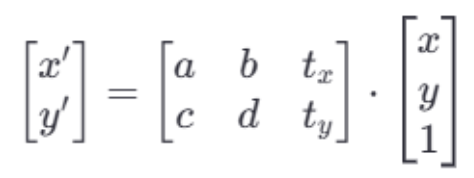
a，b，c，d 是线性变换部分的系数，控制旋转、缩放和剪切。
是平移部分的系数，控制图像在平面上的移动。
输入点的坐标被扩展为齐次坐标形式[x,y,1]，以便能够同时处理线性变换和平移

API：

复制代码

cv2.warpAffine(img,M,dsize)

参数：

M ：2x3的变换矩阵，类型为np.float32。
dsize ：输出图像的尺寸，形式为(width,height)。

2.1 图像旋转

图像绕着某个点或轴旋转一定角度

API：

复制代码

cv2.getRotationMatrix2D(center,angle,scale)

center ：旋转中心点的坐标，格式为(x,y)。
angle：旋转角度，单位为度，正值表示逆时针旋转负值表示顺时针旋转。
scale：缩放比例，若设为1，则不缩放。
返回值 ：M，2x3的旋转矩阵。

案例：

python 复制代码

import cv2 as cv
# 读取图像
cat = cv.imread("./images/cat1.png")
# 获取图像宽高
h,w,_ = cat.shape
# h,w = cat.shape[:2]
# 设置旋转中心
center = (w//2,h//2)
# 旋转角度
angle = 45
# 缩放比例
scale = 0.6
# 获取旋转矩阵
M = cv.getRotationMatrix2D(center,angle,scale)
# 使用仿射变换函数进行仿射变换
img = cv.warpAffine(cat,M,(w,h))
# 显示图像
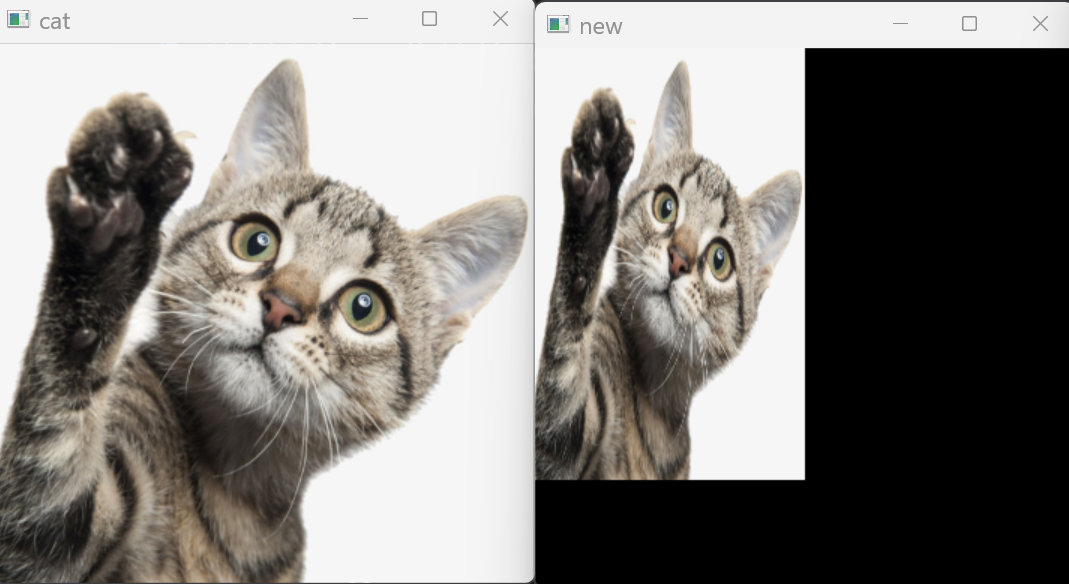
cv.imshow("cat",cat)
cv.imshow("new",img)
cv.waitKey(0)
cv.destroyAllWindows()

输出：

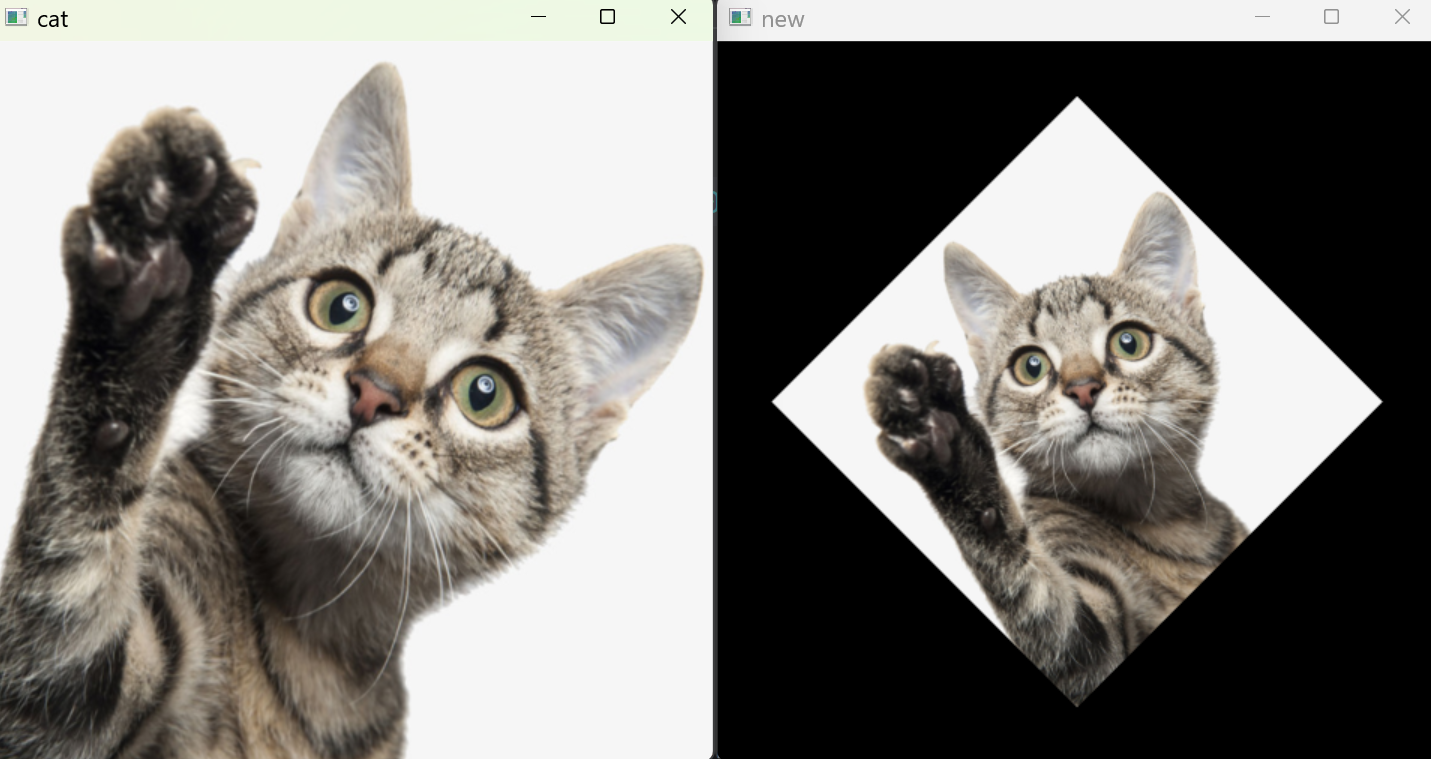
2.2 图像平移

仅改变物体的位置，不改变其形状和大小

假设我们有一个点 P(x,y)，希望将其沿x轴方向平移个单位，沿y轴方向平移个单位到新的位置P′(x′,y′)，那么平移公式如下：

在矩阵形式下，该变换可以表示为：

这里的和分别代表在x轴和y轴上的平移量。

案例：

python 复制代码

# 读取图像->设置参数->获取旋转矩阵->再用仿射变换函数进行旋转->显示图像
# 读取图像->设置参数（平移量tx,ty）->获取平移矩阵np.float32->仿射变换函数进行平移->显示图像
import cv2 as cv
import numpy as np
# 读取图像
cat = cv.imread("./images/cat1.png")
cat = cv.resize(cat,(480,480))
# 定义相关参数：平移量
tx,ty = 80,50
# 获取平移矩阵
M = np.float32([[1,0,tx],[0,1,ty]])
# 使用仿射变换函数进行平移
img = cv.warpAffine(cat,M,(cat.shape[1],cat.shape[0]))
# 显示图像
cv.imshow("cat",cat)
cv.imshow("new",img)
cv.waitKey(0)
cv.destroyAllWindows()

输出：

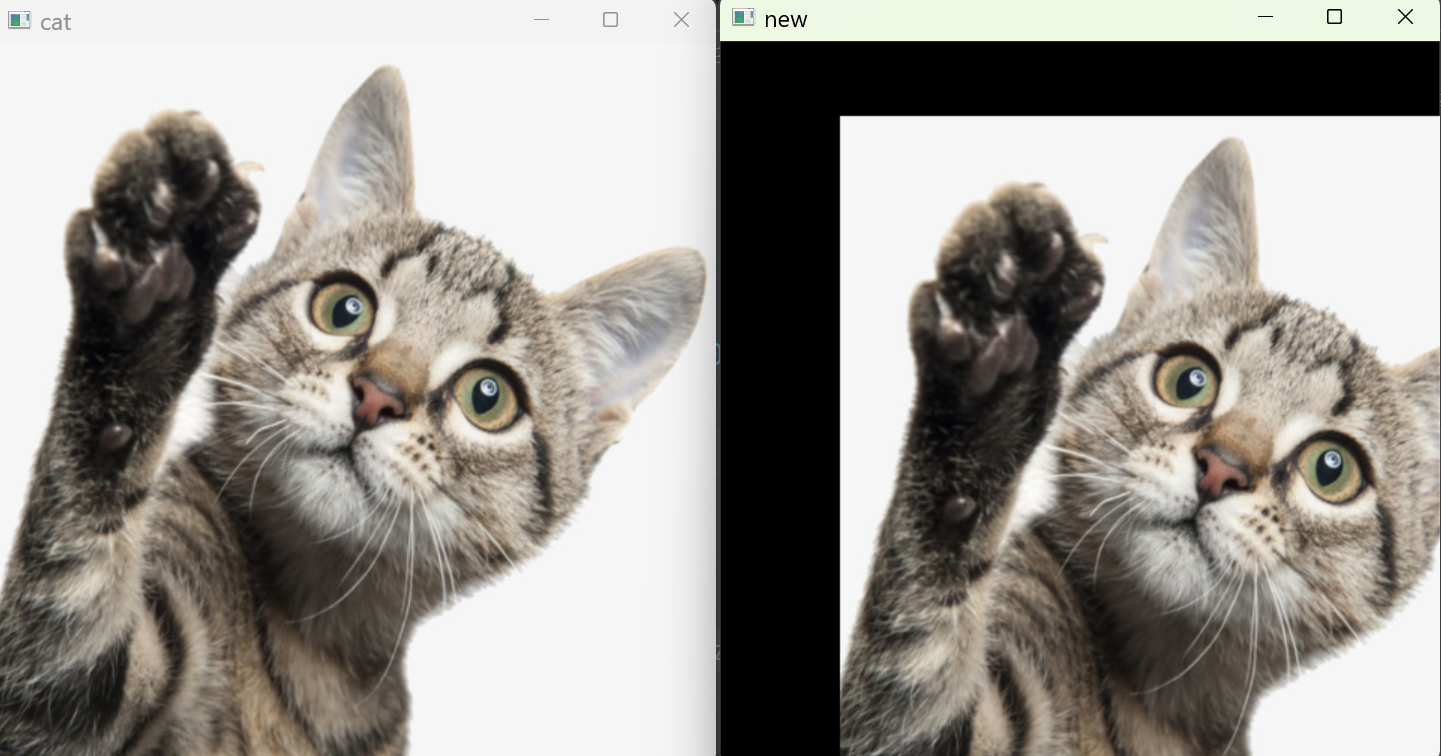
2.3 图像缩放

改变物体的大小

假设要把图像的宽高分别缩放为0.5和0.8，那么对应的缩放因子=0.5，=0.8。
点P(x,y)对应到新的位置P'(x',y')，缩放公式为：

在矩阵形式下，该变换可以表示为：

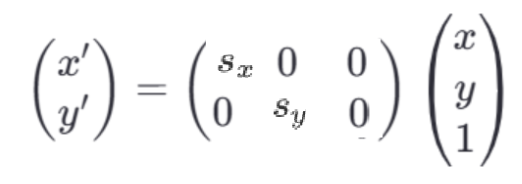
相较于图像旋转中只能等比例的缩放，图像缩放更加灵活，可以在指定方向上进行缩放。

和分别表示在x轴和y轴方向上的缩放因子。

案例：

python 复制代码

import cv2 as cv
import numpy as np
# 读取图像
cat = cv.imread("./images/cat1.png")
cat_r = cv.resize(cat,(360,360))
# 获取宽高
h,w,_ = cat_r.shape
# 定义缩放因子 sx*x sy*y
sx,sy = 0.5,0.8
# 变换后的图像宽高
w1,h1 = int(w*sx),int(h*sy)
# 获取缩放矩阵
M = np.float32([[sx,0,0],[0,sy,0]])
# 使用仿射变换函数进行缩放
img = cv.warpAffine(cat_r,M,(w,h))  # 输出图像尺寸是原图大小
img_2 = cv.warpAffine(cat_r,M,(w1,h1)) # 输出图像尺寸是缩放后大小
# 显示图像
cv.imshow("cat",cat_r)
cv.imshow("new",img)
cv.imshow("new_2",img_2)
cv.waitKey(0)
cv.destroyAllWindows()

输出：

2.4 图像剪切

使物体发生倾斜变形。剪切操作可以改变图形的形状，以便其在某个方向上倾斜，它将对象的形状改变为斜边平行四边形，而不改变其面积。

想象我们手上有一张矩形纸片，如果你固定纸片的一边，并沿着另一边施加一个平行于该边的力，这张纸片就会变形为一个平行四边形。这就是剪切变换的一个直观解释。
对于二维空间中的点P(x,y)，对他进行剪切变换：

沿x轴剪切 ：

沿y轴剪切 ：
当需要同时沿两个方向进行剪切时，
在矩阵形式下，该变换可以表示为：

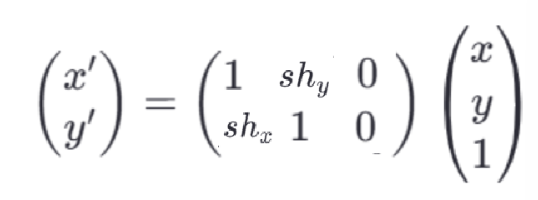
来一个图理解一下：

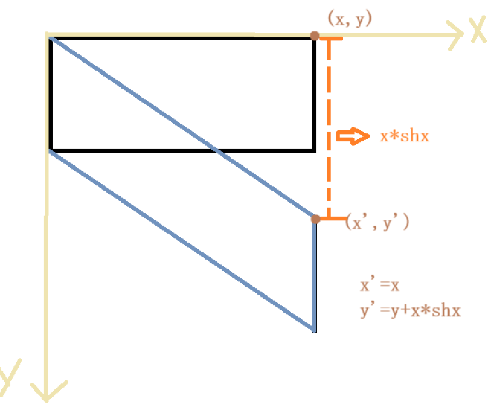
案例：

python 复制代码

import cv2 as cv
import numpy as np
# 读取图像
cat = cv.imread("./images/cat1.png")
cat_r = cv.resize(cat,(300,300))
# 定义参数，剪切因子
shx,shy = 0.2,0.2
# 定义在x轴方向的剪切矩阵
M_x = np.float32([[1, shy, 0], [0, 1, 0]])
# 定义在y轴方向的剪切矩阵
M_y = np.float32([[1, 0, 0], [shx, 1, 0]])
# 定义在x轴和y轴方向的剪切矩阵
M_xy = np.float32([[1, shy, 0], [shx, 1, 0]])
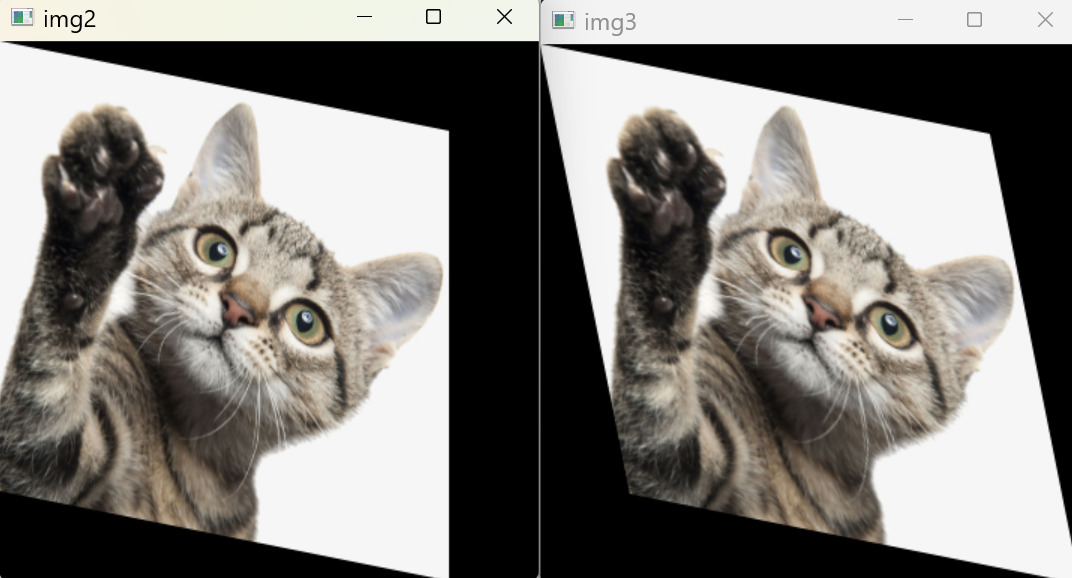
# 运用仿射变换函数对图像进行剪切
img_x = cv.warpAffine(cat_r, M_x, (360, 360))
img_y = cv.warpAffine(cat_r, M_y, (360, 360))
img_xy = cv.warpAffine(cat_r, M_xy, (360, 360))
# 显示图像
cv.imshow("cat",cat_r)
cv.imshow("img", img_x)
cv.imshow("img2", img_y)
cv.imshow("img3", img_xy)
cv.waitKey(0)
cv.destroyAllWindows()

输出：