算法第三十七天：动态规划part05（第九章）

一.完全背包理论基础-二维DP数组

复制代码

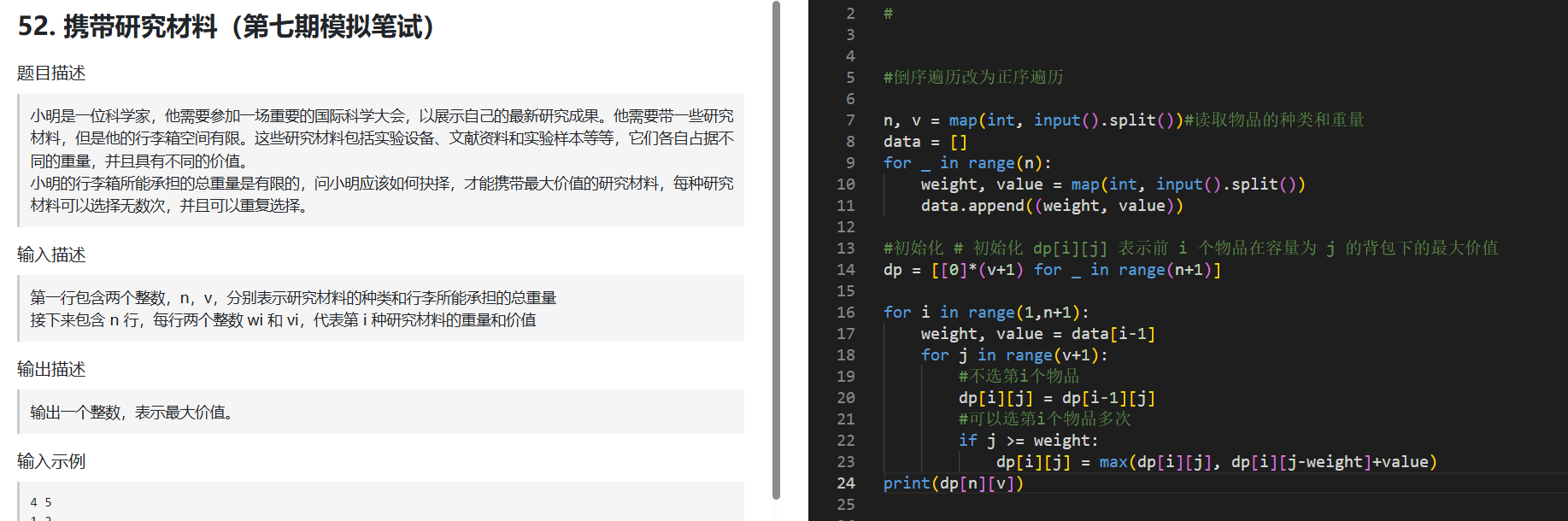
#每个背包可以使用无数次

#倒序遍历改为正序遍历

n, v = map(int, input().split())#读取物品的种类和重量
data = []
for _ in range(n):
    weight, value = map(int, input().split())
    data.append((weight, value))

#初始化 # 初始化 dp[i][j] 表示前 i 个物品在容量为 j 的背包下的最大价值
dp = [[0]*(v+1) for _ in range(n+1)]

for i in range(1,n+1):
    weight, value = data[i-1]
    for j in range(v+1):
        #不选第i个物品
        dp[i][j] = dp[i-1][j]
        #可以选第i个物品多次
        if j >= weight:
            dp[i][j] = max(dp[i][j], dp[i][j-weight]+value)
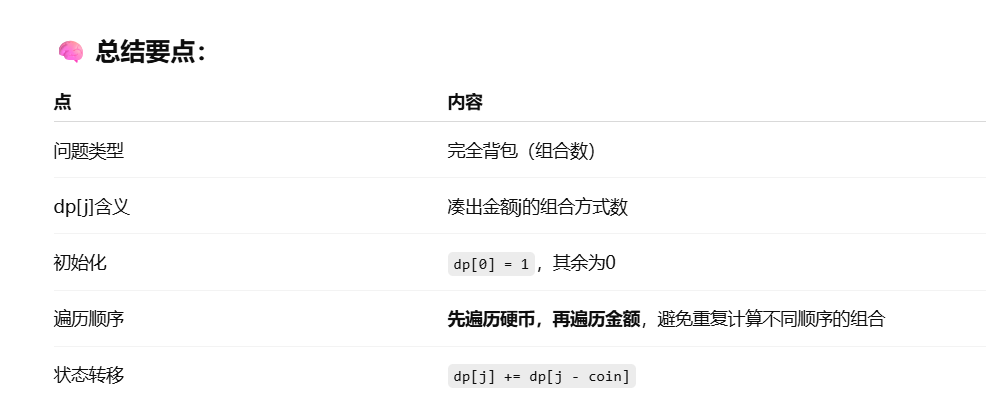
print(dp[n][v])

2.零钱兑换Ⅱ：组合数：先遍历物品后遍历背包

518. 零钱兑换 II - 力扣（LeetCode）

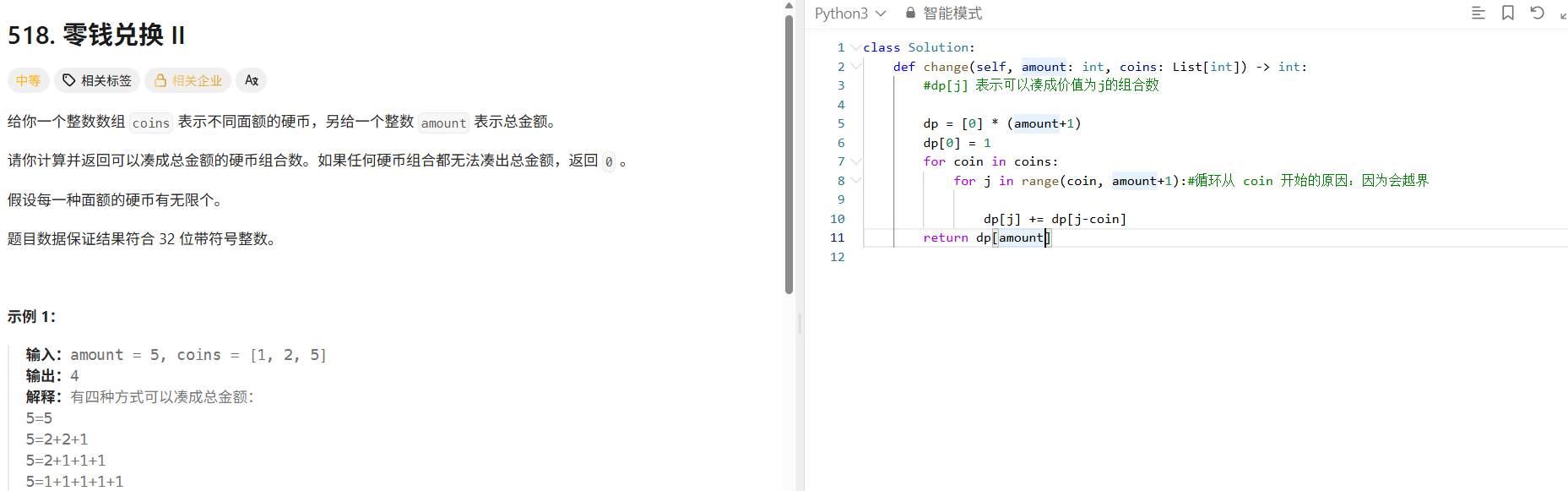
思路：

复制代码

class Solution:
    def change(self, amount: int, coins: List[int]) -> int:
        #dp[j] 表示可以凑成价值为j的组合数

        dp = [0] * (amount+1)
        dp[0] = 1
        for coin in coins:
            for j in range(coin, amount+1):#循环从 coin 开始的原因：因为会越界

                dp[j] += dp[j-coin]
        return dp[amount]

3.组合总合Ⅳ ：排列：先遍历背包再遍历物品

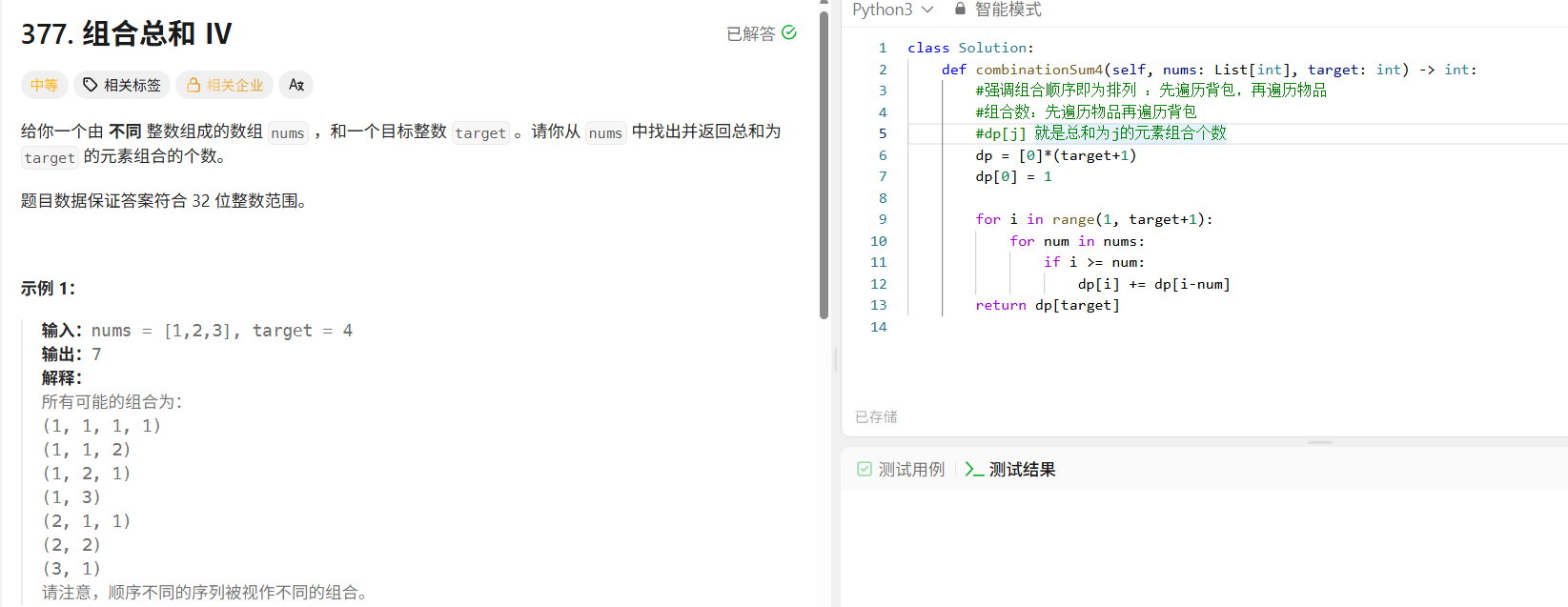
思路：

✅ 思路总结：

📌 1. 本质是一个完全背包问题的变形：

数组元素可以重复使用；
关键在于：组合顺序不同视作不同的结果 ，即 [1,2] 和 [2,1] 被认为是两种不同的组合；
所以我们要计算的是排列数（而非组合数）。

2. 状态定义：

定义 dp[i] 表示：凑出目标和为 i 的组合（排列）数。

📌 3. 初始化：

dp = [0] * (target + 1) dp[0] = 1 # 凑出 0 有 1 种方式：什么都不选

为什么 dp[0]=1？表示凑成 0 元，有 1 种方式（空序列），这是构建递推关系的基础。

📌 4. 状态转移方程（排列 vs 组合的核心区别）：

复制代码

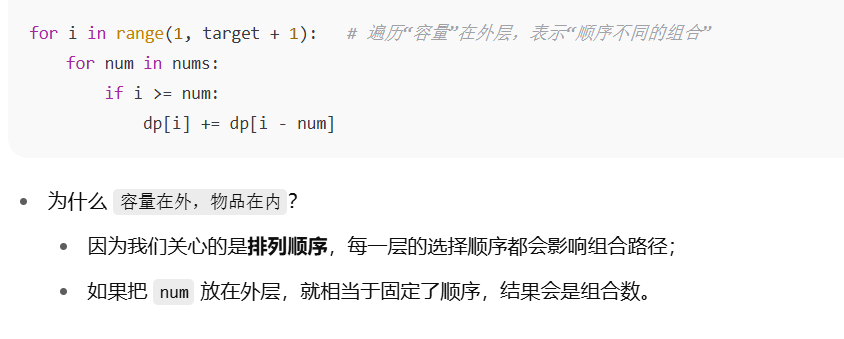
class Solution:
    def combinationSum4(self, nums: List[int], target: int) -> int:
        #强调组合顺序即为排列 ：先遍历背包，再遍历物品
        #组合数：先遍历物品再遍历背包
        #dp[j] 就是总和为j的元素组合个数
        dp = [0]*(target+1)
        dp[0] = 1

        for i in range(1, target+1):
            for num in nums:
                if i >= num:
                    dp[i] += dp[i-num]
        return dp[target]

4.爬楼梯：不难套公式，属于排列问题，先背包后物品

复制代码

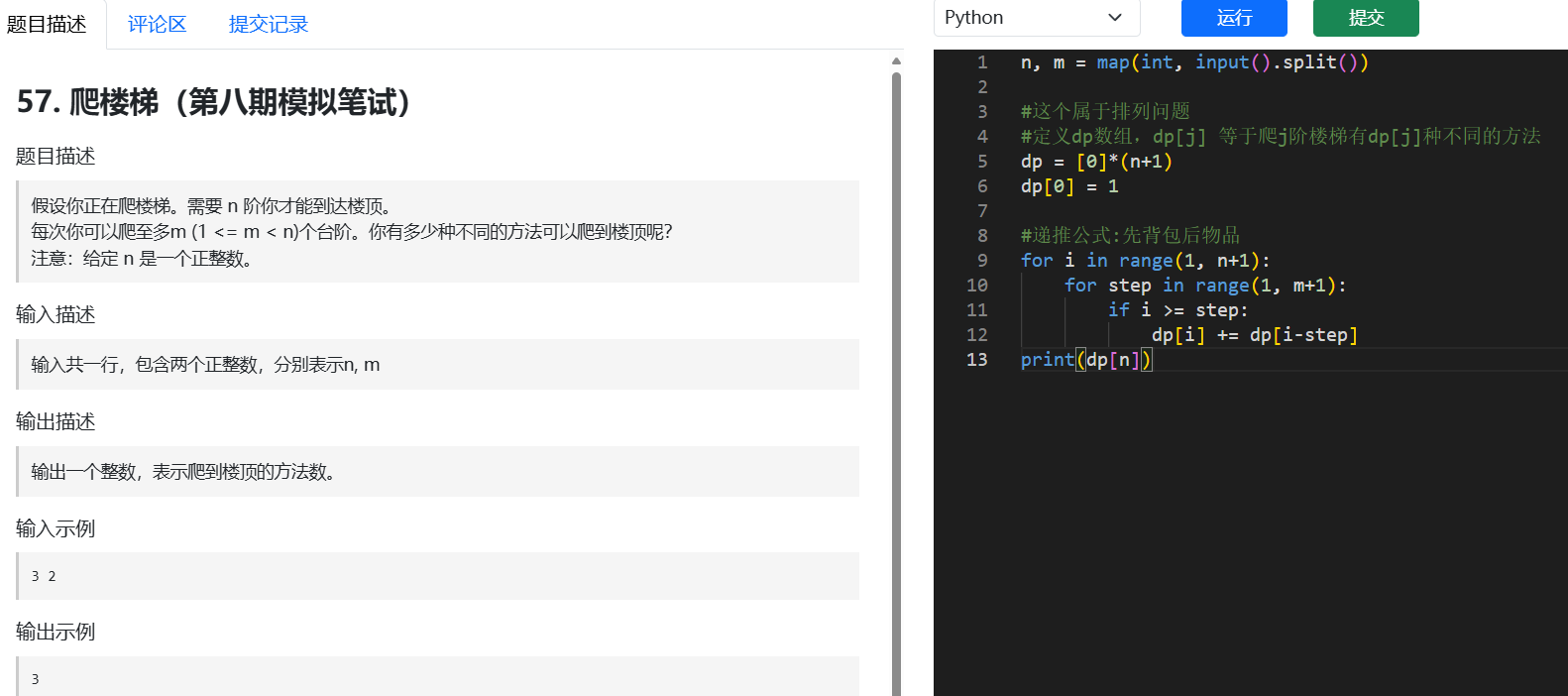
n, m = map(int, input().split())

#这个属于排列问题
#定义dp数组，dp[j] 等于爬j阶楼梯有dp[j]种不同的方法
dp = [0]*(n+1)
dp[0] = 1

#递推公式:先背包后物品
for i in range(1, n+1):
    for step in range(1, m+1):
        if i >= step:
            dp[i] += dp[i-step]
print(dp[n])

今天就到这里结束啦！明天继续！