论文阅读--《Besting the Black-Box: Barrier Zones for Adversarial Example Defense》

好的，这是《Besting the Black-Box: Barrier Zones for Adversarial Example Defense》论文的中文翻译：

$文件名称$ : Besting_the_Black-Box_Barrier_Zones_for_Adversarial_Example_Defense.pdf
$文件内容开始$

===== 第 1 页 =====

收稿日期：2021年10月13日，录用日期：2021年12月17日，发布日期：2021年12月27日，当前版本日期：2022年1月6日。

数字对象标识符 10.1109/ACCESS.2021.3138966

击败黑盒：用于对抗样本防御的屏障区

KALEEL MAHMOOD1^11, PHUONG HA NGUYEN2^22, LAM M. NGUYEN3^33, THANH NGUYEN4^44, AND MARTEN VAN DIJK5^55 (IEEE 高级会员)

1^11 康涅狄格大学电气与计算机工程系，美国康涅狄格州斯托尔斯市，邮编 06269
2^22 eBay 公司，美国加利福尼亚州圣何塞市，邮编 95125
3^33 IBM 研究院，托马斯·J·沃森研究中心，美国纽约州约克敦海茨市，邮编 10562
4^44 亚马逊公司，美国华盛顿州西雅图市，邮编 98109
5^55 荷兰阿姆斯特丹国家数学与计算机科学研究院 (CWI)，邮编 1098

通讯作者：Kaleel Mahmood (kaleel.mahmood@uconn.edu)

摘要对抗性机器学习防御主要集中于缓解静态的白盒攻击。然而，此类防御在自适应的黑盒对手下是否鲁棒仍然是一个悬而未决的问题。在本文中，我们特别关注黑盒威胁模型，并做出以下贡献：首先，我们开发了一种增强的自适应黑盒攻击，实验表明其比 Papernot 等人提出的原始自适应黑盒攻击有效 ≥30%\geq 30\%≥30%。作为我们的第二个贡献，我们使用我们的新攻击测试了 10 种近期防御方法，并提出了我们自己的黑盒防御（屏障区）。我们表明，基于屏障区的防御在安全性上相比最先进的防御方法提供了显著的改进。对于我们研究的数据集（CIFAR-10 和 Fashion-MNIST），这种改进包括对黑盒边界攻击、迁移攻击以及我们新的自适应黑盒攻击具有超过 85%85\%85% 的鲁棒精度。为完备起见，我们通过在两个数据集（CIFAR-10 和 Fashion-MNIST）上使用三种对抗模型（14 种不同的黑盒攻击）对其他 10 种防御进行广泛实验来验证我们的主张。

索引术语 对抗性机器学习，对抗样本，对抗防御，黑盒攻击，安全性，深度学习。

I 引言

基于卷积神经网络 (CNNs) 的应用有很多，例如图像分类 $1$ , $2$ 、目标检测 $3$ , $4$ 、语义分割 $5$ 和视觉概念发现 $6$ 。然而，众所周知，CNNs 对添加到良性输入图像 xxx 上的微小扰动 η\etaη 高度敏感。如 $7$ , $8$ 所示，通过向原始图像添加视觉上不可察觉的扰动，可以创建对抗样本 x′x'x′，即 x′=x+ηx' = x + \etax′=x+η。这些对抗样本会被 CNN 以高置信度错误分类。因此，使 CNNs 能够抵御此类攻击是一项极其重要的任务。

通常，对抗性机器学习攻击可分为白盒攻击或黑盒攻击。这种分类取决于运行攻击所需关于分类器的信息量。大多数文献集中于白盒攻击 $9$ - $11$ ，其中分类器/防御参数是已知的。同样，大多数防御方法的设计目标也是挫败白盒攻击 $12$ - $24$ 。在本文中，我们关注黑盒攻击，其中分类器参数是隐藏的或假定为秘密的。这种类型的对手

===== 第 2 页 =====

代表了比白盒攻击者更实际的威胁模型 $25$ 。这部分是因为对手无法访问分类器参数，但仍然能够成功创建对抗样本 $25, 26$ 。尽管没有防御参数，黑盒对手仍然可以查询防御，能够访问 X\mathcal{X}X（防御的训练数据集），或者构建一个合成模型来协助创建对抗样本。通过黑盒对抗视角分析防御，我们通过向社区提供新的攻击和防御视角来帮助完善安全图景。具体来说，我们做出以下贡献：

混合黑盒攻击： 我们通过扩展攻击者可用的数据量并改变最终攻击生成方法 ϕ\phiϕ，开发了 Papernot 黑盒攻击 $26$ 的增强版本。这些改变显著提高了攻击成功率，即在 CIFAR-10 和 Fashion-MNIST 上提高了 >30%>30\%>30%。
屏障区防御： 我们基于屏障区（命名为 BARZ）开发了一种新颖的防御。我们表明基于屏障区的防御可以优于本文研究的其他 10 种近期防御方法。这些防御包括 Madry 的对抗训练 $27$ 、随机变换轰炸 $22$ 和集成多样性 $24$ 等。我们结果的概要如图 1 所示，其中我们展示了每种防御在所有 14 种黑盒攻击下的最小鲁棒精度。
δ\deltaδ 指标（次要贡献）： 在对抗性机器学习中，每种防御都涉及两个不同的值需要考虑。这些值是防御的成本（干净精度的下降）和鲁棒性/安全性（在对抗数据上的性能）。我们提出了一种直观的方法，以 δ\deltaδ 指标的形式来帮助衡量鲁棒性和成本之间的权衡。

附录 A 防御方法比较

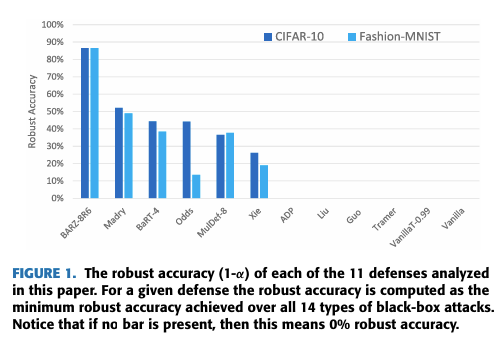
图 1 显示了 BARZ 防御的鲁棒精度（定义为 1−α1-\alpha1−α，其中 α\alphaα 是 14 种黑盒攻击中效果最好的攻击成功率）与其他 10 种近期文献防御的比较。文献将攻击成功率 α\alphaα 定义为被防御错误分类的对抗样本的比例。在此，精确定义术语对抗样本也很重要。简而言之，对抗样本是干净的图像，在未篡改形式下被分类器正确识别，并且攻击者向其添加了对抗性噪声。

因此，仅使用攻击成功率 α\alphaα 并不能给出完整的图景（即图 1 中仅显示了 α\alphaα）。攻击成功率 α\alphaα 仅对应于防御分类器能够正确标记的原始图像的比例。本质上，对于任何给定的防御 ddd，α\alphaα 取决于防御的干净精度 pdp_dpd，而不是最先进的或可达到的最佳干净精度 ppp。这里 ppp 特指在没有任何防御的情况下在干净图像上测量的精度，即干净精度。当存在防御时，我们将该防御的相应干净精度表示为 pdp_dpd。因此，为了完整理解图 1 的故事，我们需要了解防御本身在多大程度上导致普通方案（vanilla scheme）的干净精度从 ppp 降低到 pdp_dpd。

沿着 (a) 鲁棒精度 1−α1-\alpha1−α（攻击者击败防御的能力）和 (b) 防御本身的干净精度 pdp_dpd（无对抗存在时）这两个独立的指标比较防御方法会导致模糊性。不清楚哪个指标被认为更重要，或者哪种组合是"最佳"的。表 1 的第一行描述了非恶意环境（即没有对手），并显示了普通方案（无防御）的精度 ppp（这是我们目前能达到的最佳精度），以及防御的精度 pdp_dpd（如上所述，pd<pp_d < ppd<p）。对于恶意环境，普通方案无法达到任何精度，因为 α=0\alpha=0α=0（见图 2 中的黑盒边界攻击）。这种类型的攻击总是能成功地将一个正确分类的图像转换成一个被普通方案错误分类的对抗样本。在存在对手的情况下，防御正确/准确分类的概率等于表 1 右下角的 pd⋅(1−α)p_d\cdot(1-\alpha)pd⋅(1−α)，因为如果没有对手存在，防御会正确标记一部分 pdp_dpd 的图像，而如果存在对手，这些图像中有一部分 α\alphaα 会被成功攻击。

为避免任何模糊性，我们将两个指标 pdp_dpd 和 1−α1-\alpha1−α 组合成一个单一的"δ\deltaδ-指标"：我们将 δ\deltaδ 定义为从非恶意环境（左上角）中普通方案的干净精度 ppp 到恶意环境中防御的精度 pd⋅(1−α)p_d\cdot(1-\alpha)pd⋅(1−α)（右下角）的精度下降：δ=p−pd⋅(1−α).\delta=p-p_d\cdot(1-\alpha).δ=p−pd⋅(1−α).

当我们分析非恶意环境时，我们只对防御的干净精度感兴趣------因为我们不假设任何攻击。这给出了图 2，其中 y 轴对应于非恶意环境中防御的精度 pdp_dpd，x 轴对应于恶意环境中防御的精度------即，x 轴表示从非恶意环境中普通方案的干净精度到恶意环境中防御精度的下降 δ\deltaδ（抵抗对抗样本的代价）。我们注意到 x 轴和 y 轴可以直接映射到防御干净精度 pdp_dpd 和鲁棒精度 1−α1-\alpha1−α 本身，我们本可以在图中将它们作为 x 轴和 y 轴报告。但这在视觉上无法清晰地表明在恶意环境中哪种组合 (pd,1−α)(p_d, 1-\alpha)(pd,1−α) 是最佳的。

===== 第 3 页 =====

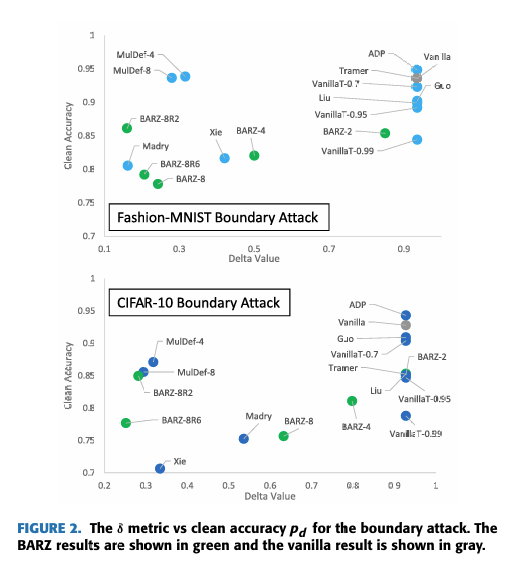
图 2. 边界攻击的 δ 指标与干净精度 pd 的关系图。BARZ 结果以绿色显示，普通方案结果以灰色显示。

我们更倾向于绘制 δ 指标，因为它直接对应于恶意环境中防御分类器的（下降）精度。

在实践中，当评估一个防御时，我们不仅要考虑恶意环境中防御的精度 p−δp - \deltap−δ，还要考虑非恶意环境中防御的精度，即表 1 右上角给出的 pdp_dpd。从纯粹的机器学习角度来看，我们希望防御不会对 ppp 影响"太大"------换句话说，下降 γ=p−pd\gamma = p - p_dγ=p−pd 应该很小，仅限于几个百分点。然而，安全性通常不是免费的，为了最小化 δ\deltaδ，我们可能需要牺牲远超过几个百分点的精度。这意味着我们需要研究最小化 δ\deltaδ 与可接受的 pdp_dpd 之间的权衡。本文提出了这样一项研究，我们的防御 BARZ 旨在最小化 δ\deltaδ，尽管在非恶意环境中可能存在从 ppp 到 pd=p−γp_d = p - \gammapd=p−γ 的显著下降 γ\gammaγ。事实证明，这导致 BARZ 的鲁棒精度优于其他防御，如图 1 和图 2 所示。

B. 大纲

本文其余部分组织如下：在第二节中，我们讨论黑盒对手，解释为什么我们关注某些攻击以及我们新的混合黑盒攻击。在第三节中，我们讨论我们研究的防御方法、它们背后的安全原理以及为什么我们选择这些防御进行分析。在第四节中，我们介绍屏障区防御安全原理背后的数学直觉。我们在第四节讨论屏障区如何在实践中实现，并展示它们的经验证据。在第五节中，我们解释如何简洁地分析防御的效率。我们在第六节给出了所有 11 种防御和 14 种攻击的实验结果。最后，我们在第七节提供总结性评论。

II 攻击

在对抗性机器学习中，白盒和黑盒攻击的通用设置如下 $28$ ：我们假设一个训练好的分类器 fff 正确识别了一个样本 xxx，其类别标签为 yyy。对手的目标是通过某个量 η\etaη 修改 xxx，使得 f(x+η)f (x + \eta)f(x+η) 产生类别标签 y^\hat{y}y^。在非目标攻击的情况下，只要 y^≠y\hat{y} \neq yy^=y，攻击就被认为是成功的。在目标攻击的情况下，只有当 y^≠y\hat{y} \neq yy^=y 且 y^=t\hat{y} = ty^=t（其中 ttt 是攻击者指定的目标类别标签）时，攻击才算成功。对于非目标和目标攻击，通常限制 η\etaη 的幅度 $8$ ，以便人类仍然能够视觉识别图像。

白盒攻击和黑盒攻击的区别在于如何获得 η\etaη。在白盒攻击中，η\etaη 可以通过在分类器上反向传播计算，或者通过将攻击表述为考虑分类器训练参数的优化问题 $7$ , $11$ , $29$ 。白盒对手可以访问训练参数，这些参数可用于计算梯度------本质上，白盒对手可以访问梯度预言机（当被查询时输出梯度信息）。

另一方面，黑盒攻击在生成 η\etaη 时无法访问分类器的参数，必须依赖其他信息。黑盒对手可能有权访问分类器本身，查询时返回一个分数向量或分数最大的标签------我们称之为黑盒预言机。除了黑盒预言机，黑盒对手还可能拥有用于训练分类器的训练数据信息。

从密码学的角度来看，白盒对手严格强于黑盒对手，并且也拥有黑盒预言机的访问权。然而，我们常常忘记白盒对手已知的分类器参数不仅可以用来计算梯度预言机，还可以用来计算黑盒预言机。这是因为我们通常认为梯度信息会导致更强大的攻击，因此我们可能不需要考虑黑盒攻击。一个证明对仅使用梯度预言机的白盒攻击具有鲁棒性的防御，并不总是意味着对黑盒攻击也具有鲁棒性。梯度掩蔽（Gradient masking）使得防御可能对装备齐全的白盒对手产生错误的安全感 $10$ ，因为它只挫败了基于梯度预言机的白盒攻击。这表明，也需要单独测试无梯度攻击，例如黑盒攻击。

在本文中，我们关注利用自适应攻击 $26$ 的黑盒对手。一个自然的问题是，为什么我们关注自适应的黑盒类型攻击？我们这样做有以下原因：

文献中已经对已发表防御的最先进白盒攻击进行了广泛研究 $9$ -- $11$ 。防御论文中对黑盒攻击的关注程度显著较低。通过关注黑盒攻击，我们力求完善安全图景。这个完整的安全图景意味着我们当前分析的防御不仅有其自身出版物中的白盒攻击结果，还有（如本文报告的）自适应黑盒结果。未来的防御可以在进行自身分析时，基于本文开发的安全概念和我们的实验进行构建。这个完善的安全范围将我们引向下一点。

===== 第 4 页 =====

攻击在防御论文中的关注度明显较低。通过关注黑盒攻击，我们力求完善安全图景。这个完整的安全图景意味着我们当前分析的防御不仅有其自身出版物中的白盒攻击结果，还有（如本文报告的）自适应黑盒结果。未来的防御可以在进行自身分析时，基于本文开发的安全概念和我们的实验进行构建。这个完善的安全范围将我们引向下一点。

1. 通过完善（包含黑盒攻击的）安全图景，我们允许读者比较防御结果。这种比较是可行的，因为对每种防御使用了相同的对抗模型、数据集和攻击。这与自适应白盒攻击完全不同，后者可能对每种攻击需要不同的对抗模型和不同的安全假设。例如，在 $9$ 中，为了破解一个检测器防御（The Odds are Odd），在自适应白盒攻击中必须使用自定义目标函数才能达到高攻击成功率。或者，在集成模型防御（ADP $24$ ）上创建自适应白盒攻击则大不相同。唯一的要求是增加基于简单梯度的白盒攻击中使用的迭代次数，使攻击具有适应性和有效性。虽然我们例子中的两种自适应攻击都是白盒攻击，但后者（对 ADP 的自适应白盒攻击）在技术上只需要能够对模型进行反向传播。正如 $30$ 所指出的，在不同对抗模型下比较两种防御的鲁棒性是不合适的。

黑盒攻击变体

纯黑盒攻击 $10, 31, 32, 33$

对手仅被给予一个训练数据集 X0\mathcal{X}_{0}X0 的知识。
基于预言机的黑盒攻击 $26$

攻击者无法访问原始训练数据集，但可以生成与训练数据相似的合成数据集 S0S_{0}S0。对手可以自适应地生成合成数据并查询防御 O\mathcal{O}O 以获得该数据的类别标签。然后使用合成数据集 S0S_{0}S0 来训练合成模型。重要的是要注意，对手无法访问整个原始训练数据集 X0\mathcal{X}_{0}X0。

在本文中，我们提出了这种攻击的一个新版本，我们称之为混合黑盒攻击 。在这种攻击中，对手被给予整个原始训练数据集、生成合成数据的能力以及查询防御以标记数据的权限。在我们的攻击中，对手还有多种不同的对抗生成方法 ϕ\phiϕ 可供选择来创建对抗样本。这样，对手可以训练一个行为更精确地反映防御行为的合成模型。简而言之，攻击者使合成模型适应防御。需要注意的是，此攻击的早期版本 $26$ 不允许完全访问训练数据集 X0\mathcal{X}_{0}X0，并且对抗生成方法 ϕ\phiϕ 固定为快速梯度符号方法 (FGSM)。

实验上，我们表明混合黑盒攻击优于 Papernot 提出的原始攻击。我们的实验还表明，与边界攻击和纯黑盒攻击 $10, 25, 31, 32, 33, 34$ 相比，混合黑盒攻击在某些类型的随机化防御上效果更好。混合黑盒攻击的伪代码在算法 III-A 中给出，并在第 II-B 节中解释。

$htbp$ 混合黑盒攻击。 预言机 O\mathcal{O}O（即带有防御的分类器）使用合成模型 MMM 建模，该模型使用训练方法 TTT 训练 EEE 个周期，初始数据集为 X0⊆X0X_{0}\subseteq\mathcal{X}{0}X0⊆X0，数据增强参数为 λ\lambdaλ。最终的对抗样本使用攻击方法 ϕ\phiϕ 在扰动 ϵ\epsilonϵ 内从输入集 XcleanX{clean}Xclean 生成。

$1$ 输入 : O\mathcal{O}O, X0X_{0}X0, ϕ\phiϕ, λ\lambdaλ, EEE 和 XcleanX_{clean}Xclean
S0←{(x,O(x)) x∈X0}S_{0}\leftarrow\{(x,\mathcal{O}(x))\;x\in X_{0}\}S0←{(x,O(x))x∈X0}

// 基于初始随机参数 θ\thetaθ 训练模型
M(θ0)←T(M(θ),S0)M(\theta_{0})\gets T(M(\theta),S_{0})M(θ0)←T(M(θ),S0)
c∈{1,...,E}\mathbf{c}\in\{1,\ldots,E\}c∈{1,...,E}

// 使用 Jacobian 技术增强数据集 JFJ_{F}JF
Xe={x+λ⋅sgn(JF(x)):x∈Xe−1}X_{e}=\{x+\lambda\cdot sgn(J_{F}(x)):x\in X_{e-1}\}Xe={x+λ⋅sgn(JF(x)):x∈Xe−1}
Se←{(x,O(x)) : x∈Xe}∪Se−1S_{e}\leftarrow\{(x,\mathcal{O}(x))\;:\,x\in X_{e}\}\cup S_{e-1}Se←{(x,O(x)):x∈Xe}∪Se−1

// 在新数据集 SeS_{e}Se 上训练 MMM
M(θe)←T(M(θe−1),Se)M(\theta_{e})\gets T(M(\theta_{e-1}),S_{e})M(θe)←T(M(θe−1),Se)

// 使用 M(θE)M(\theta_{E})M(θE) 和攻击 ϕ\phiϕ 生成对抗样本
输出 : Xadv←{(x,ϕ(M(θE),ϵ;x,y)) : (x,y)∈Xclean}X_{adv}\leftarrow\{(x,\phi(M(\theta_{E}),\epsilon;x,y))\;:\;(x,y)\in X_{clean}\}Xadv←{(x,ϕ(M(θE),ϵ;x,y)):(x,y)∈Xclean}

边界黑盒攻击 $35$

在这种攻击中，对手具有对分类器的查询权限，并且一次只生成一个样本。攻击的主要思想是尝试使用二分搜索方法和边界点梯度近似来找到类别区域之间的边界。
基于分数的黑盒攻击

在文献中，这些攻击也称为基于零阶优化的黑盒攻击 $36$ 。对手自适应地查询防御，以基于无导数优化方法逼近给定输入的梯度。这个近似的梯度允许对手直接处理防御的分类器。这类攻击中的另一个攻击称为 SimBA（简单黑盒攻击） $37$ 。与所有之前提到的攻击不同，此攻击需要分数向量 f(x)f(x)f(x) 来发起攻击，而不仅仅是使用硬标签（hard label）。

===== 第 5 页 =====

在上面列举的攻击类型中，我们分析中唯一不考虑的黑盒攻击类型是基于分数的黑盒攻击。就像白盒攻击容易受到梯度掩蔽的影响一样，基于分数的黑盒攻击可以被一种掩蔽技术所中和 $30$ 。这意味着防御可能看起来对基于分数的黑盒攻击是安全的，但实际上并未提供真正的黑盒安全性。此外，已经注意到基于决策（硬标签）的黑盒攻击代表了一个更实际的对抗模型 $25$ 。因此，我们稍微将范围集中在其他三种黑盒变体上。

我们实现了纯黑盒攻击和混合黑盒攻击。在这两种攻击类型中，对抗样本都是使用六种不同的方法从合成模型生成的：FGSM $8$ 、BIM $38$ 、MIM $39$ 、PGD $27$ 、C&W $11$ 和 EAD $40$ 。我们还考虑了边界黑盒攻击。在这里，我们实现了原始边界攻击、Hop Skip Jump 攻击 (HSJA) $25$ 以及新提出的射线搜索攻击 (RayS) $34$ 。总的来说，这些攻击代表了十四种生成黑盒对抗样本的不同方式。

攻击成功率

对于分类器 CCC，我们将 X(C)\mathcal{X}(C)X(C) 定义为由训练数据集 X0\mathcal{X}_0X0 中正确被 CCC 分类的图像-标签对 (xi,yi)(x_i,y_i)(xi,yi) 组成的集合，即，

X(C)={(xi,yi)∈X0 : C(xi)=yi}.\mathcal{X}(C)=\{(x_i,y_i)\in\mathcal{X}_0\ :\ C(x_i)=y_i\}.X(C)={(xi,yi)∈X0 : C(xi)=yi}.

我们说 X(C)\mathcal{X}(C)X(C) 表示相对于分类器 CCC 的干净图像集合。

我们通过允许分类器 CCC 输出一个"不知道"符号 ⊥\perp⊥ 来扩展对分类器 CCC 的描述。如果 CCC 在输入 xxx 上计算得分向量 f(x)f(x)f(x)，而这些得分没有明显偏向任何标签，则可能发生这种情况。稍后我们也会将 ⊥\perp⊥ 解释为"对抗性"符号，表明它可能是一个对抗样本。

我们将分类器 CCC 相对于特定对抗样本生成技术 ϕ\phiϕ 的攻击成功率 α\alphaα 定义为

α(C,ϕ)=1−1∣X(C)∣∑(xi,yi)∈X(C)Pr⁡{C(ϕ(xi,yi))∈ $yi,⊥$ }.\alpha(C,\phi)=1-\frac{1}{|\mathcal{X}(C)|}\sum_{(x_i,y_i)\in\mathcal{X}(C)} \Pr\{C(\phi(x_i,y_i))\in $y_i,\\perp$ \}.α(C,ϕ)=1−∣X(C)∣1∑(xi,yi)∈X(C)Pr{C(ϕ(xi,yi))∈ $yi,⊥$ }.

这里，概率是关于 ϕ\phiϕ 和 CCC 使用的随机性（coin tosses）。攻击成功率反映了对抗样本成功的情况，即 CCC 将预测一个合法标签（即 ≠⊥\neq\perp=⊥），且该标签不等于正确的类别标签（即 ≠yi\neq y_i=yi）。

我们注意到 ϕ\phiϕ 是使用黑盒对手可用的信息单独训练/建模/生成的。这些信息可能包括集合 X0\mathcal{X}_0X0 和集合 X(C)\mathcal{X}(C)X(C)，并基于这些集合生成一个自生成的合成模型 M(θ)M(\theta)M(θ)，其中 θ\thetaθ 表示合成模型的参数。隐含地，ϕ\phiϕ 包含一个扰动参数 ϵ\epsilonϵ，表示对抗样本 ϕ(xi,yi)\phi(x_i,y_i)ϕ(xi,yi) 可能与原始图像 xix_ixi 的差异程度。

攻击成功率估计了能够成功生成对抗样本的 CCC 的干净图像的比例。成功意味着 C(ϕ(xi,yi))≠yiC(\phi(x_i,y_i))\neq y_iC(ϕ(xi,yi))=yi，即对抗样本 ϕ(xi,yi)\phi(x_i,y_i)ϕ(xi,yi) 被错误分类到一个不正确的标签，即使它接近原始图像 xix_ixi（相对于扰动参数 ϵ\epsilonϵ）。这里我们考虑所谓的非目标攻击，其中对手只对错误分类到某个其他合法但错误的标签感兴趣。（对于目标攻击，如果分类器将其标记为攻击者指定的目标类别标签，则该对抗样本被定义为成功。）在实践中，我们通过取一个子集 Xclean⊆X(C)X_{clean}\subseteq\mathcal{X}(C)Xclean⊆X(C) 并计算成功的对抗样本 ϕ(x,y),(x,y)∈Xclean\phi(x,y), (x,y)\in X_{clean}ϕ(x,y),(x,y)∈Xclean 的比例来估计 α(C,ϕ)\alpha(C,\phi)α(C,ϕ)。

以上内容适用于混合黑盒攻击，参见算法 1，如下所述。我们通过预言机 O\mathcal{O}O 表示对手有权访问的带有防御的分类器。攻击者从某个起始数据 X0⊆X0X_0\subseteq\mathcal{X}0X0⊆X0 开始，通常我们假设对防御者最坏的情况，即对手使用所有训练数据 X0=X0X_0=\mathcal{X}0X0=X0 作为起点。使用数据增强递归生成增强数据集 SeS_eSe，其中使用对预言机 O\mathcal{O}O 的查询来查找标签。某种训练方法 TTT（基于机器学习的数学优化）根据初始参数 θe−1\theta{e-1}θe−1 和 SeS_eSe 学习模型 MMM 的新参数 θe\theta_eθe。最终的合成模型 M(θE)M(\theta_E)M(θE) 可以通过使用白盒攻击方法 ϕ\phiϕ 进行攻击（这是可能的，因为黑盒对手知道参数 θE\theta_EθE，因此其合成模型 M(θE)M(\theta_E)M(θE) 的梯度预言机是可用的）。在最后一步，为 XcleanX{clean}Xclean 生成对抗样本，我们可以计算这些样本成功的比例------这估计了 α(C,ϕ(M(θE),ϵ;⋅))\alpha(C,\phi(M(\theta_E),\epsilon;\cdot))α(C,ϕ(M(θE),ϵ;⋅))。

III 防御

对抗性防御领域正在迅速扩展，几乎每个月都会发布多篇防御论文。1 要检查每一个提出的防御超出了本文的范围。相反，我们将分析集中在十个近期的、相关的和/或流行的防御方法上。在本节中，我们描述相关的防御方法、它们共同的安全要素以及为什么我们选择它们进行比较。我们考虑的相关防御包括：随机变换轰炸 (BaRT) $22$ 、The Odds are Odd (Odds) $23$ 、集成多样性 (ADP) $24$ 、Madry 的对抗训练 (Madry) $27$ 、基于多模型的防御 (Mul-Def) $21$ 、使用输入转换对抗对抗图像 (Guo) $20$ 、集成对抗训练：攻击与防御 (Tramer) $14$ 、混合架构 (Liu) $33$ 、通过随机化减轻对抗效应 (Xie) $18$ 、阈值网络（本文开发的基本概念验证防御）和屏障区 (BARZ)（本文提出的主要技术）。通常，对抗性防御可以根据几种潜在的防御机制进行划分。我们注意到这种划分

===== 第 6 页 =====

在其他防御论文中也很常见 $41$ 。虽然我们在此提供的分类定义绝非绝对，但它们为我们提供了一种更好地理解和分析该领域的方法。

多模型 - 防御使用多个分类器进行预测。分类器输出可以通过平均（例如 ADP）、从选择中随机挑选一个分类器（Mul-Def）或多数投票（混合架构）来组合。
图像变换 - 防御在分类前应用图像变换。在某些情况下，变换可能是随机的（Xie 和 BaRT）或固定的（Guo）。
对抗训练 - 训练分类器以正确识别对抗样本及其正确标签。Madry、Mul-Def 和 Tramer 都使用对抗训练。
对抗检测 - 如果样本被认为是经过对抗性操纵的，则防御输出空标签。Odds 采用了对抗检测机制，我们在本文中作为概念验证防御考虑的普通阈值网络也是如此。
随机化 - 防御在预测期间采用某种形式的随机化，攻击者事先不知道。BaRT 和 Xie 都在运行时对输入应用随机图像变换。

A. 随机变换轰炸 (BaRT)

$22$ 提出的随机变换轰炸 (BaRT) 是一种在分类前对输入 xxx 应用一组图像变换 i1,...,iri_1, \ldots, i_ri1,...,ir 的防御。BaRT 采用十种类型的图像变换：JPEG 压缩、图像扭曲、噪声注入、傅里叶变换扰动、缩放、色彩空间变化、直方图均衡化、灰度变换和去噪操作。对于每个输入 xxx，变换的数量、变换的顺序以及变换中的参数在运行时随机选择。

我们选择它的原因： 由于我们提出的防御 (BARZ) 也使用图像变换，BaRT 是一个自然的比较对象。在构建防御时，BaRT 在多个图像变换上训练单个网络。相比之下，我们的防御训练多个网络，每个网络在其自身较小的图像变换集上训练。比较这两种构建基于图像变换防御的不同方式是有意义的。

B. THE ODDS ARE ODD (ODDS)

The Odds are Odd 首次在 $23$ 中引入，作为检测对抗样本的统计检验。该检验背后的概念基于一个简单的观察：干净样本和对抗样本在 logits 层 I(⋅)I(\cdot)I(⋅) 具有不同的值。这里我们将 logits 层定义为 soft-max 层之前的层。当给定一个输入 xxx 时，该检验通过创建输入的多个副本（每个都添加了随机噪声）x^1,...,x^p\hat{x}_1, \ldots, \hat{x}_px^1,...,x^p 来工作。统计检验使用 I(x^1),...,I(x^p)I(\hat{x}_1), \ldots, I(\hat{x}_p)I(x^1),...,I(x^p) 作为输入来区分对抗样本和干净样本。

我们选择它的原因： 在黑盒设置中，对抗检测是使防御更强的一种可能方式，因为攻击者必须产生一个错误的类别标签并避免防御将输入标记为对抗性 (⊥\perp⊥)。在本文提出的防御 (BARZ) 中，我们也通过使用带多个分类器的阈值投票方法来进行检测。由于 Odds 试图实现的正是通过检测实现安全性，因此将统计检测方法与基于投票的检测防御（如 BARZ）进行比较是有意义的。

C. 通过促进集成多样性提高对抗鲁棒性 (ADP)

在防御中使用多个分类器是一个直接的概念，基于打破一个分类器集成比打破单个分类器更困难的想法。在 $24$ 中，他们通过专门训练一个分类器集成来进一步推进这个概念，以避免大多数分类器同时错误分类一个对抗样本的情况。在这种防御中，安全性在训练过程中通过使用自适应多样性促进 (ADP) 正则化器来实现。ADP 正则化器推动每个集成分类器的非最大预测相互正交。

我们选择它的原因： ADP 使用没有图像变换或对抗训练的分类器集成。另一方面，BARZ 使用带有图像变换的多个分类器。如果有可能在没有图像变换的集成中实现黑盒鲁棒性（例如仅通过像 ADP 中的特殊训练），这将否定在黑盒防御中进行特殊图像变换的需要。因此，测试 ADP 并将其与 BARZ 比较具有重要的黑盒安全意义。

D. MADRY 的对抗训练 (MADRY)

Madry 的对抗训练 $27$ 是一种广泛使用的防御方法，具有明确的安全目标。由于 CNNs 会错误分类对抗样本， $27$ 的作者提出在训练过程中生成对抗样本并随后学习正确分类它们。通常，对抗训练可以分为两个步骤。第一步，对于给定的干净数据集和分类器，防御者使用白盒对抗攻击 ϕ\phiϕ 推导出对抗数据集。第二步，使用对抗样本和原始干净标签训练分类器。在训练过程中重复这两个步骤多次，以创建一个鲁棒的对抗训练分类器。

我们选择它的原因： Madry 的对抗训练因其直观的设计和鲁棒的结果，是最常被接受的对抗性机器学习防御之一。虽然 Madry 对抗训练所基于的安全原则与 BARZ 没有直接重叠，但它仍然是一个防御标准，值得与之比较。

===== 第 7 页 =====

基于多模型的防御 (MUL-DEF)

在 $21$ 中，他们提出了一种针对白盒攻击的防御，基于多个具有相同架构的网络。 $21$ 的作者基于专门的训练技术开发了他们的防御。他们首先从一个在干净数据集 X\mathcal{X}X 上训练的分类器 C1C_1C1 开始。在 C1C_1C1 上进行白盒攻击 ϕC\phi_CϕC 以生成一组对抗样本 S1\mathcal{S}_1S1。一个新的训练集由原始数据集和对抗样本组成：X∪S1\mathcal{X} \cup \mathcal{S}_1X∪S1。这个新集用于训练下一个分类器 C2C_2C2。重复这个过程，使得分类器 CjC_jCj 在 X∪S1∪...∪Sj−1\mathcal{X} \cup \mathcal{S}1 \cup \ldots \cup \mathcal{S}{j-1}X∪S1∪...∪Sj−1 上训练。在预测期间，最终输出从分类器 C2,...,CmC_2, \ldots , C_mC2,...,Cm 中随机选择，其中 mmm 是 Mul-Def 中专门训练的分类器的数量。

我们选择它的原因： Mul-Def 与 BARZ 有重叠的安全概念。两者在防御中都使用多个模型，并且都试图创建不同的分类器（Mul-Def 通过特殊训练，BARZ 通过在变换数据上训练）。在 BARZ 的随机化形式中，使用模型输出的随机子集，类似于 Mul-Def。两种防御之间的主要区别在于 Mul-Def 不在模型之间进行任何投票，也不实现任何对抗检测。如果一个集成防御可以避免实现检测，这将明显提高防御的干净精度。这是因为不完美的检测方法会将一些干净样本标记为对抗样本（假阳性）。由于它们相似的安全概念，将 Mul-Def 与 BARZ 进行比较是合乎逻辑的。

F. 使用输入转换对抗对抗图像 (GUO)

在 $20$ 中，设计者为单个分类器选择一组可能的图像变换，并保持所选图像变换的选择是秘密的。这种防御（Guo）的主要安全思想是图像变换将充分扭曲对抗性噪声，使其不再导致分类器错误分类对抗样本。

我们选择它的原因： 虽然我们没有直接测试原始的 Guo 图像变换，但 Guo 防御背后的安全概念与 BARZ 中的单个网络相同。本质上，Guo 防御（单个网络和图像变换）中的安全原则是当分类器数量 m=1m = 1m=1 时 BARZ 的特例。由于 Guo 防御已经被提出，如果 BARZ-1（即 Guo 防御）已经提供了足够的安全性，那么再提出 BARZ 将是多余的。因此，有必要对 Guo 防御进行实验。

G. 集成对抗训练：攻击与防御 (TRAMER)

$14$ 的作者提出了另一种类型的对抗训练方法。在这种防御中，通过使用多种不同的攻击方法攻击多个网络来生成对抗样本。之后，设计者使用生成的对抗样本训练一个新的网络。 $14$ 的作者认为，这种对抗训练可以使对抗训练的网络对（纯）黑盒攻击更鲁棒，因为它使用来自不同来源（即预训练网络）的对抗样本进行训练。

我们选择它的原因： Tramer 防御具有与 BARZ 自然平行的安全概念。两种防御都依赖多个模型。在 BARZ 中，这些模型用于共识投票，在 Tramer 防御中间接依赖它们（用于生成新的对抗样本）。两种防御在设计时都考虑了黑盒对手。因此，在考虑黑盒威胁模型时，Tramer 防御是一个自然的测试选择。

H. 混合架构 (LIU)

在 $33$ 中，作者研究了 ImageNet 数据集上不同架构 CNN 之间的可迁移性。他们发现对抗样本并不总是在不同架构之间迁移，即被 C1C_1C1 错误分类的对抗样本并不总是被 C2C_2C2 错误分类。基于这项研究，可以提出一种由不同 CNNS C1,...,CmC_1, \ldots , C_mC1,...,Cm 组成的防御，每个 CNN 具有不同的结构。

我们选择它的原因： 虽然 $33$ 中没有直接提出，但混合架构防御的可行性问题源于 $33$ 的结果。由于 BARZ 使用多个模型，如果模型的架构是混合的，是否会对鲁棒性产生显著差异？通过测试混合架构防御（Liu），我们尝试从经验上回答这个问题。

I. 通过随机化减轻对抗效应 (XIE)

在 $18$ 中，开发了一种使用单个分类器的防御，在运行时对输入 xxx 应用随机图像变换 iri_rir。与 BaRT 或 BARZ 不同，此方法不需要在不同的图像变换 i1,...,ipi_1, \ldots , i_pi1,...,ip 上重新训练分类器。

我们选择它的原因： Xie 防御像 BARZ 一样使用图像变换。因此，这种防御提出了一个独特的竞争概念：通过随机化实现安全性，无需昂贵的重新训练。在黑盒对手下，是否可以在不重新训练的情况下获得这种鲁棒性，这就是我们在本文中研究 Xie 防御的原因。

J. 阈值网络 (VANILLAT)

阈值网络是本文展示的一种简单防御，用于突显创建鲁棒屏障区的挑战性本质。阈值网络是一种检测型防御，它使用普通分类器 CCC 和阈值 ttt。如果分类器 CCC 的最高概率 ppp 低于阈值 ttt，则该样本被标记为对抗样本：⊥\perp⊥。

我们选择它的原因： 当考虑屏障区防御时，第一个直觉可能是简单地阈值化一个普通分类器可能就有效。那将意味着可以在没有多个分类器或图像变换的情况下实现鲁棒性。我们开发阈值网络防御是为了

===== 第 8 页 =====

通过实验证明单个分类器的屏障区是不够的。

IV. 屏障区防御 (BARZ)

有这么多不同种类的防御，一个自然的问题是为什么我们要提出另一种？简而言之，答案是因为我们分析的当前防御方法中没有一种能在所有类型的黑盒攻击下表现良好，并在安全性和干净精度之间提供灵活的权衡。例如，像 Madry 这样的对抗训练网络在纯黑盒攻击下表现不佳（在 CIFAR-10 上鲁棒精度低于 65% $27$ ）。像 Xie 和 Mul-Def 这样的随机化防御对边界攻击效果很好，但在能适应随机化的混合黑盒攻击下会失败（我们在第六节展示了这方面的结果）。如果我们想提高它们的安全性，目前尚不清楚会多大程度影响干净精度。同样，如果我们想要更高的干净精度，而不完全放弃防御，也不明显如何实现这一点。在 BARZ 中，通过添加更多网络，安全性和干净精度之间的权衡是透明的。BARZ 也是唯一在所有类型黑盒攻击（纯、混合和边界）下表现良好的防御之一。

我们在第六节提供完整的实验结果来支持这些主张，并在附录中对每种防御相对于黑盒攻击进行单独分析。我们的主要重点是创建一种防御，以弥补其他提出方法的不足。我们努力创建一种高保真防御 (BARZ)，在安全性和干净精度之间提供灵活性。

A. 屏障区的安全原理

BARZ 防御基于屏障区的概念。屏障区是类别之间的区域，如果输入落在这个区域，它将被标记为对抗样本。对于任何新防御，第一个问题是为什么它有效，或者在这种情况下，为什么屏障区能提供安全性？这里我们给出这个概念背后的数学直觉。

假设我们有 mmm 个分类器 CjC_jCj，其对应的攻击成功率是 αj=α(Cj,θj)\alpha_j = \alpha(C_j, \theta_j)αj=α(Cj,θj)，其中对抗样本生成技术 θj\theta_jθj 特定于分类器 CjC_jCj。让我们构建一个新的分类器 CCC，它使用每个 CjC_jCj 来预测一个标签并输出多数决策。如果多个标签获得相同的多数票，那么 CCC 输出 ⊥\perp⊥，表示它不知道如何分配标签。要输出一个合法标签，CCC 需要有一个明确的多数票，并且该票数不被多个标签共享。

考虑一个针对 CCC 调整的对抗样本生成技术 ϕ\phiϕ。让投票数 VkV_kVk 定义为

Vk(xi,yi)=∣{1≤j≤m:Cj(ϕ(xi,yi))=k}∣V_k(x_i, y_i) = |\{1 \leq j \leq m : C_j(\phi(x_i, y_i)) = k\}|Vk(xi,yi)=∣{1≤j≤m:Cj(ϕ(xi,yi))=k}∣

（为简单起见，假设 CjC_jCj 和 ϕ\phiϕ 是确定性算法）。只有当 Vyi>VkV_{y_i} > V_kVyi>Vk 对于所有标签 k≠yik \neq y_ik=yi 成立时，分类器 CCC 才会输出正确的标签 yiy_iyi。如果输出一个不同于 yiy_iyi 且不同于 ⊥\perp⊥ 的标签，则对抗样本 ϕ(xi,yi)\phi(x_i, y_i)ϕ(xi,yi) 是成功的。也就是说，存在一个标签 y^∉{yi,⊥}\hat{y} \notin \{y_i, \perp\}y^∈/{yi,⊥}，使得对于所有合法标签 k≠y^k \neq \hat{y}k=y^，有 Vy^>VkV_{\hat{y}} > V_kVy^>Vk。

这表明差异

A(yi,k)=Vyi−VkA(y_i, k) = V_{y_i} - V_kA(yi,k)=Vyi−Vk

代表了在分类器 CCC 中选择 yiy_iyi 而非 kkk 的"优势"。通过使用符号 A(.,.)A(.,.)A(.,.) 并转化我们对成功对抗样本的描述，我们有攻击成功率 α=α(C,ϕ)\alpha = \alpha(C, \phi)α=α(C,ϕ) 等于

α=∣{(xi,yi)∈X(C)∣∂f∂x(xi,yi)>0∧⟨y^,k⟩>0}∣(1) \alpha = \left| \left\{ (x_i, y_i) \in \mathcal{X}(C) \mid \frac{\partial f}{\partial x}(x_i, y_i) > 0 \land \langle \hat{y}, k \rangle > 0 \right\} \right| \tag{1} α= {(xi,yi)∈X(C)∣∂x∂f(xi,yi)>0∧⟨y^,k⟩>0} (1)

其中 KKK 是所有合法类别标签连同 ⊥\perp⊥ 的集合。

这确立了在输出由多数决定的情况下，对多个标准分类器成功攻击的条件。我们现在展示 BARZ 中的两个安全原理如何增加攻击条件的难度。

绝对共识多数投票

在 BARZ 中，我们不使用简单的多数投票，而是使用绝对共识多数投票。这意味着如果并非所有分类器都同意同一个标签，则该样本被解释为对抗性/可疑的，标记为 ⊥\perp⊥，攻击失败。我们可以看到，这专门将 (1) 中成功攻击的阈值 >0> 0>0 更改为 ≥m\geq m≥m。请注意，虽然阈值现在更高了，但成功攻击的基本条件，即优势 A(y^,k)A(\hat{y}, k)A(y^,k)，其数值并未改变。我们的下一个安全原理处理基本条件。
输入变换

在 BARZ 中，每个分类器 CjC_jCj 实现其自己独特的秘密输入线性变换 ψj\psi_jψj。需要注意的是，在本小节中，我们抽象地讨论秘密变换 ϕj\phi_jϕj，而不指定具体的变换类型。理论上，这使我们能够开发对手攻击成功率的数学公式，而无需假设变换的类型。然而，对于实验和防御实现，图像变换很重要，我们在第 IV-B 节进一步讨论其选择。一旦应用了秘密输入线性变换 ψj\psi_jψj，就执行分类器 Cj′C_j'Cj′：

Cj′=Cj′∘ψj.C_j' = C_j' \circ \psi_j.Cj′=Cj′∘ψj.

采用个体变换的原因是为了进一步增加制作对抗样本 ϕ(xi,yi)\phi(x_i, y_i)ϕ(xi,yi) 的难度。文献中已经表明普通分类器具有高可迁移性 $33$ 。因此，使用没有变换的标准普通分类器（对所有 kkk，ψk\psi_kψk 是恒等函数）不会显著提高安全性的原因如下：如果

Cj′(ϕ(xi,yi))=y^≠yi,C_j'(\phi(x_i, y_i)) = \hat{y} \neq y_i,Cj′(ϕ(xi,yi))=y^=yi,

那么由于可迁移性，所有标准的普通分类器 Ck′C_k'Ck′ 很可能输出相同的错误标签 y^\hat{y}y^。

===== 第 9 页 =====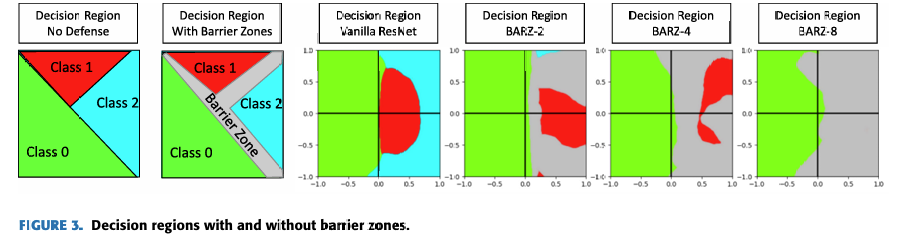

图 3. 有和无屏障区的决策区域。
（左上）无防御的决策区域（类别 0, 1, 2）。
（右上）带屏障区的决策区域（灰色区域表示被检测为对抗样本）。
（底部）CIFAR-10 图像在 2D 扰动空间中的决策边界可视化：

灰色：Vanilla ResNet（无防御）
绿色：BARZ-2
蓝色：BARZ-4
红色：BARZ-8
(绿色/蓝色/红色区域表示被正确分类或标记为对抗样本（BARZ 的灰色区），其他颜色区域表示错误分类)

这意味着使用普通分类器的绝对共识多数投票会产生高的攻击成功率 α\alphaα。参见 (1) 中绝对共识多数投票 ≥m\geq m≥m 的必要条件。

我们可以将 ϕ(xi,yi)\phi(x_i, y_i)ϕ(xi,yi) 重写为相应的干净图像和噪声：ϕ(xi,yi)=xi+ηi\phi(x_i, y_i) = x_i + \eta_iϕ(xi,yi)=xi+ηi。在这个公式下，我们可以将基本条件 A(y^,k)A(\hat{y}, k)A(y^,k) 重新表述为（利用 ψj\psi_jψj 的线性）：

∣ $1≤j≤m:Cj′(ϕ(xi,yi))=y\^$ ∣−∣ $1\leqj\leqm:Cj'(ϕ(xi,yi))=k$ ∣=∣ $1≤j≤m:Cj′(ψ(xi)+ψj(ηi))=y\^$ ∣−∣ $1\leqj\leqm:Cj'(ψ(xi)+ψj(ηi))=k$ ∣| $1 \\leq j \\leq m : C_j'(\\phi(x_i, y_i)) = \\hat{y}$ | - | $1 \\leq j \\leq m : C_j'(\\phi(x_i, y_i)) = k$ | = | $1 \\leq j \\leq m : C_j'(\\psi(x_i) + \\psi_j(\\eta_i)) = \\hat{y}$ | - | $1 \\leq j \\leq m : C_j'(\\psi(x_i) + \\psi_j(\\eta_i)) = k$ |∣ $1≤j≤m:Cj′(ϕ(xi,yi))=y\^$ ∣−∣ $1\leqj\leqm:Cj'(ϕ(xi,yi))=k$ ∣=∣ $1≤j≤m:Cj′(ψ(xi)+ψj(ηi))=y\^$ ∣−∣ $1\leqj\leqm:Cj'(ψ(xi)+ψj(ηi))=k$ ∣

(2)

从 (2) 式可以得出几个重要的结论。虽然变换 ψj\psi_jψj 在分类器之间变化，但对手制作的噪声 ηi\eta_iηi 并不改变。本质上，对于单个样本 xix_ixi，对手必须生成对变换集 ψ1,...,ψm\psi_1, \ldots, \psi_mψ1,...,ψm 不变的噪声 ηi\eta_iηi。具体来说，成功攻击的条件现在是：对于某个 y^∉ $yi,⊥$ \hat{y} \notin $y_i, \\perp$ y^∈/ $yi,⊥$ ，有 Cj′(ψ(xi)+ψj(ηi))=y^,...,Cm′(ψ(xi)+ψm(ηi))=y^C_j'(\psi(x_i) + \psi_j(\eta_i)) = \hat{y}, \ldots, C_m'(\psi(x_i) + \psi_m(\eta_i)) = \hat{y}Cj′(ψ(xi)+ψj(ηi))=y^,...,Cm′(ψ(xi)+ψm(ηi))=y^。也就是说，噪声 ψj(ηi)\psi_j(\eta_i)ψj(ηi) 必须同时愚弄所有 jjj 的分类器 CjC_jCj，而对手只能构造一个单一的噪声值 ηi\eta_iηi。

当我们将 (2) 式与绝对共识多数投票结合时，对手的最终攻击成功率可以简洁地写为：

∣(xi,yi)∈X(C)∃y^∈X(yi,⊥)∀j=1mCj′(ψ(xi)+ψj(ηi))=y^∣⋅∣X(C)∣\left| \frac{(x_i, y_i) \in X(C)}{\exists_{\hat{y} \in X(y_i, \perp)} \forall_{j=1}^m C_j'(\psi(x_i) + \psi_j(\eta_i)) = \hat{y}} \right| \cdot |X(C)| ∃y^∈X(yi,⊥)∀j=1mCj′(ψ(xi)+ψj(ηi))=y^(xi,yi)∈X(C) ⋅∣X(C)∣

在原始的多种分类器攻击公式 (1) 中，只需要大多数分类器将对抗样本 ϕ(xi,yi)\phi(x_i, y_i)ϕ(xi,yi) 错误分类为标签 y^\hat{y}y^，使得对于任何 k≠y^k \neq \hat{y}k=y^ 有 A(y^,k)>0A(\hat{y}, k) > 0A(y^,k)>0。在 BARZ 防御下，新的条件显然要求绕过所有分类器和每个变换。

B. 实现屏障区

在实践中，屏障区迫使对手添加幅度超过一定阈值的噪声 η\etaη 以克服屏障区。因为如果噪声变得对人类视觉可察觉，攻击就会失败，所以对手在 η\etaη 的幅度上受到限制。在许多情况下，这意味着对手可能无法克服屏障区，因此无法愚弄分类器。屏障区在图 3 的理论图和实际实验结果中都得到了展示。自然的问题是如何在分类器中实现屏障区？在本小节中，我们讨论可用于创建屏障区的不同技术。

多个分类器
屏障区可以通过使用多个分类器来创建。这种方法的一个朴素方法是简单地使用具有不同架构的 CNN。然而，我们表明仅仅使用不同的架构并不能产生安全性。具体来说，我们在结果中通过使用一个 VGG16 和一个 ResNet56 配合多数投票（我们将其表示为 Liu 防御）测试了这种防御。这在文献 $33$ 中也已被证明。架构防御未能提供安全性的其他例子包括 ADP 和 Mul-Def（我们在本文中测试了它们）。为了打破网络之间的可迁移性，我们为每个分类器引入了秘密的图像变换。我们由多个分类器（每个都有其自己的变换）组成的防御如图 4 所示。如图 4 所示，每个 CNN 有两个简单的独特秘密图像变换。第一个是固定的线性变换 c(x)=Ax+bc(x) = Ax + bc(x)=Ax+b，其中 AAA 是矩阵，bbb 是向量。

在线性变换之后，在图像馈入 CNN 之前应用一个调整大小操作 iii。对应于 ccc 和 iii 的 CNN 在干净数据 {i(c(x))}\{i(c(x))\}{i(c(x))} 上训练。使用多个 CNN，每个 CNN 都有自己的调整大小操作以及 AAA 和 bbb 分量，如图 4 所示。

从 $22$ 中我们知道，对抗样本对图像变换很敏感，这些变换要么扭曲图像中像素的值，要么改变像素的原始空间位置。需要注意的是，我们在本文中通过实验确定图像调整大小和线性变换可以降低可迁移性。然而，可能还有其他图像变换也能实现这一目标。

图像变换防御
在处理安全中的图像变换时，会出现几个简单的问题。例如，是否可以只使用一个带图像变换的网络而不重新训练？我们使用 Xie 的防御测试了这个概念（并且我们显示它在混合黑盒攻击下表现比 BARZ 差）。

===== 第 10 页 =====

是否只有一个带图像变换和重新训练的网络能工作？本质上我们测试了一个单一网络，带有一组变换（Guo）和一个在多个随机变换上重新训练的单一网络（BaRT）。这两种防御在混合黑盒攻击下的表现都比 BARZ 差。

另一个有效的问题是是否可以只采用对抗样本检测？我们通过以下方式测试这个假设：我们使用一个普通网络和一个置信度阈值，即任何低于某个特定置信度分数的样本都被标记为对抗样本。我们还测试了采用自身对抗检测方法的 Odds 防御。在第六节中，我们表明阈值化和 Odds 防御都无法胜过 BARZ。

需要注意的是，有可能进一步结合其他防御技术，如对抗训练、随机化部分图像变换或任何数量的其他技术。然而，本文的目标并非详尽测试每一种可能的防御组合。目标也不是测试文献中的每一种防御。这项工作的目标是提供一种针对黑盒对手的防御框架，该框架在干净精度和安全性之间提供清晰的权衡。

C. 屏障区图

在图 3 中，我们展示了针对 CIFAR-10 中单个图像的各种防御的屏障区图。这些图基于最初在 $33$ 中提出的决策区域图。在我们的图中，2D 网格上的每个点对应于图像 I′I'I′ 的类别标签。绿色表示 I′I'I′ 被正确分类，而红色和蓝色区域表示错误的类别标签。灰色表示分配了空（对抗性）类别标签。图像 I′I'I′ 由原始图像 III 生成：

I′=I+x⋅g+y⋅r.I' = I + x \cdot g + y \cdot r.I′=I+x⋅g+y⋅r.

这里 ggg 表示损失函数相对于 III 的梯度。在 (3) 式中，rrr 表示一个与 III 正交的归一化随机矩阵（注意 ggg 也被归一化）。变量 xxx 和 yyy 表示每个矩阵的幅度，由 2D 图中的坐标确定。

本质上，该图可以按以下意义解释：原点是未添加对抗扰动或随机噪声的原始图像的分类结果。当我们沿着 x 轴正向移动时，梯度矩阵 xxx 的幅度增加。仅沿 x 轴正向移动相当于 FGSM 攻击，其中通过添加损失函数的梯度（相对于输入）来修改图像。如果我们仅沿 y 轴移动，随机噪声矩阵 yyy 的幅度增加。这相当于向图像添加随机噪声。沿正 x 轴和 y 轴任意方向移动意味着我们正在向原始图像 III 添加对抗性扰动和随机噪声。离原点越远，xxx 和 yyy 的幅度越大，因此为创建 I′I'I′ 而施加的失真越大。

在防御使用多个网络 mmm 的情况下，每个网络 iii 将有不同的梯度矩阵 gig_{i}gi。为了补偿这一点，我们在归一化之前将各个梯度矩阵平均在一起以获得 ggg。需要注意的是，虽然图 3 中显示的图为屏障区概念提供了实验证明，但在实践中它们不能用于攻击 BARZ 防御。在创建这些图时，我们知道每个单独网络 iii 的个体梯度矩阵 gig_{i}gi。对于黑盒对手，只有防御的最终输出 O(x)\mathcal{O}(x)O(x) 是已知的。无法获得单个网络的输出。因此，据我们所知，在黑盒对抗模型下，不可能精确估计各个梯度 gig_{i}gi 来构建屏障区图。

! $在这里插入图片描述$ (https://i-blog.csdnimg.cn/direct/192727944f5f4ecc992e841a0fd138f7.png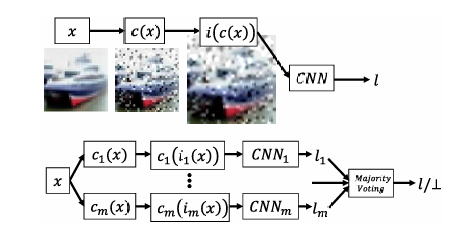

图 4. 顶部图片：BARZ 中带变换的单个网络设计。底部图片：由多个网络组成的完整 BARZ 防御。每个网络都有自己的变换集。最终输出通过绝对共识多数投票决定。如果未达成绝对共识，则该样本被标记为对抗样本。

V. 衡量防御性能

通常，在构建防御时，有两个主要方面需要考虑。第一个方面是安全性。在对抗性机器学习领域，安全性由鲁棒精度表示。在构建防御时，第二个方面是成本。在对抗性机器学习中，这种成本通常表现为干净精度的下降 γ\gammaγ。在理想情况下，安全性是免费的，即 γ=0\gamma = 0γ=0。在对抗性机器学习中，有充分文献证明鲁棒性（安全性）不是免费的。在干净精度和鲁棒性之间存在固有的权衡 $42, 43$ 。在这些情况下，自然的问题是，如果总是需要付出代价，我们如何评判一个防御？

在本文中，我们通过使用一个考虑鲁棒性和干净精度两者的指标来衡量这种权衡，从而回答这个问题。我们引入 δ\deltaδ-指标来正确理解以下因素的组合效应：

防御的干净精度从原始干净精度 ppp 下降到干净精度 pd=p−γp_d = p - \gammapd=p−γ 的下降量 γ\gammaγ (4)。这里，干净精度 ppp 对应于非恶意环境中无防御策略（普通方案）的精度，这是我们目前能达到的最佳精度。类似地，干净精度 pdp_dpd 代表在没有对手的情况下在非恶意环境中测量的防御精度。

卷 10, 2022

1460

===== 第 11 页 =====

（我们赋予"干净"额外的含义，即处于非恶意环境中。）

攻击者对防御的攻击成功率 α\alphaα。如果防御将经过对抗性操纵的图像识别为对抗样本，则它输出对抗性标签 ⊥\perp⊥，攻击不被视为成功。在定义 α\alphaα 时，我们将自己限制在那些防御（在其原始未受攻击形式下）能正确标记的图像的对抗样本上。攻击成功率则被定义为操纵这些图像使得防御产生不同于正确标签且不同于对抗性标签 ⊥\perp⊥ 的标签的对抗样本的比例。为完备起见，文献将鲁棒精度或防御成功率定义为 1−α1 - \alpha1−α。（我们注意到大多数防御无法将经过对抗性操纵的图像识别为对抗样本，并且没有对抗性标签作为可能的输出。）

在存在对手的情况下，防御的正确分类是以下之一：一个图像（可能在对抗性操纵后）被识别为其正确标签（意味着攻击无效）。或者，一个经过对抗性操纵的图像被赋予对抗性标签 ⊥\perp⊥（如果防御提供此可能性）。

在存在对手的情况下，防御正确/准确分类的概率等于 (p−γ)(1−α)(p - \gamma)(1 - \alpha)(p−γ)(1−α)（因为如果没有对手存在，防御会正确标记一部分 p−γp - \gammap−γ 的图像；而如果存在对手，这些图像中有一部分 α\alphaα 会被成功攻击）。换句话说，(p−γ)(1−α)(p - \gamma)(1 - \alpha)(p−γ)(1−α) 是在存在对手（恶意环境）时防御的精度。从没有防御的非恶意环境到有防御的恶意环境，精度的下降为：

δ=p−(p−γ)(1−α)=γ+(p−γ)α.\delta = p - (p - \gamma)(1 - \alpha) = \gamma + (p - \gamma)\alpha.δ=p−(p−γ)(1−α)=γ+(p−γ)α.

(5)

δ\deltaδ 可用于衡量不同防御的有效性，越小越好。如果两种防御提供大致相同的 δ\deltaδ，那么考虑它们的 (γ,α)(\gamma, \alpha)(γ,α) 对并选择具有较小 α\alphaα 或较小 γ\gammaγ 的防御是有意义的。

从纯粹的机器学习角度来看，为了使防御在非恶意环境中表现良好，我们希望 γ\gammaγ 非常小，或者等价地，pdp_dpd 接近 ppp。从纯粹的安全角度来看，为了使防御在恶意环境中表现良好，我们希望 δ\deltaδ 小。因此，为了正确比较防御，我们关注元组 (δ=γ+(p−γ)α,pd=p−γ)(\delta = \gamma + (p - \gamma)\alpha, p_d = p - \gamma)(δ=γ+(p−γ)α,pd=p−γ)，其中 α\alphaα 对应于文献中已知最佳攻击的攻击成功率。请注意，普通方案也可以在恶意环境中考虑，这将对应于某个 (δvan,pd=p)(\delta_{van}, p_d = p)(δvan,pd=p)。显然，导致 δ≥δvan\delta \geq \delta_{van}δ≥δvan 的防御并没有比根本不实施任何防御（即普通方案）有所改进。

在理想情况下 δ=0\delta = 0δ=0，即攻击总是失败 (α=0\alpha = 0α=0) 且使用防御没有成本 (γ=0\gamma = 0γ=0)。由于对抗性攻击，α>0\alpha > 0α>0，因此这种情况不会发生。因此，我们寻找具有最小 δ\deltaδ 的防御，例如，一个同时具有低 α\alphaα 和低 γ\gammaγ 的防御。如果两种防御具有相似的 δ\deltaδ 值，我们可以简单地考虑具有更好干净精度的那个，这正是我们在本文中所做的。需要注意的是，δ\deltaδ 指标只是理解鲁棒性和干净精度之间权衡的一种方式。它绝不是决定性的或唯一的方式。在本文中，我们专注于使用 δ\deltaδ 指标来衡量防御，因为它能够简洁地捕获两组信息：α\alphaα（安全性）和 γ\gammaγ（成本）。对于那些对其他指标感兴趣的人，我们在附录中以图表形式提供了本文涵盖的所有攻击和防御的所有精度测量结果。

VI 实验结果

在本节中，我们提供实验结果以展示 BARZ 防御的有效性。我们还展示了我们提出的混合黑盒攻击带来的改进。我们在两个流行的数据集 Fashion-MNIST $44$ 和 CIFAR-10 $45$ 上进行了实验。与文献中报告的其他结果不同，对于每种防御，只要可能，我们都使用相同的网络架构构建它。我们将防御应用于相同的数据集，并在同一组攻击下运行每种防御。这使我们能够提供前所未有的自适应黑盒攻击结果的比较。我们还在 Github 上提供了与实验相关的代码：https://github.com/MetaMain/BARZ。

A. 混合黑盒攻击

如第三节所述，我们的混合黑盒攻击是 Papernot 攻击的扩展。原始论文 $26$ 仅使用单一方法生成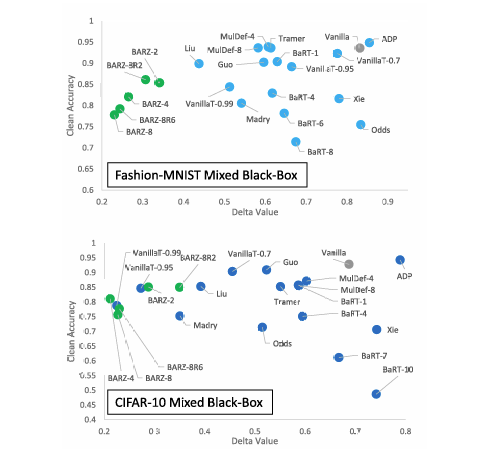

图 5. 混合黑盒攻击的 δ\deltaδ 指标与干净精度 pd=p−γp_d = p - \gammapd=p−γ 的关系图。BARZ 结果以绿色显示，普通方案结果以灰色显示。

===== 第 12 页 =====

图 6. 非目标混合黑盒攻击（上）、非目标纯黑盒攻击（中）和非目标边界攻击（下）的鲁棒精度。注意：如果列出了防御但没有显示条形，则意味着该防御对该攻击的鲁棒精度为 0%，即攻击对该防御 100% 有效。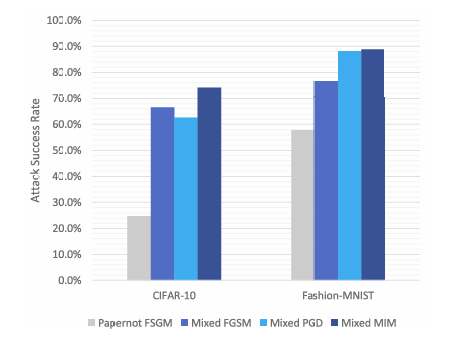

图 7. 原始 Papernot 攻击和本文提出的新混合黑盒攻击的攻击成功率。重现实验的进一步比较和完整描述在附录中给出。

对抗样本，即快速梯度符号方法 (FGSM)。我们在图 7 中比较了 Papernot 攻击和混合黑盒攻击在 ∥l∥∞\|l\|_{\infty}∥l∥∞ 范数下的结果，CIFAR-10 的最大扰动 ϵ=0.05\epsilon = 0.05ϵ=0.05，Fashion-MNIST 的最大扰动 ϵ=0.1\epsilon = 0.1ϵ=0.1。使用测试集中的 1000 个样本测量攻击成功率。总体而言，通过向对手提供更多数据，在普通网络（无防御）上的非目标攻击成功率在 CIFAR-10 上可提高 49.4%，在 Fashion-MNIST 上提高 31.1%。这些结果的更多实验细节在附录中给出。有些人可能会质疑拥有训练数据访问权限的对手的实用性。然而，作为防御设计者，我们希望考虑最强大的硬标签黑盒对手。因此，混合黑盒攻击显然对于防御验证是必要的。

B. 纯黑盒和边界攻击

除了混合黑盒攻击，我们还考虑了纯黑盒攻击和边界攻击。这些攻击中的每一种都可以根据对抗样本的生成方式进一步分类。对于纯黑盒和混合黑盒攻击（本文提出），我们使用六种不同的对抗生成方法（FGSM、IFGSM、PGD、MIM、C&W 和 EAD）。对于纯黑盒攻击，我们使用相同的生成方法集（但与攻击结合使用的模型不是自适应训练的）。对于边界攻击，我们考虑 HSJA 和 RayS。这总共代表了四种类型的黑盒攻击和 14 种生成对抗样本的方式。对于 CIFAR-10，我们允许的最大扰动是 ϵ=0.05\epsilon = 0.05ϵ=0.05，对于 Fashion-MNIST，最大扰动是 ϵ=0.1\epsilon = 0.1ϵ=0.1。对于 RayS，我们允许每个样本 10,000 次查询；对于 HSJA，我们使用可变查询风格的攻击（我们在附录中详细解释）。注意在表 2 中，某些攻击对某些防御不适用。这只发生在针对 2 种防御（BaRT 和 Odds）的边界攻击上。这是由于边界攻击运行时非并行化预测的计算复杂性问题。我们在附录中对此以及所有攻击的精确攻击细节进行了充分解释。

C. 防御

我们实验了 11 种防御（BARZ、普通阈值化、Guo、Liu、ADP、Xie、Madry、Tramer、Mul-Def、BaRT 和 Odds）。在网络架构方面，我们在 CIFAR-10 防御中使用 ResNet56 $46$ ，在 Fashion-MNIST 防御中使用 VGG16 $47$ 。需要注意的是，这里报告的结果并不总是与文献结果完全相同。这是由于架构和数据集的差异。例如，BaRT 的作者从未发布过其防御的 CIFAR-10 版本，因此我们的 BaRT 实现将具有与他们为 ImageNet 报告的不同的精度。同样，Madry 原始的 CIFAR-10 防御是使用 Wide ResNet 训练的，而我们使用 ResNet56V2。我们尽可能为每种防御使用相同的基础架构和相同的数据集，以使我们的比较尽可能有效。由于篇幅有限，我们无法在此描述每种防御的完整实现细节。我们鼓励感兴趣的读者查阅附录以获取更多细节。

===== 第 13 页 =====

表 2. 所有防御在不同攻击下的 δ\deltaδ 值和干净精度。每个类别的最佳 δ\deltaδ 以粗体显示。注意每种攻击类型（例如 HSJA, RayS, 混合黑盒 MIM, 纯黑盒 PGD 等）的鲁棒精度在附录中给出。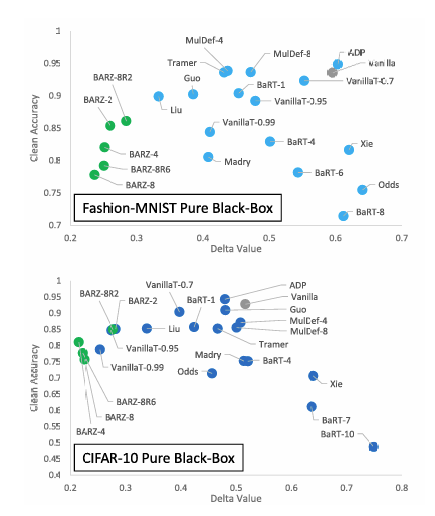

图 8. 纯黑盒攻击的 δ\deltaδ 指标与干净精度 pd=p−γp_d = p - \gammapd=p−γ 的关系图。BARZ 结果以绿色显示，普通方案结果以灰色显示。

BARZ 和阈值化防御
在本文中，我们实验了 BARZ 以及一种我们称之为普通阈值化的朴素防御。一个常见的误解是，仅仅通过阈值化普通分类器的输出（即如果网络对其预测不自信，则将样本标记为对抗性），就可以减轻所有黑盒攻击。我们提供了 70%、95% 和 99% 阈值网络的结果，以表明事实并非如此。
对于 BARZ，我们通过图像变换实现屏障区。具体来说，每个网络都有一个从映射 c(x)=Ax+bc(x) = Ax + bc(x)=Ax+b 中选择的图像变换。我们在附录中解释了如何根据数据集选择随机的 AAA 和 bbb。我们可以将图像变换 cj(x)c_j(x)cj(x) 视为添加到构成第 jjj 个 CNN 的层上的额外随机固定层。我们测试了三种这样的设计：一种有 8 个网络 (BARZ-8)，每个使用不同的图像调整大小操作：32 到 32, 40, 48, 64, 72, 80, 96, 104。第二种有 4 个网络 (BARZ-4)，是 8 个网络中使用图像调整大小操作 32 到 32, 48, 72, 96 的子集。第三种有 2 个网络 (BARZ-2)，是 8 个网络中使用图像调整大小操作 32 到 32 和 104 的子集。
我们还考虑了 BARZ 的随机化版本，我们将其表示为 BARZ-xRy。在此版本中，使用 yyy 个网络（从 xxx 个网络中选择）的子集来对样本进行绝对多数投票。例如，在 BARZ-8R2 中，每次提交样本时，随机选择八个网络中的两个来分类该样本。

D. 实验分析

我们论文的主要结果在表 2 中给出，用于 CIFAR-10 和 Fashion-MNIST，鲁棒精度在图 6 中直观显示。我们根据防御最弱的攻击（即具有最低鲁棒精度）计算每种防御的 δ\deltaδ 指标。例如，如果 BARZ-8 防御对 RayS 的鲁棒精度为 60%（60% 的对抗样本未能愚弄防御），对 HSJA 的鲁棒精度为 39%，则使用 HSJA 来计算 BARZ-8 的边界 δ\deltaδ 指标。纯黑盒攻击、混合黑盒攻击和边界攻击对手的最坏情况 δ\deltaδ 指标结果在图 5、8 和 2 中直观展示。

在性能方面，我们提出的防御 (BARZ) 在 CIFAR-10 和 Fashion-MNIST 上都优于其他所有防御。在 CIFAR-10 上，BARZ-4 为 δ\deltaδ 混合和 δ\deltaδ 纯提供了安全性和精度之间的最佳权衡，而 BARZ-8 具有最佳的鲁棒精度（混合攻击下 92.6%，纯攻击下 92.8%）。对于边界攻击，BARZ-8R6 也为 CIFAR-10 提供了最佳权衡以及最佳鲁棒精度 (87%)。同样，对于 Fashion-MNIST，BARZ-8 对混合和纯黑盒攻击具有最低的 δ\deltaδ。对于 Fashion-MNIST，BARZ-8 还具有最佳的纯和混合鲁棒精度，分别为 90.6% 和 89.9%。对于 Fashion-MNIST 的边界攻击，我们可以看到 BARZ-8R2 提供了最佳权衡，但 Madry 提供了略好的鲁棒精度（Madry 为 96%，BARZ-8R2 为 92%）。对于那些对传统鲁棒精度测量感兴趣的人，我们在图 1 中给出了总体结果。该图显示了每种防御在所有黑盒攻击中的最小鲁棒精度。我们只能在本节中总结主要结果。在附录中，我们深入比较了 11 种防御的结果。

VII 结论

在本文中，我们通过提供一种新的黑盒攻击和一种基于屏障区的新型黑盒防御，推进了对抗性机器学习领域的发展。我们的新攻击经实验证明比原始的 Papernot 攻击更强。它还在 Xie 和 Mul-Def 等防御上优于边界攻击和纯黑盒攻击。其次，也是最重要的，我们开发了一种新的基于屏障区的防御。我们的防御在纯黑盒、混合黑盒和基于边界的黑盒攻击下，优于我们测试的所有其他 10 种防御方法。在本文测试的所有黑盒攻击和数据集上进行比较时，我们最佳的防御配置在 CIFAR-10 和 Fashion-MNIST 上提供了超过 85% 的鲁棒精度，与次优防御相比提高了超过 30%。总的来说，我们开发了第一个屏障区防御 (BARZ)，实验证明其对 14 种不同类型的黑盒攻击具有鲁棒性。

附录 A 实验防御结果

在本节中，我们提供补充实验结果，包括：

- 目标和非目标混合黑盒攻击，
- 目标和非目标纯黑盒攻击，以及
- 边界攻击------非目标 HopSkipJump $25$ 和 RayS $34$ 。

我们在十种不同的防御策略上运行这些攻击：随机变换轰炸 (BaRT) $22$ 、The Odds are Odd (Odds) $23$ 、集成多样性 (ADP) $24$ 、Madry 的对抗训练 (Madry) $27$ 、基于多模型的防御 (Mul-Def) $21$ 、使用输入转换对抗对抗图像 (Guo) $20$ 、集成对抗训练：攻击与防御 (Tramer) $14$ 、混合架构 (Liu) $33$ 、通过随机化减轻对抗效应 (Xie) $18$ 、阈值网络（本文开发的基本概念验证防御）和屏障区 (BARZ)，使用 CIFAR-10 $45$ 和 Fashion-MNIST $44$ 数据集。对抗样本的生成是通过在合成模型（从纯黑盒或混合黑盒攻击获得的模型）上运行白盒攻击来完成的。用于对抗样本生成的六种白盒攻击是 FGSM $8$ 、BIM $38$ 、MIM $39$ 、PGD $27$ 、C&W $11$ 和 EAD $40$ 。我们还在边界黑盒攻击（Hop Skip Jump $25$ 和 RayS $34$ ）下测试了防御。

我们本节首先讨论防御在本文黑盒攻击下的鲁棒性。

A. 防御的鲁棒性

图 6 和图 9 分别代表了使用 Fashion-MNIST 和 CIFAR-10 数据集时，防御在不同黑盒攻击下的鲁棒精度。对于目标攻击，图 10 展示了防御在二维（干净精度 vs delta (δ\deltaδ)）上的表现。我们从这些图中得出以下主要观察结果：

混合黑盒攻击比纯黑盒攻击更强，非目标攻击比目标攻击更强大。与纯黑盒攻击相比，混合黑盒攻击被提供了更多关于目标模型的信息（原始训练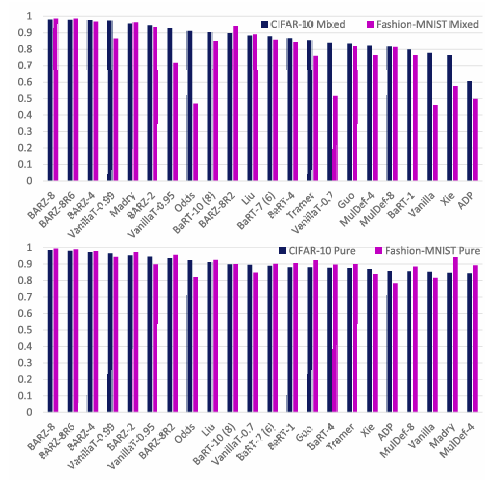

图 9: 目标混合黑盒攻击（上）和目标纯黑盒攻击（下）的鲁棒精度。

===== 第 15 页 =====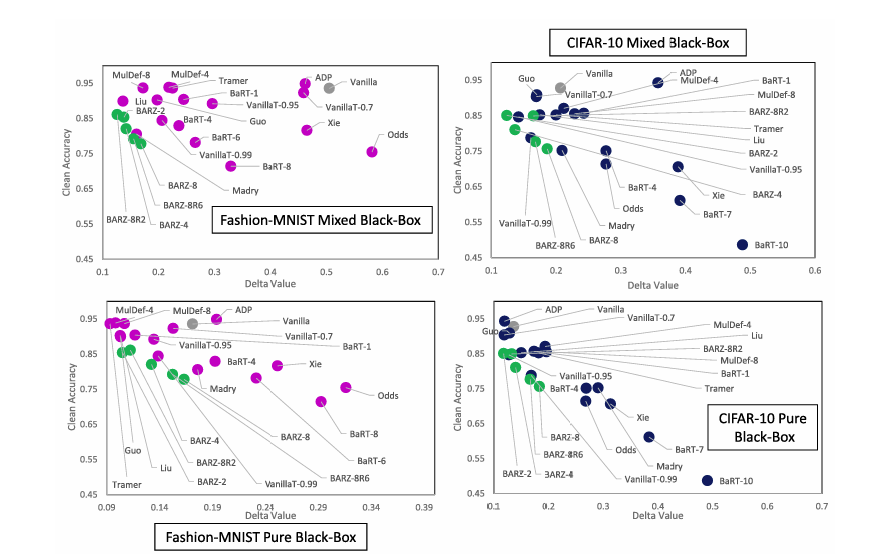

图 10. 目标混合黑盒攻击和目标纯黑盒攻击的 δ\deltaδ 指标与干净精度关系图。BARZ 结果以绿色显示，普通方案结果以灰色显示。

数据和对目标模型的查询权限以标记生成的合成数据）；因此混合黑盒攻击应该比纯黑盒攻击更强。因为目标攻击可以被视为比非目标攻击有更多约束的优化问题，所以目标攻击应该需要更多的努力来运行，因此威力较小。

目标纯黑盒攻击似乎不是一个强大的攻击模型。这得到了普通方案（根本不实施任何防御）已经提供了非常好的鲁棒性（即，它已经对目标纯黑盒攻击具有很高的防御精度）这一事实的支持。因此，几乎所有考虑的防御在这种威胁模型下都提供了良好的鲁棒性和干净精度。这解释了为什么在图 10 的目标纯黑盒攻击图中，防御相对集中。
如上所述和讨论，混合黑盒攻击比纯黑盒攻击更强。这解释了为什么一部分考虑的防御对于目标混合黑盒攻击（如图 10 所示）仍然能显著优于普通方案。
对于非目标边界攻击，有许多防御的鲁棒精度为 0%。因此，我们在图 6 中没有看到它们的条形图，例如 Vanilla、VanillaT-0.7 等具有 0% 的鲁棒精度。
图 5、8、2、6、9 和 10 中最有趣和最重要的观察结果如下：

a) 存在一组防御，它们享有高鲁棒性和高干净精度，即防御位于具有小 δ\deltaδ 值和高干净精度的左上角。

b) BARZ 防御在以上提到的任何场景中都属于该组。

这些观察结果表明，在所有场景中，BARZ 系列与其他防御相比提供了良好的鲁棒性和干净精度。

我们在接下来的 Fashion-MNIST 和 CIFAR-10 章节中提供更详细的攻击和防御结果。请注意，接下来两节中的所有详细结果已在图 5、8、2、6、9 和 10 中可视化，关于这些详细结果的最重要讨论和观察已在上文总结。

B. FASHION-MNIST：攻击与防御

Fashion-MNIST 的结果在表 3、4、5、6 和 7 中描述。回顾 δ\deltaδ 指标的公式：

δ=γ+(p−γ)α=p−(p−γ)(1−α)=p−pd⋅β,\delta = \gamma + (p - \gamma)\alpha = p - (p - \gamma)(1 - \alpha) = p - p_d \cdot \beta,δ=γ+(p−γ)α=p−(p−γ)(1−α)=p−pd⋅β,

其中 ppp 是普通分类器（即根本没有防御且无对抗存在）的干净精度，γ\gammaγ 是干净精度的下降，即 γ=p−pd\gamma = p - p_dγ=p−pd（pdp_dpd 代表没有攻击者存在时防御的干净精度），α\alphaα 是攻击者对防御的攻击成功率，β\betaβ 是鲁棒精度或防御成功率（也称为防御精度），等于 1−α1 - \alpha1−α。

===== 第 16 页 =====

K. Mahmood 等人：击败黑盒：用于对抗样本防御的屏障区
表 3. Fashion-MNIST 目标混合黑盒攻击结果。注意 β\betaβ 列指的是所有目标混合黑盒攻击中的最小鲁棒精度。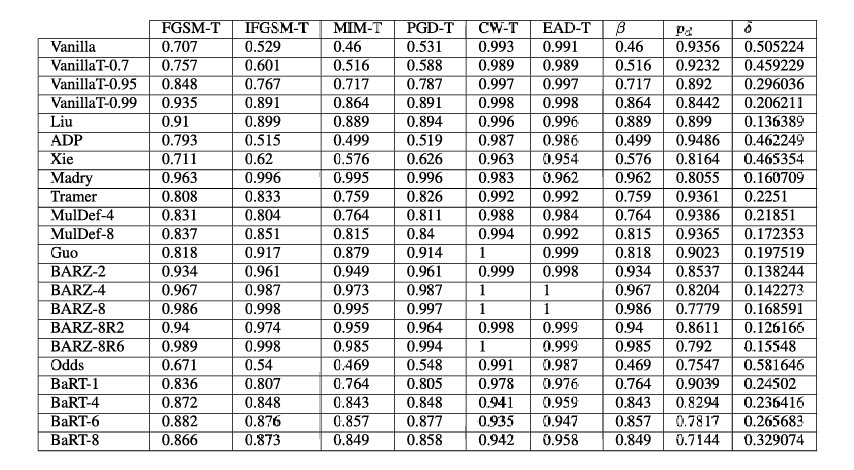

表 4. Fashion-MNIST 目标纯黑盒攻击结果。注意 β\betaβ 列指的是所有目标纯黑盒攻击中的最小鲁棒精度。

对于 Fashion-MNIST 和 CIFAR-10，ppp 分别为 0.9356 和 0.9278。δ\deltaδ 的值是通过结合普通分类器的 ppp 和所考虑防御的 pdp_dpd，并查看在给定防御上所有已实施攻击中最佳的攻击（这对应于所考虑的特定攻击集中攻击成功率 α\alphaα 的最大值，类似地，对应于各种防御成功率 β\betaβ 的最小值）来计算的。例如，表 3 中 BARZ-8 的 δ\deltaδ 指标计算如下：我们将 p=0.9356p = 0.9356p=0.9356、pd=0.7779p_d = 0.7779pd=0.7779 以及所有（当前已知）目标混合黑盒攻击中的最小 β=0.986\beta = 0.986β=0.986（在本例中对应于 FGSM-T 攻击）代入公式（方程 6）求 δ\deltaδ。结果为 δ=0.168591\delta = 0.168591δ=0.168591。

讨论：我们从上述表中得出以下观察结果：

BARZ 系列在任何攻击场景下都实现了最小的 δ\deltaδ。图 5、8、2 和 10 反映了这一事实。
许多防御（如 Guo、Liu、ADP、Tramer）具有非常高的干净精度（即接近普通分类器的干净精度），但具有非常大的 δ\deltaδ。如果我们仔细查看图 6 和 9 或表 3、5、6 和 7 中呈现的结果，我们可以看到它们容易受到黑盒攻击。换句话说，它们不提供安全性。
通过结合干净精度的下降 γ\gammaγ 和鲁棒精度 β\betaβ 的增加，δ\deltaδ 指标可用于理解防御在攻击者存在下的表现。为了进行更详细的评估，我们需要分别查看攻击成功率 α\alphaα（或等效地，鲁棒精度 β\betaβ）和防御的干净精度 pdp_dpd。

===== 第 17 页 =====

表 5. Fashion-MNIST 非目标混合黑盒攻击结果。注意 β\betaβ 列指的是所有非目标混合黑盒攻击中的最小鲁棒精度。

表 6. Fashion-MNIST 非目标纯黑盒攻击结果。注意 β\betaβ 列指的是所有非目标纯黑盒攻击中的最小鲁棒精度。

从表 3、4、5 和 6 我们得出结论：混合黑盒攻击比纯黑盒攻击更有效，非目标黑盒攻击比目标攻击更强。当查看表 7 时，边界攻击比混合和纯黑盒攻击强得多。
BARZ 可以通过调整防御中分类器的数量来实现防御者精度 pdp_dpd 和攻击者成功率 α\alphaα 的不同组合。
BARZ-RZ、Madry 和 MulDef 对边界攻击具有最小的 δ\deltaδ 值。对于 BARZ 和 MulDef 防御，原因在于对于给定的输入 xxx，在每次评估时，这些防御会引入一些随机性。因此，输出类别标签可能会改变。这强烈影响了边界攻击的效率，这些攻击需要精确估计许多图像的梯度（而由于引入的随机性，这些估计变得不太准确）。

C. CIFAR-10：攻击与防御

CIFAR-10 的结果在表 8、9、10、11 和 12 中描述。

===== 第 18 页 =====

表 7. Fashion-MNIST 非目标边界攻击结果。注意 β\betaβ 列指的是所有边界攻击中的最小鲁棒精度。

讨论：我们从上述表中得出以下观察结果（与 Fashion-MNIST 相似，第 6 项略有不同）：

BARZ 系列在任何攻击场景下都实现了最小的 δ\deltaδ。图 5、8、2 和 10 反映了这一事实。
许多防御（如 Guo、Liu、ADP、Tramer）具有非常高的干净精度（即接近普通分类器的干净精度），但具有非常大的 δ\deltaδ。如果我们仔细查看图 6 和 9 或表 8、10、11 和 12 中呈现的结果，我们可以看到它们容易受到黑盒攻击。换句话说，它们不提供安全性。
通过结合干净精度的下降 γ\gammaγ 和鲁棒精度 β\betaβ 的增加，δ\deltaδ 指标可用于理解防御在攻击者存在下的表现。为了进行更详细的评估，我们需要分别查看攻击成功率 α\alphaα（或等效地，鲁棒精度 β\betaβ）和防御的干净精度 pdp_dpd。
从表 8、9、10 和 11 我们得出结论：混合黑盒攻击比纯黑盒攻击更有效，非目标黑盒攻击比目标攻击更强。当查看表 12 时，边界攻击比混合和纯黑盒攻击强得多。
BARZ 可以通过调整防御中分类器的数量来实现防御者精度 pdp_dpd 和攻击者成功率 α\alphaα 的不同组合。
BARZ-8R6/2、Xie 和 MulDef 对边界攻击具有最小的 δ\deltaδ 值。原因在于对于给定的输入 xxx，在每次评估时，这些防御会引入一些随机性。因此，输出类别标签可能会改变。这强烈影响了边界攻击的效率，这些攻击需要精确估计许多图像的梯度（而由于引入的随机性，这些估计变得不太准确）。

附录 B

实验攻击结果

正如我们在论文主体部分提到的，混合黑盒攻击可以被视为 Papernot 攻击的扩展。在本节中，我们使用 CIFAR-10 数据集提供实验证据来支持我们的主张。在图 11 中，我们展示了攻击成功率作为训练数据函数的图形表示。图的 x 轴是攻击开始时用于构建合成模型的训练数据百分比。图的 y 轴是攻击在普通（无防御）模型上的成功率。

对于这个实验，我们固定了几个变量以便进行比较。我们使用 FGSM 攻击在合成模型上生成对抗样本，ϵ=0.05\epsilon = 0.05ϵ=0.05。对于所有实验，我们将攻击中的迭代次数固定为 N=4N = 4N=4，λ=0.1\lambda = 0.1λ=0.1。在 Papernot 对 MNIST 分类器的原始攻击中，使用了 0.3% 的原始训练数据。我们显示，随着训练数据（以及后续查询）量的增加，攻击成功率也会增加。当训练数据百分比达到 100% 时，我们就得到了我们称之为混合黑盒攻击的结果。这代表了攻击成功率的显著提高。在我们的 CIFAR-10 实验中，它从 24.7% 增加到 66.6%，攻击成功率提高了 41.9%。

在某些防御上，混合黑盒攻击也优于其他攻击。例如，考虑随机化的 Xie 防御。在非目标边界攻击下，CIFAR-10 的鲁棒精度为 85%。然而，在非目标混合黑盒攻击下，鲁棒精度最低，仅为 26.2%。同样，混合黑盒攻击在 MulDef-4 和 MulDef-8 上优于边界攻击（尽管纯黑盒攻击在这里以微弱的 1% 优势最强）。如果我们考虑 Fashion-MNIST，我们也可以看到混合黑盒攻击在其上表现优于其他攻击的防御。在 Fashion-MNIST 上，Xie、MulDef 和 Madry 防御的最低鲁棒精度是在混合黑盒攻击下获得的。

总结一下，我们在此分析的目的有两个。首先，通过实验，我们表明在条件相同的情况下，混合黑盒攻击明显优于原始的 Papernot 攻击。其次，我们表明混合黑盒攻击是针对某些防御的最有效攻击。需要明确的是，我们不声称拥有普遍最强的黑盒攻击。我们只是表明，由于不同的防御采用不同的防御技术，某些黑盒攻击将比其他攻击更有效。因此，测试广泛的黑盒攻击（正如本文所做的那样）是必要的。在这个要测试的攻击范围中，混合黑盒攻击显然对于防御验证是必要的。

===== 第 19 页 =====

表 8. CIFAR-10 目标混合黑盒攻击结果。注意 β\betaβ 列指的是所有目标混合黑盒攻击中的最小鲁棒精度。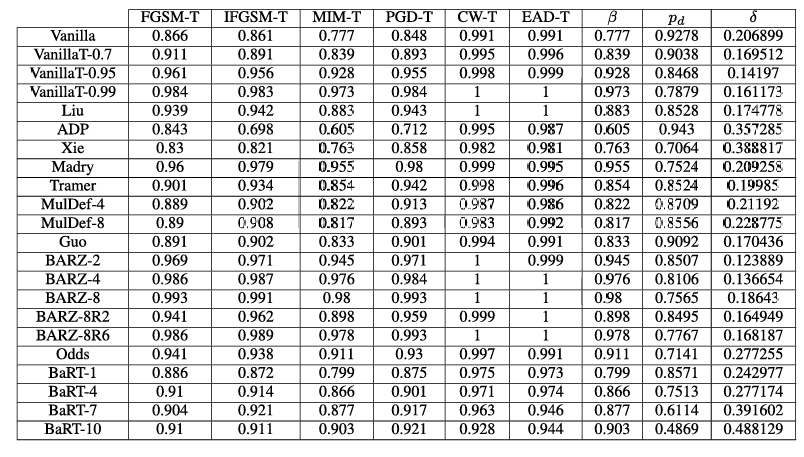

表 9. CIFAR-10 目标纯黑盒攻击结果。注意 β\betaβ 列指的是所有目标纯黑盒攻击中的最小鲁棒精度。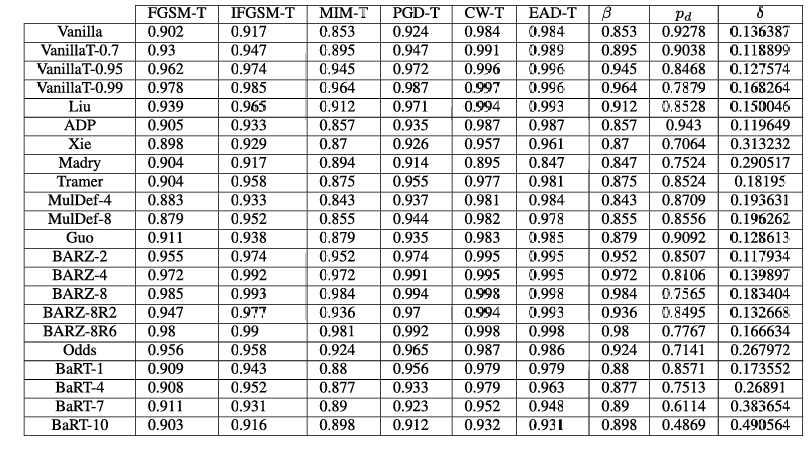

附录 C

对抗攻击描述

D. 纯黑盒和混合黑盒攻击

正如我们在主要论文中提到的，混合黑盒攻击是 $26$ 提出的原始攻击的扩展。这里我们将 ggg 表示为来自 $26$ 的基于预言机的黑盒攻击的合成网络。攻击者有权访问分类器本身，该分类器在查询时返回一个分数向量或分数最大的标签------我们称之为黑盒预言机。预言机访问在此情况下提供查询 xxx 的类别标签 F(f(x))F(f (x))F(f(x))（而不是分数向量 f(x)f (x)f(x)）。最初，攻击者拥有部分训练数据集 XXX，即他们知道 D={(x,F(f(x))):x∈X0}D = \{(x, F(f (x))) : x \in X_0\}D={(x,F(f(x))):x∈X0}（对于某个 X0⊆XX_0 \subseteq XX0⊆X）。注意，对于单次迭代 N=1N = 1N=1 的攻击简化为一种不需要任何预言机访问 O\mathcal{O}O 来构建合成模型的算法；这种简化算法用于纯黑盒攻击 $10$ , $33$ , $48$ 。

在混合黑盒攻击中，我们假设算法 1 中最强大的黑盒对手能够访问整个训练数据集 X0=XX_0 = XX0=X（注意这排除了用于评估攻击成功率的测试数据）。

为了构建合成网络，攻击者先验地选择一个替代架构 GGG，需要为其训练合成模型参数 θg\theta_gθg。攻击者使用已知的图像-标签对 DDD 和训练方法 MMM（例如 Adam $49$ ）来训练 θg\theta_gθg。在每次迭代中，使用以下数据增强技术将已知数据加倍：对于当前数据集 DDD 中的每个图像 xxx，对目标模型的黑盒访问给出标签 l=O(x)l = \mathcal{O}(x)l=O(x)。评估/计算合成网络分数向量 ggg 相对于其参数 θg\theta_gθg 在图像 xxx 上的 Jacobian 矩阵。将对应于类别标签 lll 的 Jacobian 矩阵列的正负号乘以一个（小）常数 λ\lambdaλ------这构成了一个向量，该向量被添加到 xxx 上。这为每个 xxx 生成一个新图像，从而使 DDD 加倍。经过 NNN 次迭代后，算法输出针对最终增强数据集 DDD 的训练参数 θg\theta_gθg。

E. 对抗样本生成

合成模型训练好后，需要从中创建对抗样本来攻击防御。因此，任何白盒攻击都可以在合成模型上运行以创建对抗样本。然后对手可以检查这个样本是否能愚弄防御。重申一下，在本文中我们关注黑盒对手，因此直接在防御上运行白盒攻击不在我们的对抗模型范围内。我们简要介绍以下我们用于对抗样本生成的常用白盒攻击：

快速梯度符号方法 (FGSM) -- $8$ ：计算 x′=x′+ϵ×sign(∇xL(x,l;θ))x' = x' + \epsilon \times sign(\nabla_x L(x, l; \theta))x′=x′+ϵ×sign(∇xL(x,l;θ))，其中 LLL 是模型 fff 的损失函数（例如，交叉熵）。

基本迭代方法 (BIM) -- $38$ ：xi′=clipx,ϵ(xi−1′+ϵr×sign(∇xi−1′L(xi−1′,l;θ))x'i = clip{x,\epsilon}(x'{i-1} + \frac{\epsilon}{r} \times sign(\nabla{x'{i-1}} L(x'{i-1}, l; \theta))xi′=clipx,ϵ(xi−1′+rϵ×sign(∇xi−1′L(xi−1′,l;θ))，其中 x0′=xx'_0 = xx0′=x，rrr 是迭代次数，clipclipclip 是裁剪操作。

卷 10, 2022

1469

===== 第 20 页 =====

K. Mahmood 等人：击败黑盒：用于对抗样本防御的屏障区
表 10. CIFAR-10 非目标混合黑盒攻击结果。注意 β\betaβ 列指的是所有非目标混合黑盒攻击中的最小鲁棒精度。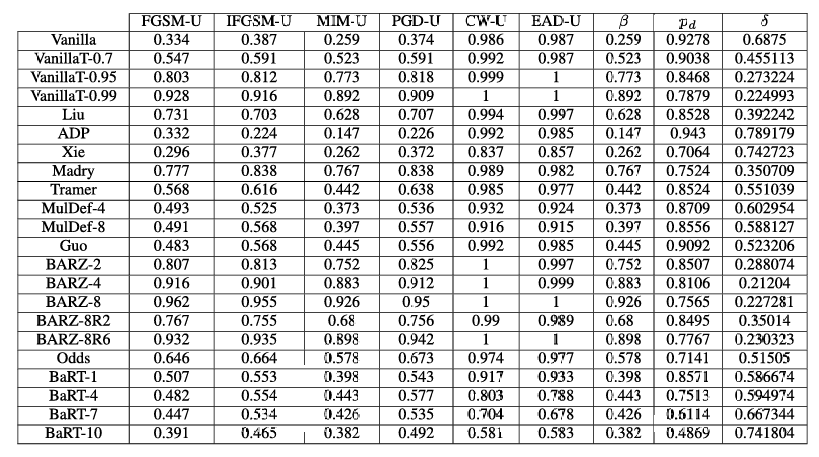

表 11. CIFAR-10 非目标纯黑盒攻击结果。注意 β\betaβ 列指的是所有非目标纯黑盒攻击中的最小鲁棒精度。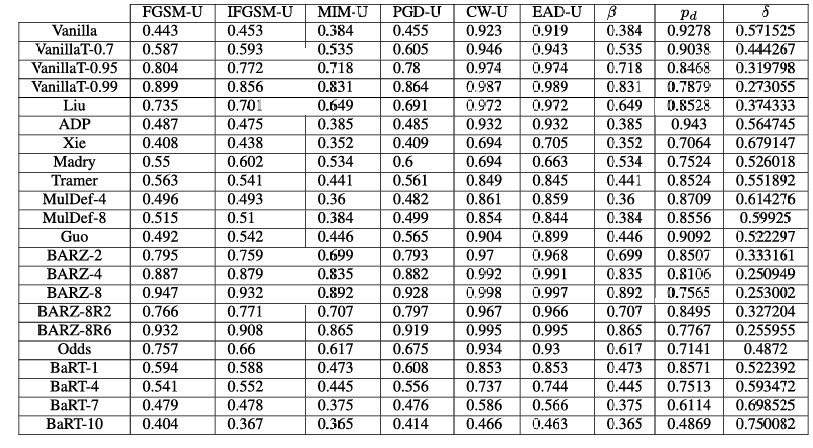

动量迭代方法 (MIM) -- $39$ ：这是 BIM 的一种变体，使用动量技巧创建梯度 gig_igi，即 xi′=clipx,ϵ(xi−1′+ϵ2×sign(gi))x_i' = \text{clip}{x, \epsilon} (x{i-1}' + \frac{\epsilon}{2} \times \text{sign}(g_i))xi′=clipx,ϵ(xi−1′+2ϵ×sign(gi))。

投影梯度下降 (PGD) -- $27$ ：这也是 BIM 的一种变体，其中裁剪操作被投影操作取代。

Carlini 和 Wagner 攻击 (C&W) -- $11$ ：我们定义 x′(ω)=12(tanh⁡ω+1)x'(\omega) = \frac{1}{2}(\tanh \omega + 1)x′(ω)=21(tanhω+1) 和 g(x)=max⁡(max⁡(si:i≠l)−si,−κ)g(x) = \max(\max(s_i : i \neq l) - s_i, -\kappa)g(x)=max(max(si:i=l)−si,−κ)，其中 f(x)=(s1,s2,...)f(x) = (s_1, s_2, \ldots)f(x)=(s1,s2,...) 是分类器 fff 对输入 xxx 的得分向量，κ\kappaκ 控制对抗样本的置信度。对手构建以下目标函数来寻找对抗性噪声。

min⁡ω∥x′(ω)−x∥22+cf(x′(ω)),\min_{\omega} \| x'(\omega) - x \|_2^2 + c f(x'(\omega)),minω∥x′(ω)−x∥22+cf(x′(ω)),

其中 ccc 是通过改进的二分搜索选择的常数。

弹性网络攻击 (EAD) -- $40$ ：这是 C&W 攻击的变体，具有以下目标函数。

min⁡ω∥x′(ω)−x∥22+β∥x′(ω)−x∥1+cf(x′(ω)).\min_{\omega} \| x'(\omega) - x \|_2^2 + \beta \| x'(\omega) - x \|_1 + c f(x'(\omega)).minω∥x′(ω)−x∥22+β∥x′(ω)−x∥1+cf(x′(ω)).

附录 D

实验实现细节与杂项

F. BARZ 的实现

在 BARZ 中，我们使用的图像变换由调整大小操作 i(x)i(x)i(x) 和线性变换 c(x)=Ax+bc(x) = Ax + bc(x)=Ax+b 组成。在 CNN 实现中，可以将 i(c(x))i(c(x))i(c(x)) 视为 CNN 架构本身中的一个额外层。我们将此额外层称为保护层。在 BARZ 中，保护层中的输入图像 xxx 被线性变换为图像 i(c(x))i(c(x))i(c(x))，然后才进入相应的 CNN 网络。

对于 BARZ 中每个保护层使用的调整大小操作 i(⋅)i(\cdot)i(⋅)，我们选择大于图像数据原始尺寸的尺寸。我们这样做是为了防止图像下采样造成的信息丢失（这会损害 BARZ 的干净精度）。在我们的实验中，我们使用具有 2、4 和 8 个保护层的 BARZ。每个保护层都有自己的调整大小操作 i(⋅)i(\cdot)i(⋅)。当使用 8 个保护层时，我们使用的图像调整大小操作是从 32 到 32、40、48、64、72、80、96、104。每个保护层将因每个层实现的调整大小程度不同而彼此区分。这将导致保护层之间的可迁移性降低，因此我们期望看到更宽的屏障区，从而降低攻击者的成功率。当使用 4 个保护层时，我们使用 BARZ 中 8 个网络对应于图像调整大小操作 32 到 32、48、72、96 的 4 个保护层副本。当使用 2 个保护层时，我们使用 BARZ 中 8 个网络对应于图像调整大小操作 32 到 32 和 104 的 2 个保护层副本。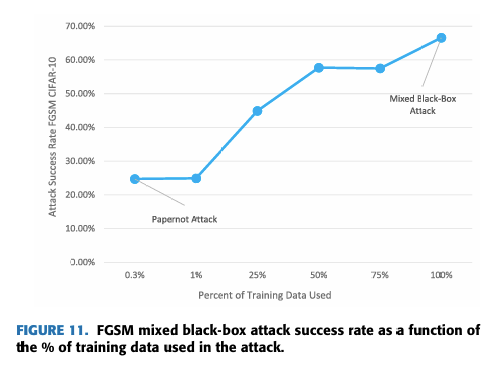

对于每个保护层，线性变换 c(x)=Ax+bc(x) = Ax + bc(x)=Ax+b 是从某个统计分布中随机选择的（该分布是公开知识，因此对手知道）。统计分布的设计取决于所考虑数据集的复杂性（在我们的案例中，我们使用 Fashion-MNIST 和 CIFAR-10 进行实验）。对于 CIFAR-10，我们将矩阵 AiA_iAi 视为单位矩阵（这也使得向量表示中的 AAA 成为单位矩阵），并且我们对每个矩阵 bib_ibi 使用相同的矩阵 bbb，即，

b′=b1=b2=b3.b' = b_1 = b_2 = b_3.b′=b1=b2=b3.

这意味着我们在像素的红、蓝、绿值上使用相同的随机偏移。做出这个设计决定的原因是，对于像 CIFAR-10 这样具有高空间复杂度的数据集，我们发现完全随机的 AAA 会导致干净精度大幅下降，即使网络被训练来学习这种失真。因此，对于像 CIFAR-10 这样的数据集，我们不随机选择 AAA。我们选择 AAA 为单位矩阵。同样，对于 b′b'b′，我们只随机生成 35% 的矩阵值，其余保留为 0。对于随机生成的值，我们从 -0.5 到 0.5 的均匀分布中选择它们。

===== 第 21 页 =====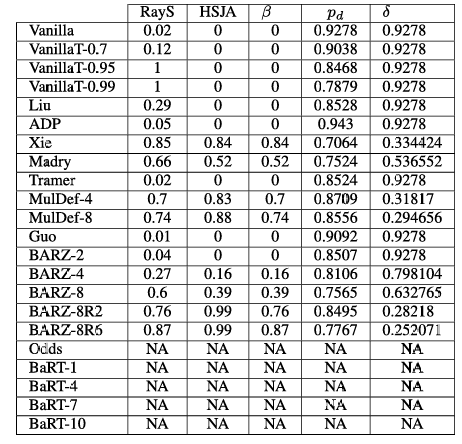

对于空间复杂度较低的数据集（如 Fashion-MNIST），我们令矩阵 A′=A1=A2=A3A' = A_1 = A_2 = A_3A′=A1=A2=A3 和 b′=b1=b2=b3b' = b_1 = b_2 = b_3b′=b1=b2=b3，并选择 A′A'A′ 和 b′b'b′ 为随机矩阵：A′A'A′ 和 b′b'b′ 的值选自均值为 μ=0\mu = 0μ=0、标准差为 σ=0.1\sigma = 0.1σ=0.1 的高斯分布。

G. 攻击和防御参数

为了实现黑盒攻击，我们首先运行算法 1 来训练合成网络 ggg。接下来，从测试数据（在我们的设置中每个数据集有 10,000 个样本）中，我们选择防御正确识别的前 1000 个样本。对于这 1000 个样本中的每一个，我们运行某种白盒攻击以生成 1000 个对抗样本。攻击成功率是这些样本中成功将 lll 改变为期望的新随机选择的 l′l'l′（目标攻击）或任何其他标签 l′≠⊥l' \neq \perpl′=⊥（非目标攻击）的比例。

结合我们的合成模型用于混合黑盒攻击和纯黑盒攻击的对抗生成技术（白盒攻击）的参数可以在表 13 中找到。对于除 Carlini 和 Wagner 攻击之外的所有攻击，我们使用 ∣∣l∣∣∞||l||_{\infty}∣∣l∣∣∞ 范数。对于 Carlini 和 Wagner 攻击，只有 ∣∣l∣∣2||l||2∣∣l∣∣2 实现（由作者提供）的运行时间效率足以满足我们当前的硬件设置（用于在 10 种防御和 2 个数据集上进行测试）。未来的工作可能包括在 Carlini 和 Wagner 攻击的高效 ∣∣l∣∣∞||l||{\infty}∣∣l∣∣∞ 实现可用时，尝试将其用于混合黑盒攻击。

表 14. 实验中使用的训练参数。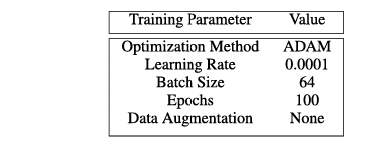

表 15. 混合黑盒攻击参数。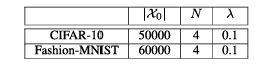

表 16. 来自 $11$ 的合成神经网络 ggg 的架构。

表 13. 攻击参数。 iii - 迭代次数, ddd - 衰减因子, rrr - 生成初始噪声的球半径, ccc - C&W 攻击的常数值, eee - 噪声幅度, β\betaβ - EAD 攻击的常数值。Binary Search = BL5r。

我们实验的精确设置在表 14、15 和 16 中给出。表 14 详述了算法 1 中的训练方法 TTT。对于评估的数据集 Fashion-MNIST 和 CIFAR-10（无数据增强），我们在表 15 中列出了训练数据量 ∣X0∣|X_0|∣X0∣ 以及参数 λ\lambdaλ 和 NNN（λ=0.1\lambda = 0.1λ=0.1 和 N=6N = 6N=6 取自基于预言机黑盒攻击的论文 $26$ ；注意大小为 10,000 的测试集是标准做法；所有剩余数据用于训练，攻击者可以完全访问）。

表 16 描述了不同数据集的合成网络 ggg 的 CNN 网络架构 GGG；该结构有几层（不要与 BARZ 中的"保护层"混淆，后者是一个图像变换加上整个 CNN）。对手试图攻击 BARZ，并将首先学习一个具有表 16 对应架构的合成模型 M(θ)M(\theta)M(θ)。请注意，图像变换是保密的，因此攻击者最多只能训练一个合成的普通网络。当然，攻击者确实知道 BARZ 中图像变换的选取范围，并且可能尝试为每个可能的图像变换学习一个合成 CNN，并对这些 CNN 输出的标签进行某种多数投票（像 BARZ 一样）。然而，存在指数级的变换，使得这种攻击不可行。

H. 边界攻击计算复杂性和目标边界攻击

在论文主体部分，我们提到 The Odds are Odd (Odds) 和随机变换轰炸 (BART) 都不适用于边界攻击。对于纯黑盒和混合黑盒攻击，我们可以使用 GPU 或多个 CPU 高效并行化许多样本的评估（在图像变换的情况下）。然而，边界攻击需要按顺序执行大量评估（例如每个样本 10,000 次查询），因此我们无法利用前面提到的并行性。这导致这些防御在我们标准实现下的边界攻击运行时间长达数周。这些攻击不适用于我们当前的设置（28 核 CPU 机器和 2 个 Titan V GPU）。

还值得注意的是，在本文中我们没有直接考虑目标边界攻击。虽然我们确实提供了其他一些黑盒目标攻击的实验细节，但本文我们主要关注非目标攻击。由于我们已经在本文中提出了 12 种目标攻击（6 种混合黑盒和 6 种纯黑盒类型），我们将目标边界攻击作为潜在的未来工作。

卷 10, 2022

1472

===== 第 22 页 =====

K. Mahmood 等人：击败黑盒：用于对抗样本防御的屏障区

IEEE Access

I. 未来工作

有几个有前景的方向可用于未来的工作。从安全角度来看，我们的论文已经证明了图像变换对于黑盒鲁棒性的有效性。我们实验了一组我们发现对创建屏障区有效的图像变换。然而，据我们所知，尚未对单一和固定组合图像变换的可迁移性进行大规模研究。精确确定哪些图像变换能够扭曲对抗性噪声同时保持鲁棒性，将使该领域更接近于建立一组图像变换作为安全原语。

在机器学习方面，通过引入新颖的架构，可能提高 BARZ 防御的干净精度。具体来说，大迁移模型 (Big Transfer Models) $50$ 是一类在 CIFAR-10 和 CIFAR-100 等数据集上表现出卓越性能的 CNN。使用这些新架构可能是提高 BARZ 防御干净精度的一种可能方式。

在攻击者方面，在这项工作中，我们只考虑对错误分类（目标或非目标）感兴趣的对手。攻击者从一个干净的样本开始，并特别试图避免样本被标记为正确标签或被标记为对抗性标签。据我们所知，对于这个问题的逆问题（即攻击者试图用被标记为对抗性的合法样本来淹没系统）尚未进行广泛研究。虽然这本身是一个有趣的问题，但它超出了我们当前工作的范围。这可能是未来的防御设计者想要考虑并尝试缓解的问题。

最后，在攻击者方面，自适应黑盒攻击仍然可以进行优化。在我们的论文中，我们通过实验发现了一种简单的 CNN 架构，它既易于训练，又能产生高度可迁移的对抗样本。然而，仍然有可能优化攻击中的架构，以潜在地提高攻击成功率。此外，随着白盒攻击的不断改进，有可能用更强的技术替代自适应黑盒攻击中的 MIM 对抗生成方法。

参考文献

$1$ A. Krizhevsky, I. Sutskever, and G. E. Hinton, "ImageNet classification with deep convolutional neural networks," in Proc. NIPS, F. Pereira, C. J. C. Burges, L. Bottou, and K. Q. Weinberger, Eds., 2012, pp. 1097-1105.

$2$ K. Simonyan and A. Zisserman, "Very deep convolutional networks for large-scale image recognition," in Proc. ICLR, 2015, pp. 1-14.

$3$ R. Girshick, "Fast R-CNN," in Proc. IEEE Int. Conf. Comput. Vis. (ICCV), Dec. 2015, pp. 1440-1448.

$4$ S. Ren, K. He, R. B. Girshick, and J. Sun, "Faster R-CNN: Towards real-time object detection with region proposal networks," in Proc. NIPS, 2015, pp. 91-99.

$5$ E. Shelhamer, J. Long, and T. Darrell, "Fully convolutional networks for semantic segmentation," IEEE Trans. Pattern Anal. Mach. Intell., vol. 39, no. 4, pp. 640-651, Apr. 2017.

$6$ J. Wang, Z. Zhang, C. Xie, Y. Zhou, V. Premachandran, J. Zhu, L. Xie, and A. Yuille, "Visual concepts and compositional voting," 2017, arXiv:1711.04451.

$7$ C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, I. Goodfellow, and R. Fergus, "Intriguing properties of neural networks," CoRR, vol. abs/1312.6199, 2013. $Online$ . Available: http://arxiv.org/abs/1312.6199

$8$ I. Goodfellow, J. Shlens, and C. Szegedy, "Explaining and harnessing adversarial examples," CoRR, vol. abs/1412.6572, 2014. $Online$ . Available: http://arxiv.org/abs/1412.6572

$9$ F. Tramer, N. Carlini, W. Brendel, and A. Madry, "On adaptive attacks to adversarial example defenses," 2020, arXiv:2002.08347.

$10$ A. Athalye, N. Carlini, and D. A. Wagner, "Orbitscated gradients give a false sense of security: Circumventing defenses to adversarial examples," in Proc. ICML, 2018, pp. 274-283.

$11$ N. Carlini and D. A. Wagner, "Adversarial examples are not easily detected: Bypassing ten detection methods," in Proc. ALSCOCCS, 2017, pp. 3-14.

$12$ N. Papernot, P. McDaniel, X. Wu, S. Jin, and A. Swami, "Distillation as a defense to adversarial perturbations against deep neural networks," in Proc. IEEE Symp. Secur. Privacy (SP), May 2016, pp. 582-597.

$13$ A. Kurakin, I. Goodfellow, and S. Bengio, "Adversarial machine learning at scale," CoRR, vol. abs/1611.01236, 2016. $Online$ . Available: http://arxiv.org/abs/1611.01236

$14$ F. Tramer, A. Kurakin, N. Papernot, I. Goodfellow, D. Boneh, and P. McDaniel, "Ensemble adversarial training: Attacks and defenses," in Proc. Int. Conf. Learn. Represent., 2018.

$15$ X. Cao and N. Z. Gong, "Mitigating evasion attacks to deep neural networks via region-based classification," in Proc. 33rd Annu. Comput. Secur. Appl. Conf., 2017, pp. 278-287.

$16$ J. H. Metzen, T. Genewein, V. Fischer, and B. Bischoff, "On detecting adversarial perturbations," CoRR, vol. abs/1702.04267, 2017. $Online$ . Available: http://arxiv.org/abs/1702.04267

$17$ R. Feinman, R. R. Curtin, S. Shintre, and A. B. Gardner, "Detecting adversarial samples from artifacts," 2017, arXiv:1703.00410.

$18$ C. Xie, J. Wang, Z. Zhang, Z. Ren, and A. Yuille, "Mitigating adversarial effects through randomization," in Proc. ICLR, 2018, pp. 1-16.

$19$ D. Meng and H. Chen, "MagNet: A two-pronged defense against adversarial examples," in Proc. ACM SIGSAC Conf. Comput. Commun. Secur., Oct. 2017, pp. 135-147.

$20$ C. Guo, M. Rana, M. Cisse, and L. van der Maaten, "Countering adversarial images using input transformations," in Proc. Int. Conf. Learn. Represent., 2018.

$21$ S. Srisakdee, Y. Zhang, Z. Zhong, W. Yang, T. Xie, and B. Li, "MULDEE: Multi-model-based defense against adversarial examples for neural networks," 2018, arXiv:1809.00065. (注：原文 MulDef 引文应为 $21$ )

$22$ E. Raff, J. Sylvester, S. Forsyth, and M. McLean, "Barrage of random transforms for adversarially robust defense," in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2019, pp. 6528-6537.

$23$ K. Roth, Y. Kilcher, and T. Hofmann, "The odds are odd: A statistical test for detecting adversarial examples," 2019, arXiv:1902.04818.

$24$ T. Pang, K. Xu, C. Du, N. Chen, and J. Zhu, "Improving adversarial robustness via promoting ensemble diversity," in Proc. ICML, 2019, pp. 4970-4979.

$25$ J. Chen, M. I. Jordan, and M. J. Wainwright, "HopSkipJumpAttack: A query-efficient decision-based attack," in Proc. IEEE Symp. Secur. Privacy (SP), May 2020, pp. 1277-1294.

$26$ N. Papernot, P. McDaniel, I. Goodfellow, S. Jha, Z. B. Celik, and A. Swami, "Practical black-box attacks against machine learning," in Proc. ACM Asia Conf. Comput. Commun. Secur., Apr. 2017, pp. 506-519.

$27$ A. Madry, A. Makelov, L. Schmidt, D. Tsipras, and A. Vladu, "Towards deep learning models resistant to adversarial attacks," in Proc. Int. Conf. Learn. Represent. (ICLR), 2018, pp. 1-28.

$28$ X. Yuan, P. He, Q. Zhu, and X. Li, "Adversarial examples: Attacks and defenses for deep learning," IEEE Trans. Neural Netw. Learn. Syst., vol. 30, no. 9, pp. 2805-2824, 2019.

$29$ I. Goodfellow, J. Shlens, and C. Szegedy, "Explaining and harnessing adversarial examples," in Proc. Int. Conf. Learn. Represent. (ICLR), 2015, pp. 1-11.

$30$ N. Carlini, A. Athalye, N. Papernot, W. Brendel, J. Rauber, D. Tsipras, I. Goodfellow, A. Madry, and A. Kurakin, "On evaluating adversarial robustness," 2019, arXiv:1902.06705.

$31$ C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, I. Goodfellow, and R. Fergus, "Intriguing properties of neural networks," in Proc. ICLR, 2014, pp. 1-10.

卷 10, 2022

1473

===== 第 23 页 =====

IEEE Access

K. Mahmood 等人：击败黑盒：用于对抗样本防御的屏障区

$32$ N. Papernot, P. McDaniel, and I. Goodfellow, "Transferability in machine learning: From phenomena to black-box attacks using adversarial samples," 2016, arXiv:1605.07277.

$33$ Y. Liu, X. Chen, C. Liu, and D. Song, "Delving into transferable adversarial examples and black-box attacks," in Proc. ICLR, 2017, pp. 1-24.

$34$ J. Chen and Q. Gu, "RayS: A ray searching method for hard-label adversarial attack," 2020, arXiv:2006.12792.

$35$ W. Brendel, J. Rauber, and M. Bethge, "Decision-based adversarial attacks: Reliable attacks against black-box machine learning models," 2017, arXiv:1712.04248.

$36$ P.-Y. Chen, H. Zhang, Y. Sharma, J. Yi, and C.-J. Hsieh, "ZOO: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models," in Proc. 10th ACM Workshop Artif. Intell. Secur., Nov. 2017, pp. 15-26.

$37$ C. Guo, J. R. Gardner, Y. You, A. G. Wilson, and K. Q. Weinberger, "Simple black-box adversarial attacks," 2019, arXiv:1905.07121.

$38$ A. Kurakin, I. Goodfellow, and S. Bengio, "Adversarial examples in the physical world," in Proc. Int. Conf. Learn. Represent. (ICLR) Workshop, 2017, pp. 1-14.

$39$ Y. Dong, F. Liao, T. Pang, H. Su, J. Zhu, X. Hu, and J. Li, "Boosting adversarial attacks with momentum," in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2018, pp. 9185-9193.

$40$ P.-Y. Chen, Y. Sharma, H. Zhang, J. Yi, and C.-J. Hsieh, "EAD: Elastic-net attacks to deep neural networks via adversarial examples," in Proc. 32nd AAAI Conf. Artif. Intell., 2018, pp. 1-8.

$41$ K. Mahmood, D. Gurevih, M. van Dijk, and P. Ha Nguyen, "Beware the black-box: On the robustness of recent defenses to adversarial examples," 2020, arXiv:2006.10876.

$42$ D. Tsipras, S. Samurkar, L. Engstrom, A. Turner, and A. Madry, "Robustness may be at odds with accuracy," in Proc. Int. Conf. Learn. Represent., 2019, pp. 1-24. $Online$ . Available: https://openreview.net/forum?id=SyxAb30cY7

$43$ H. Zhang, Y. Yu, J. Jiao, E. Xing, L. El Ghaoui, and M. Jordan, "Theoretically principled trade-off between robustness and accuracy," in Proc. Int. Conf. Mach. Learn., 2019, pp. 7472-7482.

$44$ H. Xiao, K. Rasul, and R. Vollgraf, "Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms," 2017, arXiv:1708.07747.

$45$ A. Krizhevsky, V. Nair, and G. Hinton, CIFAR-10 (Canadian Institute for Advanced Research). Accessed: Apr. 15, 2019. $Online$ . Available: http://www.cs.toronto.edu/\~kriz/cifar.html

$46$ K. He, X. Zhang, S. Ren, and J. Sun, "Deep residual learning for image recognition," in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2016, pp. 770-778.

$47$ K. Simonyan and A. Zisserman, "Very deep convolutional networks for large-scale image recognition," 2014, arXiv:1409.1556.

$48$ N. Carlini and D. Wagner, "Magnet and 'efficient defenses against adversarial attacks' are not robust to adversarial examples," 2017, arXiv:1711.08478.

$49$ D. P. Kingma and J. Ba, "Adam: A method for stochastic optimization," 2014, arXiv:1412.6980.

$50$ A. Kolesnikov, L. Beyer, X. Zhai, J. Puigcerver, J. Yung, S. Gelly, and N. Houlsby, "Big transfer (BIT): General visual representation learning," in Proc. Eur. Conf. Comput. Vis., in Lecture Notes in Computer Science, 2020, pp. 491-507, doi: 10.1007/978-3-030-58558-7_29.

作者简介

KALEEL MAHMOOD 分别于 2013 年、2016 年和 2017 年获得康涅狄格大学电气工程学士和硕士学位以及计算机科学硕士学位，目前正在该校攻读计算机科学博士学位。他的研究兴趣包括对抗性机器学习、深度学习、计算机视觉和安全性。

PHUONG HA NGUYEN 于 2008 年获得莫斯科国立罗蒙诺索夫大学计算机科学和数学专家学位，并于 2013 年获得南洋理工大学密码学博士学位。他目前在 eBay 担任研究员。他的研究兴趣包括机器学习和密码学。

LAM M. NGUYEN 于 2008 年获得莫斯科国立罗蒙诺索夫大学应用数学和计算机科学学士学位，2013 年获得麦克尼斯州立大学工商管理硕士学位，2018 年获得利哈伊大学工业与系统工程博士学位。他目前在 IBM 研究院托马斯·J·沃森研究中心担任研究科学家，研究领域为优化和机器学习。他当前的研究兴趣包括表示学习的优化、学习算法的设计与分析、深度强化学习和可解释人工智能。

THANH NGUYEN 于 2012 年获得河内科学技术大学计算机科学学士学位，并于 2020 年获得爱荷华州立大学计算机工程博士学位。他目前在亚马逊人工智能部门担任研究员。他的研究兴趣包括机器学习、学习理论、生成建模和无监督学习。

MARTEN VAN DIJK (IEEE 高级会员) 目前是荷兰国家数学与计算机科学研究院 (CWI) 计算机安全小组负责人，拥有超过 20 年的工业界（飞利浦研究院和 RSA 实验室）和学术界（麻省理工学院，并在 2020 年 6 月之前担任康涅狄格大学正教授，2020 年 6 月之后担任研究教授）经验。他的工作获得了 2015 年电子设计自动化领域的 A. Richard Newton 技术影响力奖，并获得了多项最佳（学生）论文奖。

卷 10, 2022

1474