PyTorch中神经网络的模型构建

要构建自定义模型，需完成两个核心步骤：继承 nn.Module 类；重载 init 方法（初始化）和 forward 方法（前向计算）

神经网络的构造

初始化方法（init）

def __init__(self, **kwargs):
    # 调用父类构造函数，确保Module的初始化逻辑被执行
    super(MLP, self).__init__(** kwargs)
    # 定义隐藏层：输入784维，输出256维
    self.hidden = nn.Linear(784, 256)
    # 定义激活函数
    self.act = nn.ReLU()
    # 定义输出层：输入256维，输出10维
    self.output = nn.Linear(256, 10)

super(MLP, self).init(**kwargs)这行代码非常重要，它会调用父类 Module 的构造函数，完成必要的初始化工作；self.hidden、self.act、self.output这些是我们定义的网络组件

**kwargs 是一个特殊的语法，用于在函数定义时接收任意数量的关键字参数（Keyword Arguments）。** 的作用是将参数收集为一个字典（dict），键为参数名，值为参数值。必须放在函数参数列表的末尾，否则会报错。

前向传播方法（forward）

def forward(self, x):
    o = self.act(self.hidden(x))  # 输入→隐藏层→激活函数
    return self.output(o)         # 激活结果→输出层

输入 x 首先通过隐藏层 self.hidden 进行线性变换；变换结果通过激活函数 self.act（ReLU）引入非线性特性；最后通过输出层 self.output 得到最终输出

我们只需要定义前向传播，反向传播会由 PyTorch 的自动求导机制自动生成

创建模型实例

net = MLP()  # 实例化MLP模型
print(net)   # 打印模型结构

输出：

MLP(
  (hidden): Linear(in_features=784, out_features=256, bias=True)
  (act): ReLU()
  (output): Linear(in_features=256, out_features=10, bias=True)
)

这表明我们的模型包含：

一个名为 hidden 的线性层（输入 784 维，输出 256 维）

一个 ReLU 激活函数层

一个名为 output 的线性层（输入 256 维，输出 10 维）

执行前向计算

X = torch.rand(2, 784)
output = net(X)  # 执行前向计算
print(output)

输出：

tensor([[ 0.0149, -0.2641, -0.0040,  0.0945, -0.1277, -0.0092,  0.0343,  0.0627,
         -0.1742,  0.1866],
        [ 0.0738, -0.1409,  0.0790,  0.0597, -0.1572,  0.0479, -0.0519,  0.0211,
         -0.1435,  0.1958]], grad_fn=<AddmmBackward>)

输出结果是一个形状为 (2, 10) 的张量，表示：2 个样本的输出，每个样本有 10 个输出值

这里并没有将 Module 类命名为 Layer (层)或者 Model (模型)之类的名字，这是因为该类是一个可供⾃由组建的部件。它的子类既可以是⼀个层(如PyTorch提供的 Linear 类)，⼜可以是一个模型(如这里定义的 MLP 类)，或者是模型的⼀个部分。

神经网络中常见的层

不含模型参数的层

import torch
from torch import nn

class MyLayer(nn.Module):
    def __init__(self, **kwargs):
        super(MyLayer, self).__init__(**kwargs)
    
    def forward(self, x):
        return x - x.mean()

# 测试
layer = MyLayer()
print(layer(torch.tensor([1, 2, 3, 4, 5], dtype=torch.float)))
# 输出: tensor([-2., -1.,  0.,  1.,  2.])

这个层不含模型参数，作用是把输入减去均值后输出

1. 无参数：不需要训练参数
2. 功能单一：通常执行固定的数学变换
3. 可复用：可以在多个模型中重复使用

含模型参数的自定义层

Parameter 类其实是 Tensor 的子类，如果一个 Tensor 是 Parameter ，那么它会⾃动被添加到模型的参数列表里。所以在⾃定义含模型参数的层时，我们应该将参数定义成 Parameter ，除了直接定义成 Parameter 类外，还可以使⽤ ParameterList 和 ParameterDict 分别定义参数的列表和字典。

使用 ParameterList 管理参数列表

与普通 Python 列表的关键区别在于，nn.ParameterList会通知 PyTorch 这些是需要优化的参数。

class MyListDense(nn.Module):
    def __init__(self):
        super(MyListDense, self).__init__()
        # 创建3个4x4的参数矩阵
        self.params = nn.ParameterList([
            nn.Parameter(torch.randn(4, 4)) for _ in range(3)
        ])
        # 添加一个4x1的参数矩阵
        self.params.append(nn.Parameter(torch.randn(4, 1)))

    def forward(self, x):
        for param in self.params:
            x = torch.mm(x, param)
        return x

# 测试
net = MyListDense()
print(net)

使用 ParameterDict 管理参数字典

ParameterDict 用于管理带键名的参数字典，适合需要根据条件选择不同参数的场景：

class MyDictDense(nn.Module):
    def __init__(self):
        super(MyDictDense, self).__init__()
        # 初始化参数字典
        self.params = nn.ParameterDict({
            'linear1': nn.Parameter(torch.randn(4, 4)),
            'linear2': nn.Parameter(torch.randn(4, 1))
        })
        # 添加新参数
        self.params.update({'linear3': nn.Parameter(torch.randn(4, 2))})

    def forward(self, x, choice='linear1'):
        return torch.mm(x, self.params[choice])

# 测试
net = MyDictDense()
print(net)
print(net(torch.randn(1, 4), 'linear2'))  # 使用指定参数进行前向计算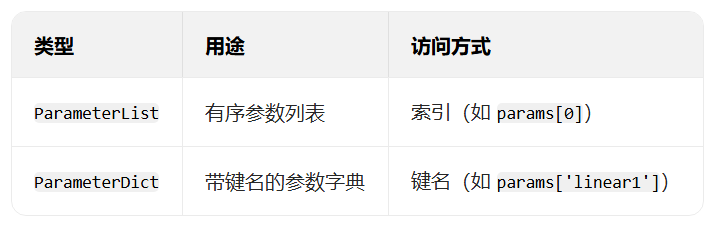

自定义二维卷积层

import torch
from torch import nn

# 卷积运算（二维互相关）
def corr2d(X, K):
    h, w = K.shape
    X, K = X.float(), K.float()
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
    return Y

# 二维卷积层
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super(Conv2D, self).__init__()
        # 初始化卷积核参数
        self.weight = nn.Parameter(torch.randn(kernel_size))
        # 初始化偏置参数
        self.bias = nn.Parameter(torch.randn(1))

    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

首先根据卷积核的大小确定输出特征图的尺寸，然后通过双重循环遍历输入的每个可能区域，在每个区域上执行元素级乘法并求和，得到对应位置的输出值。这个过程可以看作是使用一个小的矩阵（卷积核）在大矩阵（输入）上滑动，每次计算重叠区域的相似度。

自定义的 Conv2D 模块继承自 nn.Module，包含权重和偏置两个核心参数。权重参数表示卷积核，其形状由 kernel_size 参数指定，而偏置参数则为每个输出值添加一个可学习的常数。前向传播过程简单直接：调用 corr2d 函数执行卷积操作，然后添加偏置项。

卷积层的填充与步幅

保持输出尺寸与输入相同

这段代码展示了如何使用 PyTorch 的卷积层并通过填充 (padding) 操作保持输入输出尺寸相同。我们先看comp_conv2d辅助函数，它的作用是简化卷积操作的调用：将输入张量扩展为包含批量维度和通道维度的四维张量 (格式为[批量, 通道, 高度, 宽度])，然后通过卷积层计算输出，最后再移除批量和通道维度，返回二维的输出结果。

具体来看卷积层的定义：这里创建了一个nn.Conv2d实例，设置了输入通道数和输出通道数都为 1（处理单通道图像），卷积核大小为 3×3，并指定了两侧各填充 1 个像素。当卷积核在图像上滑动时，填充操作会在输入图像的边界周围添加额外的像素（默认填充值为 0），这样可以避免卷积操作导致的尺寸缩减。

在二维卷积操作中，输出尺寸的计算公式为：

输出高度 = (输入高度 + 2× 填充 - 卷积核高度) / 步长 + 1
输出宽度 = (输入宽度 + 2× 填充 - 卷积核宽度) / 步长 + 1

填充(padding)是指在输⼊高和宽的两侧填充元素(通常是0元素)。

例子中，参数设置如下：

• 输入尺寸：8×8
• 卷积核大小：3×3（高度 = 3，宽度 = 3）
• 填充（padding）：1（两侧各填充 1 个像素）
• 步长（stride）：默认值 1（代码中未显式指定）

当我们设置padding=1时，PyTorch 会在输入张量的上下左右各添加 1 行 / 列的零值像素。因此，实际参与卷积计算的输入尺寸变为：

原始高度 + 2×填充 = 8 + 2×1 = 10
原始宽度 + 2×填充 = 8 + 2×1 = 10

对于 3×3 的卷积核，在填充后的 10×10 输入上滑动时，其中心点可以到达的有效区域为：

• 垂直方向：从第 2 行（索引 1）到第 9 行（索引 8），共 8 个位置
• 水平方向：从第 2 列（索引 1）到第 9 列（索引 8），共 8 个位置

因此有：

输出高度 = (10 - 3) / 1 + 1 = 7 + 1 = 8 输出宽度 = (10 - 3) / 1 + 1 = 7 + 1 = 8

import torch
from torch import nn

# 辅助函数：计算卷积结果
def comp_conv2d(conv2d, X):
    X = X.view((1, 1) + X.shape)  # 添加批量和通道维度
    Y = conv2d(X)
    return Y.view(Y.shape[2:])  # 移除批量和通道维度

# 3x3卷积核，两侧各填充1
conv2d = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3, padding=1)

X = torch.rand(8, 8)  # 输入尺寸8x8
print(comp_conv2d(conv2d, X).shape)  # 输出尺寸仍为8x8

非对称填充与步幅

# 5x3卷积核，高度方向填充2，宽度方向填充1，步幅为(3, 4)
conv2d = nn.Conv2d(1, 1, kernel_size=(5, 3), padding=(2, 1), stride=(3, 4))
print(comp_conv2d(conv2d, X).shape)  # 输出尺寸: [2, 2]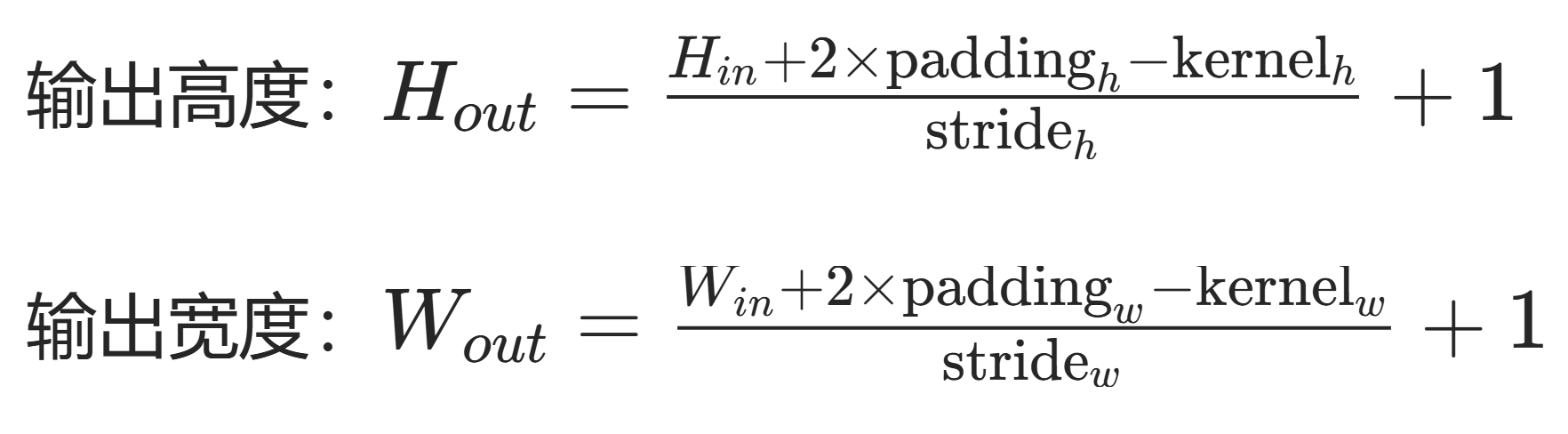

自定义池化层

池化层（Pooling Layer）是一种重要的下采样操作层，它的核心作用是通过对输入特征图的局部区域进行聚合计算，在减少特征图尺寸的同时保留关键信息。池化层就像一个 "信息筛选器"，它会滑动过输入的特征图，对每个局部区域提取一个代表性的值，让特征图变得更紧凑。

import torch
from torch import nn

def pool2d(X, pool_size, mode='max'):
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()  # 最大池化
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()  # 平均池化
    return Y

# 测试
X = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]], dtype=torch.float)
print(pool2d(X, (2, 2)))  # 最大池化结果
print(pool2d(X, (2, 2), 'avg'))  # 平均池化结果

pool2d函数模拟了池化操作的基本过程。它需要输入张量X、池化窗口大小pool_size，以及指定池化模式（最大池化或平均池化）。函数首先根据输入尺寸和池化窗口大小计算输出特征图的尺寸，输出高度为输入高度减去池化窗口高度再加 1，宽度同理，这和卷积操作中计算输出尺寸的逻辑类似，因为池化窗口也是通过滑动来覆盖输入的。然后通过两层循环遍历输出特征图的每个位置，对输入中对应池化窗口覆盖的局部区域进行聚合计算，得到输出特征图的每个元素。

**最大池化（Max Pooling）**是池化层中最常用的一种方式，它的计算逻辑是在每个池化窗口覆盖的局部区域内，选取数值最大的元素作为该区域的代表值。比如在测试用例中，输入X是一个 3×3 的张量[[0, 1, 2], [3, 4, 5], [6, 7, 8]]，使用 2×2 的池化窗口进行最大池化时，第一个窗口覆盖的区域是[[0, 1], [3, 4]]，其中最大的值是 4；第二个窗口覆盖[[1, 2], [4, 5]]，最大值是 5；第三个窗口覆盖[[3, 4], [6, 7]]，最大值是 7；第四个窗口覆盖[[4, 5], [7, 8]]，最大值是 8，所以输出的最大池化结果是[[4., 5.], [7., 8.]]。最大池化的优势在于能够突出局部区域中最显著的特征，比如图像中亮度最高的像素点，适合保留边缘、纹理等关键信息。

**平均池化（Average Pooling）**则是另一种常见的池化方式，它在每个池化窗口覆盖的局部区域内，计算所有元素的平均值作为该区域的代表值。同样以测试用例为例，2×2 池化窗口下，第一个窗口[[0, 1], [3, 4]]的平均值是(0+1+3+4)/4 = 2；第二个窗口[[1, 2], [4, 5]]的平均值是(1+2+4+5)/4 = 3；第三个窗口[[3, 4], [6, 7]]的平均值是(3+4+6+7)/4 = 5；第四个窗口[[4, 5], [7, 8]]的平均值是(4+5+7+8)/4 = 6，所以平均池化的输出结果是[[2., 3.], [5., 6.]]。平均池化的特点是能够平滑局部区域的特征，保留区域的整体趋势，避免个别极端值对特征的过度影响。

• 无参数：不需要训练参数
• 降维：减小特征图尺寸，降低计算复杂度
• 特征提取：保留主要特征，增强模型鲁棒性

模型示例

LeNet

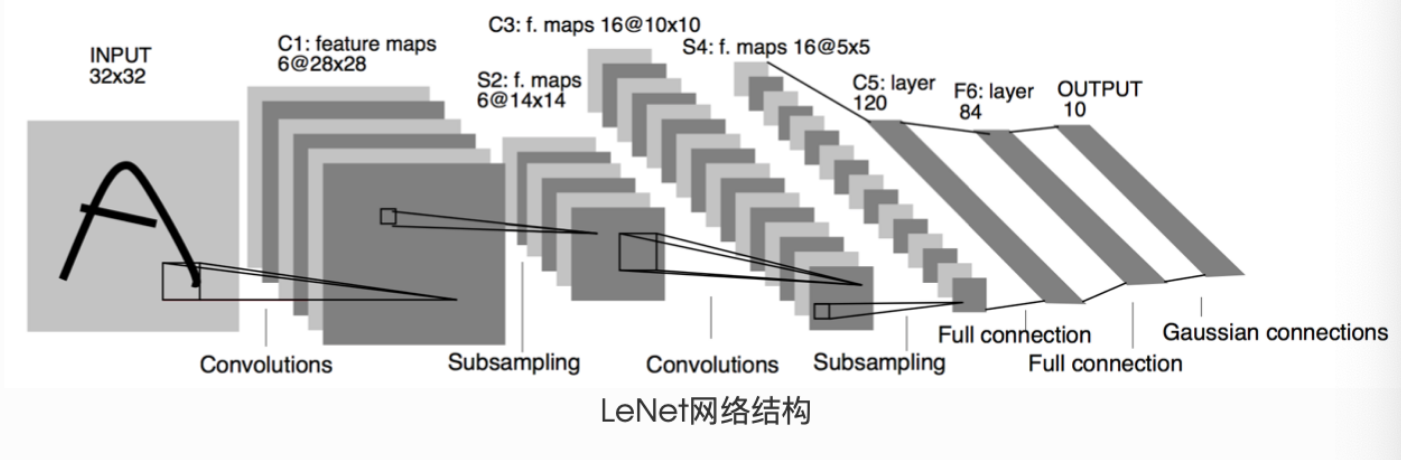
LeNet 是由深度学习先驱 Yann LeCun 于 1998 年提出的卷积神经网络，专门用于手写数字识别任务。作为早期卷积神经网络的经典代表，LeNet 展示了卷积操作在图像处理中的强大能力，为后续深度学习的发展奠定了重要基础。

LeNet 采用了卷积层 + 池化层 + 全连接层的经典组合结构，其核心思想是利用卷积操作提取图像局部特征，通过池化层降低特征维度，最后通过全连接层完成分类。标准 LeNet-5 结构包含 7 层（不含输入层），分为特征提取和分类两个部分：

• 特征提取部分：由 2 个卷积层和 2 个池化层交替组成
• 分类部分：由 3 个全连接层组成

一个神经网络的典型训练过程如下：

1. 定义包含一些可学习参数(或者叫权重）的神经网络

2. 在输入数据集上迭代

3. 通过网络处理输入

4. 计算 loss (输出和正确答案的距离）

5. 将梯度反向传播给网络的参数

6. 更新网络的权重，一般使用一个简单的规则：weight = weight - learning_rate * gradient

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))  # 第一个卷积层
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1)) # 第二个卷积层
  (fc1): Linear(in_features=400, out_features=120, bias=True) # 第一个全连接层
  (fc2): Linear(in_features=120, out_features=84, bias=True)  # 第二个全连接层
  (fc3): Linear(in_features=84, out_features=10, bias=True)   # 第三个全连接层
)

网络初始化（__init__ 方法）

import torch
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # 输入图像channel：1；输出channel：6；5x5卷积核
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # 全连接层：y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

• conv1：输入通道数 = 1（灰度图像），输出通道数 = 6，卷积核大小 = 5×5
• conv2：输入通道数 = 6（上一层输出），输出通道数 = 16，卷积核大小 = 5×5
• fc1：输入特征数 = 16×5×5（上一层输出展平后），输出特征数 = 120
• fc2：输入特征数 = 120，输出特征数 = 84
• fc3：输入特征数 = 84，输出特征数 = 10（对应 10 个类别）

前向传播（forward 方法）

def forward(self, x):
    # 第一层：卷积 → ReLU激活 → 2x2最大池化
    x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
    # 第二层：卷积 → ReLU激活 → 2x2最大池化（方阵可简化参数）
    x = F.max_pool2d(F.relu(self.conv2(x)), 2)
    # 展平特征图：将多维特征转为一维向量
    x = x.view(-1, self.num_flat_features(x))
    # 第三层：全连接 → ReLU激活
    x = F.relu(self.fc1(x))
    # 第四层：全连接 → ReLU激活
    x = F.relu(self.fc2(x))
    # 输出层：全连接（无激活函数，通常配合softmax使用）
    x = self.fc3(x)
    return x

输入图像                  [batch_size, 3, 224, 224]
↓ 第一层卷积+池化          [batch_size, 16, 112, 112]
↓ 第二层卷积+池化          [batch_size, 32, 56, 56]
↓ 展平                    [batch_size, 100352]
↓ 全连接层1               [batch_size, 1024]
↓ 全连接层2               [batch_size, 512]
↓ 输出层                  [batch_size, 10]

辅助函数：特征展平计算

def num_flat_features(self, x):
    size = x.size()[1:]  # 除去批处理维度的其他所有维度
    num_features = 1
    for s in size:
        num_features *= s
    return num_features

在卷积神经网络中，当我们从卷积层过渡到全连接层时，需要将多维的特征图（例如[batch_size, channels, height, width]）展平为一维向量。这个函数就是用来计算展平后的向量长度的。

LeNet 的参数与计算特性

params = list(net.parameters())
print(f"参数总数: {len(params)}")
print(f"conv1权重维度: {params[0].size()}")  # conv1的权重参数

输出：

参数总数: 10
conv1权重维度: torch.Size([6, 1, 5, 5])

每个卷积层包含：权重参数（out_channels × in_channels × kH × kW）+ 偏置参数（out_channels）

每个全连接层包含：权重参数（out_features × in_features）+ 偏置参数（out_features）

总参数计算：卷积层参数 + 全连接层参数 = 10 组参数（5 层 ×2 组参数 / 层）

前向传播测试

# 创建随机输入：batch_size=1，通道=1，高=32，宽=32
input = torch.randn(1, 1, 32, 32)
# 前向传播计算
out = net(input)
print(out)  # 输出10个类别的原始分数（logits）

输出：

tensor([[ 0.0672, -0.0743,  0.1058, -0.0181,  0.0536,  0.0736, -0.0764, -0.0423,
          0.0332, -0.0425]], grad_fn=<AddmmBackward>)

反向传播

# 清零所有参数的梯度缓存
net.zero_grad()
# 随机创建梯度张量，模拟反向传播
out.backward(torch.randn(1, 10))

torch.nn包对输入数据的处理要求 ------ 它只支持小批量（mini-batches）样本输入，不直接接受单个样本。这意味着无论是卷积层、全连接层还是其他网络层，输入张量都需要包含批量维度。例如nn.Conv2d要求输入是 4 维张量，形状为nSamples x nChannels x Height x Width，其中nSamples就是批量大小。如果只有单个样本，需要用input.unsqueeze(0)在第 0 维添加一个 "假的" 批量维度，把形状从nChannels x Height x Width变成1 x nChannels x Height x Width，这样才能被网络层正确处理。

AlexNet

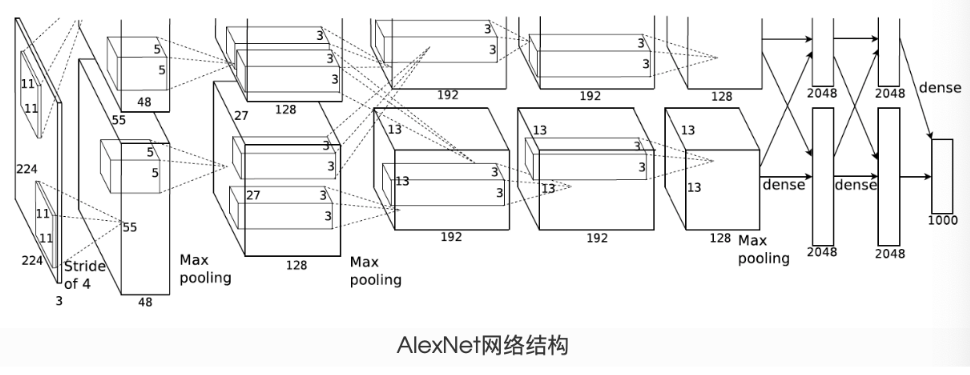
AlexNet 是由 Alex Krizhevsky、Ilya Sutskever 和 Geoffrey Hinton 在 2012 年提出的卷积神经网络，它在当年的 ImageNet 大规模视觉识别挑战赛 (ILSVRC) 中以显著优势夺冠，标志着深度学习在计算机视觉领域的突破性进展。AlexNet 的成功开启了深度学习的黄金时代，其架构设计理念深刻影响了后续神经网络的发展。

AlexNet 由 5 个卷积层和 3 个全连接层组成，总参数超过 6000 万个。网络结构分为两部分：

1. 特征提取部分：由卷积层和池化层构成，负责提取图像特征
2. 分类部分：由全连接层构成，负责基于提取的特征进行分类

层操作	输入维度	操作细节	输出维度
conv1	(1, 1, 224, 224)	11×11 卷积，步长 4，96 通道	(1, 96, 54, 54)
ReLU + 池化	(1, 96, 54, 54)	3×3 池化，步长 2	(1, 96, 26, 26)
conv2	(1, 96, 26, 26)	5×5 卷积，步长 1，填充 2，256 通道	(1, 256, 26, 26)
ReLU + 池化	(1, 256, 26, 26)	3×3 池化，步长 2	(1, 256, 12, 12)
conv3	(1, 256, 12, 12)	3×3 卷积，步长 1，填充 1，384 通道	(1, 384, 12, 12)
conv4	(1, 384, 12, 12)	3×3 卷积，步长 1，填充 1，384 通道	(1, 384, 12, 12)
conv5	(1, 384, 12, 12)	3×3 卷积，步长 1，填充 1，256 通道	(1, 256, 12, 12)
ReLU + 池化	(1, 256, 12, 12)	3×3 池化，步长 2	(1, 256, 5, 5)
展平	(1, 256, 5, 5)	多维转一维	(1, 6400)
fc1	(1, 6400)	全连接到 4096 维	(1, 4096)
fc2	(1, 4096)	全连接到 4096 维	(1, 4096)
fc3	(1, 4096)	全连接到 10 维	(1, 10)

特性	LeNet	AlexNet
网络深度	5 层（2 卷积 + 3 全连接）	8 层（5 卷积 + 3 全连接）
激活函数	Sigmoid/Tanh	ReLU
正则化	无	Dropout（丢弃率 0.5）
卷积核大小	5×5	11×11、5×5、3×3
通道数	6→16	96→256→384→384→256
全连接层维度	120→84→10	4096→4096→10
数据增强	无	有（随机裁剪、水平翻转等）
计算平台	CPU	GPU

参考文章

datawhalechina/thorough-pytorch: PyTorch入门教程，在线阅读地址：https://datawhalechina.github.io/thorough-pytorch/https://github.com/datawhalechina/thorough-pytorch