精准狙击：二叉树中的“左叶子”们与我的UI重构之旅（404. 左叶子之和）

精准狙击：二叉树中的"左叶子"们与我的UI重构之旅 😎

嘿，各位在代码的朋友们！我是你们的老朋友，一个热爱在代码中寻找规律与美的开发者。今天，我想和大家分享一个最近项目中遇到的"小麻烦"，以及我是如何从一道看似简单的算法题------LeetCode 404. 左叶子之和------中获得灵感，并漂亮地解决它的故事。这趟旅程充满了"踩坑"的教训和"恍然大悟"的喜悦，一起来看看吧！

我遇到了什么问题？

最近我接手了一个历史悠久的后台管理系统，其中有个核心功能是"动态配置页面"。这个页面的结构非常复杂，就像一棵巨大的树，每个节点代表一个配置项。有些配置项是最终的开关或输入框（我们称之为叶子节点 ），而有些则是一个配置组，下面还有更多的子配置项（非叶子节点）。

产品经理提了个新需求：为了界面清晰，希望所有配置组下的第一个 、且不可再展开的配置项，能有一个特殊的"推荐"高亮样式。

瞧，这不就是个典型的树操作问题嘛！"配置组"就是父节点，"第一个配置项"就是左孩子，"不可再展开"就是叶子节点。所以，我的任务抽象出来就是：找到这棵UI树里所有的"左叶子"节点，并对它们进行操作。作为第一步，我需要先统计一下这类节点的数量和它们的初始渲染耗时总和，来评估重构的影响。

于是，问题最终落到了这个算法题上：给定一个二叉树，求所有左叶子节点值的总和。

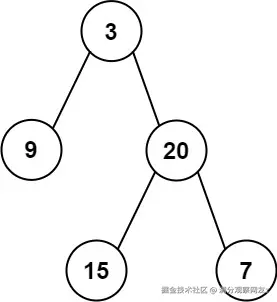
我是如何用"遍历"解决的

乍一看，这题不是挺简单的嘛？"不就是遍历一遍树，找到叶子节点，加起来就行了？"------如果你也这么想，恭喜你，你马上就要踩到我当初踩的第一个坑了！

踩坑与恍然大悟 😉

我最初的思路是这样的：写一个递归函数，如果当前节点是叶子节点，就返回它的值。

java 复制代码

// 错误示范 ❌
public int myWrongSum(TreeNode node) {
    if (node == null) return 0;
    // 只判断了自己是不是叶子！
    if (node.left == null && node.right == null) {
        return node.val;
    }
    // 然后递归左右子树
    return myWrongSum(node.left) + myWrongSum(node.right);
}

当我拿着这个逻辑去处理 [3,9,20,null,null,15,7] 这棵树时，我得到了 9 + 15 + 7 = 31，而不是预期的 24。我把右叶子7也给算进去了！

就在这时，我恍然大悟 ⚡️：一个节点是不是"左叶子"，它自己说了不算！必须由它的父节点来判定。就像你是不是"长子"，得问你爸妈，而不是问你自己。

这个小小的顿悟是解决本题的钥匙。我们判断的焦点，必须从"当前节点是什么"，转移到"当前节点的孩子是什么"。

有了这个核心思想，我立刻有了三种清晰的实现方案。

注意事项

因为题目中其实没有说清楚左叶子究竟是什么节点，左叶子的明确定义：一个节点的左孩子不为空，且左孩子左右孩子都为空（说明是叶子节点），那么该节点的左孩子为左叶子节点

解法一：深度优先搜索（DFS）- 递归版

这是最符合直觉的方案。我定义一个递归函数，在函数内部，我不关心当前节点 node 的身份，而是关心它的"左膀右臂"------node.left 和 node.right。

java 复制代码

/*
* 思路：深度优先搜索（DFS）递归。通过递归遍历树，在每个节点判断其"左孩子"是否为"左叶子"。
* 如果 node.left 存在且 node.left 没有子节点，就将其值加入结果。
* 然后递归地对左右子树求解，将三部分的结果相加。
* 时间复杂度：O(N)，因为每个节点都被访问一次。
* 空间复杂度：O(H)，H是树的高度。在最坏情况下（链状树），H=N，空间为O(N)；在最好情况下（完全二叉树），H=logN，空间为O(logN)。
*/
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) {
            return 0;
        }

        // --- 核心判断在此 ---
        // 在"我"这里，判断我的孩子。
        int midValue = 0;
        if (root.left != null && isLeaf(root.left)) {
            midValue = root.left.val;
        }

        // 递归地去问我的左孩子："你下面的左叶子和是多少？"
        int leftSum = sumOfLeftLeaves(root.left);
        // 同样地，问我的右孩子。
        int rightSum = sumOfLeftLeaves(root.right);
      
        return midValue + leftSum + rightSum;
    }
  
    // 这是一个辅助函数，清晰地定义了什么是"叶子节点"
    private boolean isLeaf(TreeNode node) {
        // 使用短路与&&，可以优雅地处理node为null的情况，避免空指针。
        return node != null && node.left == null && node.right == null;
    }
}

这个解法非常优雅，代码结构和我们的思考过程完全一致，完美！

时间复杂度：O(N)，其中 N 是树中节点的数量。因为深度优先搜索会访问树中的每一个节点恰好一次。
空间复杂度：O(H)，其中 H 是树的高度。这部分空间是递归调用栈所占用的。在最坏的情况下，树退化成一个链表，高度 H = N，空间复杂度为 O(N)。在树比较平衡的情况下，高度 H ≈ logN，空间复杂度为 O(logN)。

解法二：广度优先搜索（BFS）- 迭代版

递归虽好，但如果我的UI配置树特别深，就有可能造成"栈溢出"。为了程序的健壮性，我需要一个非递归的替代方案。这时候，使用队列的广度优先搜索（BFS）就登场了。

BFS像是在水面扔下一颗石子，波纹一圈圈地向外扩散，它能保证我们一层一层地访问节点。

java 复制代码

/*
* 思路：广度优先搜索（BFS）迭代。使用一个队列来存储待访问的节点，实现层序遍历。
* 每次从队列中取出一个节点，判断其左孩子是否为左叶子。如果是，累加其值。
* 然后，将其非空的左右孩子加入队列，以便继续遍历。
* 时间复杂度：O(N)，每个节点进出队列一次。
* 空间复杂度：O(W)，W是树的最大宽度。在最坏情况下（完全二叉树），W≈N/2，空间为O(N)。
*/
import java.util.Queue;
import java.util.LinkedList;

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) return 0;

        // Queue是接口，LinkedList是它的一个实现，提供了FIFO（先进先出）的功能，是BFS的标准配置。
        // 用offer()入队，poll()出队，是推荐的API，因为它们在队列满或空时不会抛出异常。
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
      
        int sum = 0;
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();

            // 同样的，在父节点node这里，判断它的左孩子。
            if (node.left != null && isLeaf(node.left)) {
                sum += node.left.val;
            }
          
            // 把孩子们加入队列，让"波纹"继续扩散
            if (node.left != null) queue.offer(node.left);
            if (node.right != null) queue.offer(node.right);
        }
      
        return sum;
    }
  
    // 辅助函数，保持代码清晰
    private boolean isLeaf(TreeNode node) {
        return node.left == null && node.right == null;
    }
}

BFS版本让我的代码库更加稳健，再也不怕遇到奇葩的"深度"配置了。

时间复杂度：O(N)。每个节点都会被入队一次、出队一次，所以每个节点上的操作是常数时间，总时间与节点数成正比。
空间复杂度：O(W)，其中 W 是树的最大宽度。空间开销主要来自队列，队列中最多存储一层节点。对于一个完美的二叉树，最后一层大约有 N/2 个节点，所以最坏情况下的空间复杂度是 O(N)。

解法三：深度优先搜索（DFS）- 迭代版

有时候，我们既想用DFS的遍历顺序，又想避免递归的风险。鱼和熊掌可以兼得吗？当然！我们可以用一个栈（Stack）来手动模拟递归过程。

java 复制代码

/*
* 思路：深度优先搜索（DFS）迭代。使用一个栈来模拟递归的调用过程。
* 每次从栈中弹出一个节点，检查其左孩子是否为左叶子。
* 为了模拟前序遍历的顺序（根-左-右），我们将右孩子先压栈，再压左孩子。
* 时间复杂度：O(N)，每个节点进出栈一次。
* 空间复杂度：O(H)，H是树的高度，与递归版本类似。最坏O(N)，最好O(logN)。
*/
import java.util.Stack;

class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if (root == null) return 0;

        // Stack是经典的后进先出（LIFO）数据结构，非常适合模拟DFS。
        // 现代Java更推荐使用ArrayDeque来实现栈，因为它通常性能更好。
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
      
        int sum = 0;
        while (!stack.isEmpty()) {
            // pop()会弹出栈顶元素。
            TreeNode node = stack.pop();

            if (node.left != null && isLeaf(node.left)) {
                sum += node.left.val;
            }
          
            // 注意这里的顺序！先右后左入栈。
            // 因为栈是后进先出，后压进去的左孩子会先被处理。
            if (node.right != null) stack.push(node.right);
            if (node.left != null) stack.push(node.left);
        }
      
        return sum;
    }

    private boolean isLeaf(TreeNode node) {
        return node.left == null && node.right == null;
    }
}

时间复杂度：O(N)。每个节点都会被入栈一次、出栈一次。
空间复杂度：O(H)，H 是树的高度。栈中存储的节点数量最多为树的高度。分析与递归DFS版本相同，最坏情况（链状树）为 O(N)，平衡情况下为 O(logN)。

举一反三，这个思想还能用在哪？

这个"一个节点的状态需要其父节点或上下文来决定"的思想，绝不仅仅局限于算法题，它就像一位可靠的向导，能引领我们穿越在日常开发的各种复杂场景中。一旦你掌握了它，你会发现很多问题都变得豁然开朗。

场景一：UI 渲染中的"位置魔法" ✨

在构建动态UI（无论是Web前端的React/Vue，还是移动端）时，组件的位置往往决定了它的样式和行为。

列表分割线 ：想象一个联系人列表，我们希望每个联系人下方都有分割线，但最后一个 除外。一个独立的联系人组件无法自己决定是否有分割线，它必须由渲染它的父列表来告知："嘿，你是最后一个，别画线了！" 父列表在遍历数据渲染子组件时，会检查当前索引是否为 list.length - 1，然后通过一个 prop（如 isLast={true}）将这个上下文信息传递下去。
智能圆角处理 ：在一个卡片组中，我们希望第一个卡片有顶部圆角，最后一个卡片有底部圆角。同样地，只有"卡片组"这个父容器知道谁是老大，谁是老幺。它会在渲染时为特定的子卡片添加特殊的CSS类，如 card-first 或 card-last。

这和我们解题时"在父节点判断其左孩子是否为左叶子"的思路是不是一模一样？都需要站在更高维度看待问题。

场景二：代码分析与AST的"语义探寻" 🔍

在编译器、Linter（如ESLint）或代码格式化工具（如Prettier）中，代码会被解析成一棵抽象语法树（AST）。对AST的分析，处处体现着"上下文决定论"。

变量作用域 ：要判断一个变量声明 let x; 是否未被使用，分析器不能只看这个声明节点。它必须扫描该声明所在的作用域（即AST中它的父级"块"节点及其所有后代），看看 x 是否被引用过。
Linter规则 ：ESLint有一条规则叫 no-lonely-if，禁止在else块中只包含一个if语句，建议合并为else if。当分析器访问到一个if语句节点时，为了应用此规则，它必须"回头看"，检查它的父节点是不是一个else块，并且这个else块是不是只有它一个孩子。没有父节点信息，这个规则根本无法实现。

场景三：文件系统与权限的"层层追溯" 📁

文件系统的组织结构本身就是一棵巨大的树。

构建绝对路径 ：一个文件对象本身通常只记录自己的名字，比如 report.docx。要得到它的完整路径 /Users/yourname/Documents/report.docx，你必须从当前节点出发，通过 parent 指针不断向上回溯，直到根目录 /，然后将路径拼接起来。每一步都需要父节点的信息。
权限继承：在类Unix系统中，你能否访问一个文件，不仅取决于该文件自身的读写权限，还取决于你是否拥有其所有上级目录的"执行"权限。要进行完整的权限检查，程序必须从文件节点开始，一路向上追溯到根目录，确保每一层"大门"都是敞开的。

从UI布局到编译器再到操作系统，这个看似简单的"依赖上下文"的思想无处不在。下次当你面对一个看似棘手的组件化或结构化问题时，不妨退后一步，从"父节点"的视角审视一下，也许答案就隐藏在这层关系之中。

类似好题推荐

如果你对树的遍历意犹未尽，可以试试这些题目，它们能极大地锻炼你对遍历的理解：

112. 路径总和：入门级的DFS，练习传递状态。
101. 对称二叉树：需要同时比较两个子树，对递归/迭代的理解要求更高。
102. 二叉树的层序遍历：BFS的教科书式应用。
226. 翻转二叉树：考察对树结构修改的理解，各种遍历都能做。

最终，通过这些清晰的思路，我不仅顺利完成了UI重构的数据评估，还对树的遍历有了更深刻的理解。一个小小的算法题，却能照亮我们解决实际工程问题的路，这也许就是我们热爱编程的原因吧！

三种解法对比

对比维度	解法1: 递归 DFS	解法2: 迭代 BFS (队列)	解法3: 迭代 DFS (栈)
核心思想	利用函数调用栈，自顶向下分解问题。	使用队列，一层一层地进行遍历。	使用显式的栈，手动模拟递归的深度优先过程。
实现复杂度	低。代码非常简洁，与人类思考方式高度一致。	中。需要手动管理队列和循环。	中。与BFS类似，但入栈顺序需要特别注意。
时间复杂度	`O(N)`，每个节点访问一次。	`O(N)`，每个节点进出队一次。	`O(N)`，每个节点进出栈一次。
空间复杂度	`O(H)`，H为树高 (最坏`O(N)`)，来自系统调用栈。	`O(W)`，W为树最大宽度 (最坏`O(N)`)，来自队列。	`O(H)`，H为树高 (最坏`O(N)`)，来自我们创建的栈。
优点	代码最直观，可读性最高。	绝对不会因树太深而栈溢出。	行为与递归一致，同时避免了栈溢出风险。
缺点	在树的深度非常大时，有栈溢出（Stack Overflow）的风险。	对于"瘦高"型的树，空间消耗可能比DFS小，但代码稍复杂。	相比递归，代码稍显繁琐，需要手动控制栈。