数据结构二叉树(2)---二叉树的实现

[1. 链式结构实现二叉树](#1. 链式结构实现二叉树)

[1.1 头文件---Tree.h](#1.1 头文件---Tree.h)

[1. 头文件保护宏](#1. 头文件保护宏)

[2. 包含标准库](#2. 包含标准库)

[3. 定义二叉树节点的数据类型](#3. 定义二叉树节点的数据类型)

[4. 定义二叉树节点的结构体](#4. 定义二叉树节点的结构体)

[5. 函数声明](#5. 函数声明)

[(1）遍历函数（前序、中序、后序）](#(1）遍历函数（前序、中序、后序）)

[(2）统计类函数](#(2）统计类函数)

[(3）查找与销毁函数](#(3）查找与销毁函数)

[6. 整体逻辑："声明 + 实现分离"](#6. 整体逻辑：“声明 + 实现分离”)

[1.2 实现文件---Tree.c](#1.2 实现文件---Tree.c)

[1. 遍历的思想](#1. 遍历的思想)

[2. 前序遍历函数---preOrder函数](#2. 前序遍历函数---preOrder函数)

[3. 中序遍历函数---inOrder函数](#3. 中序遍历函数---inOrder函数)

[4. 后序遍历函数---postOrder函数](#4. 后序遍历函数---postOrder函数)

[5. 统计二叉树结点个数函数---BinaryTreeSize函数](#5. 统计二叉树结点个数函数---BinaryTreeSize函数)

[6. 统计二叉树叶子节点个数---BinaryTreeLeafSize函数](#6. 统计二叉树叶子节点个数---BinaryTreeLeafSize函数)

[7. 二叉树第K层结点的个数函数---BinaryTreeLevelKSize函数](#7. 二叉树第K层结点的个数函数---BinaryTreeLevelKSize函数)

[8. 统计二叉树的深度/高度---BinaryTreeDepth函数](#8. 统计二叉树的深度/高度---BinaryTreeDepth函数)

[9. 二叉树查找值为x的结点函数---BinaryTreeFind函数](#9. 二叉树查找值为x的结点函数---BinaryTreeFind函数)

[10. ⼆叉树销毁函数---BinaryTreeDestory函数](#10. ⼆叉树销毁函数---BinaryTreeDestory函数)

[1.3 测试文件---test.c](#1.3 测试文件---test.c)

[1. 头文件与节点创建函数](#1. 头文件与节点创建函数)

[2. 二叉树创建函数 createBinaryTree()](#2. 二叉树创建函数 createBinaryTree())

[3. 测试函数 test01()](#3. 测试函数 test01())

[4. 主函数 main()](#4. 主函数 main())

[2. 总结:](#2. 总结:)

[2.1 头文件---Tree.h](#2.1 头文件---Tree.h)

[2.2 实现文件---Tree.c](#2.2 实现文件---Tree.c)

[2.3 测试文件---test.c](#2.3 测试文件---test.c)

在上篇内容中，小编主要讲了第二种实现树的方式------用链表结构实现的二叉树。通过结点的定

义，创建，树的构建三个方面介绍了链式二叉树。即如何"建树"而这篇文章小编主要围绕所建成的

树进行讲解，即如何"用树"。

为了容易理解，我们仍以上篇内容所建成的树进行讲解:

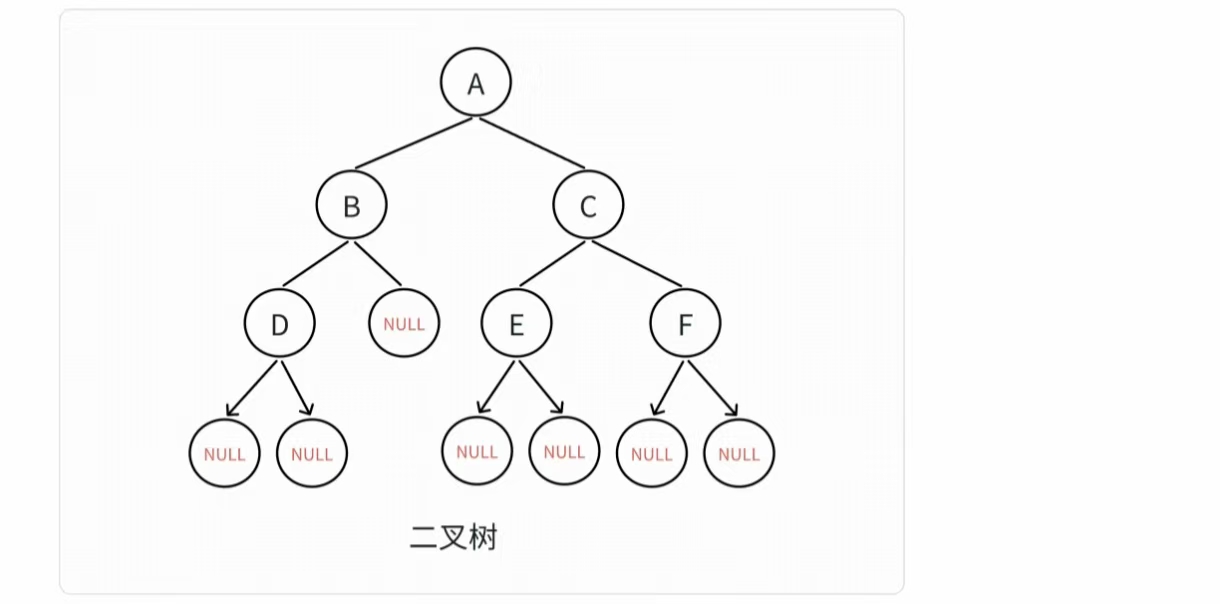
1. 链式结构实现二叉树

我们仍然用三个文件 : 头文件，实现文件和测试文件来进行封装。

1.1 头文件---Tree.h

cs 复制代码

#pragma once
#include<stdio.h>
#include<stdlib.h>

//定义链式结构的二叉树

typedef char BTDataType;
typedef struct BinaryTreeNode
{
    BTDataType data;
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
}BTNode;

//前序遍历
void preOrder(BTNode* root);
//中序遍历
void inOrder(BTNode* root);
//后序遍历
void postOrder(BTNode* root);


//二叉树结点个数
int BinaryTreeSize(BTNode* root);
//int BinaryTreeSize(BTNode* root,int* psize);

//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);

//二叉树第K层节点个数
int BinaryTreeLevelKSize(BTNode* root,int k);

////二叉树的深度/高度
int BinaryTreeDepth(BTNode* root);

//二叉树查找值为X的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);

//二叉树的销毁
void BinaryTreeDestory(BTNode** root);

以上时一个定义链式结构二叉树操作函数的头文件，包含二叉树的核心遍历、统计、查找及销毁等

功能声明。以下是各函数的详细解释及相互联系：

1. 头文件保护宏

(避免重复包含）

cs 复制代码

#pragma once

作用：这是编译器的"非标准但常用"语法，让头文件只被编译一次。
替代传统的 #ifndef ... #define ... #endif ，防止因头文件重复包含（比如多个 .c 文件都包含它）

导致的"重定义错误"。

2. 包含标准库

（为后续函数提供基础工具）

cs 复制代码

#include<stdio.h>   // 提供 printf 等输入输出函数（遍历打印时会用到）
#include<stdlib.h>  // 提供 malloc、free 等内存管理函数（二叉树销毁、创建时可能用到）

这两行是 C 语言标准库，后续写二叉树操作的 .c 实现文件时，若要打印遍历结果（用 printf ）、动态分配/释放节点（用 malloc / free ），就依赖这两个头文件。

3. 定义二叉树节点的数据类型

cs 复制代码

typedef char BTDataType;

含义：用 typedef 给 char 起别名 BTDataType ，统一管理二叉树节点存储的数据类型。
好处：如果后续想把节点数据改成 int / double 等，只需改这一行，不用满代码找 char 替换。

4. 定义二叉树节点的结构体

cs 复制代码

typedef struct BinaryTreeNode
{
    BTDataType data;                // 存储节点的值（类型是上面定义的 BTDataType，即 char）
    struct BinaryTreeNode* left;    // 指向左子树节点的指针（递归定义，因为子树也是 BinaryTreeNode 类型）
    struct BinaryTreeNode* right;   // 指向右子树节点的指针
}BTNode;

BTDataType data; ：存当前节点的数据（比如字符 'A' 、 'B' 等）。
struct BinaryTreeNode* left; ：指向左子节点的指针，若为 NULL 表示没有左子树。
struct BinaryTreeNode* right; ：指向右子节点的指针，若为 NULL 表示没有右子树。
typedef ... BTNode; ：给结构体 struct BinaryTreeNode 起别名 BTNode ，后续写代码时用

BTNode 更简洁。

5. 函数声明

(告诉编译器：这些函数"存在"，具体实现放 .c 文件）

(1）遍历函数（前序、中序、后序）

cs 复制代码

// 前序遍历：访问顺序 根 → 左子树 → 右子树
void preOrder(BTNode* root);  
// 中序遍历：访问顺序 左子树 → 根 → 右子树
void inOrder(BTNode* root);   

// 后序遍历：访问顺序 左子树 → 右子树 → 根
void postOrder(BTNode* root);

共同点：
参数都是 BTNode* root （传入二叉树的根节点指针，函数通过它递归访问整棵树）。
返回值 void （主要功能是"遍历并执行操作"，比如打印节点值，具体内容在实现文件里会写）。

(2）统计类函数

cs 复制代码

// 统计二叉树总节点数（所有节点，包括根、子节点）
int BinaryTreeSize(BTNode* root);  
// 统计二叉树叶子节点数（左右子树都为 NULL 的节点）
int BinaryTreeLeafSize(BTNode* root); 
// 统计二叉树第 k 层的节点数（根是第 1 层，以此类推）
int BinaryTreeLevelKSize(BTNode* root,int k); 
// 计算二叉树的深度（根到最远叶子节点的最大层数）
int BinaryTreeDepth(BTNode* root);

共同点：
都要"遍历/递归访问"二叉树节点，统计符合条件的节点数或层数。
返回值 int （结果是统计的数量或深度）。

(3）查找与销毁函数

cs 复制代码

// 在二叉树中查找值为 x 的节点，找到返回节点指针，没找到返回 NULL
BTNode* BinaryTreeFind(BTNode* root, BTDataType x); 
// 销毁二叉树（释放所有节点的内存，避免内存泄漏；二级指针是为了把 root 置 NULL）
void BinaryTreeDestory(BTNode** root);

特殊点：
BinaryTreeFind 返回 BTNode* （找到的节点地址），需遍历比较节点值。
BinaryTreeDestory 用二级指针 BTNode** root ：因为要在函数里把外部传入的根节点指针置

NULL （防止野指针），所以传指针的指针。

6. 整体逻辑："声明 + 实现分离"

头文件（ .h ）只做函数声明和数据类型定义，告诉编译器"有这些函数和结构"。
具体实现（ .c 文件）会写函数的实际代码（比如 preOrder 里递归访问并打印节点）。
这样设计是为了模块化：其他 .c 文件只需 #include "这个头文件" ，就能调用这些函数，不用关

心实现细节。

现在再看头文件，是不是每一行都清晰了？这些声明是后续写二叉树功能的"蓝图"，真正的逻辑在

对应的 .c 实现文件里。下面我们会在 .c文件中将这些函数一一介绍。

1.2 实现文件---Tree.c

上面内容我们讲解了链式结构实现二叉树的头文件，现在我们来讲讲实现文件，也就是其中各个函

数的实现。我们先从函数的遍历开始讲起。

首先，二叉树的操作离不开树的遍历，我们先来看看二叉树的遍历有哪些方式

按照规则，二叉树的遍历有：前序 / 中序 / 后序的递归结构遍历：

1. 前序遍历(Preorder Traversal 也称先序遍历)：访问根结点的操作发生在遍历其左右子树之前

访问顺序为：根结点、左子树、右子树

2. 中序遍历(Inorder Traversal)：访问根结点的操作发生在遍历其左右子树之中（间）

访问顺序为：左子树、根结点、右子树

3. 后序遍历(Postorder Traversal)：访问根结点的操作发生在遍历其左右子树之后

访问顺序为：左子树、右子树、根结点

1. 遍历的思想

二叉树遍历（前序、中序、后序）的核心思想，**本质是 "递归分解 + 回溯合并" ，**用更通用的方式

总结，包含这些关键逻辑：

核心思想：「分解问题 + 递归触底 + 回溯合并」

不管前序、中序、后序，遍历的本质都是把**"整棵树的遍历"拆解成"根 + 左子树 + 右子树"的子问**

题，通过递归深入到最底层（空节点），再回溯返回时按规则合并结果。可以拆成 3 步理解：

1. 分解问题：把大问题拆成子问题

二叉树的结构天然适合 "分治" ------ 任何一棵树，都能拆成 "根节点 + 左子树 + 右子树" 。遍历的目

标，就转化为：

先处理「根节点」（前序、中序、后序的区别，只在"什么时候处理根" ）
再递归处理「左子树」（子问题，和原问题逻辑完全一致）
最后递归处理「右子树」（子问题，和原问题逻辑完全一致）

2. 递归触底：用终止条件控制边界

**递归必须有 "终止条件" ，否则会无限循环。**二叉树遍历的终止条件很简单：

遇到 NULL （空节点）时，停止递归，直接返回。

这一步是让递归 "钻到最底层" 的关键 ------ 从根节点一路往左/右，直到触达空节点，才会开始

"往回走" 。

3. 回溯合并：从底层带着结果返回

当递归触达 NULL 后，会 "回溯" 到上一层调用的位置，继续执行 "未完成的逻辑" 。比如：

- 前序遍历中，访问完根节点 → 递归左子树触底返回 → 继续递归右子树

- 这个过程会把子树的遍历结果，合并成整棵树的遍历结果。

以前序（根 → 左 → 右）为例，"分解 + 递归 + 回溯" 的流程是：

分解：遍历整棵树 → 拆成 "访问 A（根） → 遍历左子树（B 为根的树） → 遍历右子树（C 为

根的树）"

递归触底：从 A→B→D，直到遇到 NULL ，触发终止条件返回
回溯合并：从 D 的 NULL 回溯到 D → 处理 D 的右子树（ NULL ）→ 回溯到 B → 处理 B 的右

子树（ NULL ）→ 回溯到 A → 处理 A 的右子树（C 为根的树）→ ...... 最终合并出完整序列

总结一下:

遍历的核心思想，就是 "用递归分解问题 → 靠终止条件控制边界 → 通过回溯合并结果" 。理解这

套逻辑，不管是二叉树的前/中/后序，还是更复杂的递归问题，都能找到思路～

下面我们来看代码的实现:

2. 前序遍历函数---preOrder函数
cs 复制代码
//前序遍历
void preOrder(BTNode* root)
{
    // 1. 递归终止条件：遇到空节点
    if (root == NULL)
    {
        printf("NULL "); 
        return;
    }
    // 2. 访问当前节点（根节点）
    printf("%c ", root->data); 
    // 3. 递归遍历左子树
    preOrder(root->left);     
    // 4. 递归遍历右子树
    preOrder(root->right);    
}
返回类型： void （无返回值，直接打印结果）

- 参数： BTNode* root （二叉树根节点指针）

核心逻辑：

若根节点为空，打印"NULL "并返回。

否则，先打印当前节点数据，再递归遍历左子树，最后递归遍历右子树（根→左→右）。

下面我们来举个例子

我们就用上篇文章建成的树为例:

就以前序遍历为例，按照根------左------右的步骤，我们在不看代码的情况下可以得出遍历结果为

A B D NULL NULL NULL C E NULL NULL F NULL NULL，下面我们根据代码来进行验

证:

第 1 层递归（处理根节点 A ）

cs 复制代码

void preOrder(BTNode* root)  // root = &A（非空）
{
    if (root == NULL) → 不成立，跳过
    printf("%c ", root->data); → 打印 "A "  
    preOrder(root->left);      → 调用 preOrder(&B)（进入第 2 层递归）
    // 注意：这里暂停，先执行完 preOrder(&B) 才会继续执行下面的 preOrder(&C)
}

当前输出： A

第 2 层递归（处理节点 B ）

cs 复制代码

void preOrder(BTNode* root)  // root = &B（非空）
{
    if (root == NULL) → 不成立，跳过
    printf("%c ", root->data); → 打印 "B "  
    preOrder(root->left);      → 调用 preOrder(&D)（进入第 3 层递归）
}

当前输出： A B

第 3 层递归（处理节点 D ）

cs 复制代码

void preOrder(BTNode* root)  // root = &D（非空）
{
    if (root == NULL) → 不成立，跳过
    printf("%c ", root->data); → 打印 "D "  
    preOrder(root->left);      → 调用 preOrder(NULL)（进入第 4 层递归）
}

当前输出： A B D

第 4 层递归（处理 D 的左孩子 NULL ）

cs 复制代码

void preOrder(BTNode* root)  // root = NULL（空节点）
{
    if (root == NULL) → 成立
    printf("NULL "); → 打印 "NULL "  
    return;          → 返回上一层（第 3 层）
}

当前输出： A B D NULL

回溯到第 3 层（继续处理 D 的右孩子）

第 3 层递归中， preOrder(root->left) 执行完，继续执行 preOrder(root->right) ：

cs 复制代码

void preOrder(BTNode* root)  // root = &D（回到这里）
{
    // 前面已执行：printf("D "); 和 preOrder(root->left);
    preOrder(root->right); → 调用 preOrder(NULL)（进入第 4 层递归）
}

第 4 层递归（处理 D 的右孩子 NULL ）

cs 复制代码

void preOrder(BTNode* root)  // root = NULL（空节点）
{
    if (root == NULL) → 成立
    printf("NULL "); → 打印 "NULL "  
    return;          → 返回上一层（第 3 层）
}

当前输出： A B D NULL NULL

回溯到第 2 层（继续处理 B 的右孩子）

第 2 层递归中， preOrder(root->left) 执行完，继续执行 preOrder(root->right) ：

cs 复制代码

void preOrder(BTNode* root)  // root = &B（回到这里）
{
    // 前面已执行：printf("B ");、preOrder(root->left);
    preOrder(root->right); → 调用 preOrder(NULL)（进入第 3 层递归）
}

第 3 层递归（处理 B 的右孩子 NULL ）

cs 复制代码

void preOrder(BTNode* root)  // root = NULL（空节点）
{
    if (root == NULL) → 成立
    printf("NULL "); → 打印 "NULL "  
    return;          → 返回上一层（第 2 层）
}

当前输出： A B D NULL NULL NULL

回溯到第 1 层（继续处理 A 的右孩子 C ）

第 1 层递归中， preOrder(root->left) 执行完，继续执行 preOrder(root->right) ：

cs 复制代码

void preOrder(BTNode* root)  // root = &A（回到这里）
{
    // 前面已执行：printf("A ");、preOrder(root->left);
    preOrder(root->right); → 调用 preOrder(&C)（进入第 2 层递归）
}

第 2 层递归（处理节点 C ）

cs 复制代码

void preOrder(BTNode* root)  // root = &C（非空）
{
    if (root == NULL) → 不成立，跳过
    printf("%c ", root->data); → 打印 "C "  
    preOrder(root->left);      → 调用 preOrder(&E)（进入第 3 层递归）
}

当前输出： A B D NULL NULL NULL C

第 3 层递归（处理节点 E ）

cs 复制代码

void preOrder(BTNode* root)  // root = &E（非空）
{
    if (root == NULL) → 不成立，跳过
    printf("%c ", root->data); → 打印 "E "  
    preOrder(root->left);      → 调用 preOrder(NULL)（进入第 4 层递归）
}

当前输出： A B D NULL NULL NULL C E

第 4 层递归（处理 E 的左孩子 NULL ）

cs 复制代码

void preOrder(BTNode* root)  // root = NULL（空节点）
{
    if (root == NULL) → 成立
    printf("NULL "); → 打印 "NULL "  
    return;          → 返回上一层（第 3 层）
}

当前输出： A B D NULL NULL NULL C E NULL

回溯到第 3 层（处理 E 的右孩子 NULL ）

cs 复制代码

void preOrder(BTNode* root)  // root = &E（回到这里）
{
    // 前面已执行：printf("E ");、preOrder(root->left);
    preOrder(root->right); → 调用 preOrder(NULL)（进入第 4 层递归）
}

第 4 层递归（处理 E 的右孩子 NULL ）

cs 复制代码

void preOrder(BTNode* root)  // root = NULL（空节点）
{
    if (root == NULL) → 成立
    printf("NULL "); → 打印 "NULL "  
    return;          → 返回上一层（第 3 层）
}

当前输出： A B D NULL NULL NULL C E NULL NULL

回溯到第 2 层（处理 C 的右孩子 F ）

第 2 层递归中， preOrder(root->left) 执行完，继续执行 preOrder(root->right) ：

cs 复制代码

void preOrder(BTNode* root)  // root = &C（回到这里）
{
    // 前面已执行：printf("C ");、preOrder(root->left);
    preOrder(root->right); → 调用 preOrder(&F)（进入第 3 层递归）
}

第 3 层递归（处理节点 F ）

cs 复制代码

void preOrder(BTNode* root)  // root = &F（非空）
{
    if (root == NULL) → 不成立，跳过
    printf("%c ", root->data); → 打印 "F "  
    preOrder(root->left);      → 调用 preOrder(NULL)（进入第 4 层递归）
}

当前输出： A B D NULL NULL NULL C E NULL NULL F

第 4 层递归（处理 F 的左孩子 NULL ）

cs 复制代码

void preOrder(BTNode* root)  // root = NULL（空节点）
{
    if (root == NULL) → 成立
    printf("NULL "); → 打印 "NULL "  
    return;          → 返回上一层（第 3 层）
}

当前输出： A B D NULL NULL NULL C E NULL NULL F NULL

回溯到第 3 层（处理 F 的右孩子 NULL ）

cs 复制代码

void preOrder(BTNode* root)  // root = &F（回到这里）
{
    // 前面已执行：printf("F ");、preOrder(root->left);
    preOrder(root->right); → 调用 preOrder(NULL)（进入第 4 层递归）
}

第 4 层递归（处理 F 的右孩子 NULL ）

cs 复制代码

void preOrder(BTNode* root)  // root = NULL（空节点）
{
    if (root == NULL) → 成立
    printf("NULL "); → 打印 "NULL "  
    return;          → 返回上一层（第 3 层）
}

当前输出： A B D NULL NULL NULL C E NULL NULL F NULL NULL

最终回溯到第 1 层，递归全部结束

此时第 1 层的 preOrder(root->right) （处理 C ）执行完毕，整个 preOrder(&A) 调用结束。

最终输出结果 : 按照前序遍历"根 → 左 → 右" 的顺序，最终打印结果为：

A B D NULL NULL NULL C E NULL NULL F NULL NULL

和我们开始的预测一样。

我们再来看一下对应逻辑：

cs 复制代码

1. 根节点  A  → 打印  A 
2.  A  的左子树（ B  为根）：
- 根  B  → 打印  B 
-  B  的左子树（ D  为根）：
- 根  D  → 打印  D 
-  D  的左子树（ NULL ）→ 打印  NULL 
-  D  的右子树（ NULL ）→ 打印  NULL 
-  B  的右子树（ NULL ）→ 打印  NULL 
3.  A  的右子树（ C  为根）：
- 根  C  → 打印  C 
-  C  的左子树（ E  为根）：
- 根  E  → 打印  E 
-  E  的左子树（ NULL ）→ 打印  NULL 
-  E  的右子树（ NULL ）→ 打印  NULL 
-  C  的右子树（ F  为根）：
- 根  F  → 打印  F 
-  F  的左子树（ NULL ）→ 打印  NULL 
-  F  的右子树（ NULL ）→ 打印  NULL

递归顺序：永远先处理"当前节点"，再递归左、递归右（前序本质）。
空节点处理：遇到 NULL 会打印 NULL ，保证遍历完整。
回溯过程：递归到最底层（空节点）后，会一层一层"回溯"，继续处理父节点的右子树。

这样逐行跟踪后，就能彻底理解前序遍历的递归流程，以及代码每一行在真实二叉树中是如何执

行的。

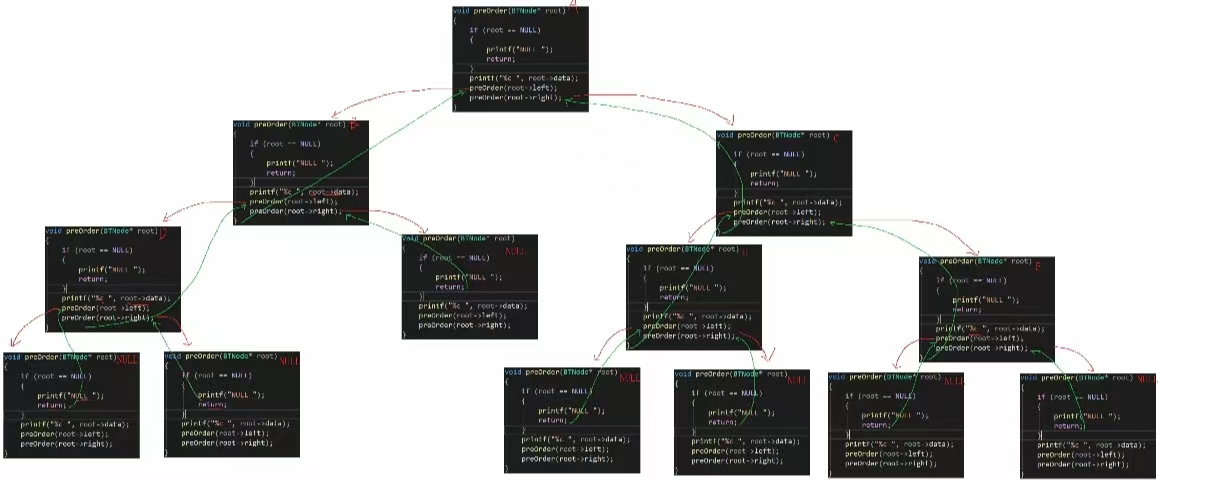
上面图片便是整个遍历递归流程图。可以看出来还是比较复杂的。再来看中序遍历:

3. 中序遍历函数---inOrder函数
cs 复制代码
//中序遍历
void inOrder(BTNode* root)
{
    if (root == NULL)
    {
    // 1. 递归终止条件：遇到空节点
        printf("NULL ");
        return;
    }
    // 2. 先递归遍历左子树
    inOrder(root->left);
    // 3. 访问当前节点（根节点）
    printf("%c ", root->data);
    // 4. 再递归遍历右子树
    inOrder(root->right);
}
返回类型： void

参数： BTNode* root （二叉树根节点指针）

核心逻辑：

若根节点为空，打印"NULL "并返回。

否则，先递归遍历左子树，再打印当前节点数据，最后递归遍历右子树（左→根→右）。

核心逻辑（一句话总结）

先递归遍历左子树，再访问当前节点，最后递归遍历右子树，空节点打印 NULL 。

我们再简单看一下流程。

中序遍历的规则是先遍历左子树，再访问当前节点，最后遍历右子树。下面一步一步走：

cs 复制代码

1. 从根 A 开始，先钻左子树（B分支） 
- 因为中序是"左→根→右"，所以碰到 A 后，不着急打印 A ，先去遍历 A 的左子树（B 那一支 ）。
2. 到 B 后，继续钻左子树（D分支）
- 到 B 这一层，同样不着急打印 B ，按照"左→根→右"，先去遍历 B 的左子树（D 那一支 ）。
3. 到 D 后，钻左子树（碰到 NULL）
- 到 D 这一层，还是先钻左子树 → 发现左子树是 NULL（空的 ）。
- 因为碰到空，触发"边界条件"，打印 NULL ，然后返回（回到 D 这一层 ）。
4. 打印 D，再钻 D 的右子树（碰到 NULL）
- 回到 D 后，按照"左→根→右"，左子树走完了，该打印 D 自己了 → 打印 D 。
- 打印完 D ，接着钻 D 的右子树 → 发现也是 NULL → 打印 NULL ，返回（回到 B 这一层 ）。
5. 打印 B，再钻 B 的右子树（碰到 NULL）
- 回到 B 后，左子树（D 分支）走完了，该打印 B 自己了 → 打印 B 。
- 打印完 B ，钻 B 的右子树 → 发现是 NULL → 打印 NULL ，返回（回到 A 这一层 ）。
6. 打印 A，再钻 A 的右子树（C 分支）
- 回到 A 后，左子树（B 分支）走完了，该打印 A 自己了 → 打印 A 。
- 打印完 A ，按照"左→根→右"，钻 A 的右子树（C 那一支 ）。
7. 到 C 后，钻左子树（E 分支）
- 到 C 这一层，不着急打印 C，先钻左子树（E 那一支 ）。
8. 到 E 后，钻左子树（碰到 NULL）
- 到 E 这一层，先钻左子树 → 发现是 NULL → 打印 NULL ，返回（回到 E 这一层 ）。
9. 打印 E，再钻 E 的右子树（碰到 NULL）
- 回到 E 后，左子树走完了，打印 E 自己 → 打印 E 。
- 打印完 E ，钻右子树 → 发现是 NULL → 打印 NULL ，返回（回到 C 这一层 ）。
10. 打印 C，再钻 C 的右子树（F 分支）
- 回到 C 后，左子树（E 分支）走完了，打印 C 自己 → 打印 C 。
- 打印完  C  ，钻右子树（ F  那一支 ）。
11. 到 F 后，钻左子树（碰到 NULL）
- 到 F 这一层，先钻左子树 → 发现是 NULL → 打印 NULL ，返回（回到 F 这一层 ）。
12. 打印 F，再钻 F 的右子树（碰到 NULL）
- 回到 F 后，左子树走完了，打印 F 自己 → 打印 F 。
- 打印完 F ，钻右子树 → 发现是 NULL → 打印 NULL ，返回（回到 C 这一层 ）。
13. 所有分支走完，遍历结束
- 回到 C 后，右子树（F 分支）走完了 → 整个 C 分支遍历结束。
- 回到 A 后，右子树（C 分支）也走完了 → 整个二叉树的中序遍历结束！

最终打印顺序把上面步骤里打印的内容按顺序连起来，结果是：

NULL D NULL B NULL A NULL E NULL C NULL F NULL

对应规则就是左子树 → 当前节点 → 右子树，碰到空节点就打印 NULL ，完美体现中序遍历的

逻辑。

4. 后序遍历函数---postOrder函数
cs 复制代码
//后序遍历
void postOrder(BTNode* root)
{
    if (root == NULL)
    {
    // 1. 递归终止条件：遇到空节点
        printf("NULL ");
        return;
    }
    // 2. 先递归遍历左子树
    postOrder(root->left);
    // 3. 再递归遍历右子树
    postOrder(root->right);
    // 3. 打印当前节点
    printf("%c ", root->data);
}
返回类型： void

参数： BTNode* root（二叉树根节点指针）

核心逻辑：

若根节点为空，打印"NULL "并返回。

否则，先递归遍历左子树，再递归遍历右子树，最后打印当前节点数据（左→右→根）。

最终后序遍历结果:

NULL NULL D NULL B NULL NULL E NULL NULL F C A

对应规则就是左子树 → 右子树 → 当前节点，碰到空节点打印 NULL 。

5. 统计二叉树结点个数函数---BinaryTreeSize函数
cs 复制代码
//二叉树结点个数
//法一:
//int size = 0;
//int BinaryTreeSize(BTNode* root)
//{
//    if (root == NULL)
//    {
//        return 0;
//    }
//    //结点非空, +1
//    size++;
//    BinaryTreeSize(root->left);
//    BinaryTreeSize(root->right);
//
//    return size;
//}
////法二:
//int BinaryTreeSize(BTNode* root, int* psize)
//{
//    if (root == NULL)
//    {
//        return 0;
//    }
//    //结点非空
//    (*psize)++;
//    BinaryTreeSize(root->left);
//    BinaryTreeSize(root->right);
//
//    return psize;
//}
//法三:
int BinaryTreeSize(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    return 1+ BinaryTreeSize(root->left)+BinaryTreeSize(root->right);
}
这三个函数都是用于计算二叉树节点个数的实现，核心目标一致，但思路和优缺点不同，以

下分别说明：

法一：全局变量计数

核心逻辑：

定义一个全局变量 size ，遍历二叉树时，每遇到一个非空节点就给 size 加 1，最后返回

size 。

流程：

从根节点开始，若节点非空则 size++ ，再递归遍历左、右子树，直到所有节点遍历完，size

就是总结点个数。

缺点：

全局变量 size 会一直存在，多次调用函数时需要手动重置，否则结果会累加（比如第一次

算完一棵树，第二次算另一棵树时， size 会从上次的结果继续增加），不够灵活。
法二：指针传递计数

核心逻辑：

通过指针参数 int* psize 传递一个计数器，遍历到非空节点时，通过指针修改计数器的值

（ (*psize)++ ）。

流程：

调用前需手动初始化一个计数器（如 int size = 0 ），传入指针 &size ，遍历过程中每遇到

非空节点就给 *psize 加 1，最终 size 的值就是总节点数。

注意：

代码中 return psize 是错误的（返回类型应为 int ，但 psize 是指针），实际应无需返回

值（ void ），或返回 *psize 。

优点：

解决了全局变量的问题，每次调用可通过新的计数器单独计算，但需要手动初始化计数器，

稍显繁琐。
法三：递归累加（最优实现）

核心逻辑：

利用递归的"分治思想"，一棵二叉树的节点数 = 1（当前节点） + 左子树节点数 + 右子树节

点数。

流程：

若节点为空，返回 0（空树节点数为 0）。

若节点非空，返回 1 + 左子树节点数（递归计算） + 右子树节点数（递归计算）。

优点：

无需全局变量或额外参数，纯递归实现，调用简单（直接传根节点即可），结果准确且无副

作用，是最推荐的写法。

总结:

三个方法都能计算节点数，但法三最简洁、安全，无需额外处理计数器，完全通过递归的"自下而

上累加"得到结果，是二叉树节点计数的标准实现。

6. 统计二叉树叶子节点个数---BinaryTreeLeafSize函数
cs 复制代码
int BinaryTreeLeafSize(BTNode* root)
{
    // 1. 空节点：没有叶子节点，返回 0
    if (root == NULL)
    {
        return 0;
    }
    // 2. 左右孩子都为空：当前节点是叶子节点，返回 1
    if (root->left == NULL && root->right == NULL)
    {
        return 1;
    }
    // 3. 非叶子节点：递归统计左、右子树的叶子数，相加后返回
    return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
这个函数用于统计二叉树中叶子节点（即左右孩子都为空的节点）的个数，核心逻辑是通过

递归分，逐层判断并累加叶子节点数量。

核心逻辑:

叶子节点的定义是"左右孩子都为空的节点"，函数通过递归遍历整棵树，对每个节点做两种

判断：

若节点为空，返回 0（空树没有叶子节点）。

若节点的左右孩子都为空，说明它是叶子节点，返回 1。

否则，当前节点不是叶子节点，递归统计它的左子树和右子树的叶子节点数，两者相加即为

当前节点所在树的叶子总数。

结合示例二叉树的执行流程、以先前的二叉树为例:

cs 复制代码

1. 从根 A 开始：
A 的左右孩子（B、C）都非空，所以不是叶子节点。递归计算左子树（B 分支）和右子树
(C 分支）的叶子数，再相加。
2. 处理 B 分支：
B 的左孩子是 D，右孩子是 NULL → 不是叶子节点。递归计算 B 的左子树( D 分支）的叶子
数（右子树为 NULL，返回0）。
D 的左右孩子都是 NULL → 是叶子节点，返回1。
因此，B 分支的叶子数 = 1（D）+ 0（B的右子树）= 1。
3. 处理 C 分支：
C 的左右孩子( E 、 F ）都非空 → 不是叶子节点。递归计算 C 的左子树（E 分支）和右子树
(F 分支）的叶子数。
- E 的左右孩子都是 NULL → 是叶子节点，返回 1。
- F 的左右孩子都是 NULL → 是叶子节点，返回 1。
因此，C 分支的叶子数 = 1（E）+ 1（F）= 2。
4. 总叶子数：
根 A 的叶子数 = B 分支（1）+ C 分支（2）= 3，与实际叶子节点（D 、E 、F）数量一致。

总结:

函数通过递归将"整棵树的叶子数"拆解为"左子树叶子数 + 右子树叶子数"，对每个节点仅判断"是否

为叶子"，逻辑清晰且无冗余，时间复杂度为 O(n) （每个节点访问一次），是统计二叉树叶子节

点的高效实现。

7. 二叉树第K层结点的个数函数---BinaryTreeLevelKSize函数
cs 复制代码
int BinaryTreeLevelKSize(BTNode* root, int k)
{
    // 1. 空树：第 k 层无节点，返回 0
    if (root == NULL)
    {
        return 0;
    }
    // 2. 已到第 k 层（k=1）：当前节点是第 k 层的，返回 1
    if (k == 1)
    {
        return 1;
    }
    // 3. 未到第 k 层：递归计算左、右子树的第 k-1 层节点数，相加后返回
    return BinaryTreeLevelKSize(root->left, k-1) + BinaryTreeLevelKSize(root->right, k-1);
}
这个函数用于计算二叉树中第 k 层节点的个数（根节点所在层为第 1 层），核心逻辑是通过

递归"逐层递减 k 值"，最终定位到第 k 层并统计节点数量。以下详细说明：

核心逻辑:

若树为空（ root == NULL ），第 k 层节点数为 0。

若 k == 1 （已递归到目标层），当前节点就是第 k 层的节点，返回 1。

否则，第 k 层节点数 = 左子树第 k-1 层的节点数 + 右子树第 k-1 层的节点数（通过递归

将 k 逐层减 1，直到 k=1 时统计）。

结合示例二叉树的执行流程以先前的二叉树（结构： A 为第 1 层； B 、 C 为第

层； D 、 E 、 F 为第 3 层）为例，计算不同 k 值的结果：

示例 1：计算第 2 层节点数（k=2）

从根 A 开始， k=2≠1 ，递归计算左子树（ B ）的第 2-1=1 层节点数 + 右子树（ C ）的第

1 层节点数。

B 的第 1 层： B 非空且 k=1 ，返回 1。
C 的第 1 层： C 非空且 k=1 ，返回 1。
结果： 1+1=2 （第 2 层节点为 B 、 C ，正确）。

示例 2：计算第 3 层节点数（k=3）

从根 A 开始， k=3≠1 ，递归计算左子树（ B ）的第 3-1=2 层 + 右子树（ C ）的第 2 层节点

数。

左子树 B 的第 2 层： B 的 k=2≠1 ，递归计算 B 的左子树（ D ）的第 2-1=1 层（ D 非空，

返回 1） + B 的右子树（ NULL ）的第 1 层（返回 0） → 结果 1+0=1。

右子树 C 的第 2 层： C 的 k=2≠1 ，递归计算 C 的左子树（ E ）的第 1 层（返回 1） + C 的

右子树（ F ）的第 1 层（返回 1） → 结果 1+1=2。

总结果： 1+2=3 （第 3 层节点为 D 、 E 、 F ，正确）。

总结:

函数通过"将 k 逐层递减"的递归方式，把"求第 k 层节点数"转化为"求左右子树第 k-1 层节点数之

和"，逻辑简洁且高效，时间复杂度为 O(n) （需遍历树中相关节点）。只要明确"根为第 1 层"，就

能准确统计任意第 k 层的节点数量。

8. 统计二叉树的深度/高度---BinaryTreeDepth函数
cs 复制代码
int BinaryTreeDepth(BTNode* root)
{
    // 1. 空树：深度为 0
    if (root == NULL)
    {
        return 0;
    }
    // 2. 递归计算左子树深度
    int leftDep = BinaryTreeDepth(root->left);
    // 3. 递归计算右子树深度
    int rightDep = BinaryTreeDepth(root->right);
    // 4. 整棵树深度 = 1（当前节点） + 左右子树的最大深度
    return 1 + (leftDep > rightDep ? leftDep : rightDep);
}
这个函数用于计算二叉树的深度（也叫高度，即从根节点到最远叶子节点的最长路径上的节

点总数），核心逻辑是通过递归比较左右子树的深度，取较大值加 1（当前节点本身）作为

整棵树的深度。以下详细说明：

核心逻辑:

若树为空（ root == NULL ），深度为 0。

否则，先递归计算左子树的深度（ leftDep ）和右子树的深度（ rightDep ）。

整棵树的深度 = 1（当前节点） + 左右子树中较深的那个的深度（通过三元表达式 leftDep

>rightDep ? leftDep : rightDep 取最大值）。

结合示例二叉树的执行流程，以先前的二叉树（结构： A 为根， B 、 C 为第 2 层； B 有

D ， C 有 E 、 F ，所有叶子在第 3 层）为例：

计算左子树（ B 分支）深度：

B 的左子树是 D ， D 的左右子树均为空（深度 0） → D 的深度 = 1 + max(0, 0) = 1。
B 的右子树为空（深度 0） → B 的深度 = 1 + max( D 的深度 1, 0) = 2。

计算右子树（ C 分支）深度：

E 和 F 的左右子树均为空（深度 0） → E 、 F 的深度均为 1。
C 的左子树是 E （深度 1），右子树是 F （深度 1） → C 的深度 = 1 + max(1, 1) = 2。

计算整棵树（ A ）的深度：

A 的左子树深度是 2（ B 分支），右子树深度是 2（ C 分支） → A 的深度 = 1 + max(2, 2) =

3。

结果与实际深度（根到叶子最长路径为 3 层）一致。

总结:

函数通过递归将"整棵树的深度"拆解为"1 + 左右子树的最大深度"，本质是找到从根到最远叶子的路

径长度，逻辑清晰且高效。

9. 二叉树查找值为x的结点函数---BinaryTreeFind函数
cs 复制代码
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
    // 1. 空树：找不到节点，返回 NULL
    if (root == NULL)
    {
        return NULL;
    }
    // 2. 当前节点就是目标：返回该节点指针
    if (root->data == x)
    {
        return root;
    }
    // 3. 左子树中查找
    BTNode* leftFind = BinaryTreeFind(root->left, x);
    if (leftFind)  // 左子树找到，直接返回
    {
        return leftFind;
    }
    // 4. 左子树没找到，在右子树中查找
    BTNode* rightFind = BinaryTreeFind(root->right, x);
    if (rightFind)  // 右子树找到，返回
    {
        return rightFind;
    }
    // 5. 左右子树都没找到，返回 NULL
    return NULL;
}
这个函数用于在二叉树中查找值为 x 的节点，返回该节点的指针（若找不到则返回

NULL ），核心逻辑是通过递归遍历树的所有节点，优先检查当前节点，再依次搜索左、右

子树。以下详细说明：

核心逻辑:

若树为空（ root == NULL ），返回 NULL （找不到目标）。

若当前节点的值等于 x （ root->data == x ），返回当前节点的指针（找到目标）。

否则，先递归在左子树中查找（ leftFind ）：

若左子树中找到（ leftFind 非空），直接返回 leftFind 。

若左子树中没找到，再递归在右子树中查找（ rightFind ），找到则返回 rightFind ，否则

返回 NULL 。

结合示例二叉树的执行流程，以之前的二叉树（节点值： A 、 B 、 C 、 D 、 E 、 F ）为例，假

设查找 E ：

从根 A 开始：

A->data 是 A ≠ E ，递归查找左子树（ B 分支）。

查找 B 分支：

B->data 是 B ≠ E ，递归查找 B 的左子树（ D ）。

D->data 是 D ≠ E ， D 的左右子树为空 → 左、右查找均返回 NULL ，即 B 分支查找结果

为 NULL 。

查找 C 分支：

左子树（ B 分支）没找到，递归查找 A 的右子树（ C ）。

C->data 是 C ≠ E ，递归查找 C 的左子树（ E ）。
E->data 是 E → 找到目标，返回 E 的指针。

总结:

函数采用先序遍历的思路（先查当前节点，再左、再右）查找目标节点，确保遍历所有节点直到找

到为止。若树中存在多个值为 x 的节点，会返回第一个被遍历到的节点（即左子树中出现的节点

优先于右子树）。时间复杂度为 O(n) （最坏情况需遍历所有节点），是二叉树节点查找的基础实

现。

10. ⼆叉树销毁函数---BinaryTreeDestory函数
cs 复制代码
void BinaryTreeDestory(BTNode** root)
{
    // 1. 若当前节点为空（或已释放），直接返回
    if (*root == NULL)
    {
        return;
    }
    // 2. 递归销毁左子树（传入左孩子的地址）
    BinaryTreeDestory(&((*root)->left));
    // 3. 递归销毁右子树（传入右孩子的地址）
    BinaryTreeDestory(&((*root)->right));
    // 4. 释放当前节点的内存
    free(*root);
    // 5. 将当前节点指针置空（避免野指针）
    *root = NULL;
}
这个函数用于销毁二叉树（释放所有节点的内存，并将根指针置空），核心逻辑是通过递归

先销毁左右子树，再释放当前节点，避免内存泄漏。以下详细说明：

核心逻辑:

采用"后序遍历"的思路：先递归销毁左子树，再递归销毁右子树，最后释放当前节点的内

存，并将该节点指针置空（防止野指针）。

函数参数用二级指针（ BTNode** root ），因为需要通过指针修改外部传入的根节点指针

（最终将其置为 NULL ）。

执行流程（以示例二叉树为例）:

销毁左子树（ B 分支）：

先递归销毁 B 的左子树（ D ）： D 的左右子树为空，直接释放 D 并置空。
再递归销毁 B 的右子树（ NULL ）：直接返回。
最后释放 B 并置空。

销毁右子树（ C 分支）：

先递归销毁 C 的左子树（ E ）： E 的左右子树为空，释放 E 并置空。
再递归销毁 C 的右子树（ F ）： F 的左右子树为空，释放 F 并置空。
最后释放 C 并置空。

销毁根节点 A ：

左右子树均已销毁，释放 A 的内存，并将根指针（外部传入的 *root ）置为 NULL 。

**关键细节:

用二级指针的原因：若用一级指针， free 后只能修改函数内部的指针副本，无法将外部的根指**

针置空，可能导致野指针错误。

- 后序销毁的必要性：必须先销毁子树再释放当前节点，否则释放当前节点后，无法访问其左右孩

子指针，导致子树内存无法释放（内存泄漏）。

通过这种方式，能确保二叉树的所有节点都被正确释放，且根指针最终被置空，是销毁二叉树的标

准安全实现。

以上便是实现文件中所有函数的详细内容。

1.3 测试文件---test.c

cs 复制代码

#define _CRT_SECURE_NO_WARNINGS
#include"Tree.h"

//创建相应的节点并初始化
BTNode* buyNode(char x)
{
    BTNode* node = (BTNode*)malloc(sizeof(BTNode));
    if (node == NULL)
    {
        printf("malloc failed\n");
        return NULL;
    }
    node->data = x;
    node->left = node->right = NULL;


    return node;
}

BTNode* createBinaryTree()
{
    BTNode* nodeA = buyNode('A');
    BTNode* nodeB = buyNode('B');
    BTNode* nodeC = buyNode('C');
    BTNode* nodeD = buyNode('D');
    BTNode* nodeE = buyNode('E');
    BTNode* nodeF = buyNode('F');


    nodeA->left = nodeB;
    nodeA->right = nodeC;
    nodeB->left = nodeD;
    nodeC->left = nodeE;
    nodeC->right = nodeF;

    return nodeA;  //返回头结点

}

void test01()
{
    BTNode* root = createBinaryTree();    //将nodeA赋值为头结点
    preOrder(root);
    printf("\n");
    inOrder(root);
    printf("\n");
    postOrder(root);
    printf("\n");
    printf("size:%d\n", BinaryTreeSize(root));      //二叉树结点个数
    printf("Leaf size:%d\n", BinaryTreeLeafSize(root));  //二叉树叶子节点个数
    printf("K size:%d\n", BinaryTreeLevelKSize(root, 1));    //二叉树第K层结点的个数
    printf("depth:%d\n", BinaryTreeDepth(root));   //二叉树的深度/高度
    if (BinaryTreeFind(root, 'G'))
    {
        printf("找到了\n");
    }
    else
    {
        printf("未找到\n");
    }

    BinaryTreeDestory(&root);
}

int main()
{
    test01();
    return 0;
}

这个测试文件是用于验证二叉树相关操作函数功能的代码，主要流程是：先手动创建一棵固定结构

的二叉树，然后调用之前实现的各种二叉树操作函数（遍历、统计、查找、销毁等），通过输出结

果验证这些函数是否正确工作。以下分部分解释：

1. 头文件与节点创建函数

cs 复制代码

-  #define _CRT_SECURE_NO_WARNINGS   //屏蔽VS编译器的安全警告（如 malloc 相关）。
-  #include"Tree.h"    //包含二叉树的头文件（里面应定义了 BTNode 结构体、各种操作函数的声明等）。
-  buyNode(char x) ：
功能是创建一个二叉树节点，为节点分配内存，初始化节点值为 x ，左右孩子指针置为 NULL 。若内存分配失败（ malloc 返回 NULL ），打印错误信息。

2. 二叉树创建函数 createBinaryTree()

手动创建一棵固定结构的二叉树，节点值为 A 到 F ，具体结构如下：

/ \

B C

/ / \

D E F

步骤：先调用 buyNode 创建 A 到 F 六个节点，再通过指针赋值建立节点间的关系（ A 的左孩子

是 B 、右孩子是 C ； B 的左孩子是 D ； C 的左孩子是 E 、右孩子是 F ）。

最后返回根节点 A 的指针，作为整棵树的入口。

3. 测试函数 test01()

这是核心测试逻辑，分步骤验证二叉树操作：

创建二叉树： BTNode* root = createBinaryTree() 得到根节点 root （即节点 A ）。
遍历测试：

调用前序遍历（ preOrder ）、中序遍历（ inOrder ）、后序遍历（ postOrder ）函数，打印遍历

结果，验证遍历逻辑是否正确。

统计功能测试：

BinaryTreeSize(root) ：输出总节点数（预期结果为6，因为有 A-F 6个节点）。
BinaryTreeLeafSize(root) ：输出叶子节点数（预期结果为3，叶子节点是 D、E、F ）。
BinaryTreeLevelKSize(root, 1) ：输出第1层节点数（预期结果为1，只有根节点 A ）。
BinaryTreeDepth(root) ：输出树的深度（预期结果为3，从根 A 到叶子 D/E/F 共3层）。

查找功能测试：

调用 BinaryTreeFind(root, 'G') 查找值为 G 的节点（树中不存在 G ），预期输出"未找到"。

销毁二叉树：

调用 BinaryTreeDestory(&root) 释放整棵树的内存，并将根指针 root 置空，避免野指针。

下面我们来验证一下编译器所给出的答案:

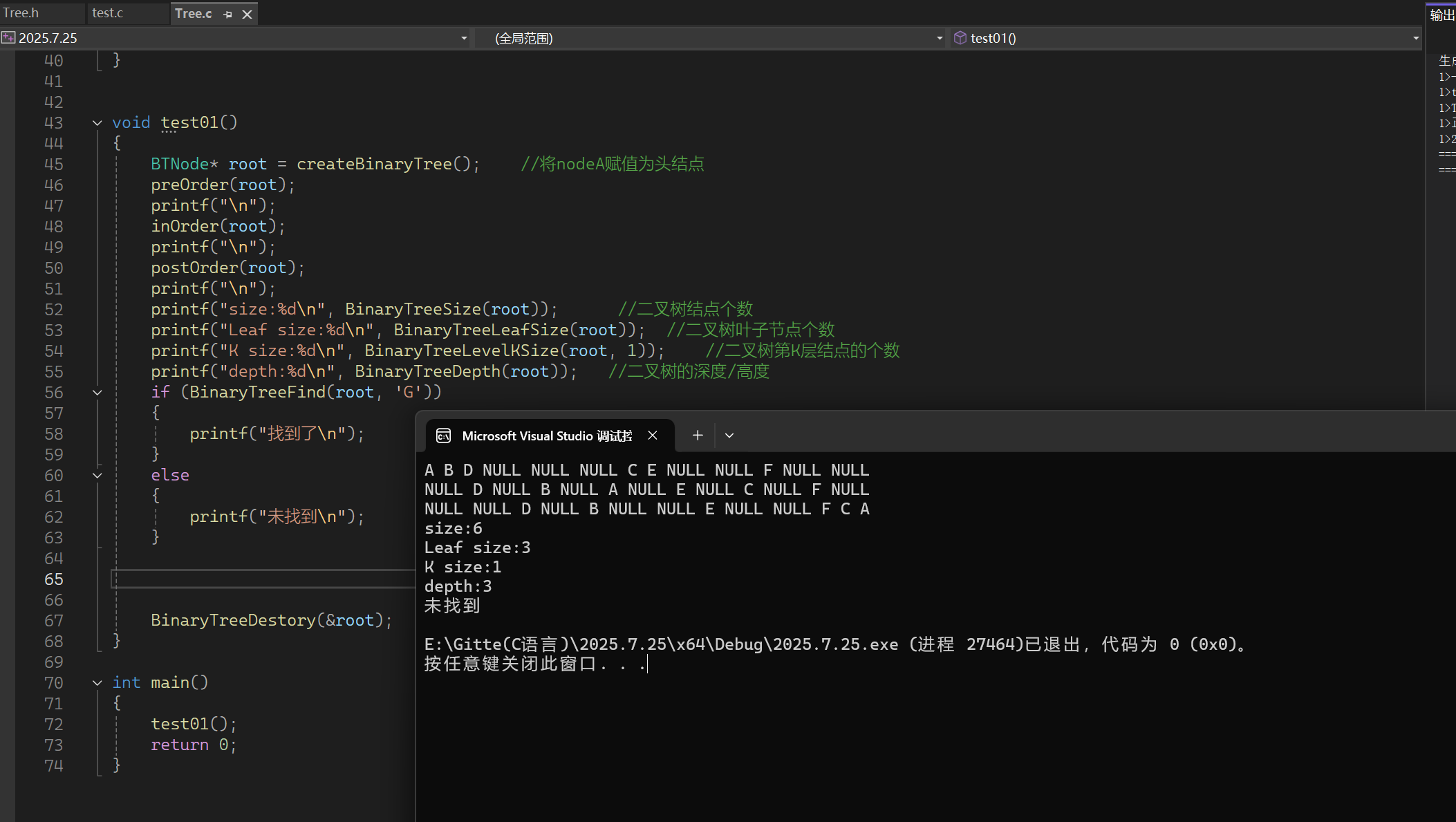
由此可知与我们的推测完全一致。

4. 主函数 main()

仅调用 test01() 函数，执行整个测试流程，程序运行后会输出所有测试结果，通过观察输出是否符

合预期（如节点数、遍历顺序等），即可验证之前实现的二叉树操作函数是否正确。

总结:

这个测试文件是一个"一站式验证工具"，通过手动构建已知结构的二叉树，调用各种操作函数并输

出结果，直观地检验函数功能的正确性，是数据结构中验证算法实现的常用方式。

2. 总结:

以上便是关于整个用链式结构实现二叉树的完整内容。下面小编把完整版的代码留给大家：

以下是用链式结构实现二叉树的完整代码，包含头文件（ Tree.h ）、功能实现文件（ Tree.c ）和

测试文件（ test.c ），整合了之前提到的所有操作函数，逻辑完整可直接使用：

2.1 头文件---Tree.h

cs 复制代码

#pragma once
#pragma once
#include<stdio.h>
#include<stdlib.h>

//定义链式结构的二叉树

typedef char BTDataType;
typedef struct BinaryTreeNode
{
    BTDataType data;
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
}BTNode;

//前序遍历
void preOrder(BTNode* root);
//中序遍历
void inOrder(BTNode* root);
//后序遍历
void postOrder(BTNode* root);


//二叉树结点个数
int BinaryTreeSize(BTNode* root);
//int BinaryTreeSize(BTNode* root,int* psize);

//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root);

//二叉树第K层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k);

////二叉树的深度/高度
int BinaryTreeDepth(BTNode* root);

//二叉树查找值为X的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x);

//二叉树的销毁
void BinaryTreeDestory(BTNode** root);

2.2 实现文件---Tree.c

cs 复制代码

#define _CRT_SECURE_NO_WARNINGS

#define _CRT_SECURE_NO_WARNINGS
#include"Tree.h"

//前序遍历
void preOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
    printf("%c ", root->data);
    preOrder(root->left);
    preOrder(root->right);
}


//中序遍历
void inOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
    inOrder(root->left);
    printf("%c ", root->data);
    inOrder(root->right);
}


//后序遍历
void postOrder(BTNode* root)
{
    if (root == NULL)
    {
        printf("NULL ");
        return;
    }
    postOrder(root->left);
    postOrder(root->right);
    printf("%c ", root->data);
}



//二叉树结点个数
//法一:
//int size = 0;
//int BinaryTreeSize(BTNode* root)
//{
//    if (root == NULL)
//    {
//        return 0;
//    }
//    //结点非空, +1
//    size++;
//    BinaryTreeSize(root->left);
//    BinaryTreeSize(root->right);
//
//
//    return size;
//}
////法二:
//int BinaryTreeSize(BTNode* root, int* psize)
//{
//    if (root == NULL)
//    {
//        return 0;
//    }
//    //结点非空
//    (*psize)++;
//    BinaryTreeSize(root->left);
//    BinaryTreeSize(root->right);
//
//
//    return psize;
//}
//法三:
int BinaryTreeSize(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }

    return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}


//二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    if (root->left == NULL && root->right == NULL)
    {
        return 1;
    }
    return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

//二叉树第K层结点的个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
    if (root == NULL)
    {
        return 0;
    }
    if (k == 1)
    {
        return 1;
    }
    return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

//二叉树的深度/高度
int BinaryTreeDepth(BTNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    int leftDep = BinaryTreeDepth(root->left);
    int rightDep = BinaryTreeDepth(root->right);

    return 1 + (leftDep > rightDep ? leftDep : rightDep);
}

//二叉树查找值为x的结点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
    if (root == NULL)
    {
        return NULL;
    }
    if (root->data == x)
    {
        return root;
    }
    BTNode* leftFind = BinaryTreeFind(root->left, x);
    if (leftFind)
    {
        return leftFind;
    }
    BTNode* rightFind = BinaryTreeFind(root->right, x);
    if (rightFind)
    {
        return rightFind;
    }
    return NULL;
}

// ⼆叉树销毁--左右根
void BinaryTreeDestory(BTNode** root)
{
    if (*root == NULL)
    {
        return;
    }
    BinaryTreeDestory(&((*root)->left));
    BinaryTreeDestory(&((*root)->right));
    free(*root);
    *root = NULL;
}

2.3 测试文件---test.c

cs 复制代码

#define _CRT_SECURE_NO_WARNINGS
#define _CRT_SECURE_NO_WARNINGS
#include"Tree.h"

//创建相应的节点并初始化
BTNode* buyNode(char x)
{
    BTNode* node = (BTNode*)malloc(sizeof(BTNode));
    if (node == NULL)
    {
        printf("malloc failed\n");
        return NULL;
    }
    node->data = x;
    node->left = node->right = NULL;


    return node;
}


BTNode* createBinaryTree()
{
    BTNode* nodeA = buyNode('A');
    BTNode* nodeB = buyNode('B');
    BTNode* nodeC = buyNode('C');
    BTNode* nodeD = buyNode('D');
    BTNode* nodeE = buyNode('E');
    BTNode* nodeF = buyNode('F');


    nodeA->left = nodeB;
    nodeA->right = nodeC;
    nodeB->left = nodeD;
    nodeC->left = nodeE;
    nodeC->right = nodeF;

    return nodeA;  //返回头结点

}


void test01()
{
    BTNode* root = createBinaryTree();    //将nodeA赋值为头结点
    preOrder(root);
    printf("\n");
    inOrder(root);
    printf("\n");
    postOrder(root);
    printf("\n");
    printf("size:%d\n", BinaryTreeSize(root));      //二叉树结点个数
    printf("Leaf size:%d\n", BinaryTreeLeafSize(root));  //二叉树叶子节点个数
    printf("K size:%d\n", BinaryTreeLevelKSize(root, 1));    //二叉树第K层结点的个数
    printf("depth:%d\n", BinaryTreeDepth(root));   //二叉树的深度/高度
    if (BinaryTreeFind(root, 'G'))
    {
        printf("找到了\n");
    }
    else
    {
        printf("未找到\n");
    }



    BinaryTreeDestory(&root);
}

int main()
{
    test01();
    return 0;
}

三个文件分工明确： Tree.h 声明接口， Tree.c 实现功能， test.c 验证正确性。
编译时需将三个文件一起编译（如 gcc Tree.c test.c -o tree_test ），运行可执行文件即可看到测

试结果。

代码涵盖了二叉树的核心操作，可直接作为链式结构实现二叉树的参考模板。

总结:

这套实现完整覆盖了链式二叉树的基础操作，通过递归思想简化了遍历和统计逻辑，文件结构清

晰、分工明确，既便于理解二叉树的工作原理，也可作为实际开发中链式二叉树实现的参考模板。

数据结构 二叉树(2)---二叉树的实现

1. 链式结构实现二叉树

1.1 头文件---Tree.h

1. 头文件保护宏

2. 包含标准库

3. 定义二叉树节点的数据类型

4. 定义二叉树节点的结构体

5. 函数声明

(1）遍历函数（前序、中序、后序）

(2）统计类函数

(3）查找与销毁函数

6. 整体逻辑："声明 + 实现分离"

1.2 实现文件---Tree.c

1. 遍历的思想

2. 前序遍历函数---preOrder函数

3. 中序遍历函数---inOrder函数

4. 后序遍历函数---postOrder函数

5. 统计二叉树结点个数函数---BinaryTreeSize函数

6. 统计二叉树叶子节点个数---BinaryTreeLeafSize函数

7. 二叉树第K层结点的个数函数---BinaryTreeLevelKSize函数

8. 统计二叉树的深度/高度---BinaryTreeDepth函数

9. 二叉树查找值为x的结点函数---BinaryTreeFind函数

10. ⼆叉树销毁函数---BinaryTreeDestory函数

1.3 测试文件---test.c

1. 头文件与节点创建函数

2. 二叉树创建函数 createBinaryTree()

3. 测试函数 test01()

4. 主函数 main()

2. 总结:

2.1 头文件---Tree.h

2.2 实现文件---Tree.c

2.3 测试文件---test.c

数据结构二叉树(2)---二叉树的实现