韦恩图的应用
由于事件的计算有时候太过于抽象了,此时我们可以使用韦恩图的方式来进行验证,我们下面来举一个例子,A∪B)-C=A∪(B-C)是否成立?我们可以通过韦恩图来完成这个任务:
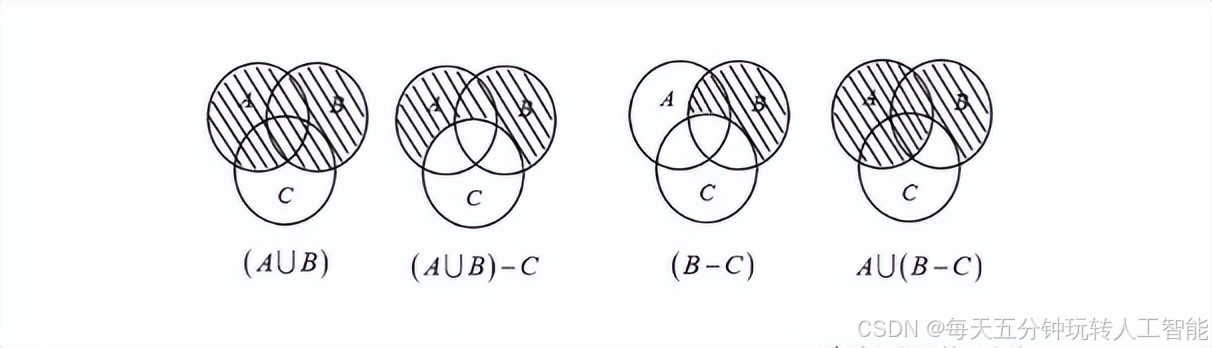
我们通过这种方式来一点一点的比较,我们可以看到二者根本就不相等。
AB杠和A杠B杠之间的区别?
AB表示AB同时发生,AB杠表示AB不同时发生(覆盖范围大)
A杠B杠表示A、B都不发生(覆盖范围小)
我们也可以通过韦恩图的方式来将二者给画出来

三个事件之间的关系
交翻译为同时,并翻译为或者
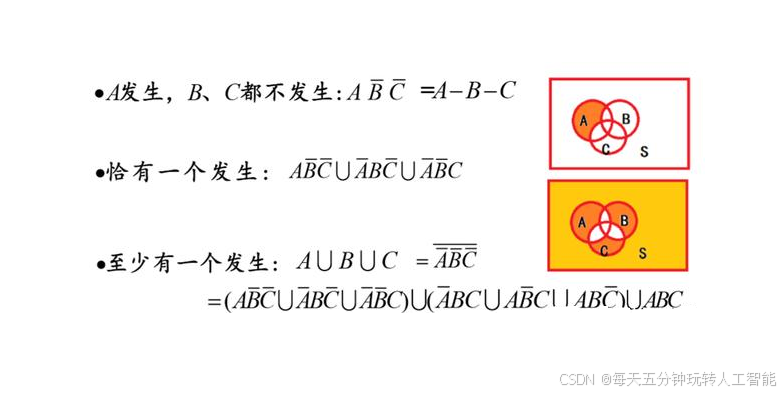
恰有一个发生就是只有一个发生(其它的不能发生),至少一个发生就是最少有一个发生(其它的爱发生不发生)

以上就是概率论之韦恩图的应用