译|生存分析Survival Analysis案例入门讲解（一）

文章出自：出自：Survival Analysis: Predict Time-To-Event With Machine Learning (Part I)

本文技术亮点在于结合生存分析与机器学习，既能处理部分数据缺失（删失），又能预测事件发生的具体时间，提升了模型的实际应用价值。该方法适合需要预测"什么时候会发生某事"的场景，帮助企业提前采取行动。典型商业应用包括客户流失预测、设备故障预警、患者复诊时间预测等。比如在客户流失案例中，模型能预测客户未来不同时间点的流失概率，助力精准营销和资源分配，提升客户留存率。

---

文章目录

• • 实际应用：客户流失预测
  • 目标
  • [1. 生存分析是什么？](#1. 生存分析是什么？)
  • • [1.1 问题描述](#1.1 问题描述)
    • [1.2 应用场景](#1.2 应用场景)
  • [2. 常见生存分析方法](#2. 常见生存分析方法)
  • • [2.1 Kaplan-Meier估计器](#2.1 Kaplan-Meier估计器)
    • [2.2 Cox比例风险模型](#2.2 Cox比例风险模型)
  • [3. 机器学习如何应用于生存分析？](#3. 机器学习如何应用于生存分析？)
  • • [3.1 基于机器学习的生存模型](#3.1 基于机器学习的生存模型)
    • [随机生存森林（Random Survival Forests）](#随机生存森林（Random Survival Forests）)
    • [梯度提升生存分析（Gradient Boosting Survival Analysis）](#梯度提升生存分析（Gradient Boosting Survival Analysis）)
    • [生存支持向量机（Survival Support Vector Machine）](#生存支持向量机（Survival Support Vector Machine）)
    • [3.2 模型比较](#3.2 模型比较)
    • • 方法论
      • [一致性指数（Concordance index）](#一致性指数（Concordance index）)
      • 累计/动态AUC
  • 关键总结

---

实际应用：客户流失预测

预测事件发生的概率固然重要，但如果能预测事件发生前剩余的时间，那就更好了！

以客户流失为例。假如你不仅能预测客户未来几个月内流失的概率，还能预测他们在未来几个月多个时间点上的流失概率？这种方法的好处立竿见影。它可以让你更有效地提前规划和优先安排营销行动，从而最终降低客户流失率。

这正是生存分析（survival analysis），又称为事件发生时间分析（time-to-event analysis）所涉及的领域。它是一种学习框架和一套技术，用于基于观测数据估计事件发生所需的时间。

"生存分析"这个名称来源于其最初的典型应用场景：临床研究中预测患者的生存时间。然而，名字不要误导你，它不仅限于医疗领域，还可以应用于多个行业的各种用例。随着数据科学的进步，生存分析已重新兴起，超越了传统统计学，融入了更多先进的机器学习方法。

目标

本文重点介绍如何将机器学习与生存分析框架结合，解决如客户流失预测等用例。

阅读本文后，你将了解：

1. 生存分析到底是什么？
2. 主要的生存模型有哪些，它们如何工作？
3. 如何将这些模型具体应用于客户流失预测？

本文是生存分析系列文章的第一部分。理解本文不需要任何先验知识。文中实验使用的库包括 scikit-survival 和 plotly。代码可在 GitHub 找到。

1. 生存分析是什么？

1.1 问题描述

乍一看，生存分析似乎只是另一个回归问题，因为目标是预测事件发生的时间（一个连续变量）。但问题有个转折点：部分训练数据可能是部分观察到的------即存在删失（censoring）。

举个例子，假设一家公司提供订阅制服务，想要预测每个联系过客服的客户在未来一段时间内的退订概率。在数据收集期间：

• 客户A在研究结束前未退订。
• 客户B和D在几个月后取消了订阅。
• 客户C选择限制平台访问其数据。

在这种情况下，客户A和C的记录是删失数据。

Zoom image will be displayed

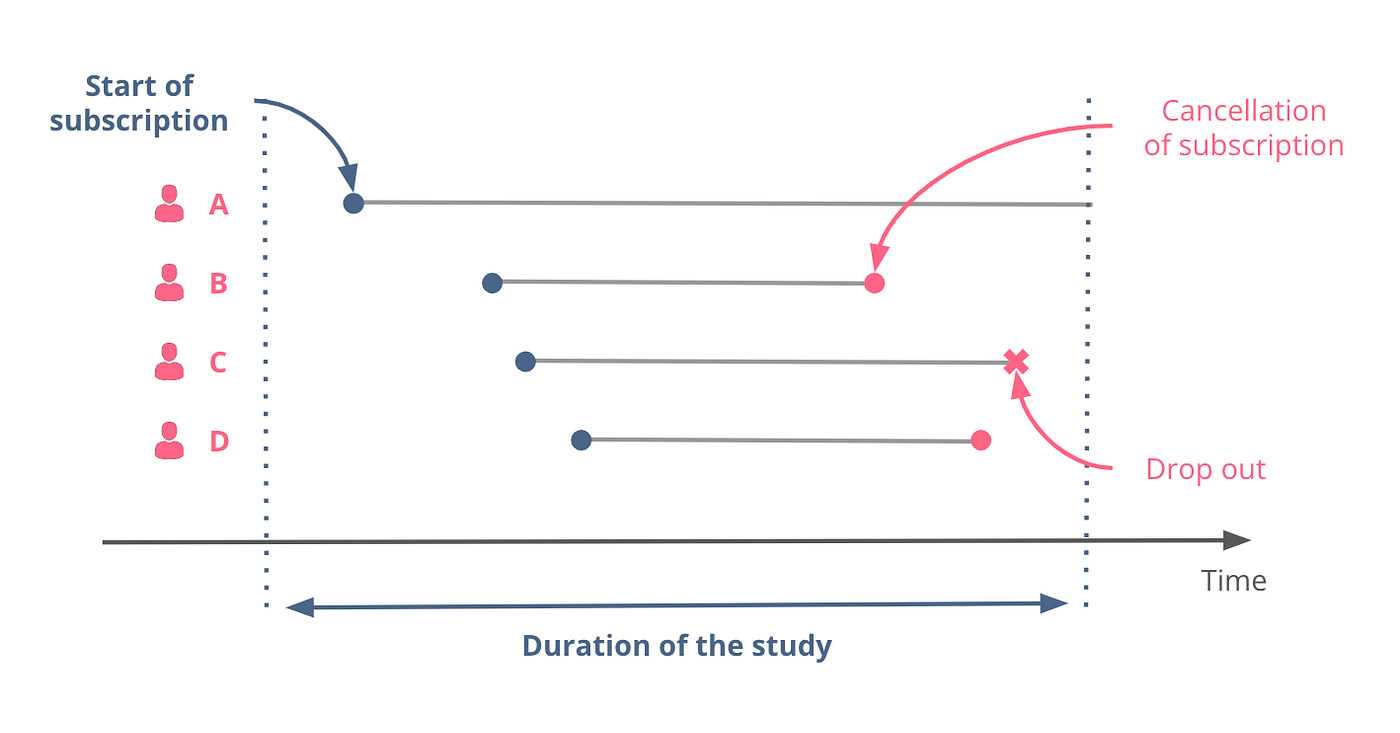
图1 --- 生存分析数据示意，作者绘制

更正式地讲，每条观测数据包含协变量集 X = (x_1, ..., x_n) ，事件发生的时间 t ，或删失时间 c > 0 。引入事件指示符 δ ∈ {0,1}。右删失样本的可观测时间 y 定义为：

Zoom image will be displayed

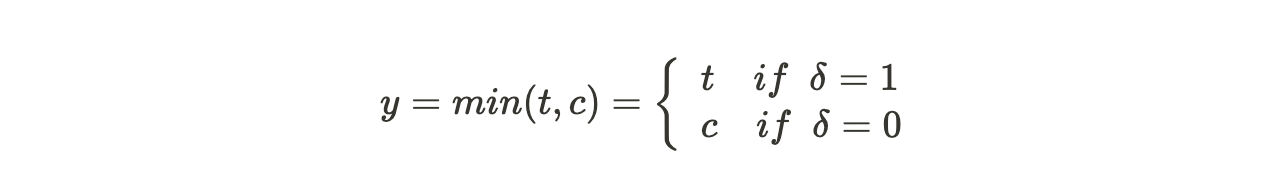
在我们的流失预测案例中，数据包含客户的客服联系历史。每条观测包含信息：

• 交互：日期、通话原因（注册/支持）、渠道（邮箱/电话）。
• 客户：年龄和性别。
• 订阅：产品、价格、计费周期（月度/年度）、注册时间。

数据还被丰富了额外特征，包括客户过去联系公司的次数、订阅持续时间以及周期性日期相关特征。

1.2 应用场景

生存分析适用于预测两个事件之间时间间隔的各种场景，举例如下：

• 预测性维护：预测机器启动后何时可能故障。若机器因外部因素（火警等）停止，数据可能被删失。
• 患者监测：预测患者首次诊断或住院后何时可能再次住院。若患者离开研究地理范围，数据可能被删失。
• 营销分析：预测潜在客户首次电话后何时可能转化。若期间客户去世，数据被删失。
• 经济学：预测失业人员找到新工作的时间。若人员退出研究，数据被删失。

2. 常见生存分析方法

2.1 Kaplan-Meier估计器

最简单的方法之一是使用Kaplan-Meier估计器。这是一种非参数方法，专注于近似生存函数。先介绍基本理论，再看应用案例结果。

生存函数

生存函数 S(t) 表示个体在时间 t 后仍存活的概率，或者说持续时间至少为 t 的概率。

Zoom image will be displayed

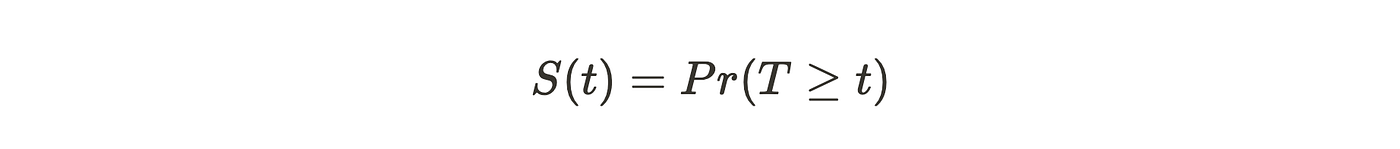
其中 T 是研究群体中的随机寿命。

生存函数 S 在 t=0 时为1，因为开始时没有个体经历事件。随着时间推移，S 递减并趋近于0，因为所有人最终都会经历该事件。

Kaplan-Meier估计器

该模型将生存函数估计拆分为多个小步骤。每个区间的概率计算公式为：

Zoom image will be displayed

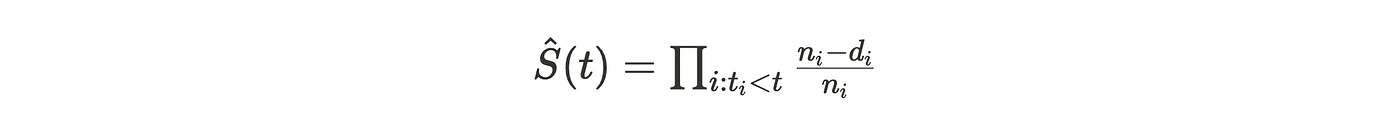
其中 n_i 是时间点 t_i 时的风险个体数，d_i 是该时点经历事件的个体数。

该方法非常简单，不考虑协变量。

• 可用作朴素基线。
• 也可用于数据探索，提供整体生存函数概览或比较不同组。

例如，在本案例中，可以根据订阅计费周期比较估计结果。下图显示月度订阅客户更易流失，且流失速度更快。

Zoom image will be displayed

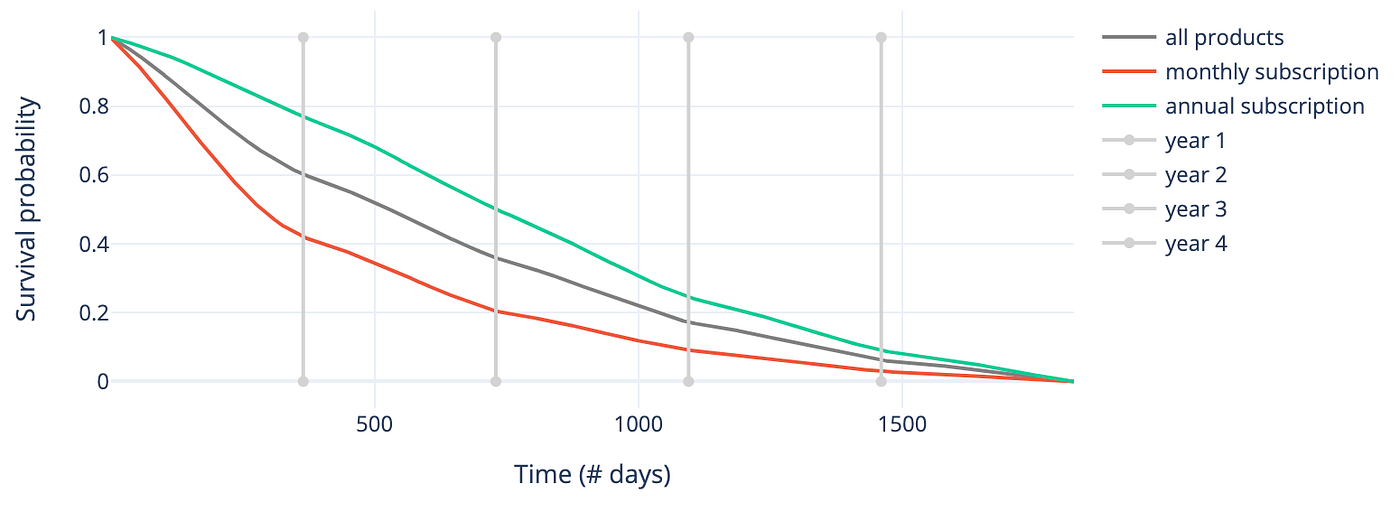
图2 --- Kaplan-Meier模型估计的生存函数

2.2 Cox比例风险模型

最广泛使用的估计器无疑是Cox比例风险（Cox PH）模型。它易于实现，考虑协变量且结果可解释。它是一种半参数方法，旨在建模风险函数。

风险函数

风险函数 h(t) 表示在时间 t 事件发生的概率，条件是个体直到 t 时尚未经历该事件。

Zoom image will be displayed

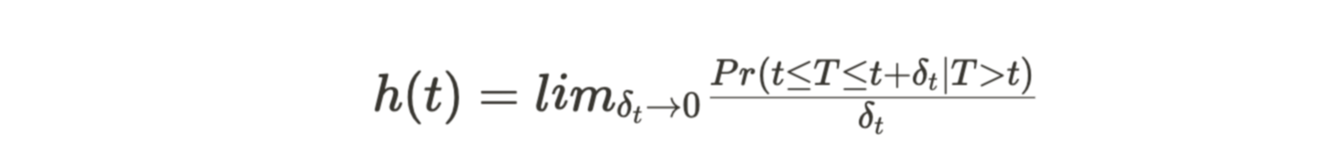
风险函数有助于发现事件发生的安全期或高风险期。

Cox比例风险模型

CoxPH将风险函数建模为：

Zoom image will be displayed

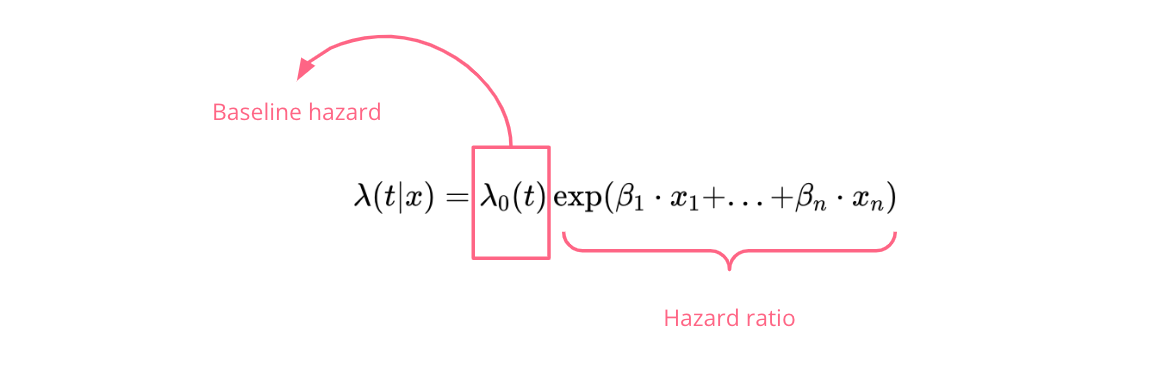
作者插图

模型由两部分组成：

• 基线风险：描述风险随时间的变化。
• 风险比：建模协变量对风险的影响。

该模型依赖强比例假设：在任一时间点，个体的风险函数与基线风险或其他个体风险保持固定比例。

• 例如，如果客户A的初始流失风险是客户B的一半，那么在后续所有时间点，客户A的风险仍是客户B的一半。

应用

模型输出高度可解释。

在个体层面，模型为每条观测提供：

• 风险评分：风险越高，客户越可能流失。
• 生存函数 ：帮助分析师评估客户在时间 t 之后仍存活的概率。例如，下图显示客户2在前几天流失风险最高，而客户1、3、4风险较低。

Zoom image will be displayed

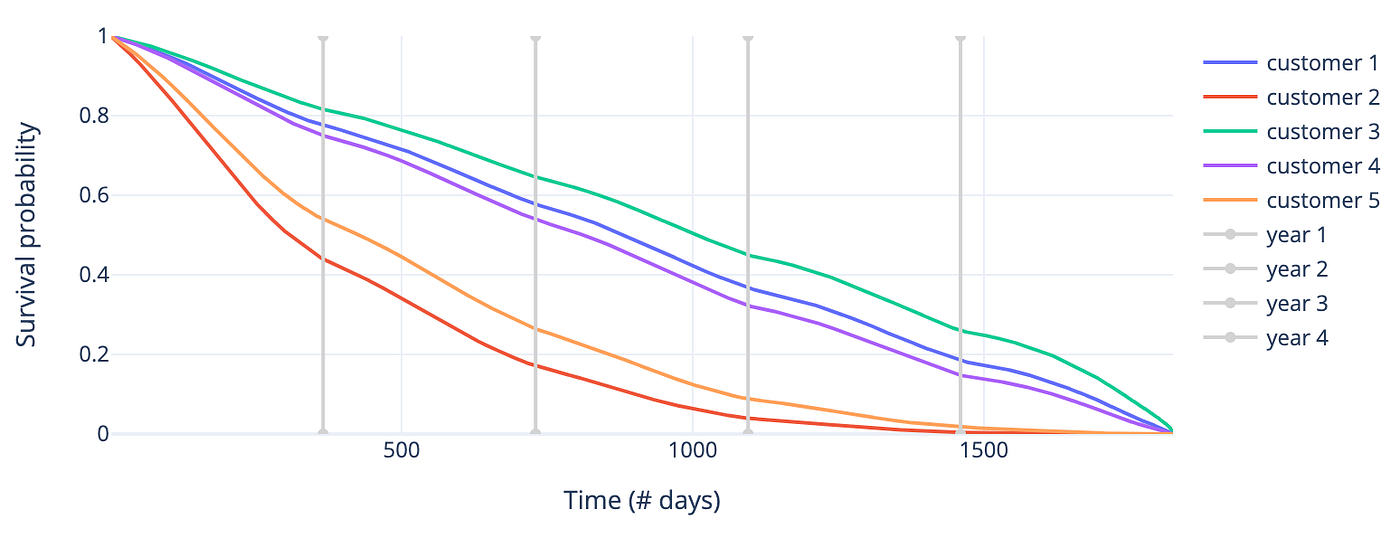
图3 --- 随机选取的5位客户的生存函数

• 风险函数：用途相同。下图验证了上述结论。

Zoom image will be displayed

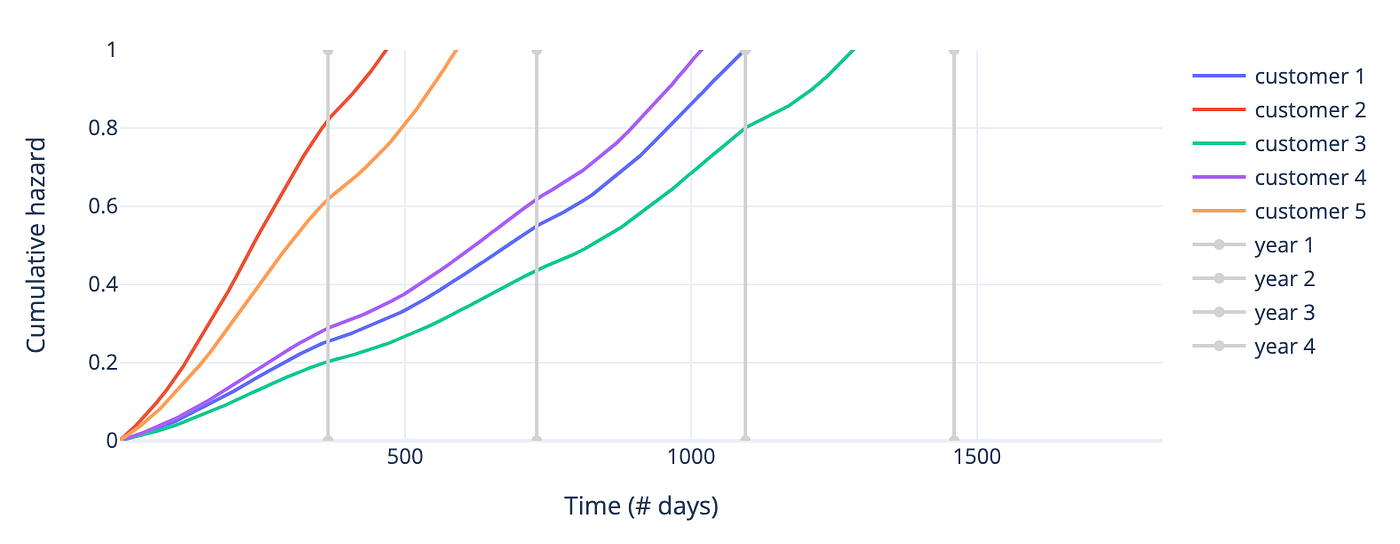
图4 --- 5位客户累计风险函数

在整体层面，模型通过系数解释（见公式）。正系数越大，对流失风险的影响越强。

例如，下图显示模型普遍认为因支持原因联系客户服务是流失风险因素。

Zoom image will be displayed

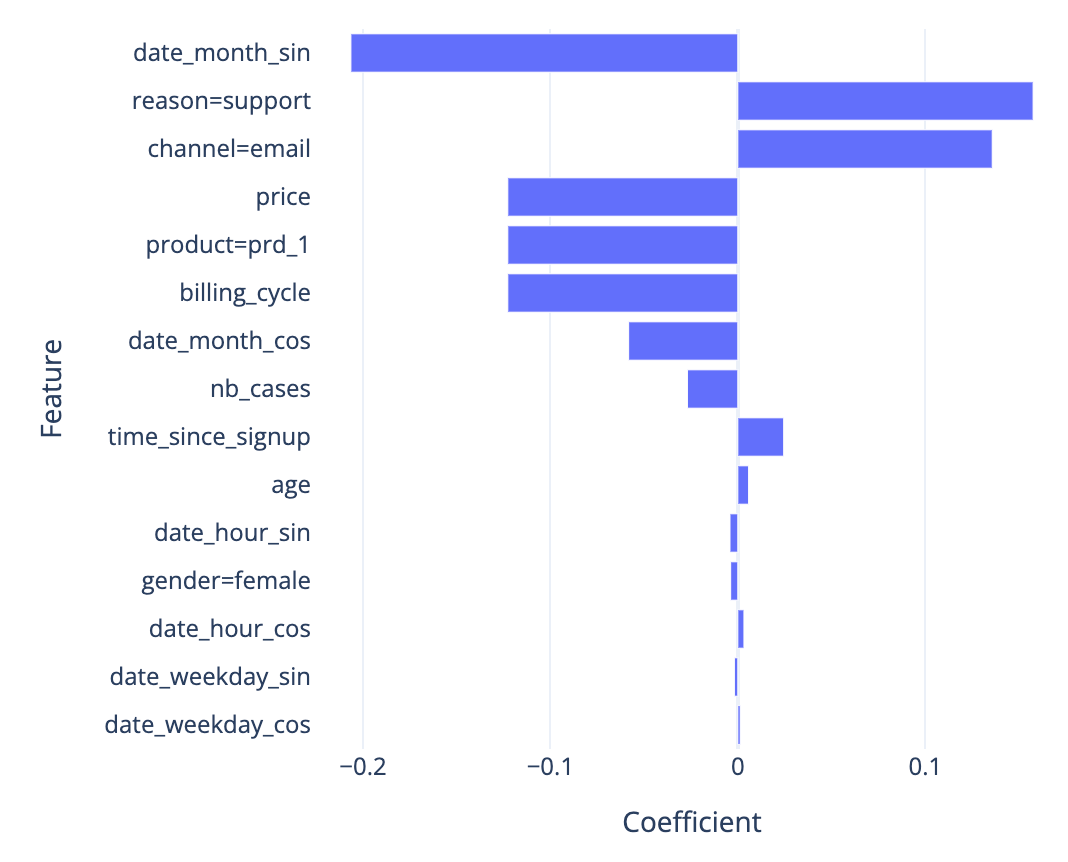
图5 --- Cox PH模型系数

3. 机器学习如何应用于生存分析？

3.1 基于机器学习的生存模型

先介绍机器学习生存模型的基本原理，再比较它们在流失预测案例中的表现。

随机生存森林（Random Survival Forests）

类似于标准的随机森林，随机生存森林训练多个生存树，使用不同子样本（通常有放回抽样），通过平均预测提升准确性并减少过拟合。

主要区别在于用于评估分裂质量的指标：采用log-rank统计，常用于比较两个或多个组的生存曲线。

更多信息见官方文档。

梯度提升生存分析（Gradient Boosting Survival Analysis）

应用于生存分析的梯度提升类似：通过加法方式组合多个弱学习器的预测，构建强模型。弱学习器通常很简单。与随机森林不同，生存树不是独立训练，而是按贪心分阶段顺序训练。

该框架非常灵活，可优化多种损失函数，包括：

• Cox比例风险模型的部分似然损失
• 平方回归损失
• 删失加权最小二乘误差（Inverse Probability of Censoring Weighted Least Squares），也称加速失效时间（Accelerated Failure Time, AFT）模型。该损失允许模型通过常数因子加速或减缓事件时间，与Cox模型只考虑特征对风险函数影响不同。

更多信息见官方文档。

生存支持向量机（Survival Support Vector Machine）

支持向量机（SVM）也可扩展到生存分析。它同样灵活，能通过核技巧捕捉特征与生存的复杂非线性关系。

但其预测结果难以直接关联到生存分析的标准量，如生存函数和累计风险函数。

更多信息见官方文档。

3.2 模型比较

方法论

为比较模型性能，初始数据集约32万条记录，按70%训练集、30%验证集划分，保证删失分布一致。模型使用5折交叉验证调优，随后在验证集评估。

一致性指数（Concordance index）

最常用的评价指标是一致性指数（c-index），衡量模型基于风险评分对生存时间排序的准确性。它是数据集中一致对的比例。

具体来说，考虑两条观测 (i, j)：

• 首先，为可比，较短生存时间的观测必须经历事件。
• 其次，若可比，若模型为生存时间较短者预测更高风险，则该对一致。

下图展示模型在5折交叉验证和验证集上的结果。梯度提升模型表现最佳，c-index约为0.70。

Zoom image will be displayed

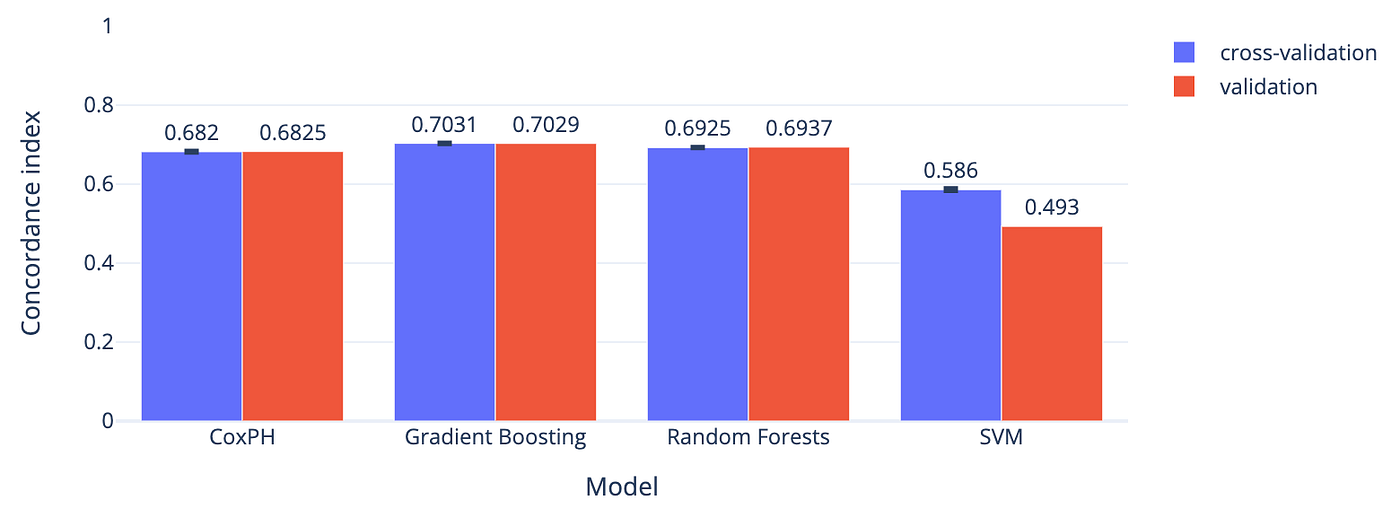
图6 --- 各模型一致性指数

c-index易于计算和理解，但有两个主要缺点：

1. 随删失比例增加，c-index偏向过于乐观。可用删失概率加权法改进，删失分布由训练数据的Kaplan-Meier估计得到。
2. 当目标是评估特定时间段内（如订阅第一年内）预测性能时，c-index帮助有限。

第二个缺点可用累计/动态AUC指标克服。

累计/动态AUC

经典的ROC曲线可扩展到删失的生存时间。思路是在多个时间点分别考虑：

• 累计病例：所有在时间 t 前或 t 时经历事件的个体。
• 动态对照：事件将在时间 t 后发生的个体。

据此评估模型区分未来事件发生者（敏感度）与非发生者（特异度）的能力。

该方法允许只在关键时间点（如前两年）评估模型。

下图显示验证集上模型的时间动态AUC。梯度提升依然表现最佳，前两年平均AUC约0.80。虽然随机森林和Cox PH平均表现相近，但在订阅初期几个月明显落后于梯度提升。

Zoom image will be displayed

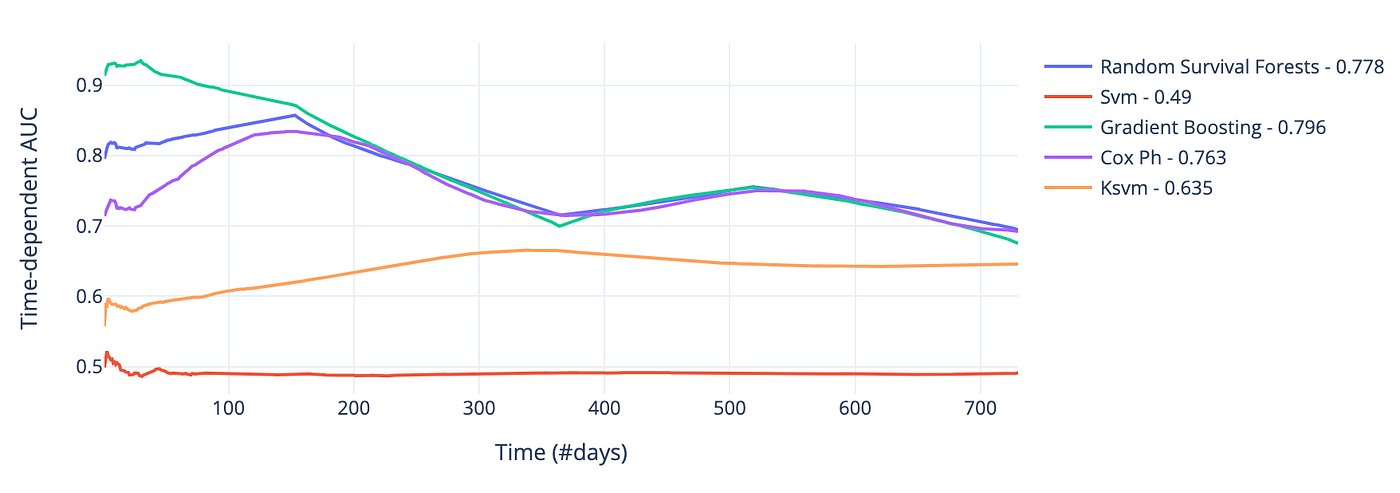
图7 --- 验证集上各模型随时间的AUC

关键总结

✔️ 生存分析是一种学习框架和技术集合，用于基于观测估计事件发生所需时间。

✔️ 它不仅是简单的回归预测问题，因为训练数据中部分数据是删失的。

✔️ 诸如随机森林、梯度提升和支持向量机等常见机器学习模型均可扩展到生存分析，获得性能更优且仍具解释性的模型。

✔️ 将生存分析框架与机器学习的预测能力结合，可为预测性维护、患者监测、营销分析、经济学等众多领域带来显著商业价值。