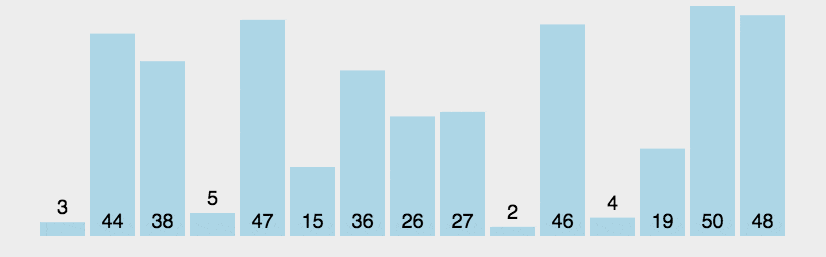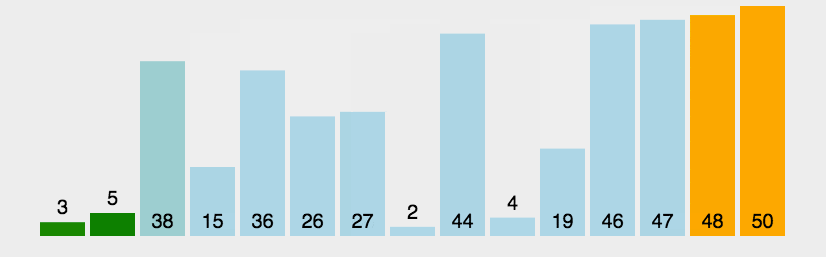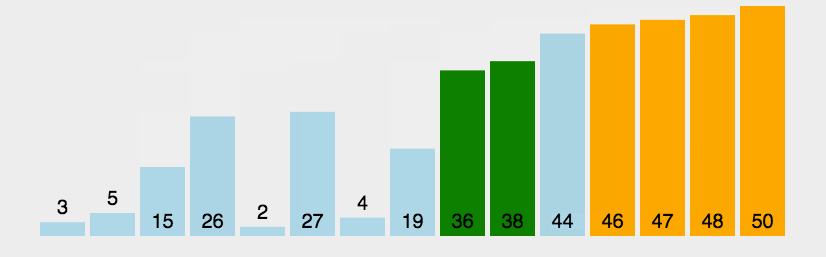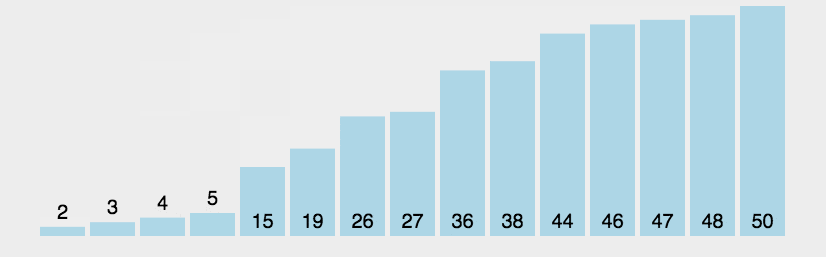【异世界历险之数据结构世界（冒泡、选择、快速排序）】

前言

排序

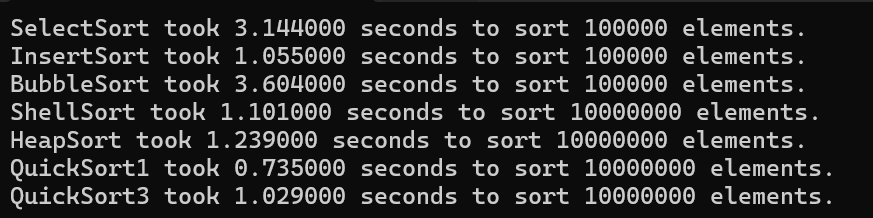
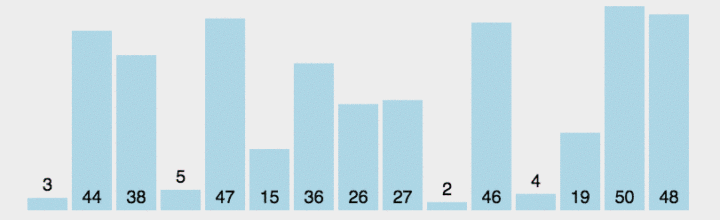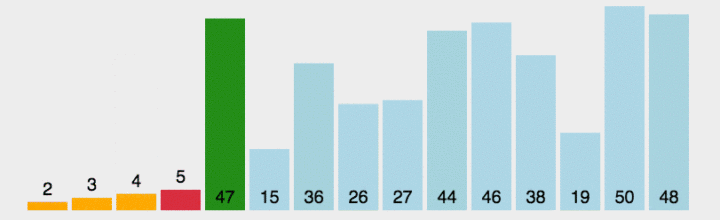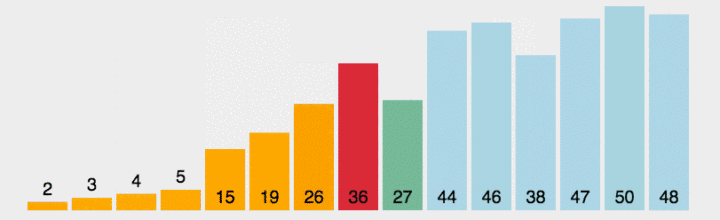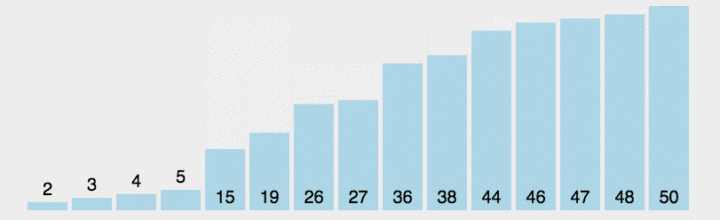
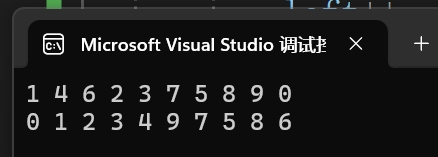
排序效率测试

c 复制代码

void TestTop() {
    srand(time(0));
    const int N1 = 100000;
    const int N2 = 10000000;
    // 动态分配内存并检查
    int* a1 = (int*)malloc(sizeof(int) * N1);
    int* a2 = (int*)malloc(sizeof(int) * N1);
    int* a5 = (int*)malloc(sizeof(int) * N1);

    int* a3 = (int*)malloc(sizeof(int) * N2);
    int* a4 = (int*)malloc(sizeof(int) * N2);
    int* a6 = (int*)malloc(sizeof(int) * N2);
    int* a7 = (int*)malloc(sizeof(int) * N2);
    if (!a1 || !a2 || !a3 ||!a4 ||!a5 ||!a6 ||!a7) {
        printf("Memory allocation failed!\n");
        free(a1);
        free(a2);
        free(a3);
        free(a4);
        free(a5);
        free(a6);
        free(a7);
        return;
    }

    // 填充数组
    for (int i = 0; i < N1; i++) {
        a1[i] = rand();
        a2[i] = a1[i];
        a5[i] = a1[i];
    }

    for (int i = 0; i < N2; i++)
    {
        a3[i] = rand();
        a4[i] = a3[i];
        a6[i] = a3[i];
        a7[i] = a3[i];
    }

    // 测试 SelectSort
    clock_t start_time = clock();
    SelectSort(a1, N1);
    clock_t end_time = clock();
    double time_taken = (double)(end_time - start_time) / CLOCKS_PER_SEC;
    printf("SelectSort took %f seconds to sort %d elements.\n", time_taken, N1);
    free(a1);

    // 测试 InsertSort
    start_time = clock();
    InsertSort(a2, N1);
    end_time = clock();
    time_taken = (double)(end_time - start_time) / CLOCKS_PER_SEC;
    printf("InsertSort took %f seconds to sort %d elements.\n", time_taken, N1);
    free(a2);


    //测试 BubbleSort
    start_time = clock();
    BubbleSort(a5, N1);
    end_time = clock();
    time_taken = (double)(end_time - start_time) / CLOCKS_PER_SEC;
    printf("BubbleSort took %f seconds to sort %d elements.\n", time_taken, N1);
    free(a5);

    // 测试 ShellSort
    start_time = clock();
    ShellSort(a3, N2);
    end_time = clock();
    time_taken = (double)(end_time - start_time) / CLOCKS_PER_SEC;
    printf("ShellSort took %f seconds to sort %d elements.\n", time_taken, N2);
    free(a3);

    //测试 HeapSort
    start_time = clock();
    HeapSort(a4, N2);
    end_time = clock();
    time_taken = (double)(end_time - start_time) / CLOCKS_PER_SEC;
    printf("HeapSort took %f seconds to sort %d elements.\n", time_taken, N2);
    free(a4);

    //测试 QuickSort
    start_time = clock();
    QuickSort1(a6,0,N2-1);
    end_time = clock();
    time_taken = (double)(end_time - start_time) / CLOCKS_PER_SEC;
    printf("QuickSort1 took %f seconds to sort %d elements.\n", time_taken, N2);
    free(a6);

    start_time = clock();
    QuickSort3(a7, 0, N2 - 1);
    end_time = clock();
    time_taken = (double)(end_time - start_time) / CLOCKS_PER_SEC;
    printf("QuickSort3 took %f seconds to sort %d elements.\n", time_taken, N2);
    free(a7);
}

效果展示：

复习+尝试之前的排序

冒泡排序

c 复制代码

void BubbleSort(int* arr,int n)
{
	for (int i = 0; i < n - 1; i++)
	{
		bool swapped = false;
		for (int j = 0; j < n - i - 1; j++)
		{
			if (arr[j] > arr[j + 1])
			{  
				Swap(&arr[j], &arr[j + 1]);
				swapped = true;
			}
		}

		if (!swapped)
		{
			break;
		}
	}
}

冒泡排序（Bubble Sort）代码总结：

基本思想：

通过重复比较相邻元素，若前一个元素大于后一个元素，则交换它们的位置。经过多轮遍历，最大的元素会"冒泡"到数组的末尾，直到数组有序。

代码流程：

外层循环：控制排序的轮次，最多执行 n-1 轮。

内层循环：逐个比较相邻元素，并在需要时进行交换，逐步将较大的元素移动到数组末尾。

交换标记 swapped：用于记录本轮是否发生了交换。如果本轮没有交换，说明数组已经有序，可以提前结束排序。

优化：

如果某一轮没有发生交换，则提前退出循环，减少不必要的比较，提高效率。

时间复杂度：

最坏情况下是 O(n²)，但如果数据接近有序，提前结束的机制能减少计算量。
演示

选择排序

方法一

c 复制代码

void SelectSort(int* arr, int n)
{
	for (int i = 0; i < n-1; i++)
	{
		int mini = i;
	    for (int j = i+1; j < n; j++)
		{
			if (arr[mini] > arr[j])
			{
				mini = j;
			}
		}

		if (mini != i)
		{
			Swap(&arr[mini], &arr[i]);
		}

	}
}

选择排序（SelectSort）总结：

基本思路：每次选出当前未排序部分的最小元素，与未排序部分的第一个元素交换。

时间复杂度：

最坏和平均时间复杂度都是 O(n²)，因为每一轮内层循环会遍历剩余的所有元素。

空间复杂度是 O(1)，因为选择排序是就地排序，不需要额外的存储空间。
展示：

方法二

c 复制代码

void SelectSort(int* arr, int n)
{  
	int left = 0;
	int right = n - 1;
	while (left < right)
	{
		int mini = left;
		int maxi = right;


		for (int i = left + 1; i <=right; i++)
		{

			if (arr[mini] > arr[i])
			{
				mini = i;
			}

			if (arr[maxi] < arr[i])
			{
				maxi = i;
			}
		}

		Swap(&arr[mini], &arr[left]);

		if (maxi == left)
		{
			maxi = mini;
		}

		Swap(&arr[maxi], &arr[right]);
		left++;
		right--;

	}
}

易错点：

c 复制代码

if (maxi == left)
		{
			maxi = mini;
		}

如果没有这段代码：

原因：
如果maxi 与 left 相同，则arr[left]与arr[mini]交换后，值发生改变，在进行maxi与right产生错误。
总结：

基本思路：每次在未排序部分中选出最小和最大值，并将其分别放到数组的两端（left 和 right）。

时间复杂度：最坏和平均情况下，时间复杂度仍为 O(n²)，因为需要通过两次遍历（内外循环）找到最小值和最大值。

快速排序

方法一（经典法）

c 复制代码

void QuickSort(int* arr, int left,int right)
{
	if (left >= right) return;
	
	int pivoti = left;

	int begin = left;
	int end = right;


	while (begin < end)
	{   
		while (begin < end && arr[end] >= arr[pivoti]) end--;
		while (begin < end && arr[begin] <= arr[pivoti]) begin++;
		Swap(&arr[begin], &arr[end]);
	}

	Swap(&arr[pivoti], &arr[begin]);
	QuickSort(arr, left, end - 1);
	QuickSort(arr, end + 1, right);
}

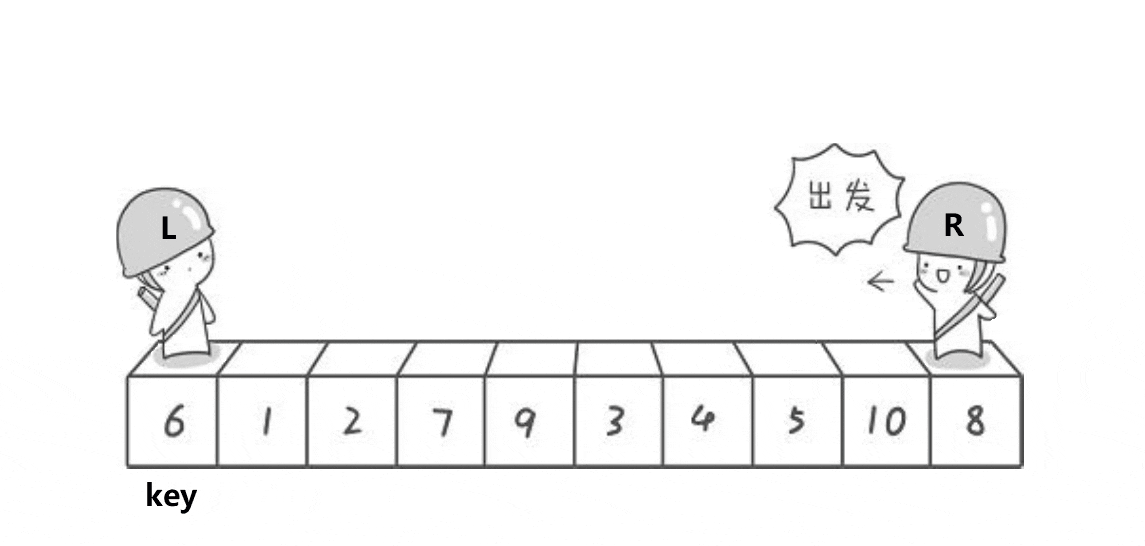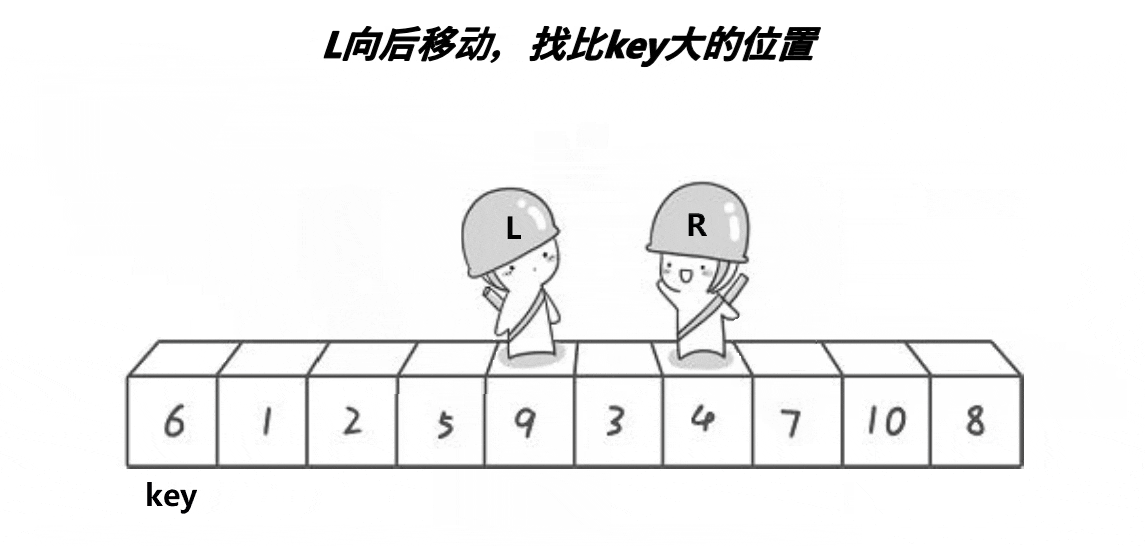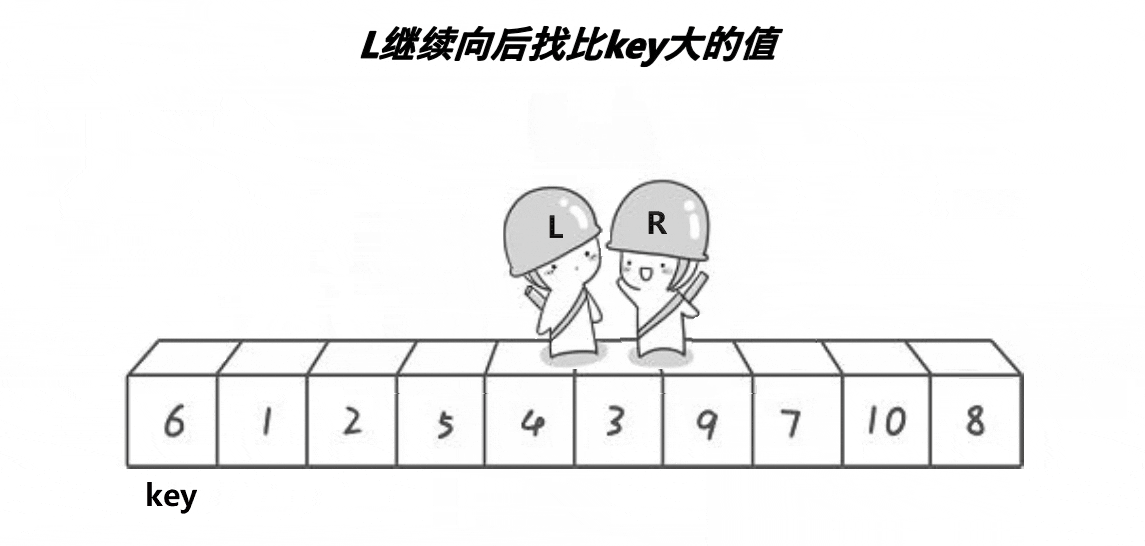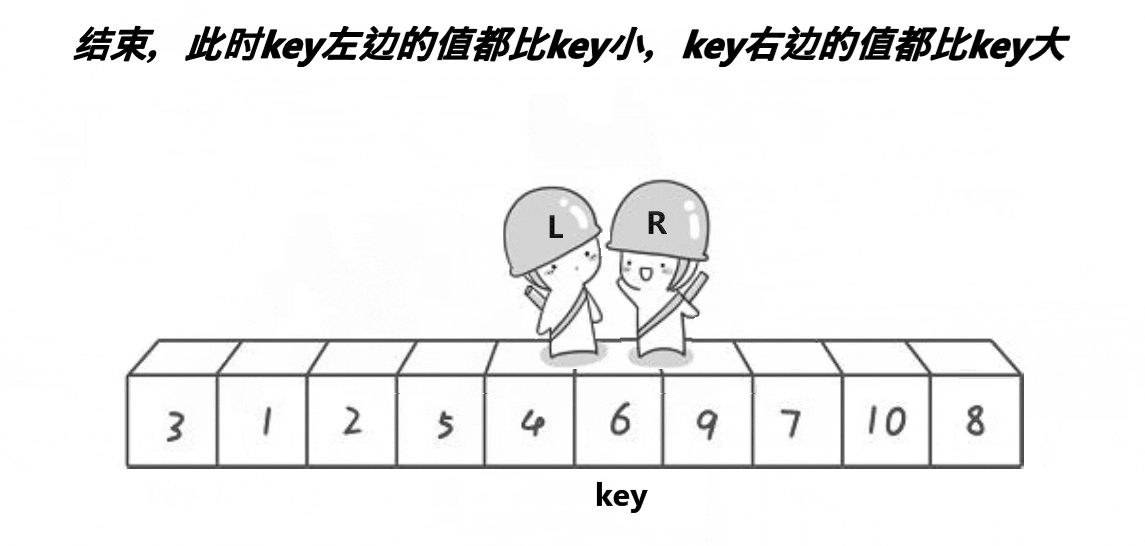
解释

1.为什么pivot为什么会找到正确排序位置？

程序扫描数组，找到比 pivot 小的元素，交换到左边；找到比 pivot 大的元素，交换到右边。

当扫描完，pivot 就处在一个位置，左边的都是小于它的，右边的都是大于它的。

这时，pivot 就被放到了正确的排序位置。

2.为什么选left，为什么先走right侧后走left侧，肯定能达到小于pivot处？

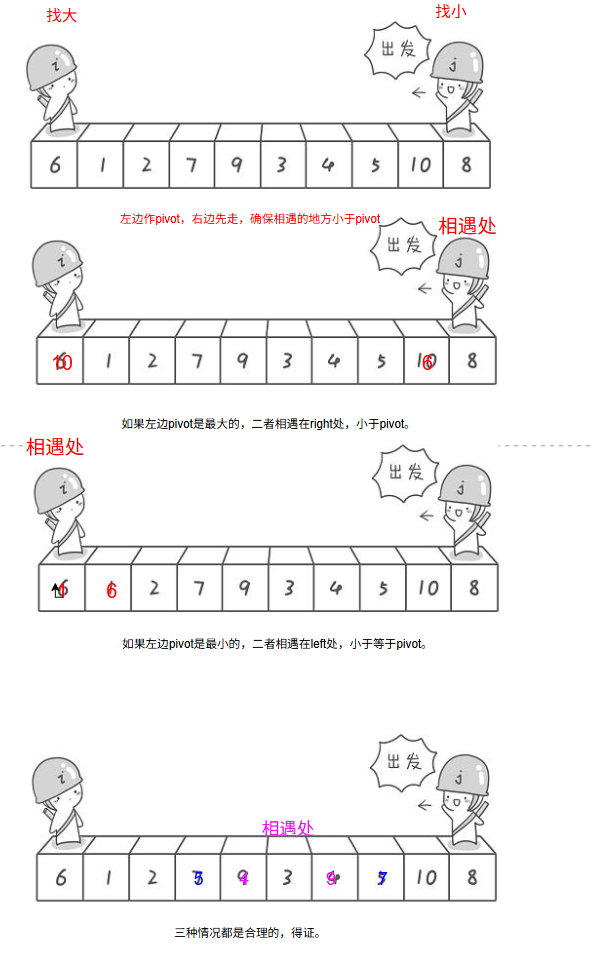
3.使用小于等于为什么可以？

这样做是为了防止在某些情况下，pivot 会被跳过。假设有相同的元素与 pivot 相等，使用 <= 会让相同的元素进入右侧（即 pivot 右边）。这样保证了数组中的所有元素都被处理，避免遗漏。
假设数组是 [5, 2, 8, 5, 7]，pivot 为 5。

如果我们用 <=，那么当 begin 扫描到第二个 5 时，它会把它放到右边，而不会停在 pivot 之前。

如果我们用 <，可能会跳过第二个 5，使得它不正确地位于 pivot 的左边。

方案二（挖洞法）

c 复制代码

void QuickSort2(int* arr, int left, int right)
{
	if (left >= right) return;
	int hole = left;
	int pivot = arr[left];

	int low = left;
	int high = right;
	while (low < high)
	{
		while (low < high && arr[high] >= pivot) high--;
		arr[hole] = arr[high];
		hole = high;

		while (low < high && arr[low] <= pivot) low++;
		arr[hole] = arr[low];
		hole = low;
	}
	arr[hole] = pivot;

	QuickSort2(arr, left, hole - 1);
	QuickSort2(arr, hole + 1, right);
}

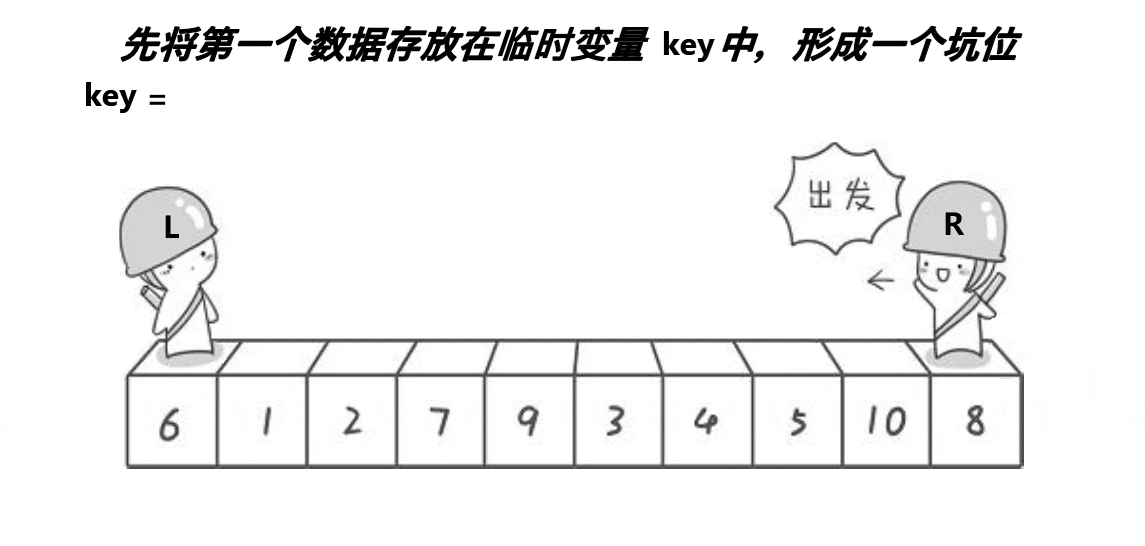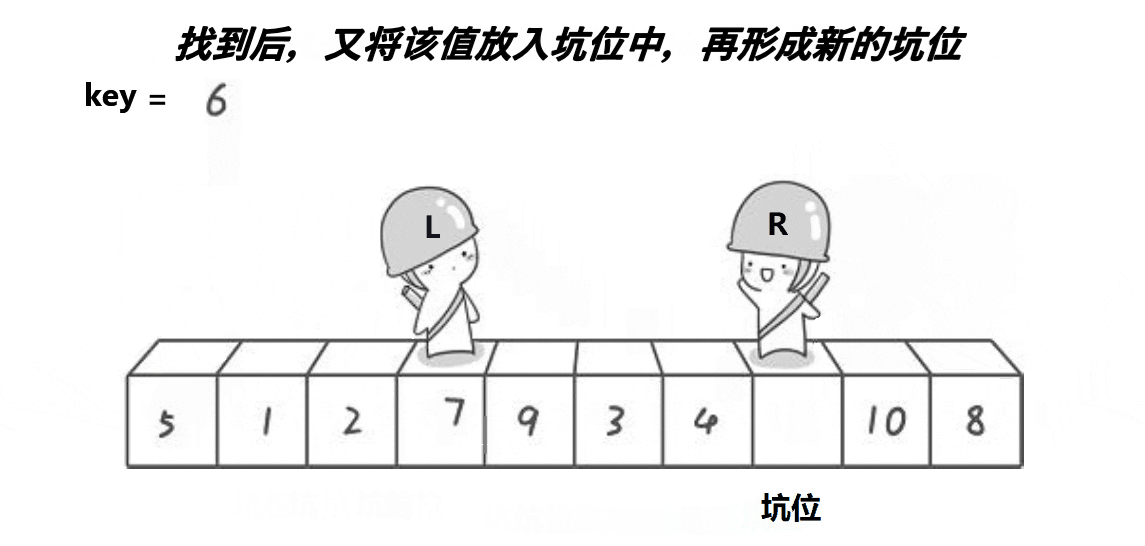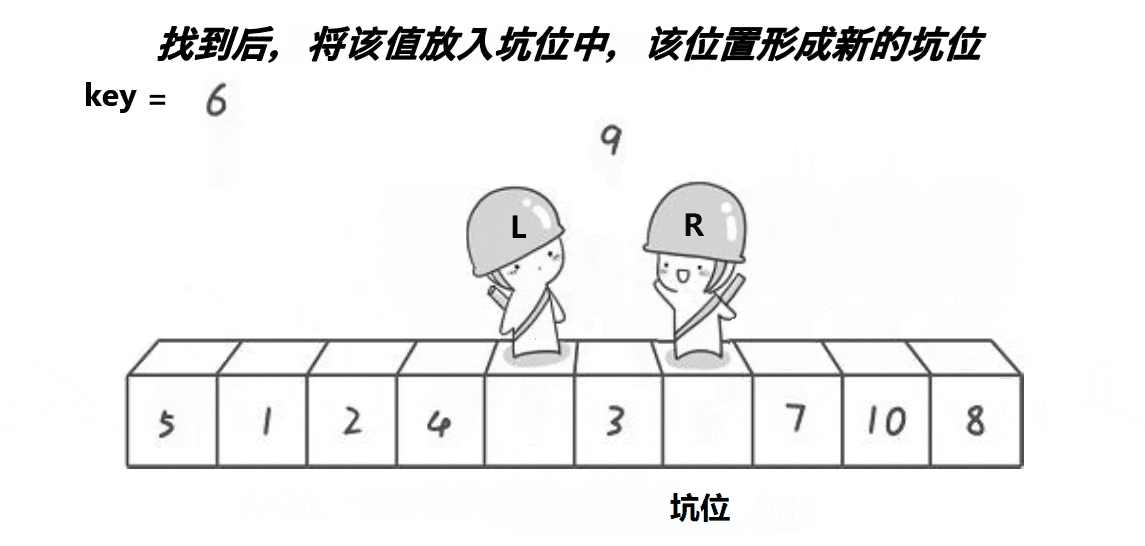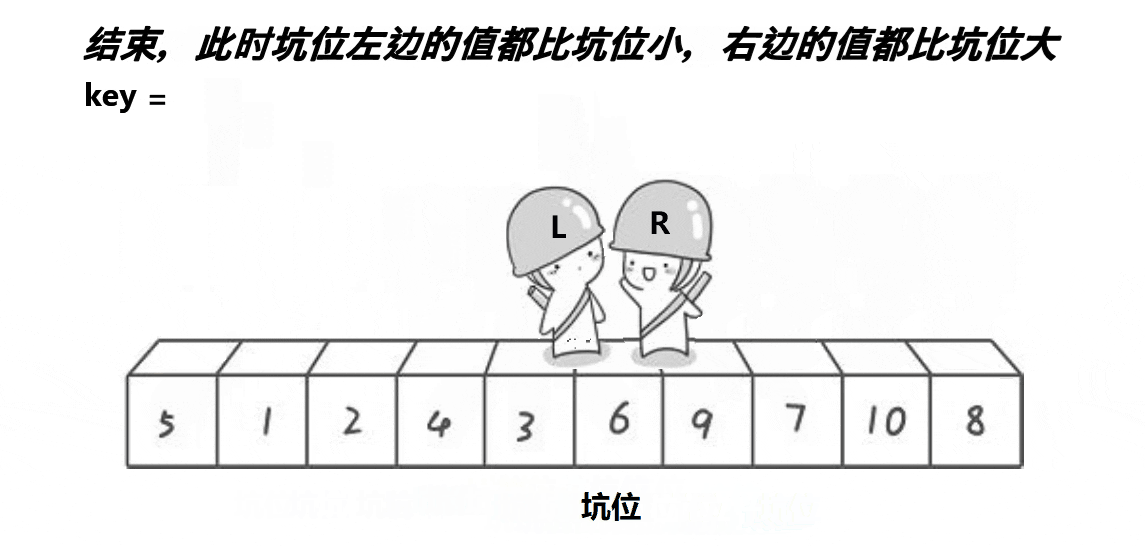
解释

c 复制代码

arr[hole] = pivot;

这一步相当于经典QuickSort中的Swap，把hole左右两边分开，一边大，一边小。

方案三（前后指针）

c 复制代码

void QuickSort3(int* arr, int left, int right)
{   
	if (left >= right)
		return;

	int midi = GetMidNumi(arr, left, right);
	if(midi != left)
	Swap(&arr[left], &arr[midi]);
	int pivoti = left;

	int prev = left;
	int cur = left + 1;
	while (cur <= right)
	{
		if (arr[cur] < arr[pivoti] && ++prev != cur)
		{
			Swap(&arr[prev], &arr[cur]);
		}
		cur++;
	}
	Swap(&arr[prev], &arr[pivoti]);

	QuickSort3(arr, left, prev - 1);
	QuickSort3(arr, prev + 1, right);
}

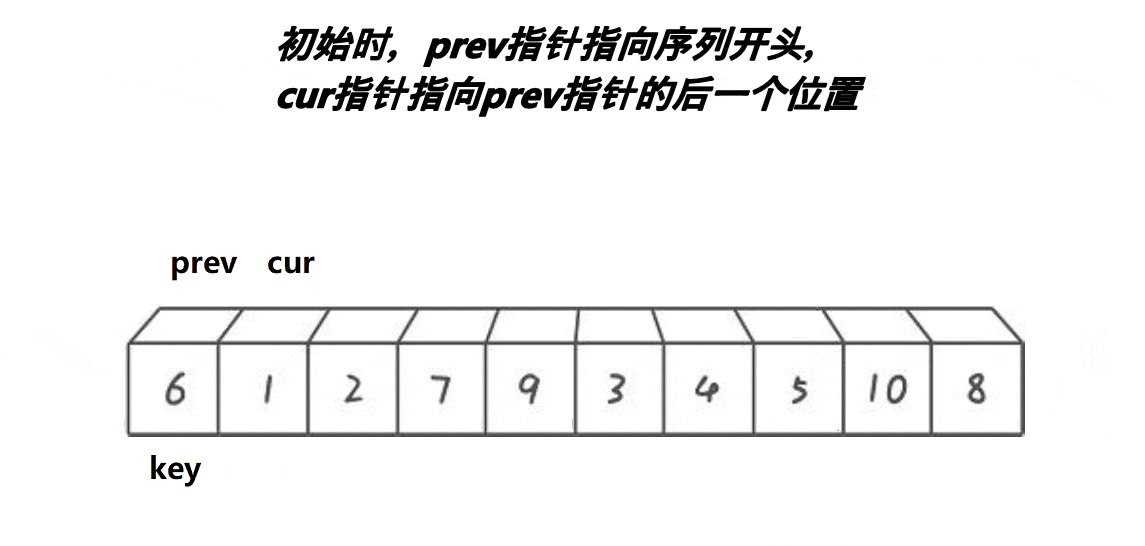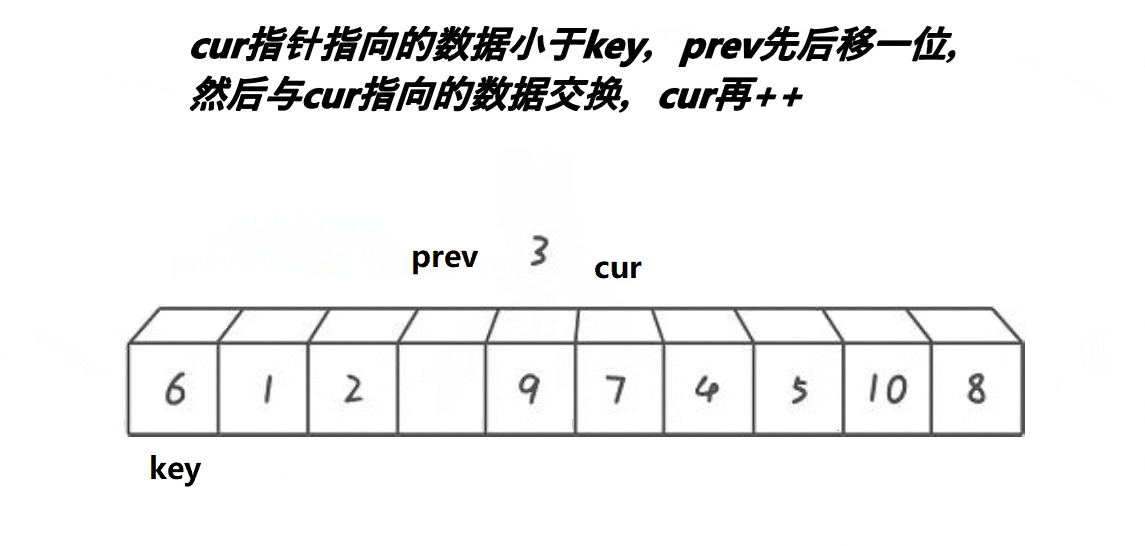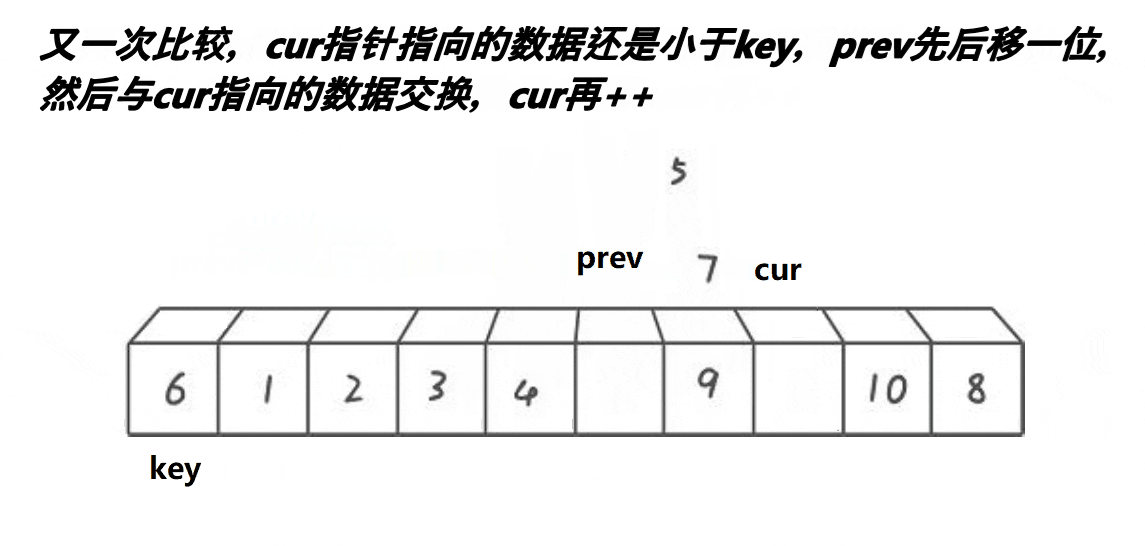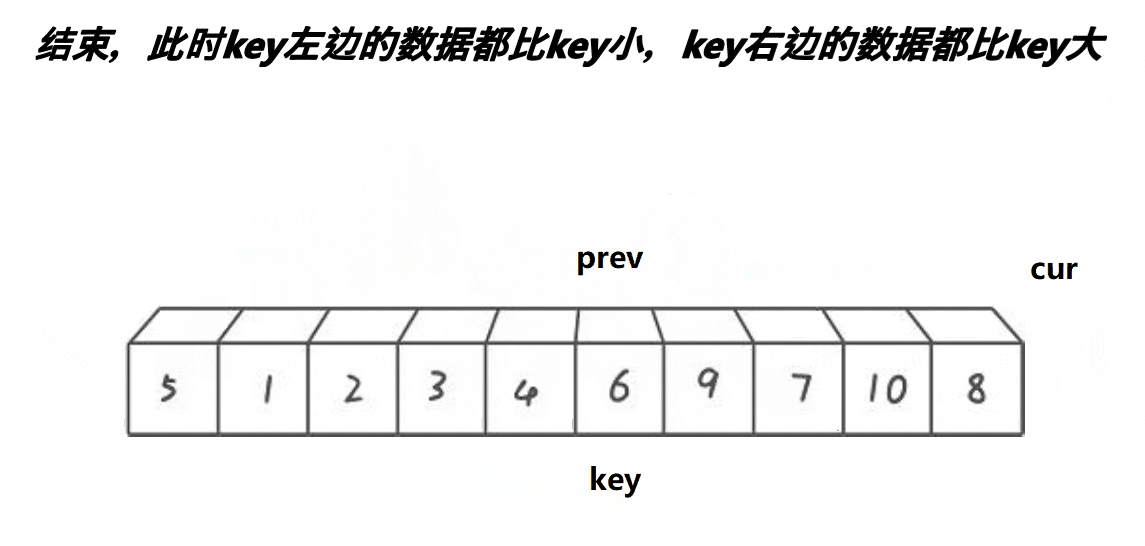
解释

c 复制代码

if (arr[cur] < arr[pivoti] && ++prev != cur)
		{
			Swap(&arr[prev], &arr[cur]);
		}
		cur++;

1.这段代码意思是如果arr[pivoti]>arr[cur],prev先++，到达下一个位置（肯定大于arr[pivoti]，且prev++不是cur，防止多个小的数连续）。

2.如果arr[pivoti]>arr[cur],只有cur++。

解释三种方案的递归部分

c 复制代码

QuickSort(arr, left, tmp - 1);  // 递归处理左边部分
QuickSort(arr, tmp + 1, right); // 递归处理右边部分

选择枢轴：首先我们选择一个枢轴 pivot，然后把数组分成两部分：

左边的部分是小于 pivot 的元素。

右边的部分是大于 pivot 的元素。

递归：对左右两部分分别再做同样的操作：

左边的部分再去选择枢轴并分成两部分，直到左边的部分只有一个元素。

右边的部分也会继续选择枢轴，直到它也只剩一个元素。

递归停止：当一个子数组只有一个元素或没有元素时，递归就停止了，因为一个元素已经是有序的了。

QuickSort总结

分治法：

分割数组：通过一个枢轴元素（pivot）将数组分成两部分，左边的部分小于枢轴，右边的部分大于枢轴。

递归排序：递归地对这两部分进行排序，直到数组完全有序。

时间复杂度：

最优情况：时间复杂度是 O(n log n)，发生在每次分割都能恰好把数组分成两等部分时。

最坏情况：时间复杂度是 O(n²)，发生在数组已经是有序的情况下，每次分割都只剩下一个元素。为了避免这种情况，通常会随机选择枢轴来优化。

pivot选取问题

方案一

c 复制代码

//取中间值
int GetMidNumber(int* arr, int left, int right)
{
	int mid = left + right / 2;

	if ((arr[mid] > arr[left] && arr[mid] < arr[right])
		|| (arr[mid] > arr[right] && arr[mid] < arr[left])) return mid;

	if ((arr[right] > arr[mid] && arr[right] < arr[left])
		|| (arr[right] > arr[left] && arr[right] < arr[mid])) return right;

	return left;

}

方案二

c 复制代码

//随机pivot
int randpivot = rand()%(right-left)+left;
Swap(&arr[left], &arr[randpivot]);
pivot = left;

解释原因

如果直接取 left 作为pivot，在以下情况下会出问题：

数据已经排序或逆序：

如果数据已经有序，取 left 会导致每次只划分一个元素，会导致取值极端化，递归层次加深，性能会变差，退化成 O(n²)。

数据全相同：

如果数组元素都相同，取 left 作为枢轴无法有效划分，递归也不会减少数组的规模，浪费时间。

举例

假如数据是 [1, 2, 3, 4, 5] 这样有序的，选 1 作为枢轴时，就会发生：

第一轮划分：选 1，它小于所有其他元素，所以它就"被迫"排到最前面了，然后剩下 [2, 3, 4, 5] 继续。

第二轮划分：然后在 [2, 3, 4, 5] 里选枢轴，选出来的可能是 2，然后剩下 [3, 4, 5]。每次划分其实就"排掉了一个元素"，其他的还要继续做排序。

总结

预告：下一篇是归并排序。