一、决策树(分类)
1. 概念
决策树是一种树形结构的分类模型,通过一系列规则(即树的分支)对数据进行分割。每个内部节点代表一个特征判断,每个分支代表判断结果,每个叶节点代表最终分类结果。
类比:就像玩"20个问题"游戏,通过不断提问缩小答案范围(例如:"是动物吗?"→"有羽毛吗?"→"是鸭子")。
2. 基于信息增益的决策树(ID3算法)
核心思想:选择能带来最大信息增益的特征作为分割标准。
-
信息熵(Entropy) :度量数据集混乱程度(不确定性)的指标。 信息熵的值越大,表示数据集的混乱程度越高(不确定性越大)。当数据集完全属于同一类别时,信息熵为0(最纯净)。计算公式为:
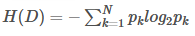
其中
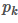
是第k类样本的比例
示例 :二分类数据集(正例50%,负例50%),熵 = - (0.5log₂0.5 + 0.5log₂0.5) = 1(最混乱) -
信息增益(Information Gain) :信息增益表示使用某个特征A进行分割后,数据集混乱程度减少的程度(即信息不确定性的减少)。计算公式为:
特征A对数据集D的信息增益 = 原熵 - 按特征A分割后的加权平均熵
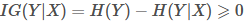
其中 ( D_v ) 是特征A取值为v的子集。 信息增益越大,说明使用该特征分割后数据越纯净。
决策原则:选择信息增益最大的特征作为当前节点
3. 基于基尼指数的决策树(CART算法)
基尼指数(Gini Index) :衡量数据不纯度(值越小越纯), 基尼指数越小,表示数据集的纯度越高。当数据集完全属于同一类别时,基尼指数为0。
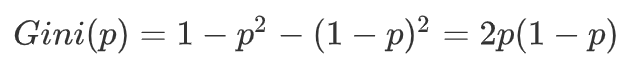
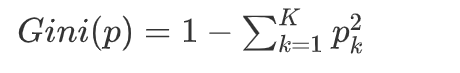
示例 :二分类(正例100%),基尼指数=1-(1²+0²)=0(最纯)
分割后基尼指数计算类似信息增益的加权平均
4. 两种方法对比
| 方法 | 特点 |
|---|---|
| 信息增益(ID3) | 倾向于选择取值多的特征 |
| 基尼指数(CART) | 计算更简单,常用作默认 |
5. 决策树建立步骤
- 计算所有特征的信息增益/基尼指数
- 选择最佳特征作为根节点
- 按特征值划分数据集
- 递归构建子树
- 终止条件:节点样本全同类/无特征可用/达最大深度
6. 决策树的优缺点
- 优点:模型直观,易于理解和解释;不需要对数据进行复杂的预处理(如归一化)。
- 缺点:容易过拟合(即过度适应训练数据,在测试数据上表现差);对数据中的噪声敏感。
7. sklearn API
python
from sklearn.tree import DecisionTreeClassifier
# criterion可选 'entropy' 或 'gini'
model = DecisionTreeClassifier(criterion='gini',max_depth=3) # 限制树深度防过拟合8. 示例:鸢尾花分类
python
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# 加载数据
iris = load_iris()
X, y = iris.data, iris.target
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# 训练决策树(基尼指数)
model = DecisionTreeClassifier(max_depth=2)
model.fit(X_train, y_train)
# 评估
accuracy = model.score(X_test, y_test) # 如0.93二、随机森林(集成学习方法)
1. 随机森林的概念
随机森林是一种集成学习算法,它通过构建多个决策树并将它们的预测结果进行组合(投票)来提高模型的准确性和鲁棒性(健壮性)。随机森林的核心思想是"三个臭皮匠,顶个诸葛亮"。
2. 算法原理
随机森林(Random Forest)是多个决策树的集成模型,核心思想:
- Bagging(自助采样):每棵决策树在训练时,使用从原始训练集中有放回地随机抽取的子集(称为自助样本集)。
- 特征随机性 :在每棵树的每个节点分裂时,随机选择一个特征子集(通常为特征总数的平方根),然后从中选择最优特征进行分裂。
通过这两种随机性,随机森林中的每棵树都各不相同,且具有较低的方差(即减少了过拟合的风险) 。 - 投票机制(预测过程):即每棵树对样本进行预测,最终选择得票最多的类别作为最终预测结果。
3. 为什么比单棵决策树更好?
- 降低方差:多棵树平均减少过拟合风险
- 增强鲁棒性:对噪声和异常值不敏感
- 处理高维数据:特征随机选择避免维度灾难
4. 数学本质
最终预测函数:( \hat{y} = \text{majority_vote}({h_t(x)}_{t=1}^T) )
其中 ( h_t ) 是第t棵树的预测,T是树的总数
5. sklearn API
python
from sklearn.ensemble import RandomForestClassifier
# n_estimators: 树的数量, max_features: 分裂时考虑的最大特征数
model = RandomForestClassifier(n_estimators=100, max_features='sqrt')6. 示例:手写数字识别
python
from sklearn.datasets import load_digits
digits = load_digits()
X, y = digits.data, digits.target
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# 训练随机森林
model = RandomForestClassifier(n_estimators=50)
model.fit(X_train, y_train)
# 评估
accuracy = model.score(X_test, y_test) # 通常 > 0.95三、线性回归
1. 什么是回归?
回归是监督学习的一种,其目标是预测一个连续值(如房价、温度、销售额等)。与分类任务(预测离散类别)不同,回归任务的输出是实数。
2. 回归 vs 分类
- 分类:预测离散类别(如猫/狗)
- 回归:预测连续数值(如房价、温度)
3. 线性回归模型
假设目标值 ( y ) 与特征 ( x ) 线性相关:
( y = w_0 + w_1 x_1 + w_2 x_2 + ... + w_n x_n )
其中:
- ( w_0 ):截距(bias)
- ( w_1,...,w_n ):特征权重(weights)
4. 损失函数(Loss Function)
为了找到最佳的权重参数,我们需要定义一个损失函数来衡量预测值与真实值之间的差异。线性回归使用均方误差(Mean Squared Error, MSE) 作为损失函数:
均方误差(MSE) :
( MSE = \frac{1}{m} \sum_{i=1}^{m} (y_i - \hat{y}_i)^2 )
其中 m 为样本数
5. 最小二乘法求解
目标 :找到权重 ( w ) 使 MSE 最小化
闭式解(解析解) :
( W = (X^T X)^{-1} X^T Y )
其中:
- ( X ):设计矩阵(每行一个样本,首列为1)
- ( Y ):目标值向量
几何解释:寻找最佳拟合直线,使所有数据点到直线的垂直距离平方和最小
6. 多参数回归
当输入特征有多个时(如房价预测中面积+房龄+位置),即扩展为多元线性回归,模型扩展为:
( y = w_0 + w_1 x_1 + w_2 x_2 + ... + w_n x_n )
7. sklearn API
python
from sklearn.linear_model import LinearRegression
model = LinearRegression() # 默认使用最小二乘法8. 示例:波士顿房价预测
python
from sklearn.datasets import fetch_california_housing # 波士顿数据集已弃用
from sklearn.metrics import mean_squared_error
housing = fetch_california_housing()
X, y = housing.data, housing.target
# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
# 训练模型
model = LinearRegression()
model.fit(X_train, y_train)
# 预测并评估
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred) # 均方误差
print("权重:", model.coef_) # 各特征权重
print("截距:", model.intercept_)算法对比总结
| 算法 | 类型 | 优势 | 局限性 | 适用场景 |
|---|---|---|---|---|
| 决策树 | 分类/回归 | 直观易解释,易可视化,无需特征缩放 | 容易过拟合 | 分类,可解释性要求高 |
| 随机森林 | 分类/回归 | 高精度,抗过拟合 | 计算开销大,可解释性差 | 分类/回归,复杂数据 |
| 线性回归 | 回归 | 计算高效,可解释性强 | 只能拟合线性关系 | 数值预测,线性关系 |