文章目录
-
-
-
- [1. 监督学习](#1. 监督学习)
- [2. 半监督学习](#2. 半监督学习)
- [3. 非监督学习](#3. 非监督学习)
-
-
1. 监督学习
- 线性回归(Linear Regression)
- 损失函数:最小二乘法(均方误差)
- 逻辑回归(Logistic Regression)
- 二分类问题
- 算法公式: P ( x ) = s i g m o d ( X W ) = 1 1 + e − ( w 1 x 1 + w 2 x 2 + . . . w k x k + 1 ) P(x) = sigmod(XW) = \frac{1}{1+e^{-(w_1x_1+w_2x_2+...w_kx_k+1)}} P(x)=sigmod(XW)=1+e−(w1x1+w2x2+...wkxk+1)1
- 损失函数:交叉熵(最大似然) P r i g h t ( x ) = p y ∗ ( 1 − p ) 1 − y = > ∏ i = 1 m p i y i ∗ ( 1 − p i ) 1 − y i P_{right}(x) = p^y*(1-p)^{1-y} => \prod_{i=1}^m{p_i^{y_i}*(1-p_i)^{1-y_i}} Pright(x)=py∗(1−p)1−y=>∏i=1mpiyi∗(1−pi)1−yi
- 决策树(Decision Tree)
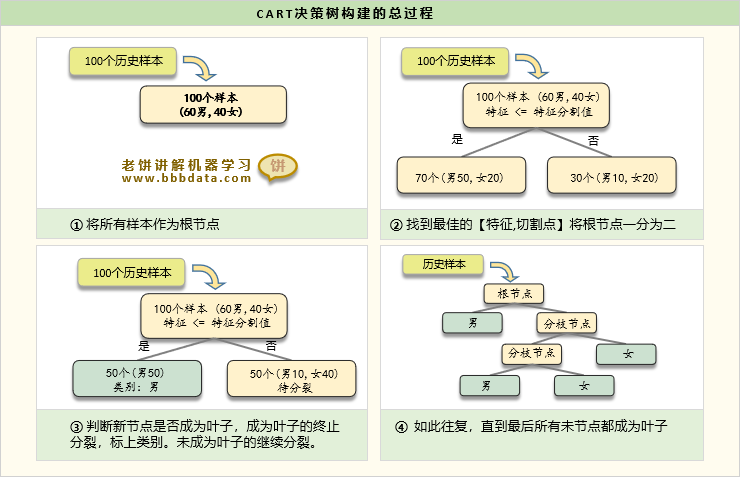
- 随机森林(Random Forest)
- 自助采样 -> 特征随机选择 -> 构建多棵决策树 -> 集成预测结果
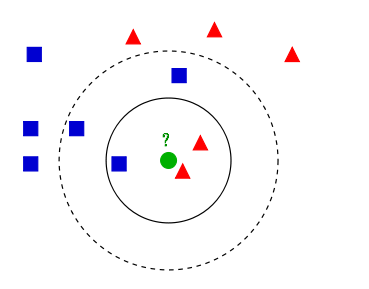
- 最近邻算法(k-NN)
- 惰性学习算法(直接用训练数据进行预测)
- 三个基本要素:距离度量(欧式距离,曼哈顿距离),K值的选择(选一个较小的值开始,分割样本交叉验证),分类决策规则
- 朴素贝叶斯(Naive Bayes)
- 分类原理(贝叶斯定理): P ( 类别 ∣ 特征 ) = P ( 类别 ) P ( 特征 ∣ 类别 ) P ( 特征 ) P(类别|特征)=\frac{P(类别)P(特征|类别)}{P(特征)} P(类别∣特征)=P(特征)P(类别)P(特征∣类别)
- 标准公式: P ( Y = C k ∣ X = x ) = P ( Y = C k ) P ( X = x ∣ Y = C k ) ∑ j = 1 n [ P ( Y = C j ) P ( X = x ∣ Y = C j ) ] P(Y=C_k|X=x)=\frac{P(Y=C_k)P(X=x|Y=C_k)}{\sum_{j=1}^n [P(Y=C_j)P(X=x|Y=C_j)]} P(Y=Ck∣X=x)=∑j=1n[P(Y=Cj)P(X=x∣Y=Cj)]P(Y=Ck)P(X=x∣Y=Ck),分母是基于特征条件独立推导的
- 引入特征独立性假设:
P ( X = x ∣ Y = C k ) = P ( X ( 1 ) = x ( 1 ) , . . . , X ( n ) = x ( n ) ∣ Y = C k ) = ∏ j = 1 n P ( X ( i ) = x ( i ) ∣ Y = C k ) P(X=x|Y=C_k)=P(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}|Y=C_k)\\ =\prod_{j=1}^n P(X^{(i)}=x^{(i)}|Y=C_k) P(X=x∣Y=Ck)=P(X(1)=x(1),...,X(n)=x(n)∣Y=Ck)=∏j=1nP(X(i)=x(i)∣Y=Ck) - 代入公式:
P ( Y = C k ∣ X = x ) = P ( Y = C k ) ∏ i = 1 n P ( X ( i ) = x ( i ) ∣ Y = C k ) ∑ j = 1 n [ P ( Y = C j ) P ( X = x ∣ Y = C j ) ] P(Y=C_k|X=x)=\frac{P(Y=C_k)\prod_{i=1}^n P(X^{(i)}=x^{(i)}|Y=C_k)}{\sum_{j=1}^n [P(Y=C_j)P(X=x|Y=C_j)]} P(Y=Ck∣X=x)=∑j=1n[P(Y=Cj)P(X=x∣Y=Cj)]P(Y=Ck)∏i=1nP(X(i)=x(i)∣Y=Ck)
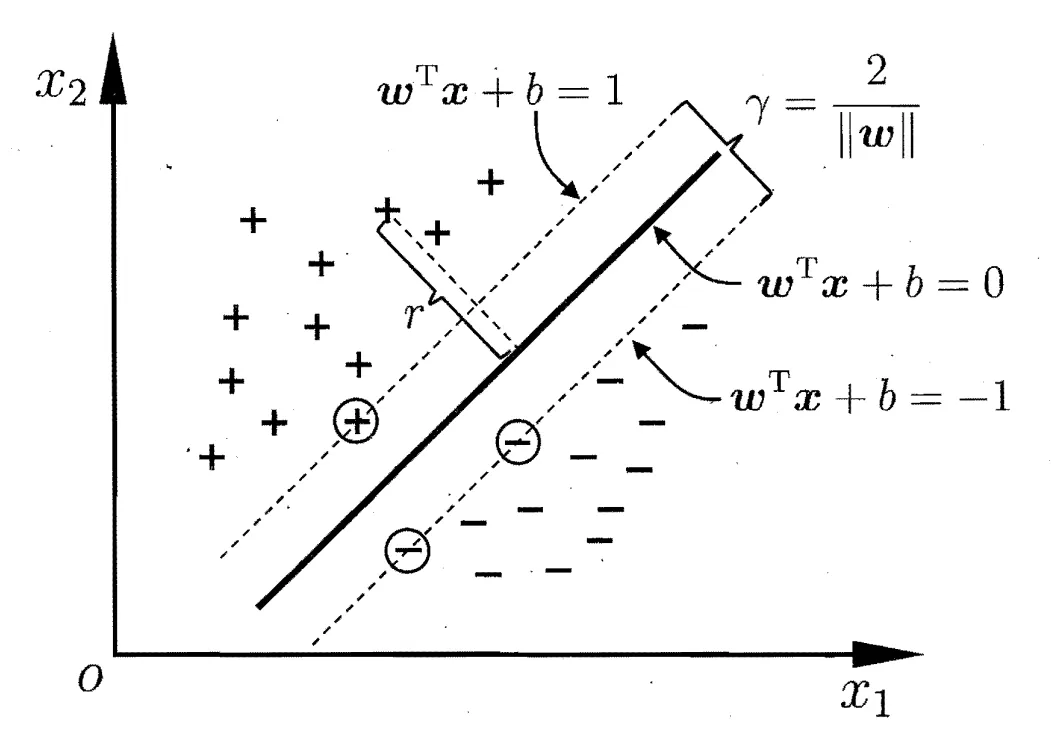
- 支持向量机(SVM)
- 二分类
- 超平面,使所有样本的距离间隔最小值最大
- 核函数:非线性可分 -> 特征空间升维
2. 半监督学习
| 算法类型 | 代表算法 | 适用场景 | 优势 |
|---|---|---|---|
| 基于图的方法 | 标签传播 (Label Propagation, LP) | 社交网络、推荐系统 | 直观,适合关系数据 |
| 生成模型 | 高斯混合模型(GMM)+ EM,变分自编码器(VAE) | 文本、图像聚类 | 概率解释性强 |
| 低密度分离 | 半监督支持向量机(S3VM) | 医疗、异常检测 | 边界清晰,抗噪声 |
| 一致性正则化 | Mean Teacher, FixMatch | 图像、语音 | 适合深度学习,鲁棒性强 |
| 伪标签 | 自训练(Self-Training), Noisy Student | 语音识别、NLP | 简单易实现 |
| 对比学习 | SimCLR | 多模态数据(图像+文本) | 无需负样本,高效表征学习 |
3. 非监督学习
- K-means 聚类(K-means Clustering)
- 重要概念:簇,质心(每次动态调整,文本距离的均值)
- 初始化 K 的大小:误差平方和 SSE + 手肘法
- 分类目标:簇内差异小(相似),簇间差异大(不相似)
- 层次聚类(Hierarchical Clustering)
- 自顶向下,自底向上
- 主成分分析(PCA)
- 降维
- 方法 :特征矩阵 旋转变换
- 自编码器(Auto-Encoders)
- 降维、特征提取
- 包含 Encoder (对原始样本进行编码) 和 Decoder (对经过编码后的向量,进行解码,从而还原原始样本)
- 文本检索
- 词袋模型 BOW,基于词频,丢失词序、语义、共现关系等高维信息
- 词嵌入模型:word2vec、GloVe、fastText,词向量固定不变,没有结合上下文信息,无法处理一词多义
- Auto-Encoder:BERT
- 图像检索:CNN
- 孤立森林(Isolation Forest)
- 异常检测算法
- 通过构建多棵 孤立树(iTree)成森林,再基于样本在森林中的表现判断异常