【力扣hot100】64. 最小路径和

一、题目

复制代码

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，
使得路径上的数字总和为最小。
说明：每次只能向下或者向右移动一步。

示例 1：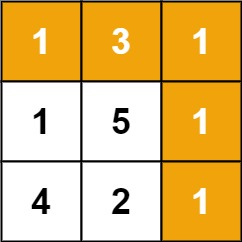

复制代码

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：
输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 200

二、思路

动态规划还是不会做，需要多写多练。思考很久无果，看了眼题解才有了思路。

在这题中，右下角的最短路径和实则就是上路径和up和左路径和left取小（只能向下或右走）。而up和left也能被切分成两个矩形，所以问题逐渐变为了在每个格子取最短路径和。

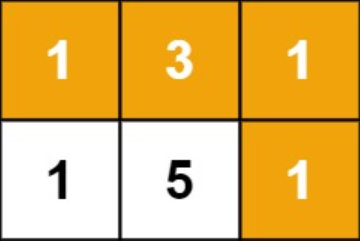
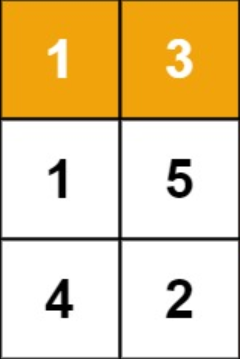
显然，左上角的三个数的最短路径都是唯一的，即1，1，3，所以以此递归就能得到每个格子的最短路径和，最后取小就可以得到右下角的最短路径和了

三、题解

cpp 复制代码

class Solution {
private:
	vector<vector<int>>mem;
public:
    int dfs(vector<vector<int>>&grid,int x,int y){
		if(x>=grid[0].size()||y>=grid.size()||x<0||y<0){
			return INT_MAX;    //超出区间直接返回最大值，使其排除（即取另一条路径）
		}
		if(x==0&&y==0) return mem[0][0]=grid[0][0];
		if(mem[y][x]!=-1) return mem[y][x];    //已经计算过的直接取值
		else {
			int up=dfs(grid,x,y-1);
			int left=dfs(grid,x-1,y);
			return mem[y][x]=min(up,left)+grid[y][x];    //左上路径取小
		}
	}

    int minPathSum(vector<vector<int>>& grid) {
        mem=vector<vector<int>>(grid.size(),vector<int>(grid[0].size(),-1));
		return dfs(grid,grid[0].size()-1,grid.size()-1);
    }
};