动态规划的第五篇博客!今天讲完全背包,排列组合的理解!
对于上一篇博客的494题,我之前的理解存在误区,更正的理解在本篇博客518题后续的对于递推公式理解的补充
完全背包
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
在下面的讲解中,我拿下面数据举例子:背包最大重量为4,物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
- 确定dp数组以及下标的含义
因为有两个维度需要分别表示:物品 和 背包容量
dp[i][j] 表示从下标为[0-i]的物品,每个物品可以取无限次,放进容量为j的背包,价值总和最大是多少。
- 确定递推公式
求取 dp[1][4] 有两种情况:
- 放物品1
- 还是不放物品1
如果不放物品1, 那么背包的价值应该是 dp[0][4] 即 容量为4的背包,只放物品0的情况。
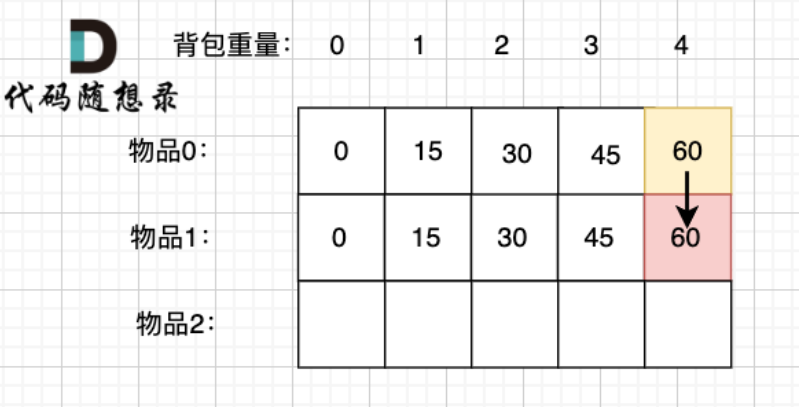
而在完全背包中,物品是可以放无限个,所以 即使空出物品1空间重量,那背包中也可能还有物品1,所以此时我们依然考虑放 物品0 和 物品1 的最大价值即: dp[1][1], 而不是 dp[0][1]
所以 放物品1 的情况 = dp[1][1] + 物品1 的价值,推导方向如图:
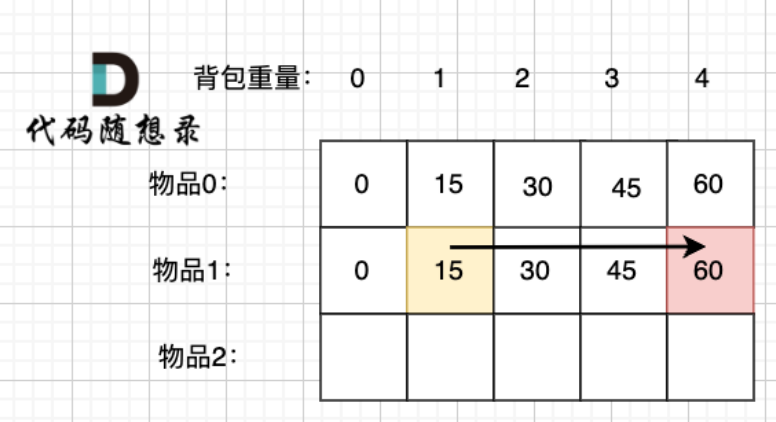
以上过程,抽象化如下:
-
不放物品i:背包容量为j,里面不放物品i的最大价值是dp[i - 1][j]。
-
放物品i:背包空出物品i的容量后,背包容量为j - weight[i],dp[i][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值,那么dp[i][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
递推公式: dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
- dp数组如何初始化
首先从dp[i][j]的定义出发,如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。如图:
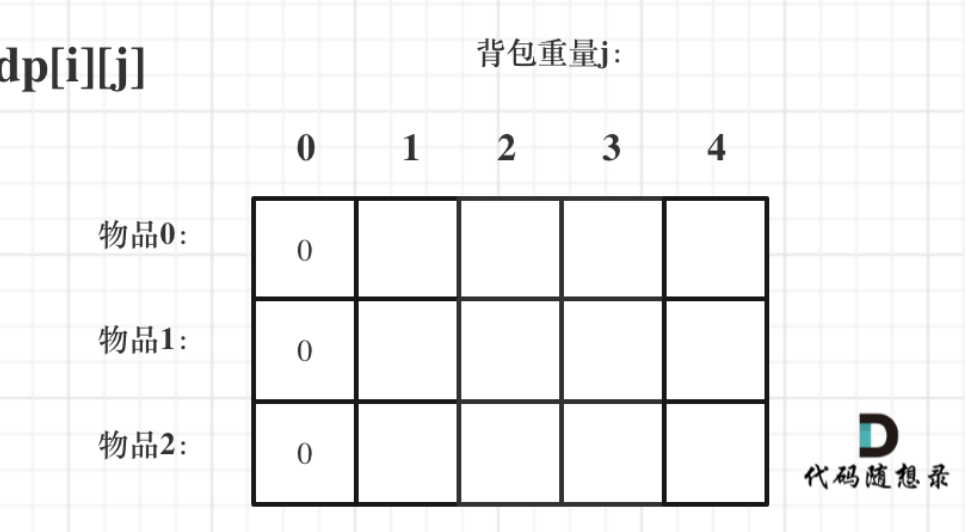
dp[0][j],即:存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。当j >= weight[0]时,dp[0][j] 如果能放下weight[0]的话,就一直装,每一种物品有无限个。
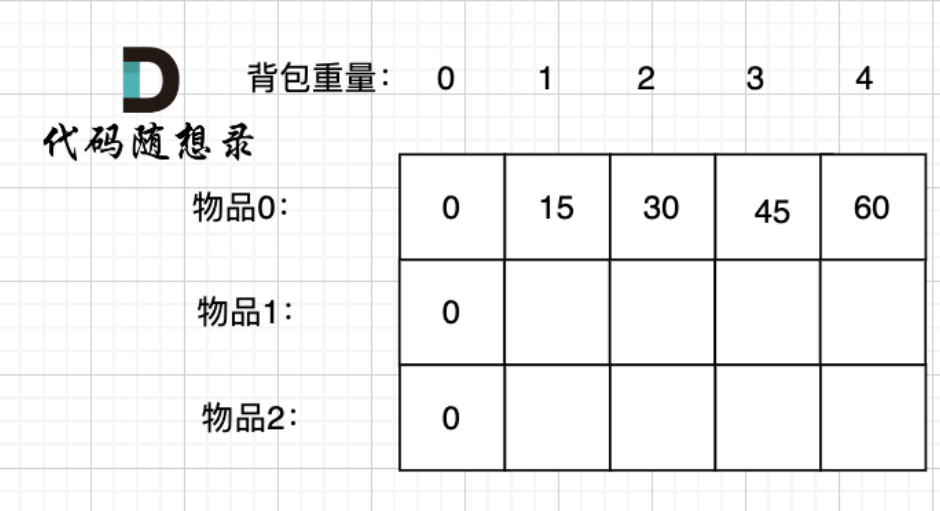
- 确定遍历顺序
都可以,先遍历物品再遍历背包更好理解一些
- 举例推导dp数组
略
python
def knapsack(n, bag_weight, weight, value):
# n 行 (物品种类)
# bag_weight (行李总重量)
# weight (单个物品重量)
# value (单个物品价值)
dp = [[0] * (bag_weight + 1) for _ in range(n)]
# 行宽列宽要注意
# 初始化 很巧妙的方法, 通过其他的位置来赋值
for j in range(weight[0], bag_weight + 1):
dp[0][j] = dp[0][j - weight[0]] + value[0]
# 动态规划
for i in range(1, n):
for j in range(bag_weight + 1):
if j < weight[i]:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])
return dp[n - 1][bag_weight]
# 输入
n, bag_weight = map(int, input().split())
weight = []
value = []
for _ in range(n):
w, v = map(int, input().split())
weight.append(w)
value.append(v)
# 输出结果
print(knapsack(n, bag_weight, weight, value))完全背包的一维理解
遍历物品 在外层 循环,遍历背包 容量在内层循环,状态如图:
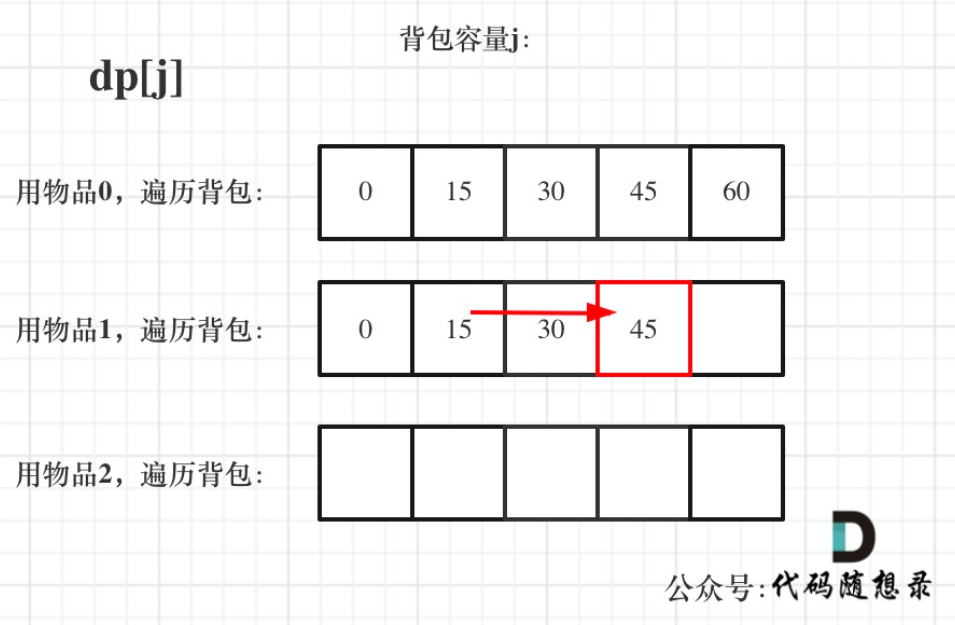
遍历背包 容量在外层 循环,遍历物品 在内层循环,状态如图:
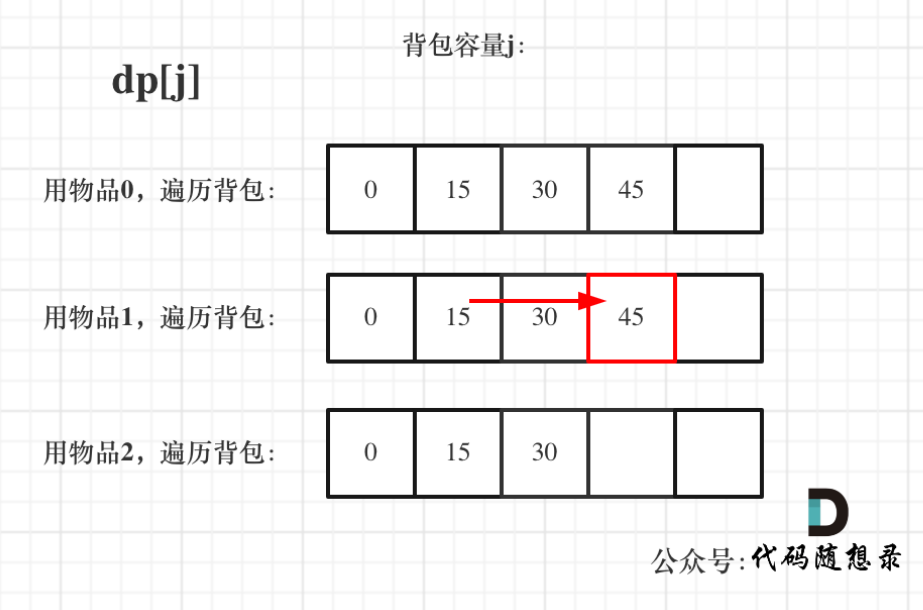
对于纯完全背包问题,其for循环的先后循环是可以颠倒的!
但如果题目稍稍有点变化,就会体现在遍历顺序上。
下列代码实现使用先遍历背包的方式,在上图中体现为纵向实现,和之前的01背包的1维数组的实现存在差别!
python
def complete_knapsack(N, bag_weight, weight, value):
dp = [0] * (bag_weight + 1)
for j in range(bag_weight + 1): # 遍历背包容量
for i in range(len(weight)): # 遍历物品
if j >= weight[i]:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
return dp[bag_weight]
# 输入
N, bag_weight = map(int, input().split())
weight = []
value = []
for _ in range(N):
w, v = map(int, input().split())
weight.append(w)
value.append(v)
# 输出结果
print(complete_knapsack(N, bag_weight, weight, value))518. 零钱兑换 II
我感觉这个类似于组合问题了,类似这种题目:给出一个总数,一些物品,问能否凑成这个总数。这是典型的背包问题!
但本题和纯完全背包不一样,纯完全背包是凑成背包最大价值是多少,而本题是要求凑成总金额的物品组合个数!
- 确定dp数组以及下标的含义
定义二维dp数值 dp[i][j]:使用 下标为[0, i]的coins[i]能够凑满j(包括j)这么大容量的包,有dp[i][j]种组合方法。
- 确定递推公式(后续补充)
所以本题递推公式:dp[i][j] = dp[i - 1][j] + dp[i][j - nums[i]
两点理解1.对于目标和求组合逻辑的理解2.对于完全背包的理解
- dp数组如何初始化
那么二维数组的最上行 和 最左列一定要初始化,这是递推公式推导的基础,dp[i][0] 都初始化为1
- 确定遍历顺序
二维DP数组的完全背包的两个for循环先后顺序是无所谓的(组合问题)。先遍历背包,还是先遍历物品都是可以的。
python
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
dp = [0]*(amount + 1)
dp[0] = 1
# 遍历物品
for i in range(len(coins)):
# 遍历背包
for j in range(coins[i], amount + 1):
dp[j] += dp[j - coins[i]]
# 回归dp数组的本身含义
return dp[amount]对于上题递推公式的补充
494. 目标和 - 力扣(LeetCode)全1背景↓:
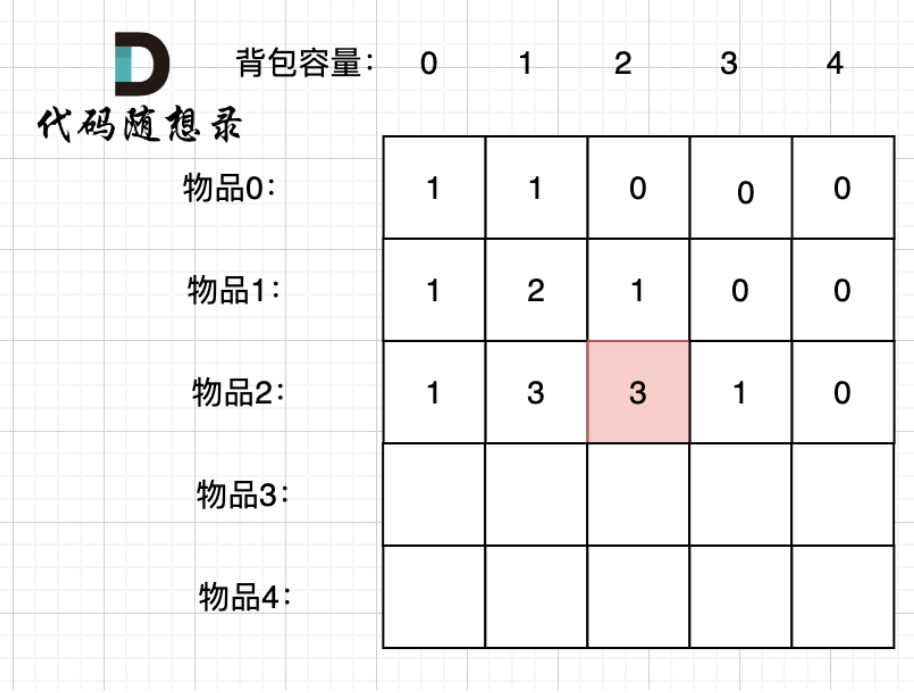
- 容量为2 的背包,如果不放 物品2 有几种方法呢?
就是3上面的1
- 容量为2 的背包, 如果放 物品2 有几种方法呢?
就是3上面一行,-num[i]的数值,因为会加物品2
抽象出来就是:
-
不放物品i:即背包容量为j,里面不放物品i,装满有dp[i - 1][j]中方法。
-
放物品i: 即:先空出物品i的容量,背包容量为(j - 物品i容量),放满背包有 dp[i - 1][j - 物品i容量] 种方法。
本题中,物品i的容量是nums[i],价值也是nums[i]。
递推公式:dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
377. 组合总和 Ⅳ
本题题目描述说是求组合,但又说是可以元素相同顺序不同的组合算两个组合,其实就是求排列!(如果本题要把排列都列出来的话,只能使用回溯算法爆搜。
- 确定dp数组以及下标的含义
dp[i]: 凑成目标正整数为i的排列个数为dp[i]
- 确定递推公式
递推公式一般都是dp[i] += dp[i - nums[j]];
- dp数组如何初始化
因为递推公式dp[i] += dp[i - nums[j]]的缘故,dp[0]要初始化为1,这样递归其他dp[i]的时候才会有数值基础。
- 确定遍历顺序
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
如果把遍历nums(物品)放在外循环,遍历target的作为内循环的话,举一个例子:计算dp[4]的时候,结果集只有 {1,3} 这样的集合,不会有{3,1}这样的集合,因为nums遍历放在外层,3只能出现在1后面!
所以本题遍历顺序最终遍历顺序:target(背包)放在外循环,将nums(物品)放在内循环,内循环从前到后遍历。
python
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
dp = [0] * (target + 1)
dp[0] = 1
for i in range(1, target + 1): # 遍历背包
for j in range(len(nums)): # 遍历物品
if i - nums[j] >= 0:
dp[i] += dp[i - nums[j]]
return dp[target]70. 爬楼梯 (进阶)
这其实是一个完全背包问题。1阶,2阶,.... m阶就是物品,楼顶就是背包。每一阶可以重复使用,例如跳了1阶,还可以继续跳1阶。
- 确定dp数组以及下标的含义
dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法。
- 确定递推公式
求装满背包有几种方法,递推公式一般都是dp[i] += dp[i - nums[j]];本题呢,dp[i]有几种来源,dp[i - 1],dp[i - 2],dp[i - 3] 等等,即:dp[i - j]
那么递推公式为:dp[i] += dp[i - j]
- dp数组如何初始化
既然递归公式是 dp[i] += dp[i - j],那么dp[0] 一定为1,dp[0]是递归中一切数值的基础所在,如果dp[0]是0的话,其他数值都是0了。
- 确定遍历顺序
这是背包里求排列问题,即:**1、2 步 和 2、1 步都是上三个台阶,但是这两种方法不一样!**所以需将target放在外循环,将nums放在内循环。
每一步可以走多次,这是完全背包,内循环需要从前向后遍历。
python
def climbing_stairs(n,m):
dp = [0]*(n+1) # 背包总容量
dp[0] = 1
# 排列题,注意循环顺序,背包在外物品在内
for j in range(1,n+1):
for i in range(1,m+1):
if j>=i:
dp[j] += dp[j-i] # 这里i就是重量而非index
return dp[n]
if __name__ == '__main__':
n,m = list(map(int,input().split(' ')))
print(climbing_stairs(n,m))