Educational Codeforces Round 181 (Rated for Div. 2) A-C

A. Difficult Contest

题目大意

给你一个串，要求串内不能出现FFT或者NTT

思路

提取出串内所有的T,放在最前面

cpp 复制代码

// Author: zengyz
// 2025-08-02 14:43

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

void solve()
{
  string s;
  cin >> s;
  int count = 0;
  for (int i = 0; i < s.size(); i++)
    if (s[i] == 'T')
      count++;
  while (count--)
    cout << "T";
  for (int i = 0; i < s.size(); i++)
  {
    if (s[i] == 'T')
      continue;
    cout << s[i];
  }
  cout << endl;
  return;
}

int main()
{
  ios::sync_with_stdio(0);
  cin.tie(0), cout.tie(0);
  int _T = 1;
  cin >> _T;
  while (_T--)
  {
    solve();
  }
  return 0;
}

B. Left and Down

题目大意

给你a,b，期望从点(a,b) 移动到终点(0,0)

每次可以选择一个不超过k大小的dx和Dy

并移动到(a-dx,b-dy)处

可以进行如下两个操作：

如果(dx,dy)第一次出现，花费为1

如果(dx,dy)重复出现，则不花费

问最少花费为多少

思路

先对其求gcd,设其gcd为tmp,且(a,b)可以由(a/tmp和b/tmp)重复tmp次获得

如果(a/tmp和b/tmp)均小于等于k,那么可以由tmp次(a/tmp和b/tmp)

花费为1

否则花费为2

cpp 复制代码

// Author: zengyz
// 2025-08-02 14:56

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

ll gcd(ll a, ll b)
{
  return b ? gcd(b, a % b) : a;
}
void solve()
{
  ll a, b, k;
  cin >> a >> b >> k;
  ll tmp = gcd(a, b);
  a /= tmp, b /= tmp;

  ll maxx = max(a, b);
  if (maxx <= k)

    cout << 1 << endl;
  else
    cout << 2 << endl;
  return;
}

int main()
{
  ios::sync_with_stdio(0);
  cin.tie(0), cout.tie(0);
  int _T = 1;
  cin >> _T;
  while (_T--)
  {
    solve();
  }
  return 0;
}

C. Count Good Numbers

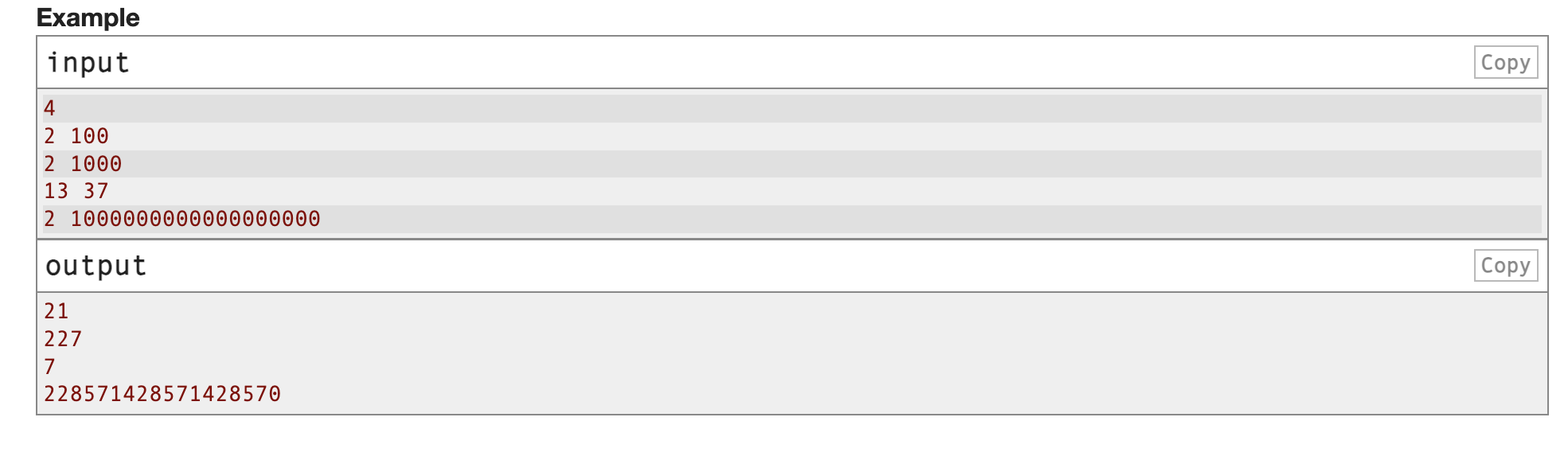
题目大意

我们称一个数为好的如果他的因式分解中所有的素数都至少有两位（大于等于10）

问在l到r之间有多少个这样的数

思路

10以下的素数只有2、3、5、7，考虑容斥原理去除所有包含2,3,5,7的数即可

cpp 复制代码

// Author: zengyz
// 2025-08-02 15:26

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

void solve()
{
  ll l, r;
  cin >> l >> r;
  auto calc = [&](ll x) -> ll
  {
    ll tmp = 0;
    tmp -= x / 2;
    tmp -= x / 3;
    tmp -= x / 5;
    tmp -= x / 7;
    tmp += x / 6;
    tmp += x / 10;
    tmp += x / 14;
    tmp += x / 15;
    tmp += x / 21;
    tmp += x / 35;
    tmp -= x / 30;
    tmp -= x / 42;
    tmp -= x / 70;
    tmp -= x / 105;
    tmp += x / 210;
    return tmp;
  };
  cout << r - l + 1 + calc(r) - calc(l - 1) << endl;
}

int main()
{
  ios::sync_with_stdio(0);
  cin.tie(0), cout.tie(0);
  int _T = 1;
  cin >> _T;
  while (_T--)
  {
    solve();
  }
  return 0;
}