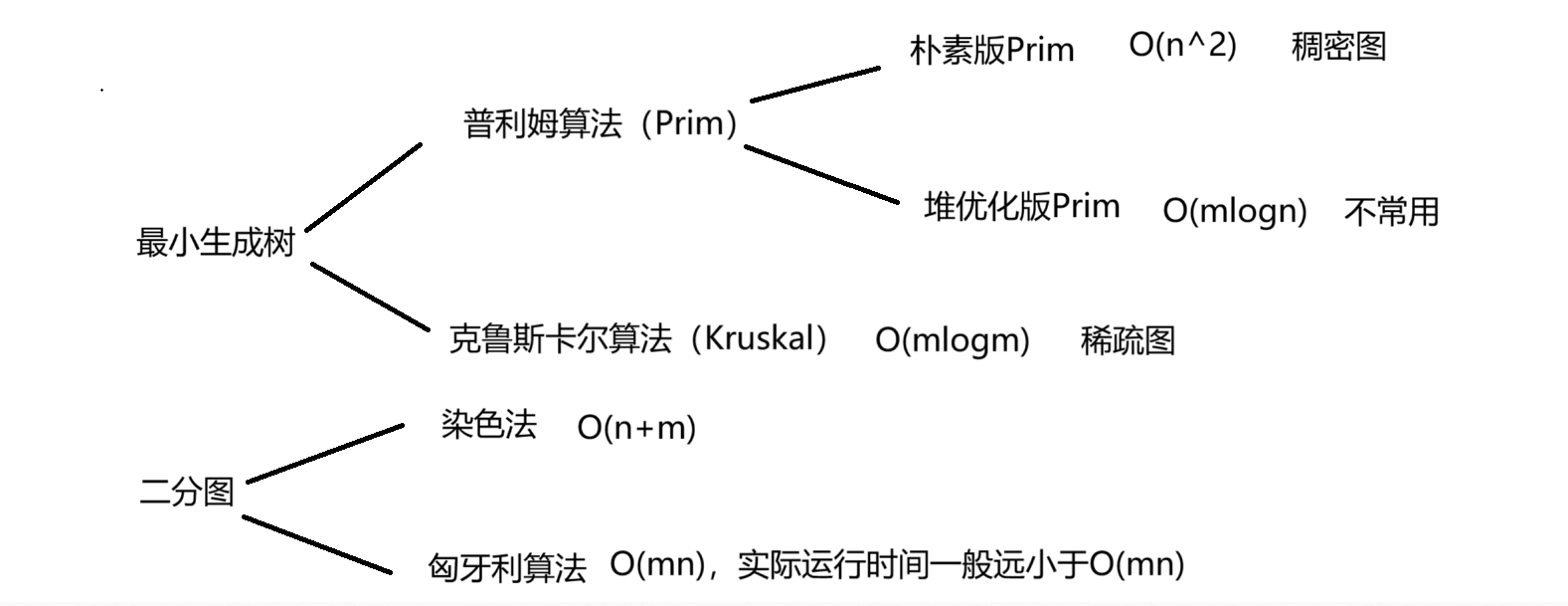
一.最小生成树
(1)朴素Prim
思路:
从任意顶点开始,逐步贪心选择当前可达的、权值最小的边,将新顶点加入生成树,直到所有顶点都被包含(或确定无法继续扩展)。
记录每个顶点到生成树的最小距离 dist[],初始时起点 dist[0] = 0,其余为 +∞。
记录顶点是否已加入生成树 st[](st[i] = true 表示已加入)。
每次从未加入树 的顶点中,选 dist[] 最小的顶点 u。
将 u 加入生成树(st[u] = true),累加其 dist[u] 到总权重
用 u 连接的所有边更新其他未加入树的顶点的 dist[]:
若边 u-v 的权值 w 小于 dist[v],则 dist[v] = w
题目
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环,边权可能为负数。求最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
给定一张边带权的无向图 G = (V, E),其中 V 表示图中点的集合,E 表示图中边的集合,n = |V|,m = |E|。由 V 中的全部 n 个顶点和 E 中 n - 1 条边构成的无向连通子图被称为 G 的一棵生成树,其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含三个整数 u、v、w,表示点 u 和点 v 之间存在一条权值为 w 的边。
输出格式
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出 impossible。
数据范围
1 ≤ n ≤ 500
1 ≤ m ≤ 10⁵
图中涉及边的边权的绝对值均不超过 10000
输入样例
cpp
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4输出样例
cpp
6代码实现
cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int P = 1e9+7;
const int N = 1e3+10;
const int INF = 0x3f3f3f3f;
int n,m;
int g[N][N];//邻接矩阵存稠密图
int dist[N];//存的是i点到集合的最短距离
bool st[N];//记录i点有没有加入树中
int prim()
{
memset(dist,0x3f,sizeof dist);//把所有点到集合的距离初始化为正无穷
int res = 0;//记录最小生成树所有边的长度之和
for(int i = 0;i<n;i++)
{
int t = -1;
for(int j = 1;j<=n;j++)
{
//如果j点还没有在集合里 && j是到集合距离最短的点
if(!st[j]&&(t==-1||dist[t]>dist[j])) t = j;
}
if(i&&dist[t]==INF) return INF;//如果不是第一个点并且当前点到集合的距离是无穷,说明图不连通
if(i) res += dist[t];//如果不是第一个点,说明dist[t]是把集合外一点加入树的最小代价
//注意要把更新放到加入的后面,以免出现自环并且g[t][t]是负数的情况
for(int j = 1;j<=n;j++) dist[j] = min(dist[j],g[t][j]);//更新其他点到集合的最小长度
st[t] = true;//加到树中
}
return res;
}
int main()
{
cin>>n>>m;
memset(g,0x3f,sizeof g);
while(m--)
{
int a,b,c;cin>>a>>b>>c;
g[a][b] = min(g[a][b],c);
g[b][a] = min(g[b][a],c);
}
int ans = prim();
if(ans==INF) cout<<"impossilbe"<<endl;
else cout<<ans<<endl;
return 0;
}
(2)Kruskal
思路:
1.先将所有边按权重从小到大排序 O(mlogm)
2.从小到大枚举每条边 a,b,权重为c,如果a,b不连通,将这条边加入集合 ,可以用并查集实现O(m)
代码实现
cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int P = 1e9+7;
const int N = 2e5+10;
const int INF = 0x3f3f3f3f;
int n,m;
int p[N];
struct node
{
int a,b,w;
bool operator<(const node &W) const
{
return w<W.w;
}
}edges[N];
int find(int x)//并查集模板
{
if(p[x]!=x) p[x] = find(p[x]);
return p[x];
}
int main()
{
cin>>n>>m;
for(int i = 0;i<m;i++)
{
int a,b,w;cin>>a>>b>>w;
edges[i] = {a,b,w};
}
sort(edges,edges+m);//把所有边从小到大排序
for(int i = 1;i<=n;i++) p[i] = i;//初始化并查集
int res = 0,cnt = 0;//res存的是最小生成树当中所有树边的权重之和
//cnt存的是当前加入了多少条边
for(int i = 0;i<m;i++)
{
int a = edges[i].a,b = edges[i].b,w = edges[i].w;
a = find(a),b = find(b);
if(a!=b)
{
p[a] = b;//把a和b加入到同一连通图中,并查集思想
res += w;
cnt++;
}
}
if(cnt<n-1) cout<<"impossible"<<endl;
else cout<<res<<endl;
return 0;
}
二.二分图
(1)染色法
图的性质:一个图是二分图当且仅当图中不含奇数环
基于染色:一个无向图 G=(V,E) 是二分图,当且仅当可以用两种颜色对图中的所有顶点进行染色,使得任意相邻的两个顶点颜色都不同。如果无法用两种颜色进行这样的染色,那么该图就不是二分图
所以利用染色法来判断一个图是不是二分图,如果在染色过程中有矛盾产生,那么就不是二分图,反之是二分图。
题目
给定一个 n 个点 m 条边的无向图,图中可能存在重边和自环。请你判断这个图是否是二分图。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行,每行包含两个整数 u 和 v,表示点 u 和点 v 之间存在一条边。
输出格式
如果给定图是二分图,则输出 Yes,否则输出 No。
数据范围
1≤n,m≤1e5
输入样例
cpp
4 4
1 3
1 4
2 3
2 4输出样例
cpp
Yes代码实现
cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int P = 1e9+7;
const int N = 2e5+10;
const int INF = 0x3f3f3f3f;
int n,m;
int h[N],e[N],ne[N],idx;
int color[N];
bool dfs(int u,int c)
{
color[u] = c;
for(int i = h[u];i!=-1;i = ne[i])
{
int j = e[i];
if(!color[j]) //如果下一个点没有染色
{
if(!dfs(j,3-c)) return false;//相邻点染成另一种颜色
}
else if(color[j]==c) return false;//如果染色,判断是否有矛盾,即相邻两点颜色相同
}
return true;
}
void add(int a,int b)//存图
{
e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}
int main()
{
cin>>n>>m;
memset(h,-1,sizeof h);
while(m--)
{
int a,b;cin>>a>>b;
add(a,b);
add(b,a);
}
bool flag = true;//记录染色过程中是否有矛盾
for(int i = 1;i<=n;i++)
{
if(color[i]==0)
{
if(!dfs(i,1))//如果一个点没有被染色,那么将其染成1,往下深度遍历
{
flag = false;
break;
}
}
}
if(flag) puts("Yes");
else puts("No");
return 0;
}
(2)匈牙利算法
可以理解为男女匹配 y总的方法hh(仅供理解题目)
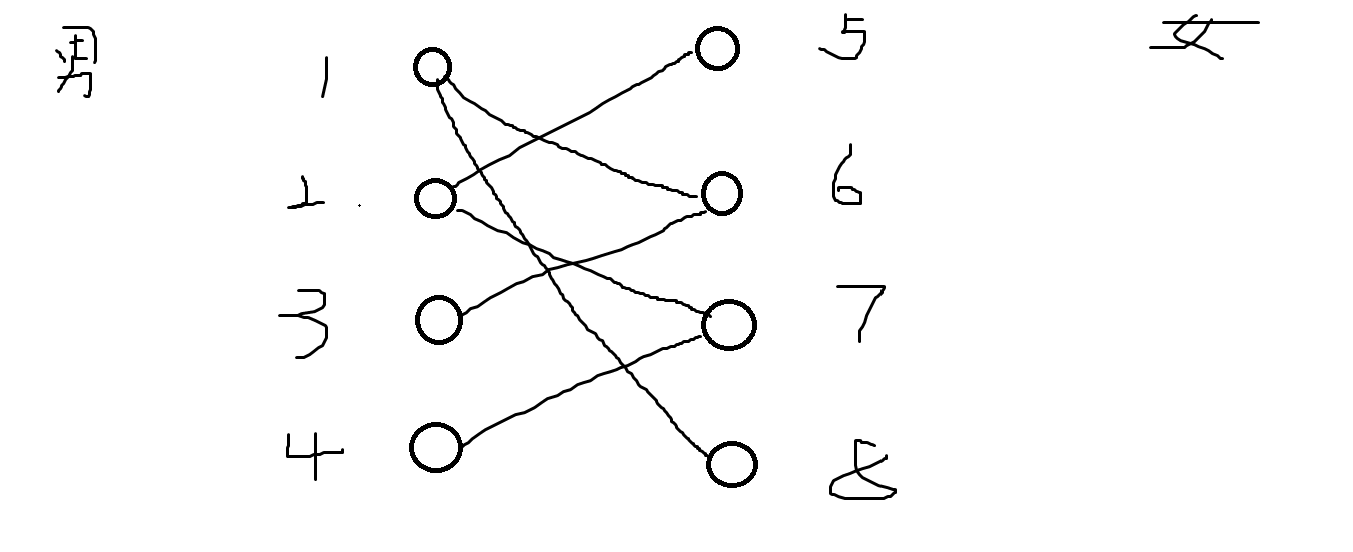
遍历所有男生
从第一个男生开始,找到和他连接的女生,比如6号,此时6号还没有与之匹配的男生,那么1号和6号匹配成功。
第二个男生找和他连接的女生,比如5号,此时5号也没有与之匹配的男生,那么2号和5号匹配成功。
第三个男生找和他连接的女生,比如6号,但是6号已经匹配,那么找与六号匹配的男生,是1号。再看1号能不能换一个女生匹配,根据图,可以看到1号可以与8号匹配,那么就改变匹配对象。1号与8号匹配,3号与六号匹配。
要注意的是,每个男生对于可以与之匹配的女生,只考虑一次
循环往复,可以找到最大匹配数。
题目
给定一个二分图,其中左半部包含 n1 个点(编号 1∼n1 ),右半部包含 n2 个点(编号 1∼n2 ),二分图共包含 m 条边。数据保证任意一条边的两个端点都不可能在同一部分中。
请你求出二分图的最大匹配数。
给定一个二分图 G,在 G 的一个子图 M 中,M 的边集 [E] 中的任意两条边都不依附于同一个顶点,则称 M 是一个匹配。所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配,其边数即为最大匹配数。
输入格式
第一行包含三个整数 n1、n2、m(分别表示左部顶点数、右部顶点数、边数 )。
接下来 m 行,每行包含两个整数 u 和 v,表示左半顶点集中的点 u 和右半顶点集中的点 v 之间存在一条边。
输出格式
输出一个整数,表示二分图的最大匹配数。
数据范围
1≤n1,n2≤500
1≤u≤n1
1≤v≤n2
1≤m≤1e5
输入样例
cpp
2 2 4
1 1
1 2
2 1
2 2 输出样例
cpp
2 代码实现
cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int P = 1e9+7;
const int N = 2e5+10;
const int INF = 0x3f3f3f3f;
int n1,n2,m;
int h[N],e[N],ne[N],idx;
int match[N];
bool st[N];
void add(int a,int b)
{
e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}
bool find(int x)
{
for(int i = h[x];i!=-1;i = ne[i])
{
int j = e[i];
if(!st[j])//如果这个女生还没有考虑过
{
st[j] = true;
//如果这个女生还没有匹配或者已经匹配了但是可以找到另一个女生与已经和当前这个女生匹配的男生进行匹配
//与上文说的三号男生相同
if(match[j]==0||find(match[j]))
{
match[j] = x;
return true ;
}
}
}
return false;
}
int main()
{
cin>>n1>>n2>>m;
memset(h,-1,sizeof h);
while(m--)
{
int a,b;
cin>>a>>b;
add(a,b);
}
int res = 0;//存的是匹配的数量
for(int i = 1;i<=n1;i++)
{
memset(st,false,sizeof st);//每次与之匹配的点只考虑一次
if(find(i)) res++;//如果可以找到匹配的点,答案加1
}
cout<<res<<endl;
return 0;
}