本篇将讲解计数原理和最基础的排列数和组合数
一:计数原理
分类加法原理:
情景:现在你有3趟明天的火车,还有2班明天的飞机,问你有多少种方式能到达目的地
显然我们既可以坐火车,也可以坐飞机,而且坐了火车就不能坐飞机,坐了飞机就不能坐火车,它们的选择是彼此独立的
所以我们有3+2=5种方案能到达目的地
这就是分类加法原理,就是我们的路径是分类的,每个选择彼此独立
分步乘法原理:
情景:现在你有3件衣服和2件裤子,你有多少种穿搭方案出门?
二:排列数
情景:现在有n个人排队,问有多少种排队方案
首先假设n-1个人有x种排列方案,那么对于第n个人来说,他可以排在每个人的前面,也可以排在每个人的后面,如图,我们发现对于第n个人,无论前n-1个人排列如何,我们都可以把第n个人放在红色的位置,并且无论放在哪里都会变成一个新的排列,根据乘法原理,它的总方案数,就是前n-1个人的方案总数乘以第n个人的方案数,而第n个人的方案数是n,所以我们知道,3个人排列就是前2个人排列数*3,4个人就是前3个人排列数*4,而第一个人排列数一定是1,所以我们得到了全排列的定义(即n个人选n个人排队有多少种方案)
n的全排列数即为n的阶乘,符号是
、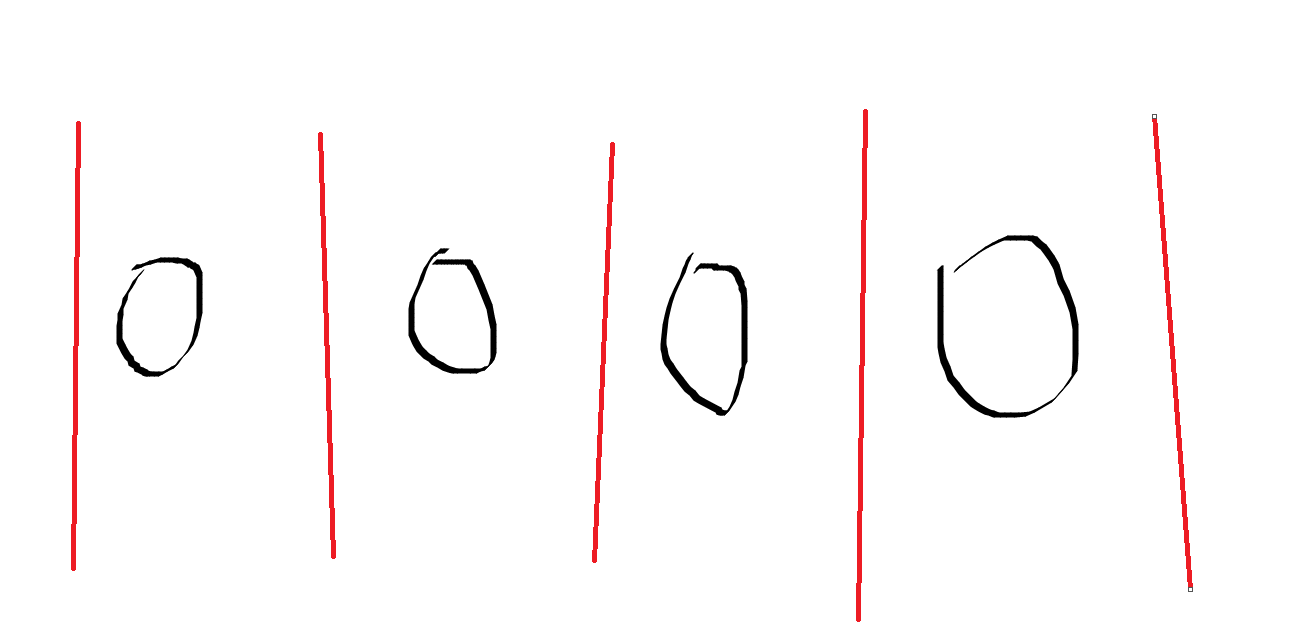
或者有另一种理解方式:
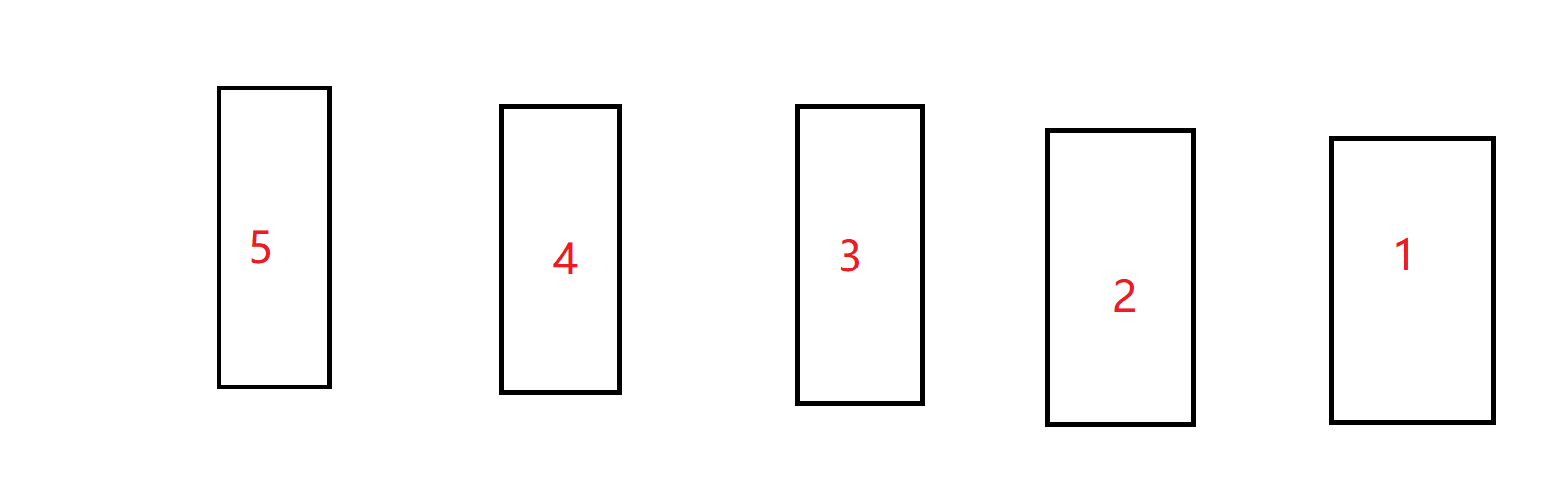
既然5个人排队,那我们就是一共有5个位置可以放人,我们考虑每个位置有多少种方案,根据乘法原理,最终的排列数就是每个位置的方案数之积
比如第一个位置,现在5个人都没有排,所以每个人都可以站在第一个位置,所以第一个位置方案数是5
第二个位置呢?既然有一个人去站第一个位置了,那么剩下的4个人都可以站在第二个位置,所以第二个位置方案数是4
第三个位置呢?既然有2个人去1,2位置了,那么剩下3个随便站,方案数是3
同理,4位置方案数是4
最后只剩1个人了,只能站在第五个位置,所以第五个位置方案数是1
最终答案是5*4*3*2*1,也是n的阶乘
然后我们考虑n个人里选m个排列,我们发现在第二个图中,假如5个选3个,那么后面两个位置就没有了,我们只需要考虑前3个位置的方案数,然后前3个位置的方案数分别是5,4,3,和刚才全排列没有区别,所以答案是5*4*3
所以我们得出了排列数的公式
其实很好理解,全排列数是n!,相当于被扣去(m-1)个位置,所以那一部分的方案数就不算了,除一下就好了
三:组合数
我们回顾一下排列数,在排列中,我们认为13和31是不同的,算两种排列,但是在组合中,我们认为它们是相同的,所以数量肯定要减少,至于减少多少:
我们考虑一个排列A,比如A=123,那么其实123,,132,213,231,312,321都算一种组合数,但它们算6种排列
所以我们可以发现,对于A的全排列,它们实际上都是一个组合
所以我们发现,组合相比排列,"缩水"的地方实际在于,排列A的全排列(比如A=123,它的全排列就是从1-3所有排列的方案),它们算了很多次排列,但只算了一个组合
所以我们自然而然的想到,要算一个组合数,先算出它的排列数,然后用排列数除以每个数多贡献出的数量,也就是除以n的全排列(因为1-n的全排列只算一个组合)
举个例子,比如我让4个人挑2个去排列,那么所有的排列方式应该是这样的
1 2
2 1
1 3
3 1
2 3
3 2
1 4
4 1
2 4
4 2
3 4
4 3
共12种排列方式
然而我们发现,每相邻两种排列方式,它们只改变了顺序,而没有改变元素种类,组合的本质是不计顺序的排列(1 2和2 1的区别仅仅是顺序)
那我们发现对于任意一个排列A,A与其全排列的区别就仅仅是顺序
比如A=123,它的全排列是
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
然而它们内部的数没有区别,所以尽管算6种排列,但是只能算一种组合
比如567和765是两种排列,但只是一种组合
所以我们发现,对于一个组合数S,它其实等于对应的排列数除以每个组合对应的全排列数,因为每个组合内部的数量是相同的,所以除它们共同的全排列数即可
比如还是4个人里选2个组合,那么符合条件的组合分别有:
1 2(包括2 1)
1 3(包括3 1)
1 4(包括4 1)
2 3(包括3 2)
2 4(包括4 2)
3 4(包括4 3)
由于是选2个进行组合,所以只需要用4个人选2个的排列数,去除以2的全排列数,就是2的阶乘即可
形式化地,我们对n个人选m个人组合的方案数计算如下: