【题目描述】
农夫John发现做出全威斯康辛州最甜的黄油的方法:糖。把糖放在一片牧场上,他知道N(1≤N≤500)只奶牛会过来舔它,这样就能做出能卖好价钱的超甜黄油。当然,他将付出额外的费用在奶牛上。
农夫John很狡猾。像以前的巴甫洛夫,他知道他可以训练这些奶牛,让它们在听到铃声时去一个特定的牧场。他打算将糖放在那里然后下午发出铃声,以至他可以在晚上挤奶。
农夫John知道每只奶牛都在各自喜欢的牧场(一个牧场不一定只有一头牛)。给出各头牛在的牧场和牧场间的路线,找出使所有牛到达的路程和最短的牧场(他将把糖放在那)。
【输入】
第一行: 三个数:奶牛数N,牧场数P(2≤P≤800),牧场间道路数C(1≤C≤1450)。
第二行到第N+1行: 1到N头奶牛所在的牧场号。
第N+2行到第N+C+1行:每行有三个数:相连的牧场A、B,两牧场间距(1≤D≤255),当然,连接是双向的。
【输出】
一行 输出奶牛必须行走的最小的距离和。
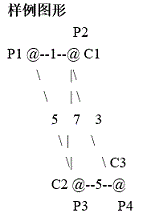
【输入样例】
3 4 5
2
3
4
1 2 1
1 3 5
2 3 7
2 4 3
3 4 5【输出样例】
8【提示】
说明:放在4号牧场最优。
0. 前言
在图论题目中,算法的选择往往比代码实现更重要。很多同学拿到题,看到是"求最短路",反手就是一个 Floyd 或者 Bellman-Ford,结果评测机直接给出 tle(这道题信息学奥赛一本通测试点很水)。
今天我们以这道题为例,深度复盘三种最短路算法在P=800这个微妙数据范围下的表现,并总结学生在实战中易犯的错误。
1. 题目概要与数据分析
题目:给定P个牧场和C条双向道路,以及N头奶牛的位置。求把糖放在哪个牧场,能使所有奶牛到达该牧场的距离之和最小。
数据范围:
-
牧场数 P<=800
-
道路数 C<=1450
-
奶牛数 N<=500
教练分析:
这是一道多源最短路的变种问题。我们需要枚举每一个牧场作为终点,计算它到所有奶牛的最短路径和。
看似P=800不大,但如果算法的时间复杂度是O(P^3),计算量将达到5.12*10^8。在 CCF 的标准评测环境(通常 1秒约等于10^8次运算)下,这属于高危操作。
2. 方案一:Floyd-Warshall(容易TLE)
这是初学者最喜欢的算法,因为代码短,逻辑简单。但在本题中,这是典型的"骗分"写法。即使某些弱数据能过,也不代表这是正确的算法选型。这道题应该测试数据很水,可以直接过
复杂度分析:O(P^3)约等于5.12*10^8。在 1 秒的时限下,这处于超时的边缘。
完整代码
cpp
//floyd
#include <iostream>
#include <cstring>
using namespace std;
int n,p,c;
int s[510];//存储每头奶牛在哪一个牧场
int g[810][810];
void floyd(){
for(int k=1;k<=p;k++){
for(int i=1;i<=p;i++){
for(int j=1;j<=p;j++){
if(g[i][j]>g[i][k]+g[k][j])
g[i][j]=g[i][k]+g[k][j];
}
}
}
}
int main(){
cin>>n>>p>>c;//奶牛数 牧场数 牧场间道路数
for(int i=1;i<=n;i++) cin>>s[i];//存储每头奶牛在哪一个牧场
memset(g,0x3f,sizeof(g));//初始化g数组边与边之间距离为无穷(不可达)
for(int i=1;i<=p;i++) g[i][i]=0;//初始化每个牧场和自己的距离为0
//存边建图 邻接矩阵
for(int i=1;i<=c;i++){
int u,v,w;
cin>>u>>v>>w;
g[u][v]=w;//牧场是双向的
g[v][u]=w;
}
floyd();
int mi=0x3f3f3f3f;//初始化最短路程和为极大
for(int i=1;i<=p;i++){//遍历p个牧场分别作为放糖牧场,找出路程和最短牧场
int dis=0;
for(int j=1;j<=n;j++){//遍历n头奶牛的位置
dis+=g[i][s[j]];//起点是i 终点是s[j]
}
mi=min(mi,dis);
}
cout<<mi;
return 0;
}3. 方案二:Bellman-Ford(甚至不如 Floyd)
很多同学认为 Bellman-Ford 是单源最短路,应该比 Floyd 快。但在求"所有点到所有点"时,我们需要跑P次 Bellman-Ford。
复杂度分析:P*O(P*C)约等于800*800*1450约等于9.2*10^8。
结论:用了flag标记一轮不更新就退出后,这道题可能测试数据太水了,也能过
完整代码
cpp
//Bellman-ford算法
#include <iostream>
#include <cstring>
using namespace std;
int n,p,c;
int dis[810];//记录牧场到源点的距离
int s[510];//记录每头奶牛在哪个牧场
struct edge{
int u;
int v;
int w;
}e[3000];
void ford(int k){
dis[k]=0;//源点到自己的距离为0
for(int i=1;i<p;i++){//迭代p-1轮(p个牧场)
bool flag=false;//记录本轮是否有距离发生更新
for(int j=1;j<=2*c;j++){//因为是双向边,所以要2*c
int x=e[j].u;
int y=e[j].v;
int z=e[j].w;
if(dis[y]>dis[x]+z && dis[x]!=0x3f3f3f3f){
dis[y]=dis[x]+z;
flag=true;
}
}
//本来没有发生更新,后面就也不会更新了
if(flag==false) break;
}
}
int main(){
cin>>n>>p>>c;
for(int i=1;i<=n;i++) cin>>s[i];//记录每头奶牛在哪个牧场
for(int i=1;i<=c;i++){
int a,b,d;
cin>>a>>b>>d;
e[i].u=a;
e[i].v=b;
e[i].w=d;
e[i+c].u=b;//连接是双向的,所以要存储双向边
e[i+c].v=a;
e[i+c].w=d;
}
int mi=0x3f3f3f3f;//初始化最短距离
//遍历p个牧场,分别作为源点,计算其他牧场到源点距离
for(int i=1;i<=p;i++){
int d=0;//本轮最短距离
//初始化dis数组为极大
for(int j=1;j<=809;j++) dis[j]=0x3f3f3f3f;
ford(i);
for(int j=1;j<=n;j++){
int o=s[j];//找出每头牛在哪个牧场
d+=dis[o];
}
mi=min(mi,d);
}
cout<<mi;
return 0;
}4. 方案三:Dijkstra 堆优化(标准正解)
面对正权图且P较大、图稀疏(C远小于P^2)的情况,Dijkstra 堆优化是唯一指定正解。
复杂度分析:P*O(C log P)约等于800 *1450*10 约等于1.1 *10^7。
结论:千万级别的运算量,几十毫秒即可通过。
完整代码
cpp
//dijkstra邻接表+堆优化
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
int n,p,c;
int s[510];//存每头奶牛在几号牧场
int h[810];//记录每个牧场的头指针
int vtex[3000];//最多有1450条道路,道路是双向的,所以开3000足够
int nxt[3000];
int wt[3000];//记录牧场与每个临接牧场之间道路的距离
int idx;
int dis[810];//记录每个牧场到源点的距离
int vis[810];//记录每个牧场是否已经出队使用过(点亮过)
struct node{
int id;//牧场编号
int w;//牧场到源点的距离
//重载运算符,修改为小根堆
friend bool operator <(node a,node b){
return a.w>b.w;
}
};
priority_queue<node> q;
void dijkstra(int k){
dis[k]=0;//源牧场到源点(自身)的距离为0
node tmp;
tmp.id=k;
tmp.w=0;
q.push(tmp);//源点入队
while(!q.empty()){
tmp=q.top();//访问队首元素
q.pop();//队首出队
//懒惰删除,如果tmp已经出队过(点亮过)就直接跳过
//因为可能有多个进入队列,但小根堆保证dis最小的优先出队了,后面的就是垃圾数据
if(vis[tmp.id]==1) continue;
vis[tmp.id]=1;//没有出队过就现在打上标记
int nid=tmp.id;//当前出队节点编号
int p=h[nid];//当前出队节点tmp的头指针
while(p!=-1){
if(vis[vtex[p]]==0){//如果tmp的临接点没有出队过(没有点亮过)
//如果临接点到源点的距离大于(tmp到源点的距离+tmp与邻接点的边权)就更新
if(dis[vtex[p]]>dis[nid]+wt[p]){
dis[vtex[p]]=dis[nid]+wt[p];
//如果发生了距离更新才有入队意义
q.push({vtex[p],dis[vtex[p]]});
}
}
p=nxt[p];//指针指向下一个邻接点
}
}
}
void addedge(int u,int v,int w){
vtex[idx]=v;
nxt[idx]=h[u];
wt[idx]=w;
h[u]=idx++;
}
int main(){
cin>>n>>p>>c;//奶牛数N 牧场数P 牧场间道路数C
for(int i=1;i<=n;i++) cin>>s[i];//每头奶牛在几号牧场
//初始化头指针数组为-1不能丢,不然dijkstra就会死循环
memset(h,-1,sizeof(h));
//建图
for(int i=1;i<=c;i++){
int u,v,w;
cin>>u>>v>>w;
addedge(u,v,w);//牧场间连接是双向的,所以要把双向边都加进去
addedge(v,u,w);
}
int mi=0x3f3f3f3f;//先初始化最短距离为无穷
for(int i=1;i<=p;i++){//遍历所有牧场,轮流作为源点,去求其他牧场到源点到最短路径
int d=0;//每轮的最短距离
memset(dis,0x3f,sizeof(dis));//每轮都要初始化dis数组为无穷
memset(vis,0,sizeof(vis));//每轮Dijkstra之前都要把vis数组初始化
dijkstra(i);
for(int j=1;j<=n;j++){//遍历所有奶牛位置
int o=s[j];//奶牛所在牧场
d+=dis[o];
}
mi=min(mi,d);
}
cout<<mi;
return 0;
}5. 复盘:学生常见易错点总结
在看学生作业时,这三个代码暴露出的问题非常具有代表性,请大家对照自查:
- 数据类型的隐式混用
在 Bellman-Ford 代码中,出现了 dis[x] != 1e9。
-
问题 :
dis是int数组,而1e9是double字面量。虽然编译器会进行隐式转换,但这是一种比较差的编程习惯。 -
后果 :在更复杂的计算中,
double的精度漂移可能导致!=判断失效。 -
规范 :整型数组请使用
0x3f3f3f3f,浮点型数组请使用1e18,严禁混用。
- 复杂度估算的缺失
很多同学看到题目 AC 了就沾沾自喜。
-
真相:Floyd 和 Bellman-Ford 能过这道题,只能说明测试数据过水,没有跑满P=800的上限。
-
警示 :在 CSP/NOIP 赛场上,数据是极强的。不要用 AC 来验证算法的正确性,要用复杂度分析来验证。
3. 多次 Dijkstra 的初始化陷阱
-
问题:本题需要枚举每个牧场跑 Dijkstra。
-
易错 :很多同学在循环内忘记
memset(dis)和memset(vis),导致沿用了上一轮的脏数据。 -
规范 :在调用
dijkstra(i)之前,必须彻底清空相关状态数组。
4. 数组边界的卡死
-
问题 :题目C<=1450,双向边需要2900。有同学开
vtex[2910]。 -
建议 :空间允许的情况下,建议开到
MAXC=6000或至少3000。不要在边界上走钢丝,防止 re。
总结:
-
P <=100用Floyd
-
P<=1000(且单源) 用Bellman-Ford/SPFA
-
P<=10000+用Dijkstra邻接表+堆优化
-
本题P=800且需跑P遍必须 Dijkstra。
后续有时间再更新spfa做法