1、题干
给定一个m x n的矩阵,如果一个元素为0 ,则将其所在行和列的所有元素都设为0 。请使用原地算法。
示例 1:
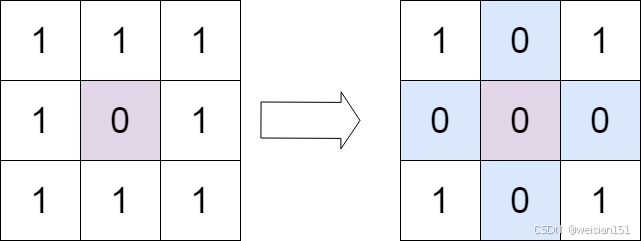
输入:matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出:[[1,0,1],[0,0,0],[1,0,1]]
示例 2:
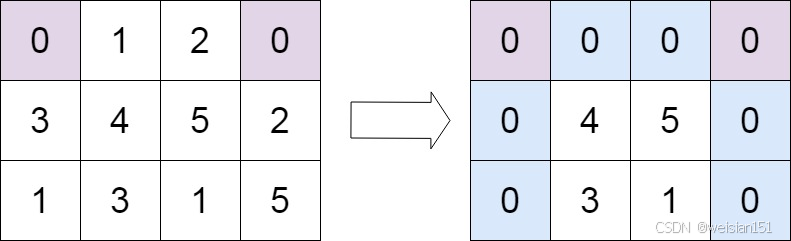
输入:matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出:[[0,0,0,0],[0,4,5,0],[0,3,1,0]]
提示:
m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-231 <= matrix[i][j] <= 231 - 1
2、解题
本题要求,遍历元素,发现为0的元素时,将其列和行均变为0;
注意不能在遍历的过程中同步进行0值的修改。想一下,如果在遍历时就将后面行的元素修改成了0,那么之后行的遍历时,就会将改行全部变为0,进而导致整个列也全部都变成0,最终形成全0的局面。
方法一:(辅助数组标记法)
在第一次遍历数据时,使用辅助数组记住0元素的下标位置。在第二次遍历时,将根据辅助数组的标记进行修改。
代码示例:
java
import java.util.Arrays;
public class Test48 {
public static void setZeroes(int[][] matrix) {
int rowLen = matrix.length;
int colLen = matrix[0].length;
boolean[] hasRow = new boolean[rowLen]; // 辅助数组,记录为0的行
boolean[] hasCol = new boolean[colLen]; // 辅助数组,记录为0的列
for (int i = 0; i < rowLen; i++) {
for (int j = 0; j < colLen; j++) {
if (matrix[i][j]==0){ // 第一次遍历,填充辅助数组
hasRow[i] = true;
hasCol[j] = true;
}
}
}
for (int i = 0; i < rowLen; i++) {
for (int j = 0; j < colLen; j++) {
if (hasRow[i] || hasCol[j]){ // 第二次遍历,根据辅助数组进行数据的修改
matrix[i][j]=0;
}
}
}
}
public static void main(String[] args) {
int[][] matrix = {{1, 1, 1}, {1, 0, 1}, {1, 1, 1}};
setZeroes(matrix);
System.out.println(Arrays.deepToString(matrix));
}
}方法二:(使用两个标记变量)
使用两个变量标记。实际上是方法一节省空间的一种表现。
将第0行和第0列作为辅助空间,先标记在修改元素。但第0行和第0列的元素不能根据被修改后的值进行修改,所以还要添加两个变量先记录第0行和第0列是否包含0的存在。
逻辑顺序:
(1)、先判断第0行和第0列是否包含0,生成对应的标记。
(2)、遍历之后非0行和非0列的元素,使用第0行和第0列作为辅助空间,进行标记。
(3)、再次遍历非0行和非0列的元素,使用第0行和第0列辅助数组空间进行值的修改。
(4)、使用第0行和第0列的标记,对第0行和第0列的元素进行修改。
代码示例:
java
import java.util.Arrays;
public class Test48 {
public static void setZeroes(int[][] matrix) {
int rowLen = matrix.length;
int colLen = matrix[0].length;
boolean isFirstRow = false; // 第0行是否包含0。这里使用第0行作为行辅助空间,进行后续元素的修改参照,最后在根据第0行单独的标记进行该行的修改。
boolean isFirstCol = false; // 第0列是否包含0。这里使用第0列作为列辅助空间,进行后续元素的修改参照,最后在根据第0列单独的标记进行该列的修改。
for (int i = 0; i < colLen; i++) {
if (matrix[0][i]==0){ // 第0行是否包含0遍历处理
isFirstRow = true;
break;
}
}
for (int i = 0; i < rowLen; i++) {
if (matrix[i][0]==0){ // 第0列是否包含0遍历处理
isFirstCol = true;
break;
}
}
// 遍历之后的元素,使用第0行和第0列作为辅助数组标记
for (int i = 1; i < rowLen; i++) {
for (int j = 1; j < colLen; j++) {
// 先标记
if(matrix[i][j]==0){
matrix[0][j] = 0;
matrix[i][0] = 0;
}
}
}
for (int i = 1; i < rowLen; i++) {
for (int j = 1; j < colLen; j++) {
// 根据标记在进行元素修改
if(matrix[i][0]==0 || matrix[0][j]==0){
matrix[i][j] = 0;
}
}
}
// 根据第0行和第0列的标记,进行第0行和第0列的修改
if (isFirstRow){
for (int i = 0; i < colLen; i++) {
matrix[0][i] = 0;
}
}
if (isFirstCol){
for (int i = 0; i < rowLen; i++) {
matrix[i][0] = 0;
}
}
}
public static void main(String[] args) {
int[][] matrix = {{1, 1, 1}, {1, 0, 1}, {1, 1, 1}};
setZeroes(matrix);
System.out.println(Arrays.deepToString(matrix));
}
}向阳前行,Dare To Be!!!