56.一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
输入: strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出: 4
**解释:**最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
示例 2:
输入: strs = ["10", "0", "1"], m = 1, n = 1
输出: 2
解释: 最大的子集是 {"0", "1"} ,所以答案是 2 。
提示:
1 <= strs.length <= 6001 <= strs[i].length <= 100strs[i]仅由'0'和'1'组成1 <= m, n <= 100
如果是01背包的话
那么dp[i] [j]表示的就是:从前i个物品中挑选,总体积不超过j,所有选法中,最大的价值
二维费用
又多了一个限制条件
dp[i] [j] [k] :从前i个字符串中挑选,0的个数不超过j,字符1的个数不超过k,所有的选法中,最大的长度
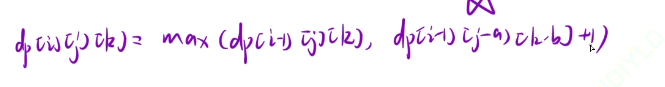
C++
class Solution
{
public:
int findMaxForm(vector<string>& strs, int m, int n)
{
int len=strs.size();
vector<vector<vector<int>>>dp(len+1,vector<vector<int>>(m+1,vector<int>(n+1)));
//我们这里是不需要进行初始化操作的
for(int i=1;i<=len;i++)//遍历字符串的
{
//统计0和1的个数
int a=0,b=0;//a:当前考虑的第 `i` 个字符串中 0 的数量,b:当前考虑的第 `i` 个字符串中 1 的数量
for(auto ch:strs[i-1])//我们这里是需要进行-1进行数组映射的,因为我们多加了一列的
{
//遍历strs中的每一个字符串里面的字符
if(ch=='0')a++;
else b++;
}
for(int j=0;j<=m;j++)
{
for(int k=0;k<=n;k++)
{
dp[i][j][k]=dp[i-1][j][k];//这个是我们i位置不选的情况
if(j>=a&&k>=b)
//这个条件判断的作用是检查当前可用的 0 和 1 的数量是否足够选择第 `i` 个字符串。只有当当前可用的 0 的数量 `j` 大于等于第 `i` 个字符串中 0 的数量 `a`,并且当前可用的 1 的数量 `k` 大于等于第 `i` 个字符串中 1 的数量 `b` 时,才可以选择第 `i` 个字符串。
dp[i][j][k]=max(dp[i][j][k],dp[i-1][j-a][k-b]+1);
}
}
}
return dp[len][m][n];
}
};dp[i - 1][j - a][k - b] 表示在前 i - 1 个字符串中选择,在 0 的数量不超过 j - a 且 1 的数量不超过 k - b 的情况下所能得到的最大子集的字符串个数,因为选择了第 i 个字符串,所以要在这个基础上加 1。
max(dp[i][j][k], dp[i - 1][j - a][k - b] + 1):取不选择第 i 个字符串和选择第 i 个字符串这两种情况中的最大值,更新 dp[i][j][k] 的值。
下面的代码是空间优化
这里是模仿01背包的模版,可以按照01背包的样例进行空间优化 的
C++
class Solution
{
public:
int findMaxForm(vector<string>& strs, int m, int n)
{
int len=strs.size();
vector<vector<int>>dp(m+1,vector<int>(n+1));
//我们这里是不需要进行初始化操作的
for(int i=1;i<=len;i++)//遍历字符串的
{
//统计0和1的个数
int a=0,b=0;//a表示0的个数,b表示1个数
for(auto ch:strs[i-1])//我们这里是需要进行-1进行数组映射的,因为我们多加了一列的
{
//遍历strs中的每一个字符串里面的字符
if(ch=='0')a++;
else b++;
}
for(int j=m;j>=a;j--)
{
for(int k=n;k>=b;k--)
{
dp[j][k]=max(dp[j][k],dp[j-a][k-b]+1);
}
}
}
return dp[m][n];
}
};57.盈利计划
集团里有 n 名员工,他们可以完成各种各样的工作创造利润。
第 i 种工作会产生 profit[i] 的利润,它要求 group[i] 名成员共同参与。如果成员参与了其中一项工作,就不能参与另一项工作。
工作的任何至少产生 minProfit 利润的子集称为 盈利计划 。并且工作的成员总数最多为 n 。
有多少种计划可以选择?因为答案很大,所以 返回结果模 10^9 + 7 的值。
示例 1:
输入: n = 5, minProfit = 3, group = [2,2], profit = [2,3]
输出: 2
解释: 至少产生 3 的利润,该集团可以完成工作 0 和工作 1 ,或仅完成工作 1 。
总的来说,有两种计划。
示例 2:
输入: n = 10, minProfit = 5, group = [2,3,5], profit = [6,7,8]
输出: 7
解释: 至少产生 5 的利润,只要完成其中一种工作就行,所以该集团可以完成任何工作。
有 7 种可能的计划:(0),(1),(2),(0,1),(0,2),(1,2),以及 (0,1,2) 。
提示:
1 <= n <= 1000 <= minProfit <= 1001 <= group.length <= 1001 <= group[i] <= 100profit.length == group.length0 <= profit[i] <= 100
第0种工作会产生2种利润,需要两名员工
第1种工作会产生3种利润,需要两名员工
说白了就是从g和p数组中挑选,挑选的值要满足右边的条件,就是参与工作的人数要小于n
利润要大于minprofit

这里的话条件需要满足两个,并且是一个01背包问题,
所以是二位费用的背包问题
这里的工作只能是选和不选两种情况,所以的话是01背包而不是完全背包
dp[i] [j] [k]:表示:从前i个计划中挑选,总人数不超过j,总利润至少为k,一共有多少种选法
如果我们i位置的利润大于等于k了,那么我们就在i-1区域里面满足利润大于等于0就行了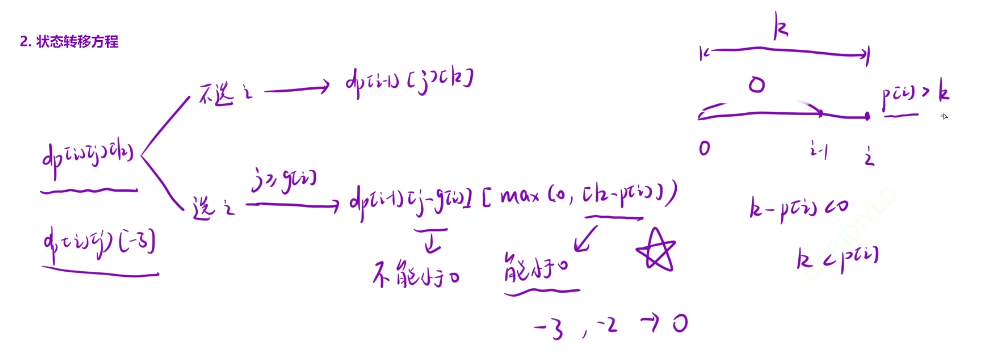
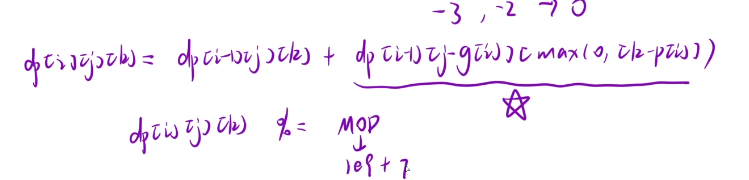
初始化:当我们没有任务的时候并且没有利润,无论人数有多少,我只有一种选择,就是一个空集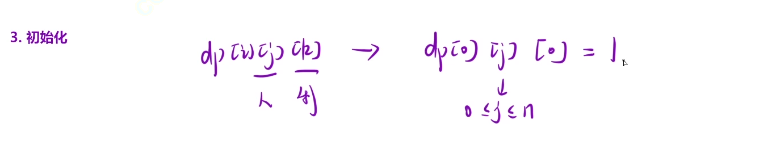
返回值
dp[len] [n] [m]
C++
class Solution
{
public:
int profitableSchemes(int n, int m, vector<int>& g, vector<int>& p)
{
const int MOD=1e9+7;//取模的数
int len=g.size();
vector<vector<vector<int>>>dp(len+1,vector<vector<int>>(n+1,vector<int>(m+1)));
for(int j=0;j<=n;j++)dp[0][j][0]=1;//没有工作,没有利润的情况下,无论人数有多少都是空集的,只存在空集这一种情况的
for(int i=1;i<=len;i++)
{
for(int j=0;j<=n;j++)
{
for(int k=0;k<=m;k++)
{
dp[i][j][k]=dp[i-1][j][k];//就是i位置不选的情况,去i-1位置选择
if(j>=g[i-1])//必须满足人数大于g[i],员工人数至少为n
dp[i][j][k]+=dp[i-1][j-g[i-1]][max(0,k-p[i-1])];
dp[i][j][k]%=MOD;//防止超出int的值
}
}
}
return dp[len][n][m];
}
};
下面是空间优化的代码
C++
class Solution
{
public:
int profitableSchemes(int n, int m, vector<int>& g, vector<int>& p)
{
const int MOD=1e9+7;//取模的数
int len=g.size();
vector<vector<int>>dp(n+1,vector<int>(m+1));
for(int j=0;j<=n;j++)dp[j][0]=1;//没有工作,没有利润的情况下,无论人数有多少都是空集的,只存在空集这一种情况的
for(int i=1;i<=len;i++)
{
for(int j=n;j>=g[i-1];j--)
{
for(int k=m;k>=0;k--)
{
dp[j][k]+=dp[j-g[i-1]][max(0,k-p[i-1])];
dp[j][k]%=MOD;//防止超出int的值
}
}
}
return dp[n][m];
}
};