力扣题目142. 环形链表 II的解法分享，附图解

题目：

Problem: 142. 环形链表 II

图解：

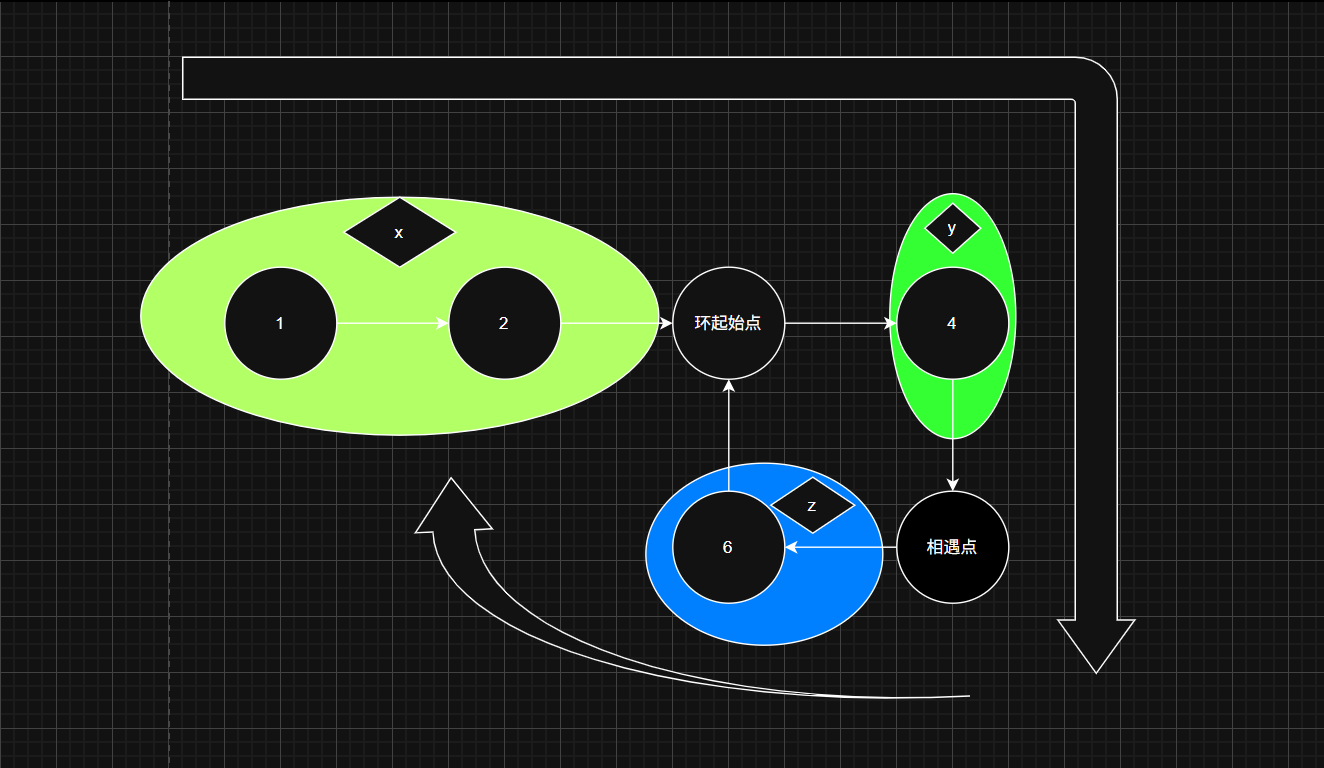
思路：

设两个指针fast和slow，fast每次走2步，slow每次走1步

设n为fast比slow多走的圈数

当相遇的时候根据fast和slow的步数关系：

2（x+y）=x+y+（y+z）*n

简单化简：

x=（n-1）（y+z）+z

此时我们可以得知x与z的关系，因为y+z为一个圈，所以x等于z再加上一个圈的倍数
此时定义一个指向头节点的指针，然后slow继续向前走，此时一定会在环的起始点相遇，因为此时恰好满足x等于z再加上一个圈的倍数的数量关系。

反思：

其实很多时候，我们可以直接带入特殊值来直接看待数量关系直接令n=1便会很快发现这题的规律，取一些特殊值来达到快速定位规律的方法在很多题都适用，即从一般到特殊的分析方式。

复制代码

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
          if (head == null || head.next == null|| head.next.next == null) {
            return null; // 无环
        }
        ListNode fastNode=head.next.next;
        ListNode slowNode=head.next;
        while (fastNode != null && fastNode.next != null && fastNode != slowNode) {
            fastNode = fastNode.next.next;
            slowNode = slowNode.next;
        }
        if (fastNode == null || fastNode.next == null) {
        return null; // 无环
    }
//定义一个指针index1，在头结点处定一个指针index2
        ListNode index1=head;
        ListNode index2=fastNode;
        while(index1!=index2 && index2 != null && index1!= null){
            index1=index1.next;
            index2=index2.next;
        }
        return index1;
    }
}