前言

排序
QuickSort(非递归)
需要用到栈的知识(栈的复习)
需要用到快排的知识(快排复习)
前置代码
cpp
void Swap(int& x, int& y)
{
int tmp = x;
x = y;
y = tmp;
}
int GetMidNumber(vector<int>&arr,int left, int right)
{
int mid = (left + right) / 2;
if ((arr[mid] > arr[left] && arr[mid] < arr[right]) ||
(arr[mid] > arr[right] && arr[mid] < arr[left])) return mid;
if ((arr[right] > arr[left] && arr[right] < arr[mid]) ||
(arr[right] > arr[mid] && arr[right] < arr[left])) return right;
return left;
}
//经典法
int Partition1(vector<int>& arr, int left, int right)
{
int mid = GetMidNumber(arr, left, right);
Swap(arr[left], arr[mid]);
int pivot = left;
int cur = left + 1;
int prev = left;
while (cur <= right)
{
if (arr[cur] < arr[pivot] && ++prev!=cur)
{
Swap(arr[cur], arr[prev]);
}
cur++;
}
Swap(arr[pivot], arr[prev]);
return prev;
}
//前后指针
int Partition2(vector<int>& arr, int left, int right)
{
int mid = GetMidNumber(arr, left, right);
Swap(arr[left], arr[mid]);
int pivot = left;
int low = left;
int high = right;
while (low < high)
{
while (low<high && arr[high] >= arr[pivot]) high--;
while (low<high && arr[low] <= arr[pivot]) low++;
Swap(arr[low], arr[high]);
}
Swap(arr[low], arr[pivot]);
return low;
}
cpp
void QuickSortNonR1(vector<int>& arr)
{
stack<int>s;
int n = arr.size();
s.push(0);
s.push(n - 1);
while (!s.empty())
{
int high = s.top();
s.pop();
int low = s.top();
s.pop();
int pivotindex = Partition2(arr, low, high);
if (pivotindex + 1 < high)
{
s.push(pivotindex + 1);
s.push(high);
}
if(pivotindex - 1 > low)
{
s.push(low);
s.push(pivotindex - 1);
}
}
}分析
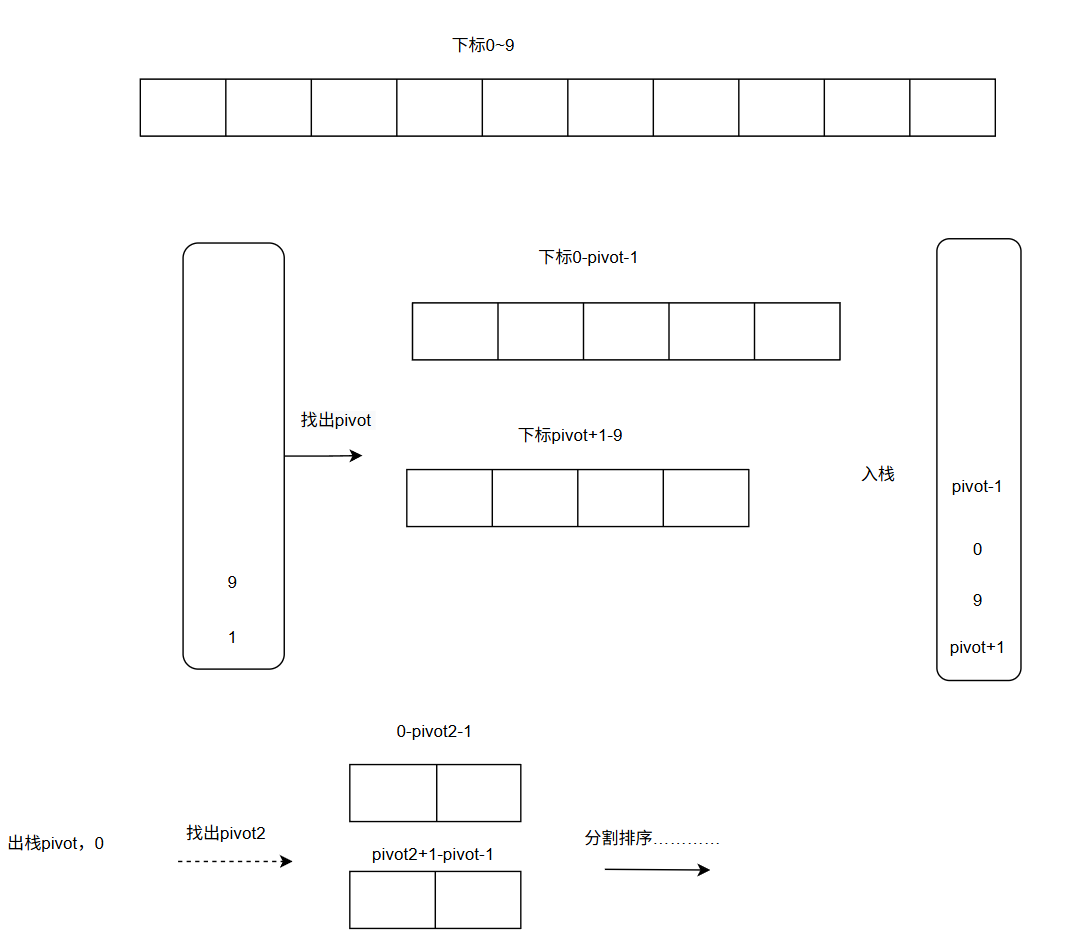
用栈代替递归:不再通过函数自身调用,而是用一个栈来存储需要排序的子数组的范围(起始和结束索引)。
迭代处理:只要栈不为空,就不断弹出子数组范围,进行**分区(partition)**操作。
压入子任务:分区后,将新产生的两个子数组的范围压回栈中,等待后续处理。
解析
1.栈的特点是先进后出,所以先进low后进high,故先出high,后出low。
2.栈把数组分割同递归相似,pivotIndex + 1 / -1需要判断与low,high 的大小,确定边界条件。
3.此版本先将右侧入栈,后将左侧入栈,类似于前序遍历,把左侧排完再派右侧。可以自由调整先排哪一侧。
cpp
//先左后右排序
if (pivotindex + 1 < high)
{
s.push(pivotindex + 1);
s.push(high);
}
if(pivotindex - 1 > low)
{
s.push(low);
s.push(pivotindex - 1);
}优势
避免栈溢出:在最坏情况下(例如,输入数组已经有序),递归版本的快速排序会产生很深的调用栈,可能导致程序崩溃。非递归版本使用自定义的栈来管理任务,从而绕过了系统栈的深度限制。
归并排序(递归)
cpp
void Merge_Sort(vector<int>&arr,int left,int right,vector<int>&tmp)
{
if (left >= right) return;
int mid = (left + right) / 2;
Merge_Sort(arr, left, mid, tmp);
Merge_Sort(arr, mid+1, right, tmp);
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int i = left;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[i++] = arr[begin1++];
}
else
{
tmp[i++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
copy(tmp.begin()+left, tmp.begin() + right + 1, arr.begin()+left);
}分析
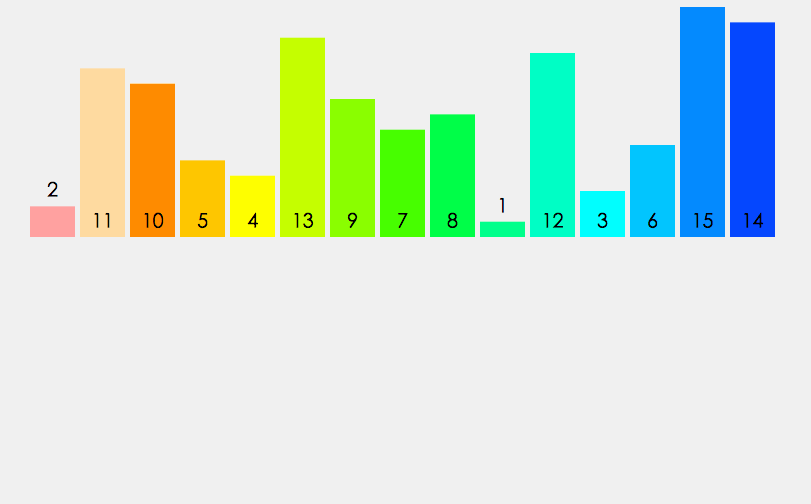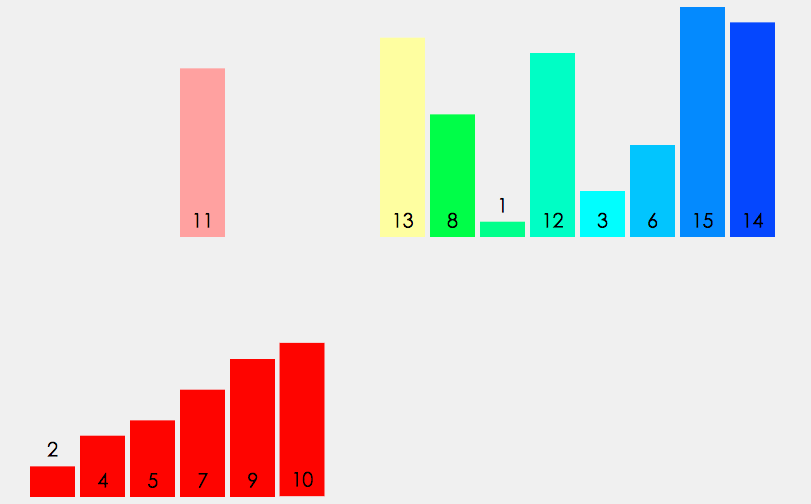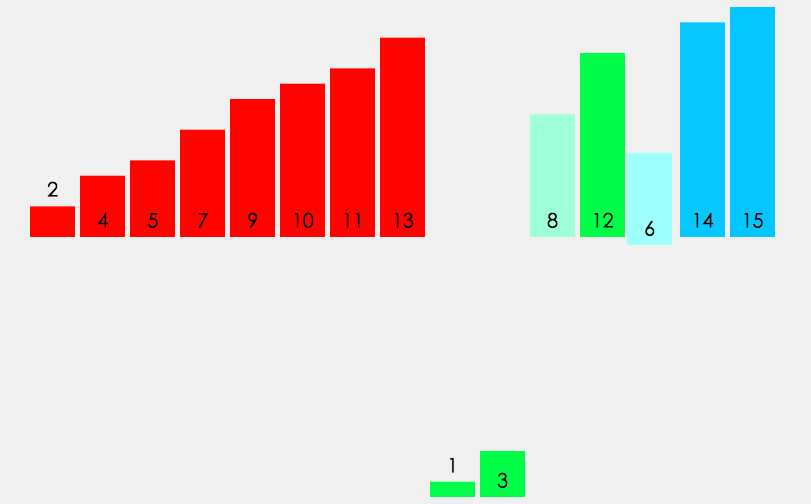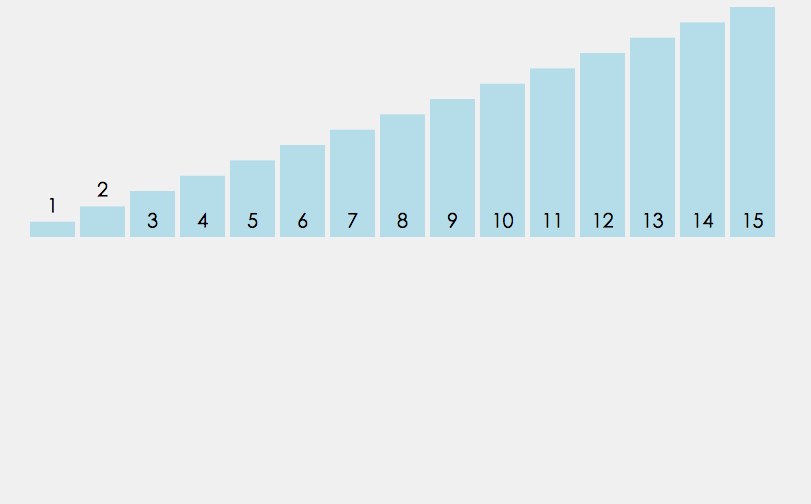
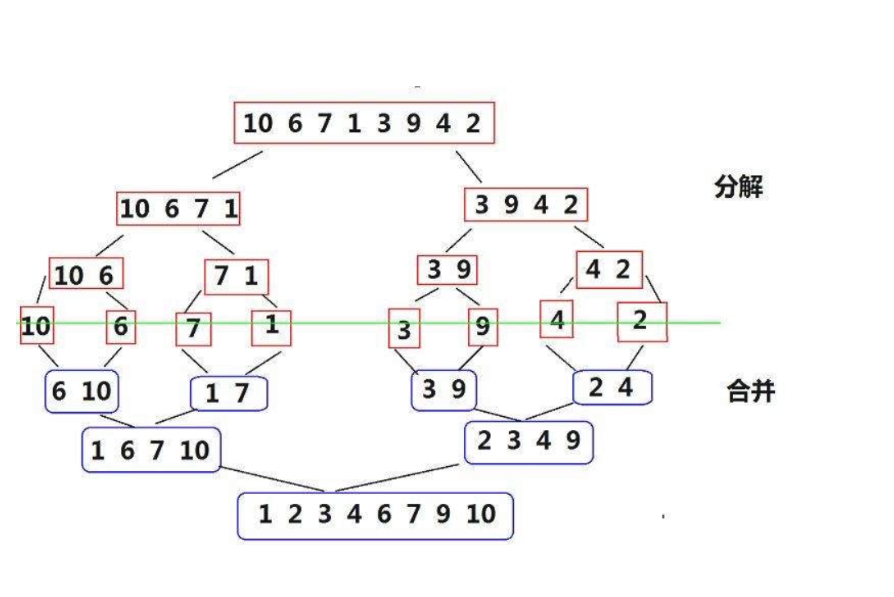
分治递归: 把数组不断对半分,直到只剩一个元素。
双指针合并: 比较两个有序子区间的元素,依次写入临时数组 tmp。
拷贝回原数组: 把排好序的这段 tmp 区间覆盖回原数组对应位置。
解析
1.Merge_Sort 先递归到只剩一个元素,按照顺序依次插入tmp,然后递归回去。
2.比较函数结束后while函数把其余元素继续插入tmp。
3.copy中不能用tmp.end()替代tmp.begin()+right+1.同理tmp.begin()不能替代tmp.begin()+left.
原因:tmp.begin() + right + 1 精确地指定了需要复制的子范围 [left, right] 的结束位置(不包含),这正是copy 函数所需要的。而 tmp.end() 指向的是整个 tmp 向量的末尾,使用它会导致复制的范围过大,从而引发错误。
归并排序(非递归)
初始时,每个元素本身是一个有序段(长度为1)。
每次将"相邻的两个有序段"进行归并。
每轮合并的段长度:1 → 2 → 4 → 8 → ... → n,每次乘2。
不断合并,直到整个数组被合并成一个有序段为止。
一次拷贝
cpp
void Merge_SortNonR1(vector<int>&arr,vector<int>&tmp)
{
int n = arr.size();
for (int gap = 1; gap < n; gap *= 2)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
printf("[%d,%d][%d,%d]", begin1,end1,begin2,end2);
printf(" ");
begin1 = i;
end1 = min(i + gap -1, n - 1);
begin2 = i+gap;
end2 = min(i + 2*gap -1, n - 1);
//修正后
printf("(%d,%d)(%d,%d)", begin1, end1, begin2, end2);
printf(" ");
int j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[j++] = arr[begin1++];
}
else
{
tmp[j++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = arr[begin2++];
}
}
printf("\n");
copy(tmp.begin(), tmp.end(), arr.begin());
}
}没有修正前:
有明显的越界(最大下标该是9) (数组数非二的倍数)

修正方案:
四个元素中除了begin1其余都会越界 -- 分类处理
end1 越界 -- 不归并了(直接拷贝下来)
begin2越界 -- 同end1一样处理
end2越界 -- 继续归并,修正end2
修正路线1
cpp
修正路线
if (end1 >= n)
{
end1 = n - 1;
begin2 = n;//不能修正为n-1 :
end2 = n - 1;
}
else if(begin2 >= n)
{
begin2 = n;
end2 = n - 1;
}
else if (end2 >= n)
{
end2 = n - 1;
}修正路线2
cpp
begin1 = i;
end1 = min(i + gap -1, n - 1);
begin2 = i+gap;
end2 = min(i + 2*gap -1, n - 1);修正后:

修正总结
| 情况 | 修正 | 原因 |
|---|---|---|
end1 >= n |
end1 = n - 1; begin2 = n; end2 = n - 1 |
整个右区间都不存在,强行跳过 |
begin2 >= n |
begin2 = n; end2 = n - 1 |
同上,只是左区间正常,右区间没了 |
end2 >= n |
end2 = n - 1 |
右区间部分存在,尾部越界,修正到最后一位 |
❌ 写成 begin2 = n - 1 |
不安全! | 会误入 begin2 <= end2 逻辑,导致访问非法元素 |
多次拷贝
cpp
void Merge(vector<int>& arr,int left,int mid,int right,vector<int>&tmp)
{
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int i = left;
printf("(%d,%d)(%d,%d)", begin1, end1, begin2, end2);
printf(" ");
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] < arr[begin2])
{
tmp[i++] = arr[begin1++];
}
else
{
tmp[i++] = arr[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
//copy(tmp.begin(), tmp.begin() + right + 1, arr.begin());
for (int j = left; j <= right; j++)
{
arr[j] = tmp[j];
}
}
//归并部分+拷贝部分
void Merge_SortNonR2(vector<int>&arr,vector<int>&tmp)
{
int n = arr.size();
for (int gap = 1; gap < n; gap *= 2)
{
for (int i = 0; i < n; i += 2 * gap)
{
int left = i;//等价于begin1
int mid = i + gap - 1;//等价于end1 begin2 = mid+1
int right = i + gap * 2 - 1;//等价于end2
if (mid >= n || mid+1 >= n)
{
break;
}
if (right >= n)
{
right = n - 1;
}
Merge(arr, left, mid, right, tmp);
}
printf("\n");
}
}修正前:

修正方案1
cpp
if (mid >= n || mid+1 >= n)
{
break;
}
if (right >= n)
{
right = n - 1;
}修正方案2
cpp
mid = min(i + gap - 1,n - 1);
right = min(i + gap * 2 - 1,n - 1);修正后:

多次拷贝和一次拷贝分析
| 比较项 | 多次拷贝 | 一次拷贝 |
|---|---|---|
| 拷贝次数 | 每次归并都 拷贝两次(去 + 回) |
每轮归并只拷贝一次(两个数组交替用) |
| 代码结构 | 简单清晰,易于理解 | 稍复杂,需要维护"轮次+数组切换"逻辑 |
| 内存使用 | 一个临时数组 | 两个数组(原数组 + 临时数组) |
| 性能 | 相对慢(大量重复拷贝) | 更快,避免了不必要的重复拷贝 |
| 稳定性 | 稳定 | 稳定 |
| 适合场景 | 学习、递归模拟 | 追求效率、实际工程 |
归并排序特点
归并排序是一种 分治法(Divide and Conquer)思想的排序算法。它的基本思路是:
分解(Divide):将待排序的数组分成两半,递归地对这两半进行排序。
合并(Merge):将两个已经排序好的子数组合并成一个大的有序数组。
算法步骤
分解:递归地将数组从中间分成两半,直到每个子数组的元素个数为 1。
合并:通过比较两个子数组的元素,将它们合并为一个有序的数组,直到所有元素都被合并成一个整体。
归并排序的特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
- 时间复杂度:O(N*logN)
- 空间复杂度:O(N)
- 稳定性:稳定
总结
下文视情况而定