机器学习④【算法详解：从决策树到随机森林】

文章目录

先言
[一、决策树（Decision Tree）](#一、决策树（Decision Tree）)
- 1.基本概念：树形结构，基于特征进行数据节点划分。
- - 1.1树形结构
  - 1.2特征节点划分原理
- 2.核心算法：ID3、CART（分类与回归树）
- - [2.1基于信息增益决策树的建立ID3（Iterative Dichotomiser 3）](#2.1基于信息增益决策树的建立ID3（Iterative Dichotomiser 3）)
  - 2.2基于基尼指数决策树的建立（CART）
- 3.使用Python的scikit-learn实现决策树对红酒数据进行预测。
[二、集成学习（Ensemble Learning）](#二、集成学习（Ensemble Learning）)
- 1.核心机制：Bagging（自助采样）和随机特征选择。
- 2.随机森林：集成多个决策树，通过投票或平均提高泛化能力。
结语

先言

在人工智能和机器学习领域，选择合适的算法对模型的性能至关重要。今天，我们将深入探讨两种强大且广泛应用的算法------决策树（Decision Tree）和随机森林（Random Forest）。

决策树以其直观的可解释性和简单的逻辑深受欢迎，而随机森林则通过集成学习（Ensemble Learning）进一步提升预测能力，成为许多数据科学竞赛中的"常胜将军"。本文将详细介绍它们的原理、优缺点、应用场景，并通过实例帮助大家理解其工作机制。

无论你是机器学习初学者，还是希望巩固知识的从业者，这篇文章都将为你提供清晰的指导！

一、决策树（Decision Tree）

决策树（Decision Tree）是一种常用的机器学习算法，广泛应用于分类和回归问题。

决策树通过树状结构来表示决策过程，每个内部节点代表一个特征或属性的测试，每个分支代表测试的结果，每个叶节点代表一个类别或值。

1.基本概念：树形结构，基于特征进行数据节点划分。

1.1树形结构

节点（Node）：树中的每个点称为节点。根节点是树的起点，内部节点是决策点，叶节点是最终的决策结果。
分支（Branch）：从一个节点到另一个节点的路径称为分支。
分裂（Split）：根据某个特征将数据集分成多个子集的过程。
纯度（Purity）：衡量一个子集中样本的类别是否一致。纯度越高，说明子集中的样本越相似。

1.2特征节点划分原理

决策树通过递归地将数据集分割成更小的子集来构建树结构。具体步骤如下：

选择最佳特征：根据某种标准（如信息增益、基尼指数等）选择最佳特征进行分割。
分割数据节点：根据选定的特征将数据集分成多个子集。
递归构建子树：对每个子集重复上述过程，直到满足停止条件（如所有样本属于同一类别、达到最大深度等）。
生成叶节点：当满足停止条件时，生成叶节点并赋予类别或值。

2.核心算法：ID3、CART（分类与回归树）

在决策树算法中，ID3 和 CART 是两种经典的构建方法，它们在核心思想、适用场景和优化目标上有所不同。

2.1基于信息增益决策树的建立ID3（Iterative Dichotomiser 3）

信息增益决策树倾向于选择取值较多的属性，在有些情况下这类属性可能不会提供太多有价值的信息，算法只能对描述属性为离散型属性的数据集构造决策树。

基本概念

提出者：Ross Quinlan（1986年）

用途：分类任务（不支持回归）

核心思想：通过信息增益（Information Gain）选择最优特征进行节点分裂，递归构建树。

关键公式

特点

优点：直观易理解，适合离散特征。
缺点：只能处理分类问题，无法直接用于回归，对取值多的特征有偏好（信息增益倾向于选择取值多的特征），无剪枝策略，容易过拟合。
计算示例：
根据以下信息构建一棵预测是否贷款的决策树。我们可以看到有4个影响因素：职业，年龄，收入和学历。

	职业	年龄	收入	学历	是否贷款
1	工人	36	5500	高中	否
2	工人	42	2800	初中	是
3	白领	45	3300	小学	是
4	白领	25	10000	本科	是
5	白领	32	8000	硕士	否
6	白领	28	13000	博士	是

计算步骤：
第一步,计算根节点的信息熵

上表根据是否贷款把样本分成2类样本，"是"占4/6=2/3, "否"占2/6=1/3,

所以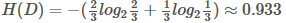
第二步,计算属性的信息增益

<1> "职业"属性的信息增益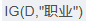

在职业中，工人占1/3, 工人中，是否代款各占1/2, 所以有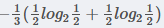

在职业中，白领占2/3, 白领中，是贷款占3/4, 不贷款占1/4, 所以有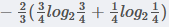

所以有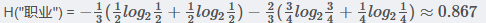

最后得到职业属性的信息增益为：

<2>" 年龄"属性的信息增益（以35岁为界）

<3> "收入"属性的信息增益（以10000为界,大于等于10000为一类）

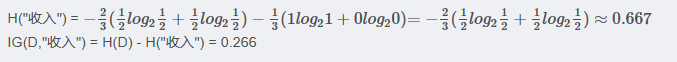
<4> "学历"属性的信息增益（以高中为界, 大于等于高中的为一类）

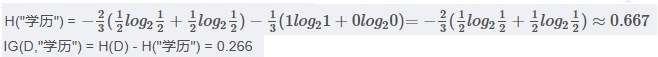
第三步, 划分属性

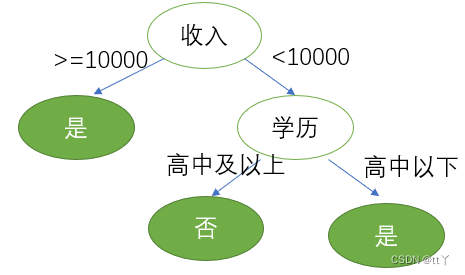
对比属性信息增益发现，"收入"和"学历"相等，并且是最高的，所以我们就可以选择"学历"或"收入"作为第一个

决策树的节点，接下来我们继续重复1，2的做法继续寻找合适的属性节点

2.2基于基尼指数决策树的建立（CART）

基尼指数 （Gini Index）是决策树算法中用于评估数据集纯度的一种度量，基尼指数衡量的是数据集的不纯度，或者说分类的不确定性。在构建决策树时，基尼指数被用来决定如何对数据集进行最优划分，以减少不纯度。

基本概念

提出者：Breiman等（1984年）

用途：分类和回归（支持两者）

核心思想：分类任务：使用基尼系数（Gini Index）选择特征；回归任务：使用均方误差（MSE）选择分裂点。

关键公式

Gini指数的计算和上述信息增益相似我们直接进入案例

3.使用Python的scikit-learn实现决策树对红酒数据进行预测。

示例代码：

python 复制代码

from sklearn.tree import DecisionTreeClassifier,export_graphviz
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import  StandardScaler
# 创建数据集
wine = load_wine()
x = wine.data
y = wine.target
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)
#创建决策数模型对象
# criterion="entropy"表示使用信息熵作为划分标准(默认gini:gini系数划分标准)
model = DecisionTreeClassifier(criterion="gini",max_depth=None)
#对数据集新型标准化
transfer = StandardScaler()
x_train = transfer.transform(x_train)
X_test = transfer.transform(x_test)
#训练模型
model.fit(x_train,y_train)
#保存模型
# joblib.dump(model,"../src/model/DecisionTree.pkl")
#模型预测
y_predict = model.predict(X_test)
print("预测结果为：",y_predict)
#f返回预测准确率
score = model.score(X_test,y_test)
print("预测准确率：",score)
#可视化决策树模型
export_graphviz(model,out_file="../src/graph/DecisionTree.dot",feature_names=wine.feature_names)

二、集成学习（Ensemble Learning）

机器学习中有一种大类叫集成学习 （Ensemble Learning），集成学习的基本思想就是将多个分类器组合，从而实现一个预测效果更好的集成分类器。集成算法可以说从一方面验证了中国的一句老话：三个臭皮匠，赛过诸葛亮。集成算法大致可以分为：Bagging，Boosting 和 Stacking 三大类型。

（1）每次有放回地从训练集中取出 n 个训练样本，组成新的训练集；

（2）利用新的训练集，训练得到M个子模型；

（3）对于分类问题，采用投票的方法，得票最多子模型的分类类别为最终的类别；

1.核心机制：Bagging（自助采样）和随机特征选择。

Bagging（Bootstrap Aggregating）是一种集成学习（Ensemble Learning）方法，通过组合多个弱学习器的预测结果来提升模型的稳定性和泛化能力。其核心思想是：通过自助采样（Bootstrap Sampling）生成多个子数据集，并行训练多个基学习器，最终通过投票（分类）或平均（回归）得到最终预测。
Bagging 的核心步骤：

2.随机森林：集成多个决策树，通过投票或平均提高泛化能力。

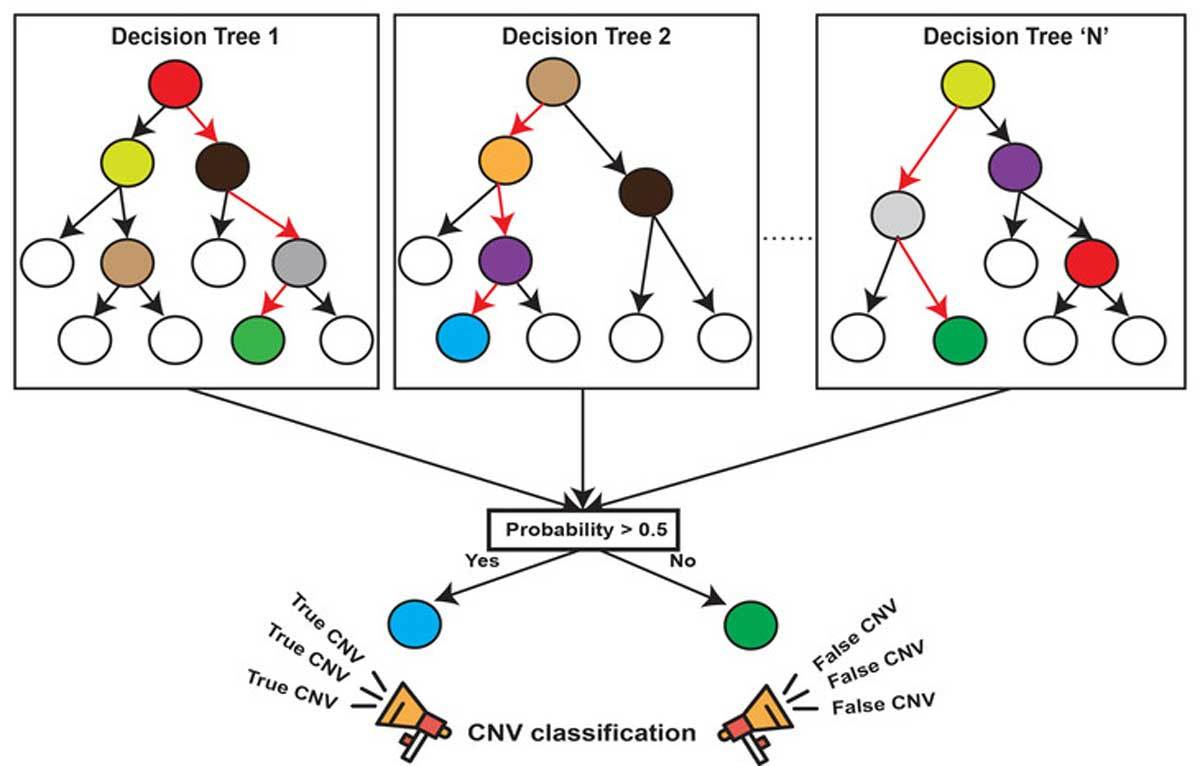
随机森林 就属于集成学习,是通过构建一个包含多个决策树(通常称为基学习器或弱学习器)的森林，每棵树都在不同的数据子集和特征子集上进行训练，最终通过投票或平均预测结果来产生更准确和稳健的预测。这种方法不仅提高了预测精度，也降低了过拟合风险，并且能够处理高维度和大规模数据集
随机森林是 Bagging 的扩展，在决策树的基础上增加了特征随机性：

随机: 特征随机，训练集随机
- 样本：对于一个总体训练集T，T中共有N个样本，每次有放回地随机选择n个样本。用这n个样本来训练一个决策树。
- 特征：假设训练集的特征个数为d，每次仅选择k(k<d)个来构建决策树。
森林: 多个决策树分类器构成的分类器, 因为随机，所以可以生成多个决策树

复制代码

class sklearn.ensemble.RandomForestClassifier

参数：

n_estimators int, default=100

森林中树木的数量。(决策树个数)

criterion {"gini", "entropy"}, default="gini" 决策树属性划分算法选择

当criterion取值为"gini"时采用基尼不纯度（Gini impurity）算法构造决策树，

当criterion取值为 "entropy" 时采用信息增益（ information gain）算法构造决策树.

max_depth int, default=None 树的最大深度。

示例代码：

python 复制代码

from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
import joblib
transfer = joblib.load("../src/model/transfer.pkl")
wine = load_wine()
X_train,X_test,y_train,y_test = train_test_split(wine.data,wine.target,test_size=0.2,random_state=42)
#创建随机森林模型n_estimators参数指定创建100棵树
model_forest = RandomForestClassifier(n_estimators=100,criterion="gini",max_depth=None)
#对数据进行标准化
X_train = transfer.transform(X_train)
X_test = transfer.transform(X_test)
#使用模型进行训练
model_forest.fit(X_train,y_train)
#预测
y_predict = model_forest.predict(X_test)
print("预测结果为：",y_predict,"实际结果为：",y_test)
#预测准确度
score = model_forest.score(X_test,y_test)
print("准确度为：",score)

结语

决策树和随机森林是机器学习中不可或缺的工具，理解它们的原理和应用能帮助我们在实际项目中做出更优的模型选择。接下来的内容将深入技术细节，并附上代码示例，敬请期待！

🔍 你对决策树或随机森林有什么疑问？欢迎在评论区留言讨论！

📌 下一篇预告：我们将深入探讨线性回归以及如何梯度下降求解理想损失函数！