文章目录
-
- 一.分类分析算法
- 二.聚类分析
-
- 1.聚类分析
- 2.相关概念
-
- [2.1 数据样本X](#2.1 数据样本X)
- [2.2 数据样本集](#2.2 数据样本集)
- [2.3 簇C_j](#2.3 簇C_j)
- [2.4 数据结构](#2.4 数据结构)
-
- [2.4.1 数据矩阵](#2.4.1 数据矩阵)
- [2.4.2 相异矩阵](#2.4.2 相异矩阵)
- [2.5 聚类中的属性类型](#2.5 聚类中的属性类型)
- 3.相异性度量(距离)
-
- [3.1 欧式距离](#3.1 欧式距离)
-
- [3.1.1 欧几里德距离](#3.1.1 欧几里德距离)
- [3.1.2 标准化欧氏距离](#3.1.2 标准化欧氏距离)
- [3.1.3 加权欧氏距离](#3.1.3 加权欧氏距离)
- [3.2 曼哈顿距离](#3.2 曼哈顿距离)
- [3.3 切比雪夫距离](#3.3 切比雪夫距离)
- [3.4 闵可夫斯基距离](#3.4 闵可夫斯基距离)
- [3.5 距离度量的性质](#3.5 距离度量的性质)
- 4.余弦相似度
-
-
- [4.1 余弦相似度](#4.1 余弦相似度)
- [4.2 调整余弦相似度](#4.2 调整余弦相似度)
-
- [5. 二元变量(属性)相异性](#5. 二元变量(属性)相异性)
-
- [5.1 二元变量(属性)匹配情况表格](#5.1 二元变量(属性)匹配情况表格)
- [5.2 对称二元变量](#5.2 对称二元变量)
- [5.3 不对称二元变量](#5.3 不对称二元变量)
- 6.标称变量(属性)相异性
-
-
- [6.1 简单匹配方法](#6.1 简单匹配方法)
- [6.2 使用二元变量编码](#6.2 使用二元变量编码)
-
- 7.序列型变量的相异性
- 8.簇间的距离度量标准
-
- [8.1 簇间的距离度量标准](#8.1 簇间的距离度量标准)
- [8.2 聚类准则函数](#8.2 聚类准则函数)
- [9. 聚类挖掘](#9. 聚类挖掘)
-
- [9.1 分层聚类](#9.1 分层聚类)
- [9.2 K-means聚类](#9.2 K-means聚类)
- [9.3 DBSCAN聚类](#9.3 DBSCAN聚类)
一.分类分析算法
1.分类分析
分类分析的基本思想是先将大量数据分为若干个类别,再分别分析每个类别的统计特征,通过每个类别的统计特征反映数据总体的特征
2.决策树
2.1 决策树思想与实现
决策树与人们对动物的树形分类方法类似,分类过程是通过递归方式 进行的,每次分类都基于:最显著属性进行划分

决策树实现方法有很多:
- ID3
- C4.5
- C5.0
- 分类和回归树(Classification and Regression Tree, C&R Tree)
- 卡方自动交互检验法(Chi-squared Automatic Interaction Detector,CHAID)
2.2 决策树构造
2.2.1 节点选择?
第一个问题就是如何切分特征(选择节点)
- 根节点的选择用那个特征呢?接下来呢?如何切分呢?

我们的目标就是通过一种衡量标准,来计算通过不同特征进行分支选择后的分类情况,找出来最好的那个当成根节点,以此类推
2.2.2 信息熵
信息量的定义
若一个消息X出现的概率为p,则这一消息所含的信息量为
I = − log 2 p I = -\log_2 p I=−log2p
Eg.
抛一枚均匀硬币,出现正面与反面的信息量是多少
I(正)= I(反)=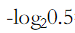 = 1bit
= 1bit
抛一枚畸形硬币,出现正面与反面的概率分别是1/4,3/4,出现正面与反面时的信息量是多少?
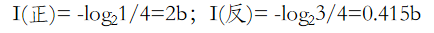
信息熵
信源含有的信息量是信源发出的所有可能消息的平均不确定性
信源(比如抛硬币的结果)包含的 "平均不确定性"。简单说,就是 "猜这个结果有多难"------ 不确定性越大,信息熵越高。
信息论创始人香农 把信源所含有的信息量称为信息熵(entropy),是指每个符号所含信息量的统计平均值。m种符号的平均信息量为:
H ( X ) = ∑ i = 1 m p ( x i ) I ( x i ) = − ∑ i = 1 m p ( x i ) log 2 p ( x i ) H(X) = \sum_{i=1}^m p(x_i)I(x_i) = -\sum_{i=1}^m p(x_i)\log_2 p(x_i) H(X)=i=1∑mp(xi)I(xi)=−i=1∑mp(xi)log2p(xi)

Eg.抛一枚均匀硬币的信息熵:
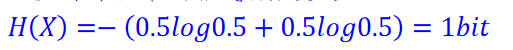
Eg.抛一枚畸形硬币,出现正面与反面的概率分别是1/4,3/4,出现正面与反面时的信息熵
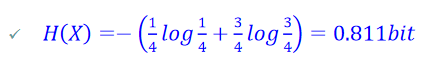
2.2.3 ID3算法
ID3算法:选择最优分裂属性:信息增益
D在属性A上分裂后,标识各个元组所需信息量减少多少,用信息增益(Information Gain)来表示(信息量越来越少,不确定性越来越低)
G a i n ( A ) = I n f o ( D ) − I n f o A ( D ) Gain(A) = Info(D) - Info_A(D) Gain(A)=Info(D)−InfoA(D)
ID3算法选择信息增益最大的属性作为当前的分类属性
这样做使得目前要完成最终分类所需的信息量最小
ID3 选择信息增益最大的属性分裂,是为了当前步骤最大化 "信息量减少" ,从而加快分类过程;但由于是贪心策略,它无法保证得到全局最优的决策树,可能会因为局部最优的选择而陷入 "次优解"
Eg1.
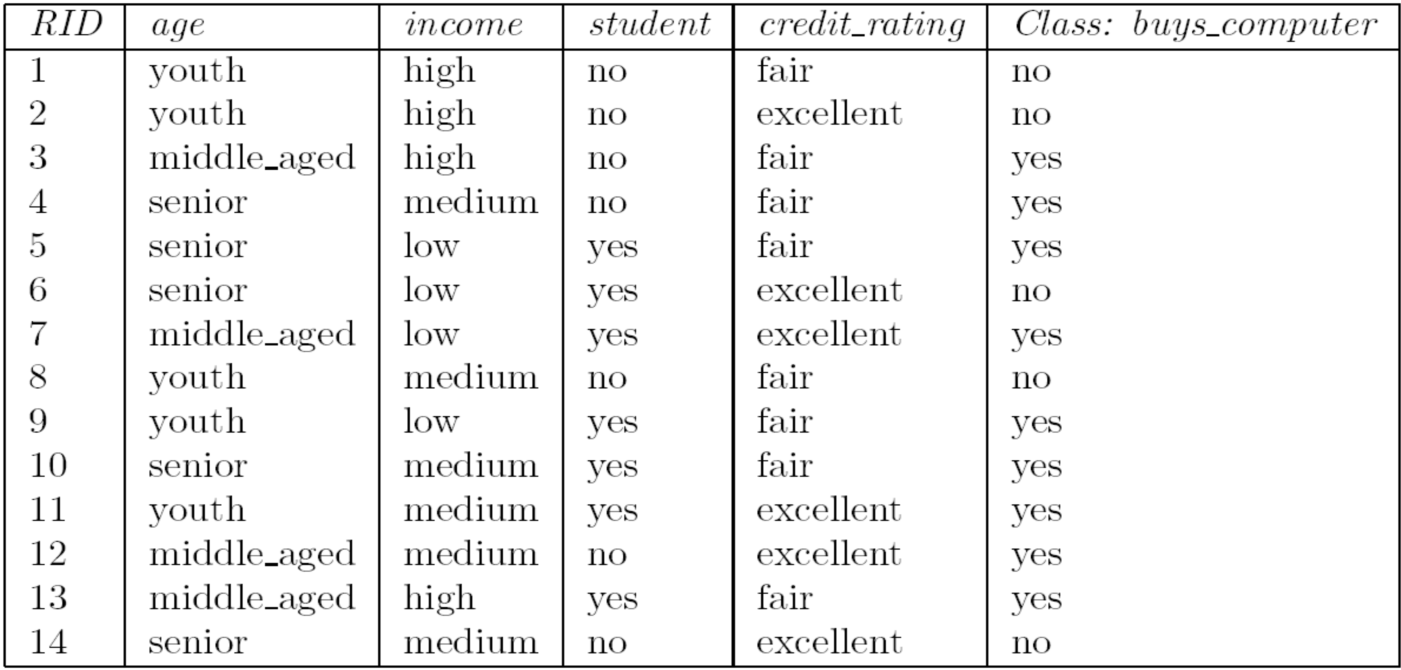
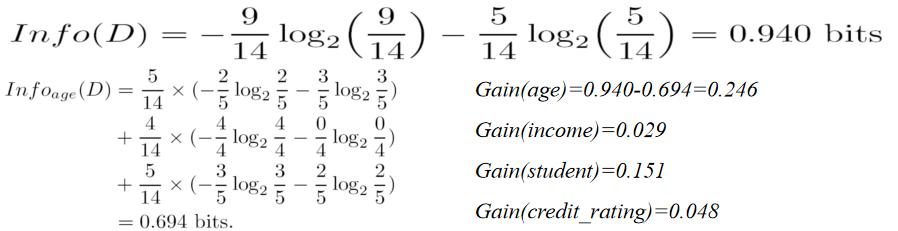
- 总样本数 (N = 14)
yes的样本数:第 3、4、5、7、9、10、11、12、13 行,共 9 个;no的样本数:第 1、2、6、8、14 行,共 5 个。
- 计算根节点的总熵
- 计算每个属性的信息增益
- 选择信息增益最大的属性为根结点
- 对根节点的每个分支递归建树

注意:分支age=middle_aged该分支下所有样本buys_computer=yes(纯类别),因此该分支直接生成叶节点yes。
通过 "选择最优属性→递归分支→生成叶节点" 的过程,就完成了决策树的构建。
Eg2.是否适合打垒球的决策表
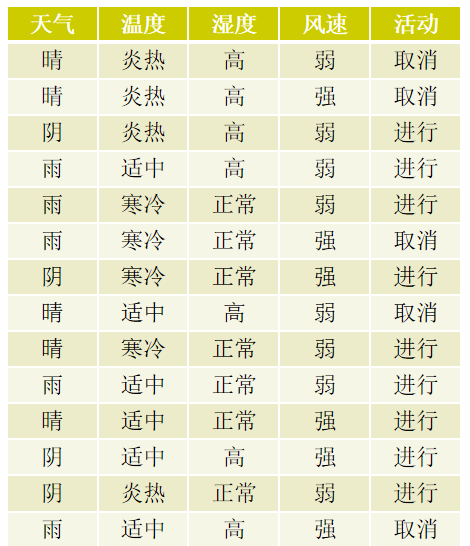
先验熵:在没有接收到其它任何属性值时候,活动进行与否的熵
H(活动) = - (9/14)*log (9/14) - (5/14)*log (5/14) = 0.94
这个熵值反映了 "活动是否进行" 的初始不确定性(熵越大,不确定性越高)。
信息增益的核心是 "某个属性能让'活动是否进行'的不确定性降低多少"。
比如接下来会分析 "天气""温度""湿度""风速" 这些属性,分别计算它们的 "条件熵",再用 "先验熵 - 条件熵" 得到信息增益。信息增益越大,说明该属性对决策的 "区分能力" 越强,越适合作为决策树的节点。
3.贝叶斯定理(Bayes theorem )
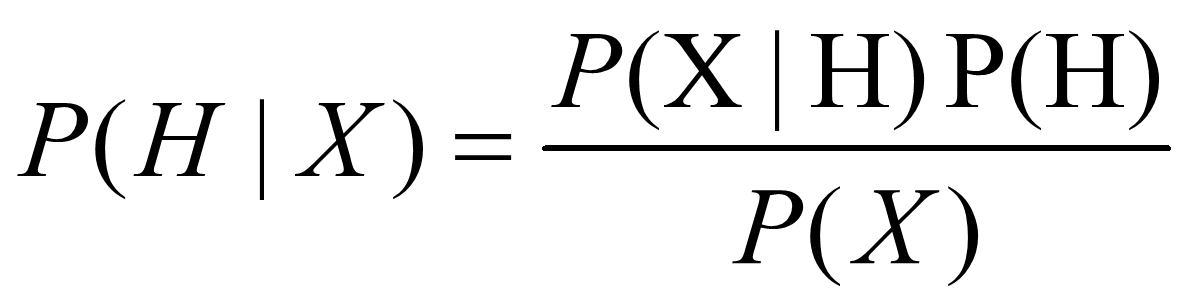
3.1 朴素贝叶斯分类
有m个分类: C1, C2, ......, Cm
每个数据样本用一个n维特征向量X= {x1,x2,......,xn}表示,分别描述对n个属性A1,A2,......,An样本的n个度量。
给定一个未知的数据样本X(即没有类标号),分类器将预测X属于具有最高后验概率(条件X下)的类。
朴素贝叶斯分类将未知的样本分配给类Ci ,当且仅当:
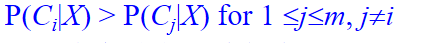
P(Ci|X)称为最大后验假定。
后验概率的公式是 (P(C_i | X)) ------"已知特征 X 时,属于类 (C_i) 的概率"。
根据贝叶斯定理
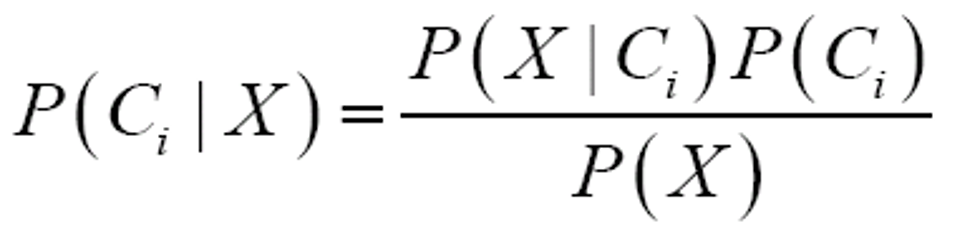

由于P(X)对于所有类为常数,只需要P(X|Ci)P(Ci)最大即可
类的先验概率可以用:P(Ci)=Si/S,其中Si是类Ci中的训练样本数,而S是训练样本总数
- 分类逻辑 :对一个样本(比如某封邮件),计算它属于每一类(垃圾 / 非垃圾)的后验概率,概率最大的类别就是分类结果。比如算出来 "含折扣的邮件是垃圾邮件的概率是 80%,非垃圾的概率是 20%",就把它归为垃圾邮件。
- 朴素贝叶斯的 "朴素" 之处 :假设特征之间相互独立(比如 "含折扣" 和 "含免费" 这两个特征,在垃圾邮件里的出现互不影响)。这是为了简化计算,让算法能高效处理高维特征。
如何计算P(X|Ci)?现在是一个问题
类条件独立的朴素假定(class conditional independence ):
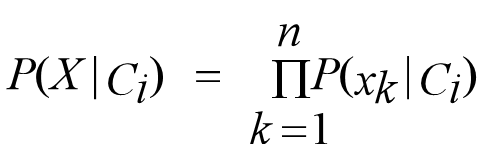
如果 Ak是离散值,则P(xk|Ci)=Sik/Si,Sik是D中类别为Ci且属性Ak取值为xk的元组个数;SiD中属于Ci 类别的元组数量;如果属性 Ak是连续值类型,假设符合高斯分布(Gaussian distribution):
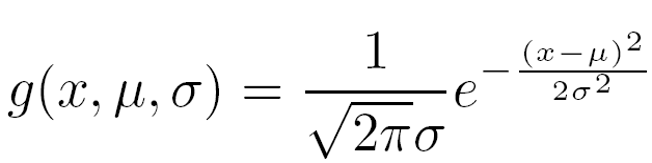
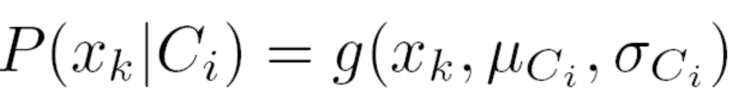
Eg.
分类:
C1:buys_computer='yes' C2:buys_computer='no'
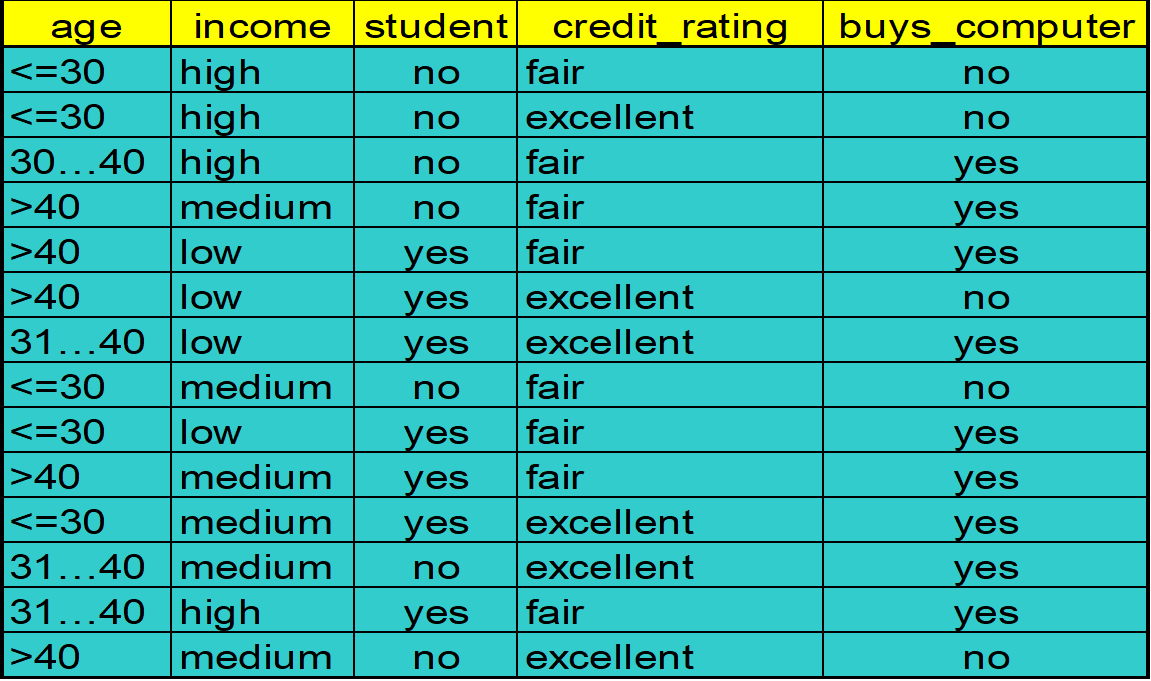
X =(age<=30, Income=medium, Student=yes,Credit_rating=Fair)会不会买电脑?
- 明确目标与特征
- 计算先验概率
- 计算条件概率
- 用朴素贝叶斯公式预测

3.2 优点与缺点
- 优点
- 朴素贝叶斯模型发源于古典数学理论,有较高的分类效率
- 对于小规模的数据表现很好,能处理多分类任务,适合增量式训练
- 对缺失数据不敏感,算法也比较简单
"能处理多分类任务":就是可以同时区分多个类别。比如不仅能分 "垃圾邮件 / 非垃圾邮件",还能分 "新闻 / 科技 / 娱乐" 等多个类别。
"适合增量式训练":指算法可以 "边加数据边训练"。比如新来了一批样本,不用把旧数据全丢了重新训练,直接把新数据加进去更新模型就行,很灵活。
- 缺点
- 模型假设属性之间相互独立,在实际应用中往往不成立。在属性个数比较多或者属性之间相关性比较大时,分类效果不好。而在属性相关性较小时,不俗贝叶斯性能最为良好
- 需要知道先验概率。且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳
- 通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率
3.3 贝叶斯网络
贝叶斯网络的网络结构是一个有向无环图(Directed Acyclic Graph,DAG),由结点和有向边组成。每个结点代表一个"事件"或者"随机变量",而有向边表示随机变量的"条件依赖"。表示起因的假设和表示结果的数据均用结点表示,如图
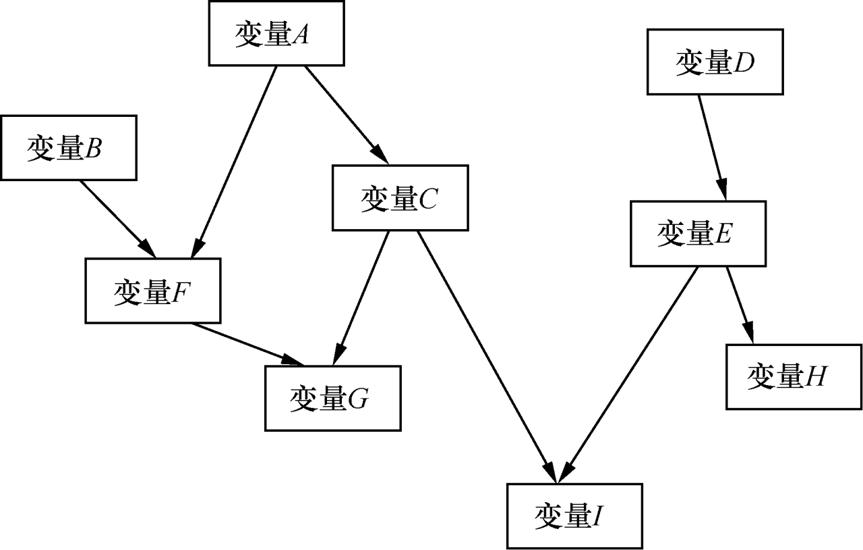
- 变量 A :是变量 C 和变量 F 的 "父节点",即变量 C 和 F 的概率分布条件依赖于 A。
图神经网络(GNN)最适合处理的核心数据结构是 图(Graph),即包含 "实体(节点)+ 实体间关联(边)" 的非规则 / 关联数据(如社交网络、知识图谱、分子结构等)。
二.聚类分析
1.聚类分析
簇:由彼此相似的一组对象所构成的集合称为簇
- 同一个簇内的数据是相似的
- 不同簇之间的数据是相异的
聚类分析:将一组数据对象划分为若干个簇
- 聚类分析是一种无指导的分类,即无预先定义的类
聚类分析应用领域
- 可以帮助营销人员发现客户中所存在的不同特征的组群
- 从卫星遥感图像数据中识别具有相似土地使用情况的区域
- 可以作为一个独立的工具使用,可以进行数据的预处理、分析数据的分布、了解各种数据的特征、作为其他数据挖掘功能的辅助手段。
什么是一个好的聚类:一个好的聚类方法产生具有如下性质的簇
- 类内:数据项之间有高相似性
- 类间:数据项之间有低相似性
2.相关概念
2.1 数据样本X
X = (x1, x2, ..., xd),其中x_i表示样本中的各个属性,d是样本或样本空间的维数(或属性个数)
2.2 数据样本集
记作{X1,X2,...,Xn}, 第i个样本记为Xi={xi1,...,xid}
2.3 簇C_j
-
数据样本集被分成k个簇,每个簇是相应数据样本的集合,相似样本在同一簇中,相异样本在不同簇中。
-
簇的质心(centroid):样本的平均值,是簇的"中间值",但并不需要是簇中实际点
令ni表示簇Ci中样本的数量,mi表示对应样本的均值:
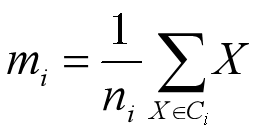
2.4 数据结构
2.4.1 数据矩阵
在很多情况下,聚类的样本集看成是一个n×p的数据矩阵
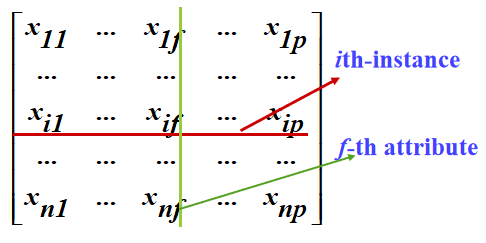
行代表样本(instance),列代表属性(attribute)
2.4.2 相异矩阵
描述n个样本两两之间的相异性
d(Xi,Xj)是样本Xi和样本Xj间相异性的量化表示
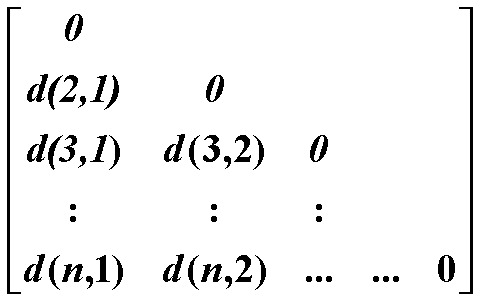
- 矩阵的行和列都对应样本(共n个样本,矩阵维度为(n × n))。
- 单元格\d(i,j)\表示样本(X_i)和样本(X_j)之间的相异度(数值越大,差异越大)。
- 对角线元素都是 0(因为 "样本自己和自己的差异为 0")。
- 矩阵是对称的d(i,j) = d(j,i),比如样本 1 和样本 2 的差异,与样本 2 和样本 1 的差异是一样的
2.5 聚类中的属性类型
不同类型的属性需要使用不同的相异性度量
-
Interval-scaled variables 区间标度变量:是一个粗略线性标度的连续度量
比如身高(160cm、170cm)、温度(25℃、30℃)。衡量差异时,常用 "数值差的大小",比如两个人身高差 5cm,就代表一定的相异性。
-
Binary variables 二元变量:只有两个值:0、1
比如 "是否已婚"(0 = 未婚,1 = 已婚)。差异度量看是否相同,相同则差异小(比如两个都是 1,差异为 0),不同则差异大(一个 0 一个 1,差异为 1)。
-
Nominal (Categorical), ordinal, and ratio variables 标称型、序数型和比例标度型变量
**标称型:**类别型,无顺序,比如 "颜色(红、蓝、绿)""职业(教师、医生)"。差异度量看是否属于同一类,同一类差异小,不同类差异大
**序数型:**有顺序的类别,比如 "学历(小学、中学、大学)"。差异不仅看是否同类,还看顺序的远近,比如小学和大学的差异比小学和中学大。
**比例标度型:**是有绝对零点的区间变量,比如收入(0 元代表没有收入)。差异度量类似区间变量,但能体现 "比例",比如收入 1000 元和 2000 元的差异,与 2000 元和 4000 元的差异在比例上是一致的。
-
Variables of mixed types 混合类型
数据集里同时有多种类型的属性,比如既有 "身高(区间型)" 又有 "婚姻状况(二元型)"。这时候需要对不同类型的属性分别选对应的差异度量,再综合起来计算整体相异性。
3.相异性度量(距离)
3.1 欧式距离
3.1.1 欧几里德距离
Xi{xi1,...,xin}和Xj{xj1,...,xjn}是两个具有n个属性的两个样本。距离度量标准d(Xi, Xj)表示第i个样本与第j个样本间的距离。
在聚类分析中,最常用的距离度量标准是d维空间中的欧几里德距离:
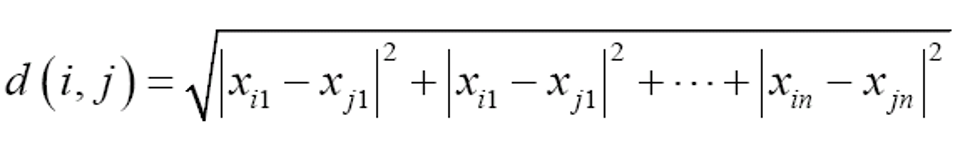
- 定义了多维空间之间点与点之间的"直线距离"
- 具有空间旋转不变性
- 需要保持各个维度指标在相同的刻度级别
- 注重各个对象的特征在数值上的差异,用于从维度的数值大小中分析个体差异
- "定义了多维空间之间点与点之间的'直线距离'":不管是 2 维(平面)、3 维(空间)还是更多维,欧氏距离都是 "把每个维度的差值算平方和,再开根号",就像在高维空间里画一条直线来量两点的距离。
- "具有空间旋转不变性":比如把坐标系旋转一下(比如从 "东 - 北" 坐标系转到 "东南 - 西北" 坐标系),两点的欧氏距离不会变。这说明它只关心 "实际距离",不关心坐标的方向。
- "需要保持各个维度指标在相同的刻度级别":比如一个维度是 "身高(厘米,0-200)",另一个是 "体重(公斤,0-100)",刻度差异大,直接算欧氏距离会被数值大的维度(身高)主导。所以得先把各维度 "归一化" 到同一刻度(比如都缩放到 0-1 之间)。
- "注重各个对象的特征在数值上的差异,用于从维度的数值大小中分析个体差异":欧氏距离是 "数值差的平方和",数值差异越大,距离越大。比如两个样本的 "收入" 差 1000 和 "年龄" 差 5,欧氏距离会同时考虑这两个差异的综合影响,从而判断个体间的整体差异。
3.1.2 标准化欧氏距离
标准化欧式距离(Standardized Euclidean Distance)由于各个属性的量纲不一致(比如收入和年龄),通常需要先对各属性进行标准化,使其与单位无关
假设样本集X的均值(mean)为m,标准差(standard deviation)为s,那么X的"标准化变量"表示为:(就是Z-score标准化)
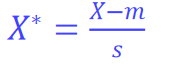
之后在计算欧氏距离
3.1.3 加权欧氏距离
加权欧式距离(Weighted Euclidean distance):在计算距离时,需要考虑各项具有不同的权重
Eg.
计算奥运奖牌榜中各个国家之间的相异性,每一个国家有3 个属性,分别表示获得的金、银、铜牌数
在计算距离时, 把金、银、铜牌所起的作用等同看待,这显然是不合理的
采用加权欧氏距离,使在计算距离时,金、银、铜牌所起的作用依次减小
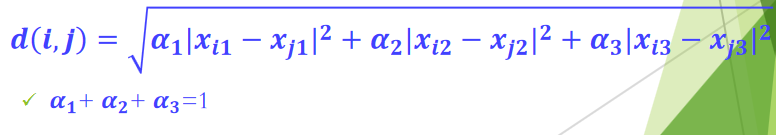
3.2 曼哈顿距离
数值属性的相异性- 曼哈顿距离(Manhattan distance)
想象你在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?
显然不是,除非你能穿越大楼。实际驾驶距离就是这个"曼哈顿距离",是名称的来源,也称为城市街区距离(CityBlock distance)。
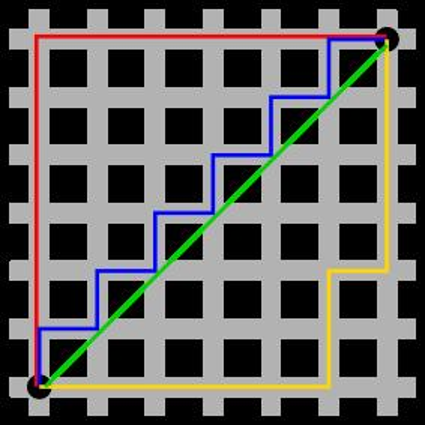
图中红线代表曼哈顿距离,绿色代表欧氏距离,也就是直线距离,而蓝色和黄色代表等价的曼哈顿距离。
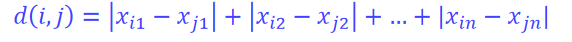
- 2D 场景(比如城市街道):像沿格子路从一点走到另一点,只能横向或纵向移动,总路程就是横向与纵向距离的和。
- 例子:A (2,5) 和 B (7,3),维度差为 | 2-7|=5、|5-3|=2,曼哈顿距离就是 5+2=7。
3.3 切比雪夫距离
数值属性的相异性-切比雪夫距离 ( Chebyshev Distance )
- 2D 场景(比如棋盘):两点横向、纵向距离中的较大值(比如国王走棋,一步能到任意方向,最大步长就是切比雪夫距离)。
- 例子:A (2,5) 和 B (7,3),维度差为 | 2-7|=5、|5-3|=2,切比雪夫距离就是 5。
切比雪夫距离的核心用途是聚焦 "最大维度差异",适合需优先解决极端偏差、忽略累计小差异的场景,具体应用如下:
- 棋盘与游戏场景
- 最经典用途是计算棋盘上两点的最短步数,比如国际象棋的国王、中国象棋的帅 / 将,它们能向任意方向走一步,最短步数就是横向和纵向距离的最大值(即切比雪夫距离)。
3.4 闵可夫斯基距离
Minkowski distance(闵可夫斯基距离)
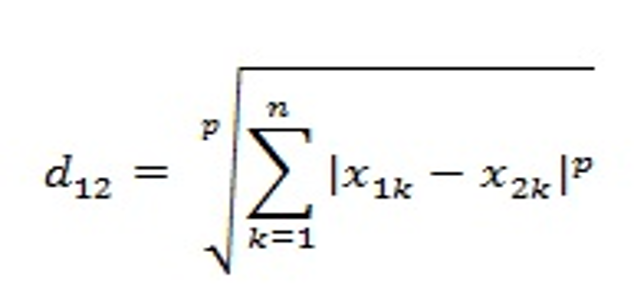

可以给各个属性加权值,表示不同的重要程度:
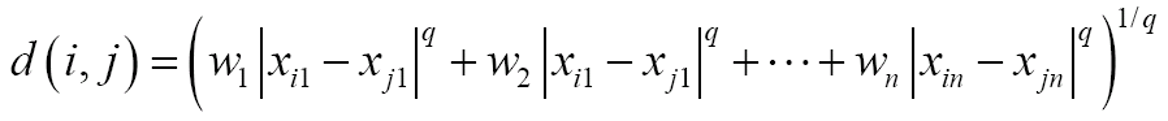
3.5 距离度量的性质
距离度量满足以下要求:
- d(i, j) ≥ 0 距离是一个非负的数值
- d(i, i) = 0 一个对象与自身的距离是 0
- d(i, j) = d(j, i) 距离函数具有对称性
- d(i, j) ≤ d(i, h) + d(h, j) 三角不等式
给出这些性质的关键在于,当我们在同一空间中定义了多个满足这些性质的距离时,这些不同的距离仍然能够在两点之间远的时候就大,近的时候就小
这 4 个性质合起来,能确保不管用哪种距离(欧氏、曼哈顿等),都能一致地用 "数值大 = 远,数值小 = 近" 来判断,不会出现 "甲距离比乙大,但实际甲更近" 的混乱。
如果三角不等式成立,则该性质可以用来提高依赖于距离的技术(包括聚类)的效率。
- 举个聚类的例子:聚类是要把距离近的点归为一类。如果我们已经知道点 A 到点 B 的距离是 10,点 A 到点 C 的距离是 2,根据三角不等式,点 B 到点 C 的距离至少是 8(10-2)。
- 这时候如果我们正在判断 "点 C 要不要和点 B 归为一类",而聚类的阈值是 5(只归距离≤5 的点),那不用计算 B 和 C 的实际距离,就能直接排除 ------ 因为它至少是 8,超过了阈值。
- 简单说:三角不等式能帮我们 "跳过不必要的距离计算",尤其数据量大的时候,能省很多时间,让聚类等依赖距离的技术跑得更快。
4.余弦相似度
4.1 余弦相似度
余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小
相比于距离度量,余弦相似度更注重于两个向量在方向上的差异,而非距离或者长度上
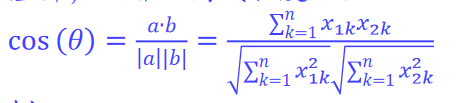
例:
-
当两条新闻向量夹角余弦等于1时,这两条新闻完全重复(用这个办法可以删除爬虫所收集网页中的重复网页)
-
当夹角的余弦值接近于1时,两条新闻相似(可以用作文本分类);夹角的余弦越小,两条新闻越不相关。
4.2 调整余弦相似度
余弦相似度更多的是从方向上区分差异,而对绝对的数值不敏感,因此没法衡量每个维度上数值的差异。
需要修正这种不合理性,就出现了调整余弦相似度,即所有维度上的数值都减去一个均值。
- 普通余弦的问题
比如你打分偏松(4、5、4),朋友打分偏严(2、3、2),两人都觉得第二部最好(趋势一致)。但普通余弦可能因绝对分数差大,没法精准体现这种 "偏好相似"。
- 调整余弦的做法(两步搞定)
- 第一步:算各自均值(打分基准)------ 你均值≈4.33,朋友均值≈2.33。
- 第二步:所有分数减自己的均值 ------ 你变成(-0.33、0.67、-0.33),朋友变成(-0.33、0.67、-0.33)。
- 最后算调整后向量的余弦相似度,结果 = 1,完美匹配 "偏好一致" 的事实。
一句话区别
- 普通余弦:看 "绝对分数的方向"。
- 调整余弦:看 "相对于自己习惯的相对偏好方向"。
例:用户对内容评分,按5分制,X和Y两个用户对两个内容的评分分别为(1,2)和(4,5)使用余弦相似度得到的结果是0.98,两者极为相似。
但从评分上看X似乎不喜欢两个这个内容,而Y则比较喜欢。如果X和Y的评分均值都是3,那么调整后为(-2,-1)和(1,2),再用余弦相似度计算,得到-0.8,相似度为负值并且差异不小,但显然更加符合现实。
结果范围:-1 到 1 之间。1 表示方向完全相同,0 表示垂直无关联,-1 表示方向完全相反。
5. 二元变量(属性)相异性
5.1 二元变量(属性)匹配情况表格
二元变量只有两个状态:0或1(0表示该变量为空,1表示该变量存在)
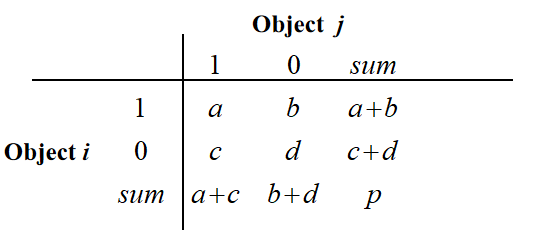
- 区域 a :对象 i 和对象 j 的属性值都为 1的数量。比如两个用户都喜欢 "篮球" 这个属性,就计入 a。
- 区域 b:对象 i 的属性值为 1、对象 j 的属性值为 0 的数量。比如 i 喜欢 "足球",但 j 不喜欢,计入 b。
- 区域 c:对象 i 的属性值为 0、对象 j 的属性值为 1 的数量。比如 i 不喜欢 "网球",但 j 喜欢,计入 c。
- 区域 d :对象 i 和对象 j 的属性值都为 0的数量。比如两个用户都不喜欢 "排球",计入 d。
- p :每个对象的属性总数,即
p = a + b + c + d,代表所有被统计的属性数量。 - 对于 Object i:
- 属性值为 1 的数量是 (a + b),
- 属性值为 0 的数量是 (c + d),
- 因此 Object i 的属性总数是 ((a + b) + (c + d) = a + b + c + d = p)。
Eg.

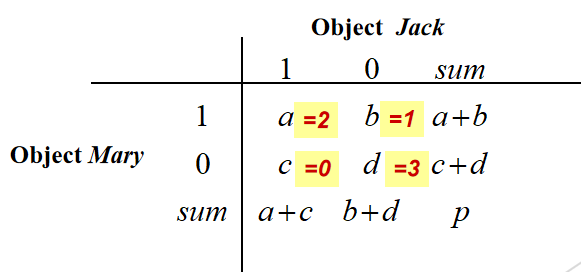
用二进制属性匹配表 来分析 Jack 和 Mary 在 6 个属性(Fever、Cough、Test-1 到 Test-4)上的相似性,核心是通过a、b、c、d四个区域统计属性的匹配情况
| (a=2) | 两人都有的属性数量 | Fever(都 Y)、Test-1(都 P)→ 共 2 个 |
|---|---|---|
| (b=1) | Mary 有、但 Jack 没有的属性数量 | Test-3(Mary 是 P,Jack 是 N)→ 共 1 个 |
| (c=0) | Jack 有、但 Mary 没有的属性数量 | 没有这种情况 → 0 个 |
| (d=3) | 两人都没有的属性数量 | Cough(都 N)、Test-2(都 N)、Test-4(都 N)→ 共 3 个 |
属性总数 (p = a + b + c + d = 2 + 1 + 0 + 3 = 6),和上方表格的 "P=6" 一致,说明统计是对的。
5.2 对称二元变量
如果"0"和"1"两个个状态是同等价值的,并有相同的权重,则该二元变量是对称的
- 例如,性别,两个取值"0"和"1"没有优先权。基于对称二元变量的相似度称为恒定的相似度。采用简单匹配系数评价两个对象之间的相异度:
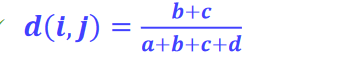
b:对象i为 1、对象j为 0 的属性数量;
c:对象i为 0、对象j为 1 的属性数量;
- 同理,采用简单匹配系数评价两个对象之间的相似度:

5.3 不对称二元变量
通常我们会把出现几率小的结果编码为 1(比如 "患病""检测阳性" 这类罕见情况),而 "0" 代表常见情况(如 "健康""检测阴性")。此时,"两个都为 1(正匹配)" 比 "两个都为 0(负匹配)" 更有分析价值(因为 0 可能是 "无信息" 的常见情况)。
Jaccard 系数(衡量相似性)
J ( i , j ) = a a + b + c J(i,j) = \frac{a}{a + b + c} J(i,j)=a+b+ca
- a:两个对象都为 1的属性数量(正匹配,有意义的相似);
- b:对象i为 1、对象j为 0 的数量;
- c:对象i为 0、对象j为 1 的数量;
含义:有意义的相似属性占总 "有差异和有意义" 属性的比例,结果越接近 1,相似性越高
Jaccard 距离(衡量相异性)
d J ( i , j ) = 1 − J ( i , j ) = b + c a + b + c d_J(i,j) = 1 - J(i,j) = \frac{b + c}{a + b + c} dJ(i,j)=1−J(i,j)=a+b+cb+c
含义:有差异的属性占总 "有差异 / 有意义" 属性的比例,结果越接近 1,相异性越高。
Eg.

- gender是一个对称的二元变量,不考虑
- 其他的都是非对称的二元变量
- 将Y和P编码位1,N编码为0,根据Jaccard系数计算得
将Fever、Cough、Test-1、Test-2、Test-3、Test-4这 6 个特征进行编码,得到每个个体的特征向量:
- Jack:([1, 0, 1, 0, 0, 0])
- Mary:([1, 0, 1, 0, 1, 0])
- Jim:([1, 1, 0, 0, 0, 0])
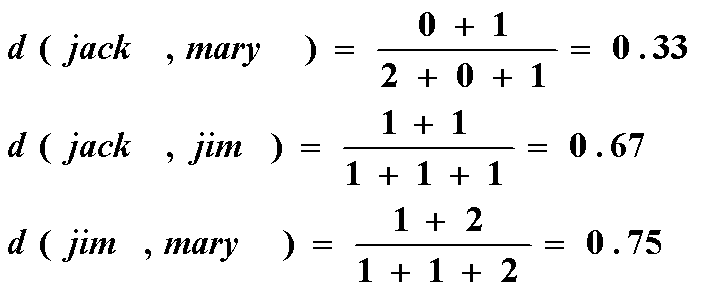
6.标称变量(属性)相异性
Nominal (Categorical) attributes:标称变量是对二元变量的推广,他可以具有多于两个的状态,比如变量map_color可以有 red, yellow, blue, green四种状态。
两种计算相异度的方法:
6.1 简单匹配方法
简单匹配方法(Simple Matching Method, SMM)
相异度d(i,j)
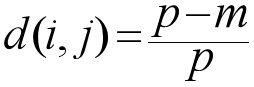
- m:两个对象在所有变量上 "状态相同" 的个数(匹配数)。
- p:标称变量的总个数(如同时考虑 map_color、size 两个标称变量,p=2)。
计算步骤
- 确定要比较的两个对象(如对象 A、对象 B)。
- 逐个变量对比状态:若 A 和 B 的状态一致(如 A 的 map_color=red,B 的 map_color=red),则计入m。
- 代入公式,用 "总变量数 - 匹配数" 除以 "总变量数",得到相异度(取值 0~1,越接近 0 越相似)。
6.2 使用二元变量编码
把 1 个多状态标称变量,拆成 "状态数" 个二元变量(非对称编码),再用二元变量相异度公式计算。
- 编码规则:对每个状态创建 1 个二元变量,对象 "拥有该状态" 则记 1,"不拥有" 则记 0(默认状态可设为 0,特殊状态设为 1)。
- 如 map_color(red/yellow/blue/green)拆成 4 个二元变量:red (0/1)、yellow (0/1)、blue (0/1)、green (0/1)。
d J ( i , j ) = 1 − J ( i , j ) = b + c a + b + c d_J(i,j) = 1 - J(i,j) = \frac{b + c}{a + b + c} dJ(i,j)=1−J(i,j)=a+b+cb+c
Eg.

-
画出相异度矩阵
- 若两个对象标称变量状态相同,则相异度为0
- 若两个对象标称变量状态不同,则相异度为1
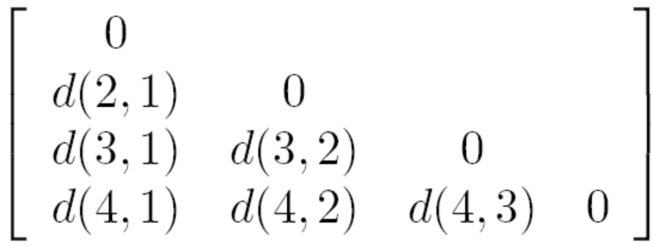
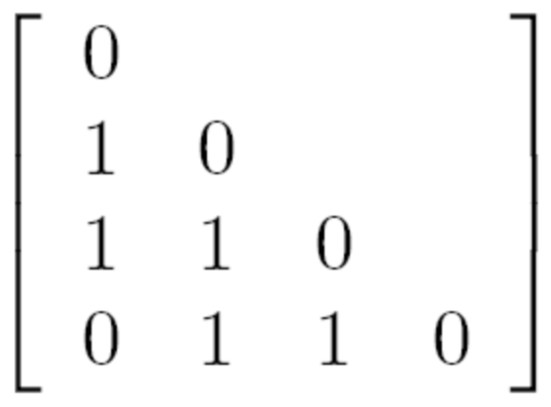
7.序列型变量的相异性
Ordinal Variables序数型变量,一个序列型变量既可以是离散的,也可以是连续的
如"好评、中评、差评"是有序离散的
相异性计算步骤:
-
给序数型变量 "赋值排序"
序数型变量有明确的顺序(如 "差评 < 中评 < 好评"),我们先给每个类别分配一个排序值:
- 假设 "差评" 排第 1,记为(r=1);
- "中评" 排第 2,记为(r=2);
- "好评" 排第 3,记为(r=3)。
-
将排序值 "规格化到 [0,1]"
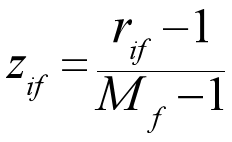
其中M是类别总数(这里(M=3))。
计算每个类别的规格化值:

- 用数值型的相异性公式计算
规格化后,序数型变量就变成了 [0,1] 之间的数值(类似连续数值型变量),这时可以直接用数值型属性的相异性度量(比如 "绝对差""欧氏距离" 等)来计算差异。

8.簇间的距离度量标准
8.1 簇间的距离度量标准
用于簇Ci和簇Cj之间的距离度量标准是
- 最小距离:找两个簇里离得最近的两个个体的距离。
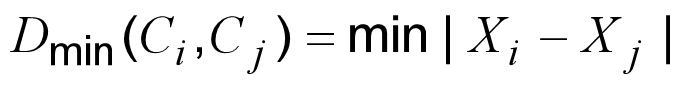
其中Xi∈Ci和Xj∈Cj
比如簇 A 有小明(身高 170)、小李(175),簇 B 有小王(172)、小张(180)→ 小明(170)和小王(172)离得最近,所以 Dmin=2。
- 最大距离:找两个簇里离得最远的两个个体的距离。
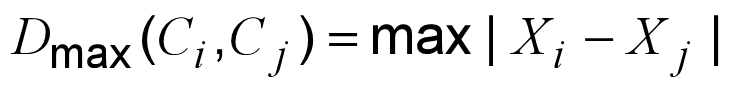
其中Xi∈Ci和Xj∈Cj
小李(175)和小张(180)离得最远,所以 Dmax=5。
- 中间距离:两个簇的 **"中心(质心)" 之间的距离 **
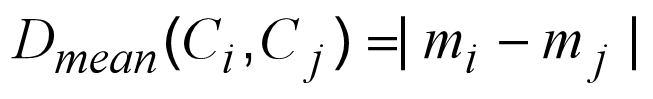
其中mi和mj是Ci和Cj的质心
簇 A 的质心是(170+175)/2=172.5,簇 B 的质心是(172+180)/2=176 → 中间距离 =|172.5-176|=3.5。
- 平均距离:把两个簇里所有个体之间的距离都算一遍,再求平均。
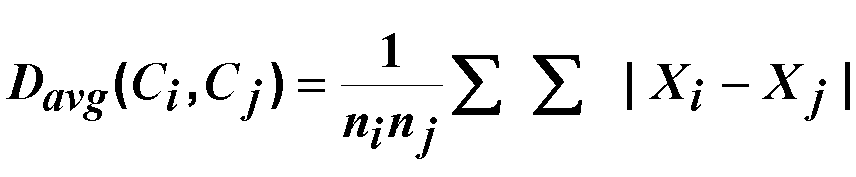
其中Xi∈Ci和Xj∈Cj,且ni和nj是类Ci和Cj间的样本数。
簇 A 和簇 B 的个体对有(小明 - 小王、小明 - 小张、小李 - 小王、小李 - 小张),距离分别是 2、10、3、5 → 平均距离 =(2+10+3+5)/(2×2)=5。
8.2 聚类准则函数
"误差平方和准则(Je)" 是判断聚类好不好的标准,核心逻辑是 "簇内越紧凑,聚类越好"。
误差平方和准则(sum-of-squared-error criterion):
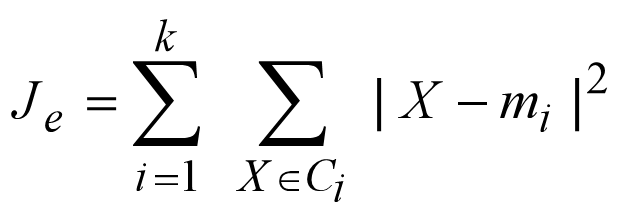
- 其中X∈Ci,mi是Ci的质心
- Je即所有样本的平方误差和。
它的计算是:把每个样本到自己簇中心的 "距离的平方" 加起来,总和越小,说明簇内越紧凑。
比如还是上面的簇 A(小明 170、小李 175,中心 172.5)和簇 B(小王 172、小张 180,中心 176):
- 小明到中心的平方距离:(170-172.5)²=6.25
- 小李到中心的平方距离:(175-172.5)²=6.25
- 小王到中心的平方距离:(172-176)²=16
- 小张到中心的平方距离:(180-176)²=16
- 总误差平方和 Je=6.25+6.25+16+16=44.5
如果聚类结果让这个 Je 更小,就说明簇内更紧凑,聚类效果更好。
根本目标:使得生成的结果簇尽可能的紧凑和独立
9. 聚类挖掘
聚类挖掘是无监督学习中 "给数据分组" 的技术,这三类算法可以通俗理解为:
- 基于划分的算法:像给学生分小组,先定好要分几个组(比如 K-means),然后反复调整成员,直到组内尽可能相似。
- 层次算法:类似建家族树,要么从每个数据自己当一个簇开始,不断合并相似的(凝聚式);要么从所有数据当一个簇开始,不断拆分(分裂式),最终形成层次化的簇结构。
- 基于密度的方法:好比找 "扎堆儿" 的人群,只要数据点的密度够高,就把它们划成一个簇(比如 DBSCAN),能有效识别不规则形状的簇,还能过滤噪声点。
9.1 分层聚类
分层(Hierarchical)聚类是通过尝试"对给定数据集进行分层"的方式达到聚类的一种分析方法。
根据分层分解采用的分解策略,分层聚类法又可以分为凝聚 (Agglomerative)的分层聚类和分裂(Divisive)的分层聚类。
分层聚类的思想比较简单,但为其他聚类算法的提出奠定了基础。分层聚类的关键在于选择合并点或者分裂点。
- 聚合法:最初将每个数据点作为一个单独的聚类,然后迭代合并,直到最后的聚类中包含所有的数据点。它也被称为自下而上的方法。
- 分裂聚类:遵循自上而下的流程,从一个拥有所有数据点的单一聚类开始,迭代地将该聚类分割成更小的聚类,直到每个聚类包含一个数据点。
下图展示的便是聚合法。
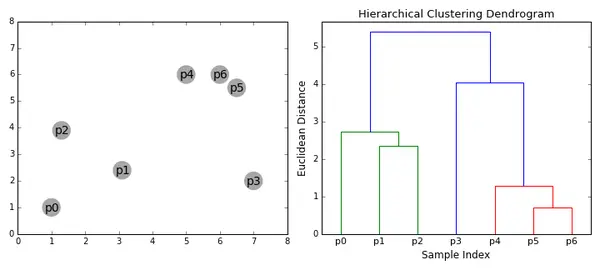
算法结束后不会直接给固定数量的簇,而是输出一个树状图。你想分几类,就在树的对应层级 "切一刀"
9.2 K-means聚类
属于基于划分的算法
K-means聚类是一种典型的基于聚类的聚类算法,它使用距离作为相似性的评价指标,即认为两个对象离得越近,其相似度就越高
K-means目的:寻找固定数目的簇,每个簇由距离靠近的对象组成

k-means 聚类中的 k 的含义是"该算法第一步是随机地选取任意 k 个对象作为初始聚类的中心"。
在 k-means 聚类中,k 个初始聚类中心点的选取对聚类结果的影响较大。
工作流程:
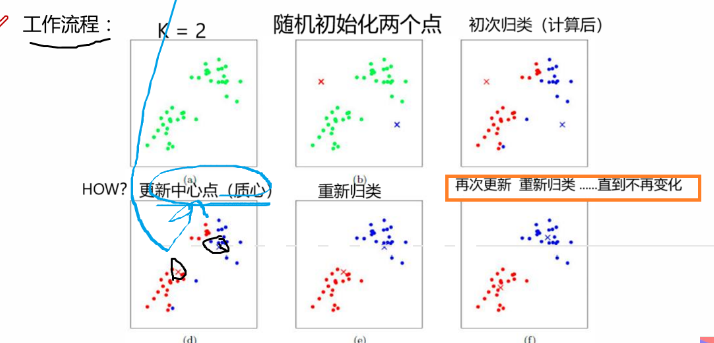
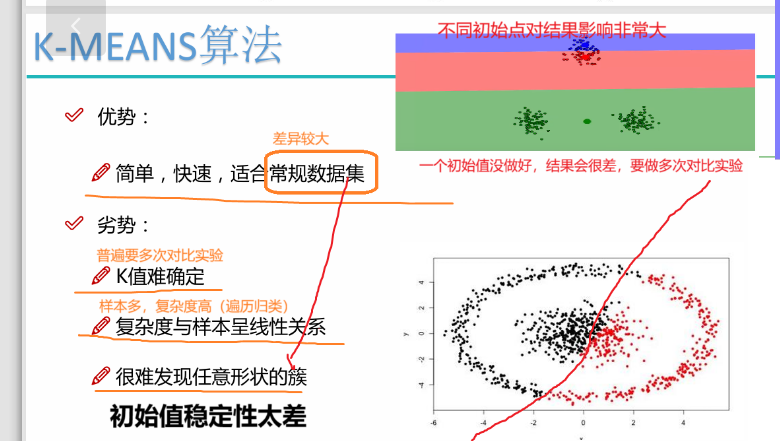
演示gif
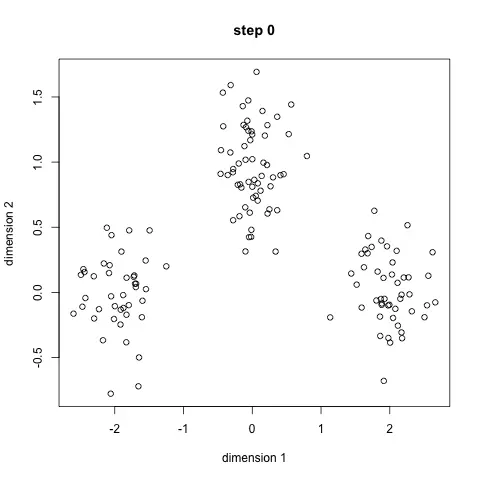
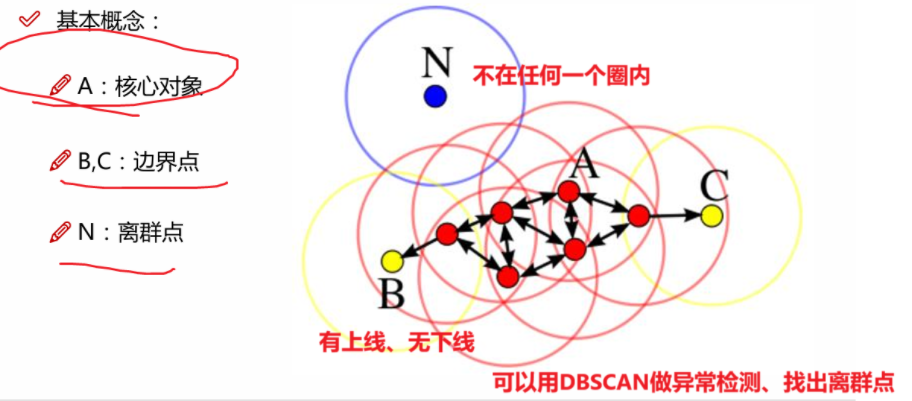
9.3 DBSCAN聚类
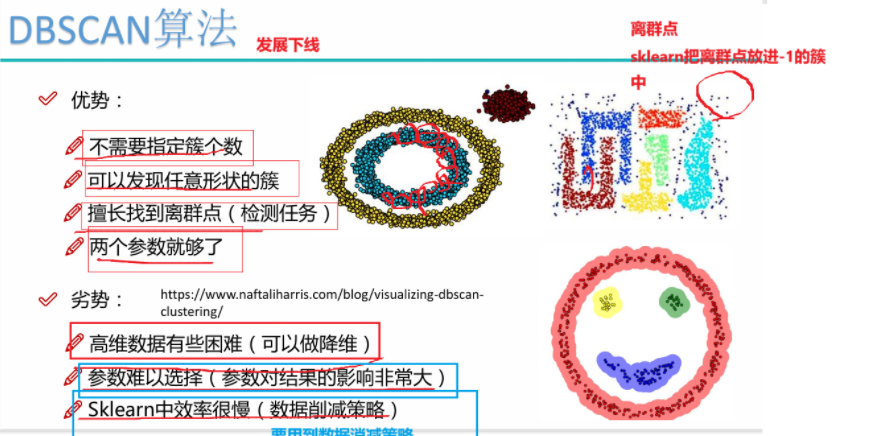
DBSCAN聚类首先是属于基于密度的聚类算法
采用密度作为划分簇的依据,即具有足够密度的区域将被划分为一簇,并可以在有噪声的空间数据中发现任意形状的簇。
DBSCAN 算法的目的是识别空间中具有足够密度的区域并将其标记为簇,并将无法密度可达的点标记为噪声。
密度由半径 eps 和最小样本数 MinPts 决定,簇定义为密度相连的点的最大集合。
在 DBSCAN 聚类中,半径 eps 和最小样本数 MinPts 的选取对聚类结果有较大影响,直接影响了聚类结果