分类问题当作回归问题分析
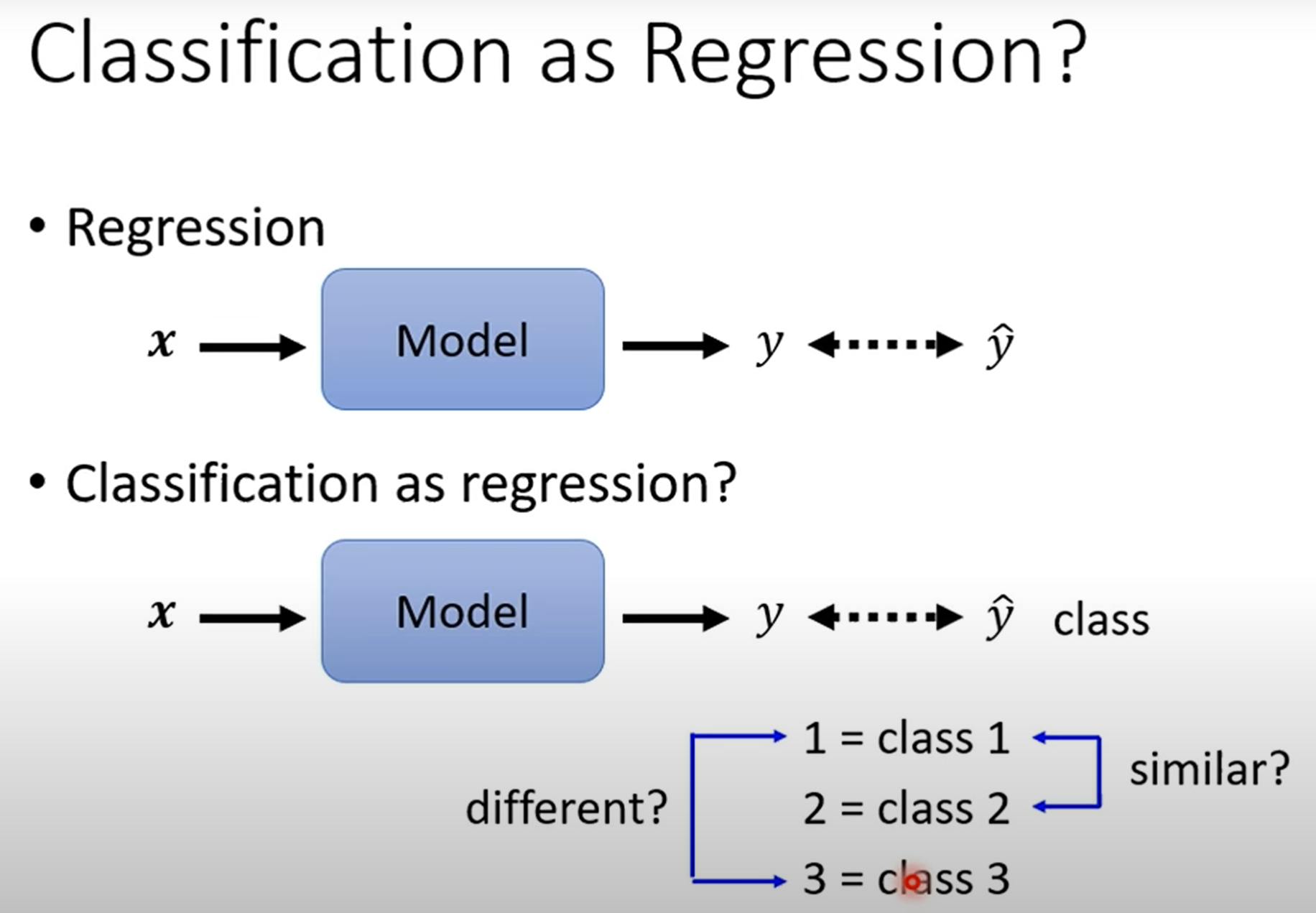
回归输出的是一个数值,而分类的目的是将输入进行归类。
一种简单的方法是将类别视为数值标签进行回归,但如果类别之间没有内在的数值关系,这种方法可能会产生问题。
一个常见的误区是直接用回归的方法来处理分类问题。比如,给"猫"赋予标签1,"狗"赋予标签2,"猪"赋予标签3,然后用一个回归模型去预测这个数值。
这样做有什么问题呢?
-
隐含的顺序关系 :这样做会给模型一个错误的暗示,即这些类别之间存在某种数学关系(例如,
狗是猫和猪的平均值?猪比狗更"大"?)。这在大多数分类场景下是不成立的。 -
多分类的局限:如果类别之间没有明确的顺序,这种方法很难扩展到多分类问题。
正确地表示分类目标: One-Hot 编码
-
概念:One-Hot 编码是一种将类别变量转换为机器学习算法易于处理的形式的方法。它将每个类别表示为一个向量,向量的长度等于总类别数,其中只有一个元素是1(表示当前类别),其余所有元素都是0。
-
举例:
-
类别1:
[1, 0, 0] -
类别2:
[0, 1, 0] -
类别3:
[0, 0, 1]
-
这样做的好处是,类别之间是相互独立的,模型不会错误地学习到它们之间不存在的数值关系。
修改输出(一个数值变成三组数组)
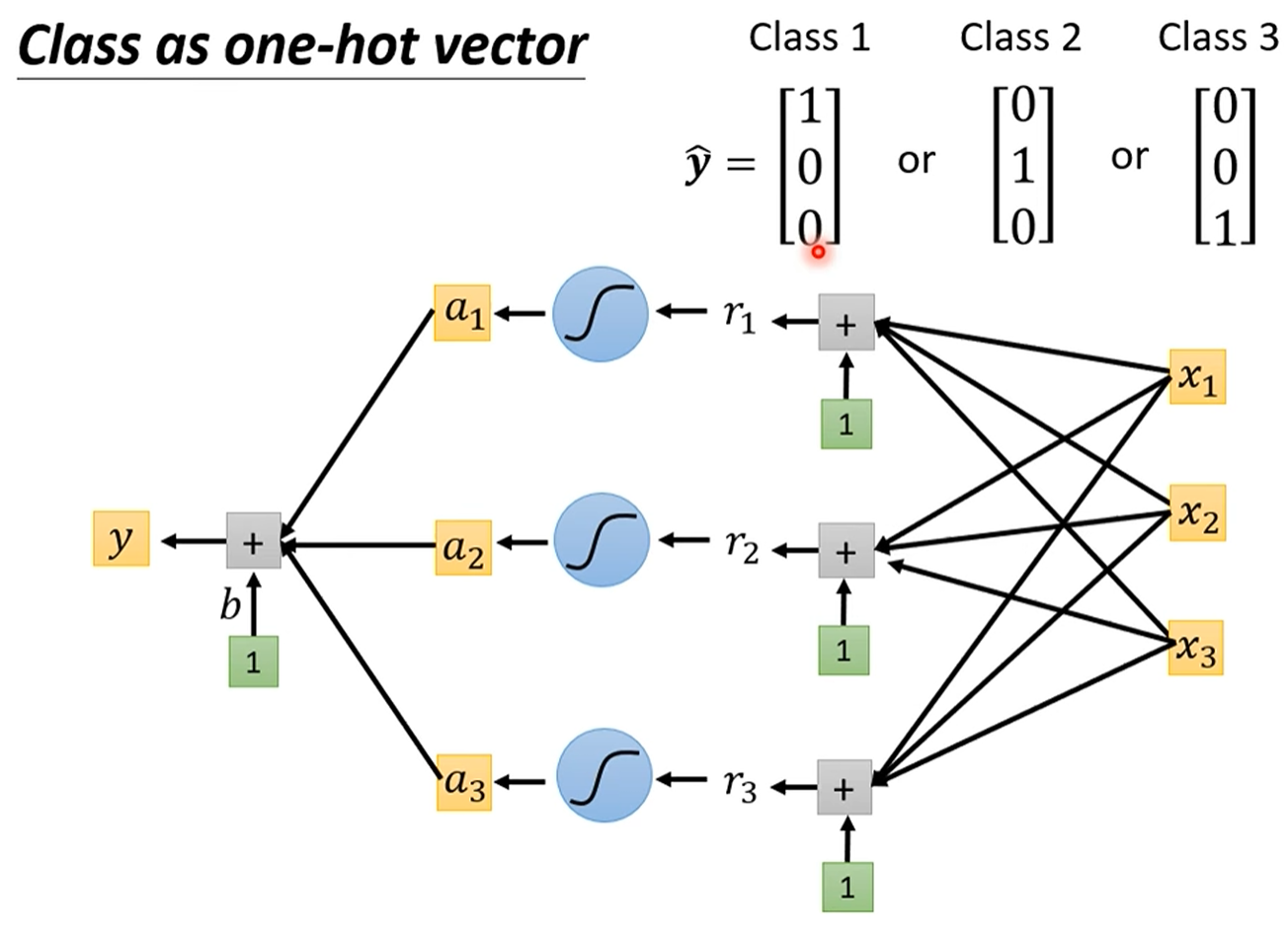
实际上在用深度学习解决分类问题的时候就是修改了神经网络的结构,把单一输出,变成一个向量输出,概率输出,从而达到了分类的效果
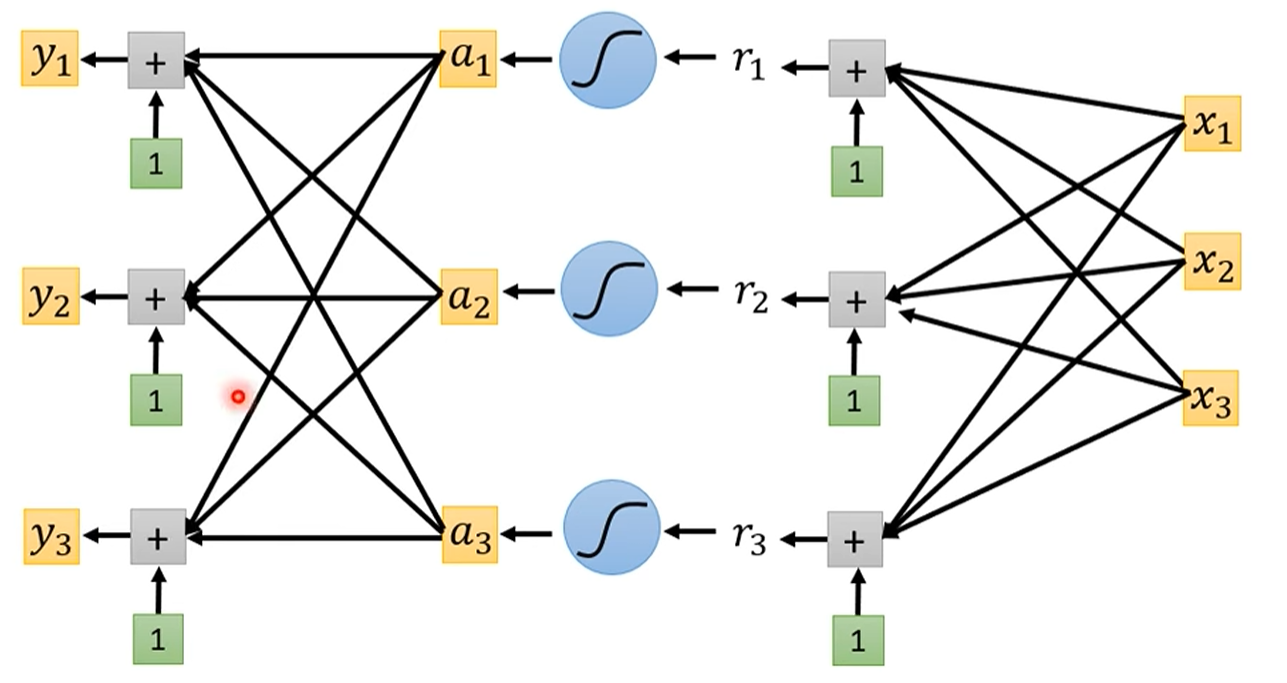
分类神经网络的输出:当使用 one-hot 编码作为目标时,神经网络需要输出多个值(例如,三个类别对应三个输出)。这可以通过复制输出层并应用不同的权重和偏置来实现
Softmax函数:
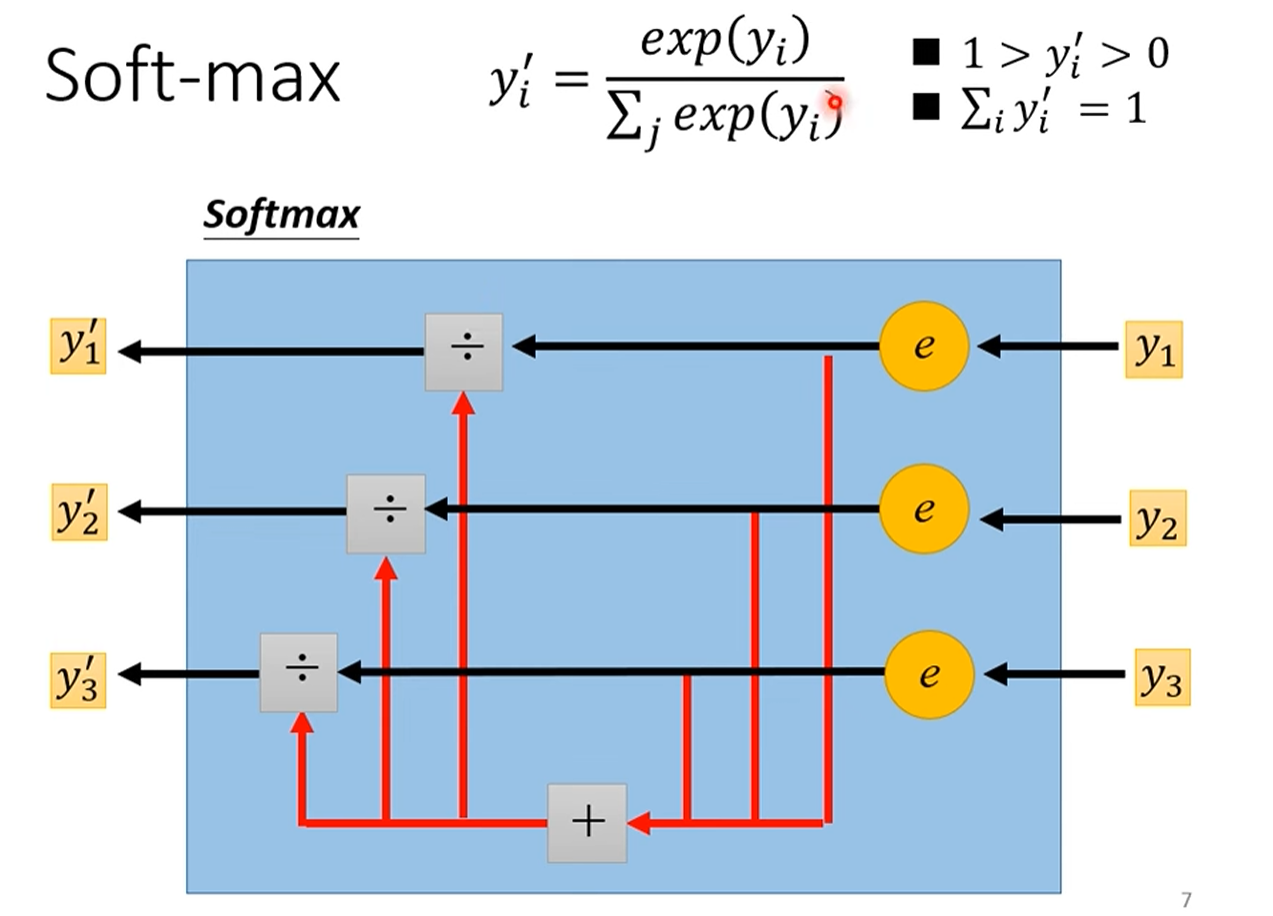
yiy_iyi输入叫logit
模型的输出层设计与 Softmax
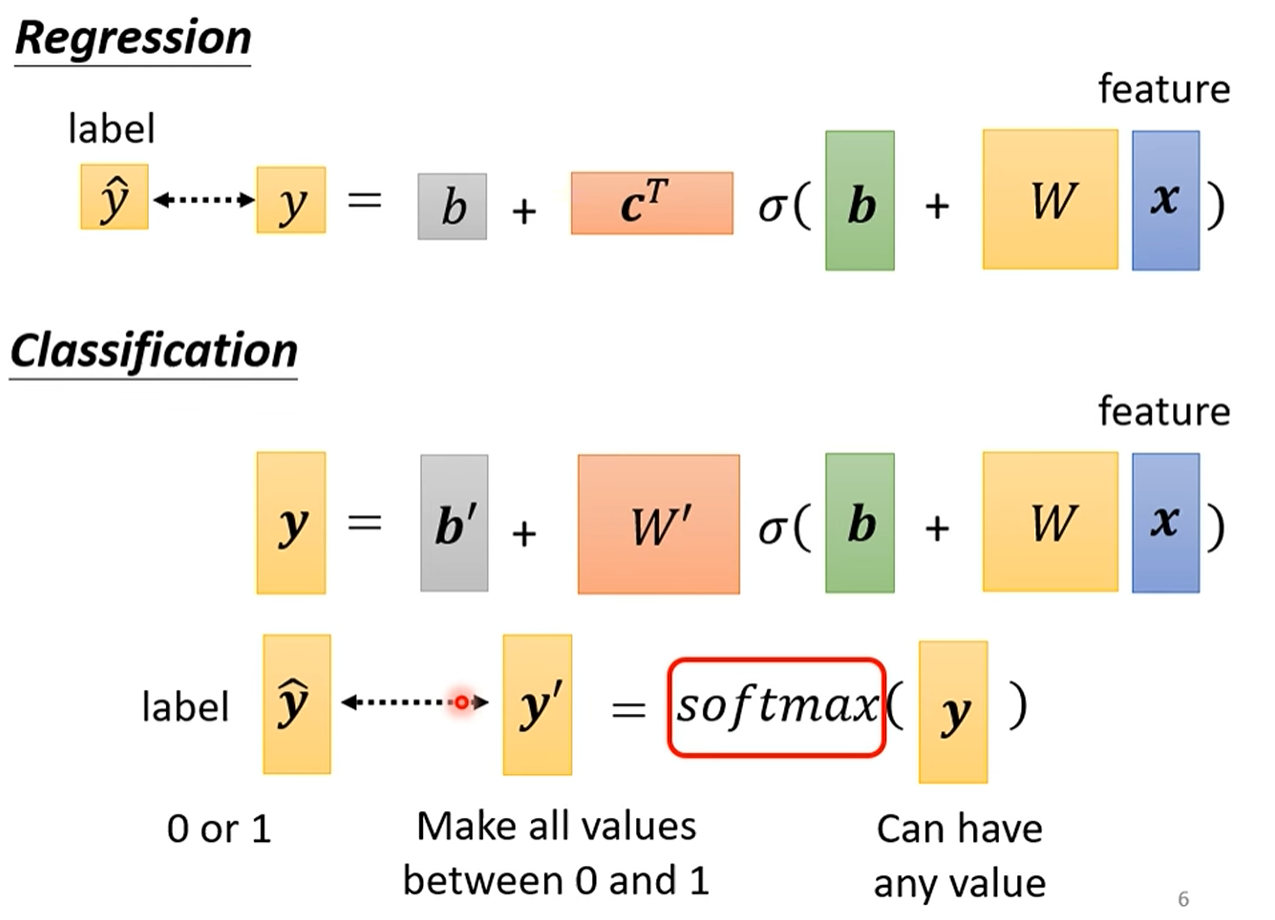
当我们的目标(Label)变成了 One-Hot 向量后,模型的输出(Output)也需要与之对应。
-
输出层设计:对于一个三分类问题,模型的输出层需要有3个神经元,分别对应三个类别的预测值。
-
问题 :这3个输出值可能是任意的实数,比如
[3.1, 1.9, 0.2]。我们如何将它转换成类似[0.7, 0.2, 0.1]这样,每个值都在0到1之间,且总和为1的"概率"形式呢? -
解决方案:Softmax 函数 Softmax 函数可以看作是一个"归一化"工具,它能将一组任意实数转换成一个概率分布。它的作用是:
-
放大差距:通过指数运算,将大的值变得更大,小的值变得更小。
-
归一化:将所有输出值缩放到0到1之间,并且它们的总和为1。
-
经过 Softmax 处理后,模型的输出 y' 就变成了一个可以和 One-Hot 标签 y 直接比较的概率向量了。
分类常用损失函数
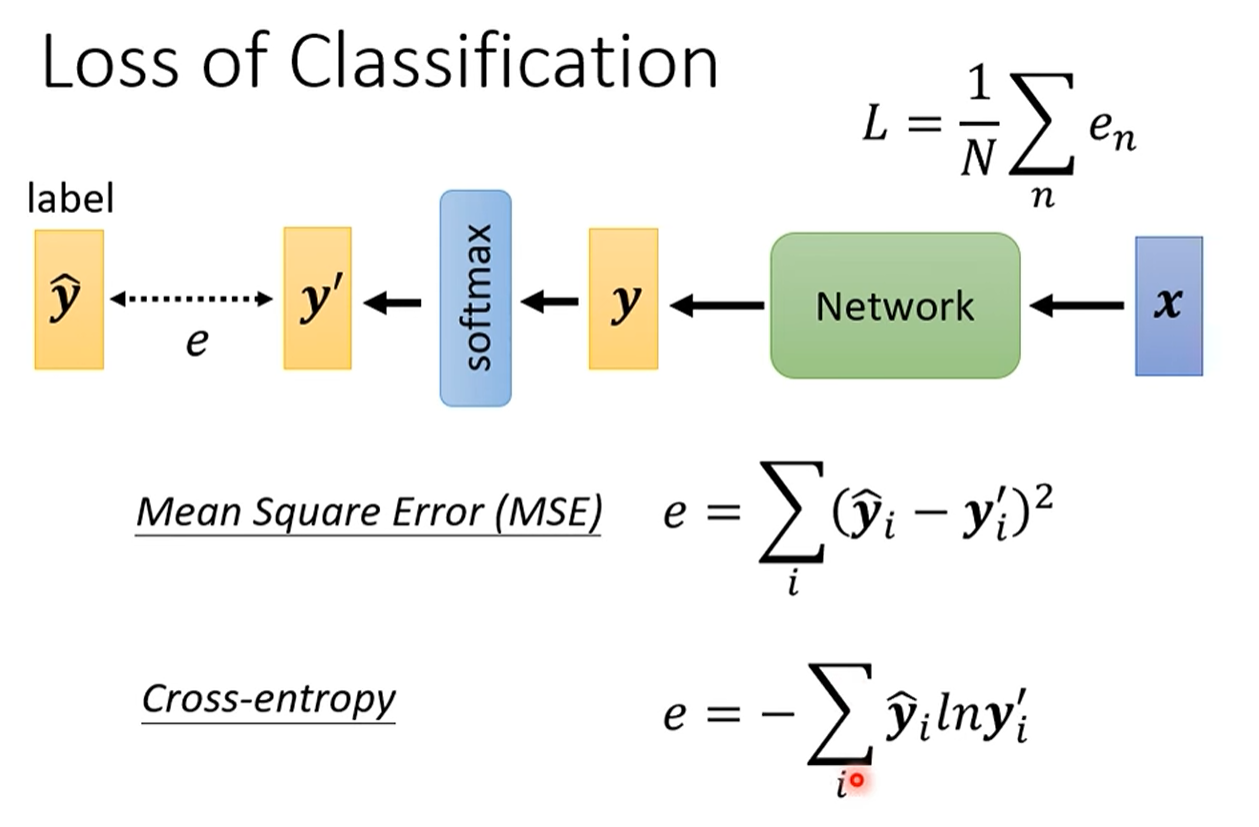
最小化交叉熵,从信息论的角度来看,等同于最大化对数似然(Maximizing Log-Likelihood),即让模型预测出真实标签的概率尽可能大。
数学角度分析
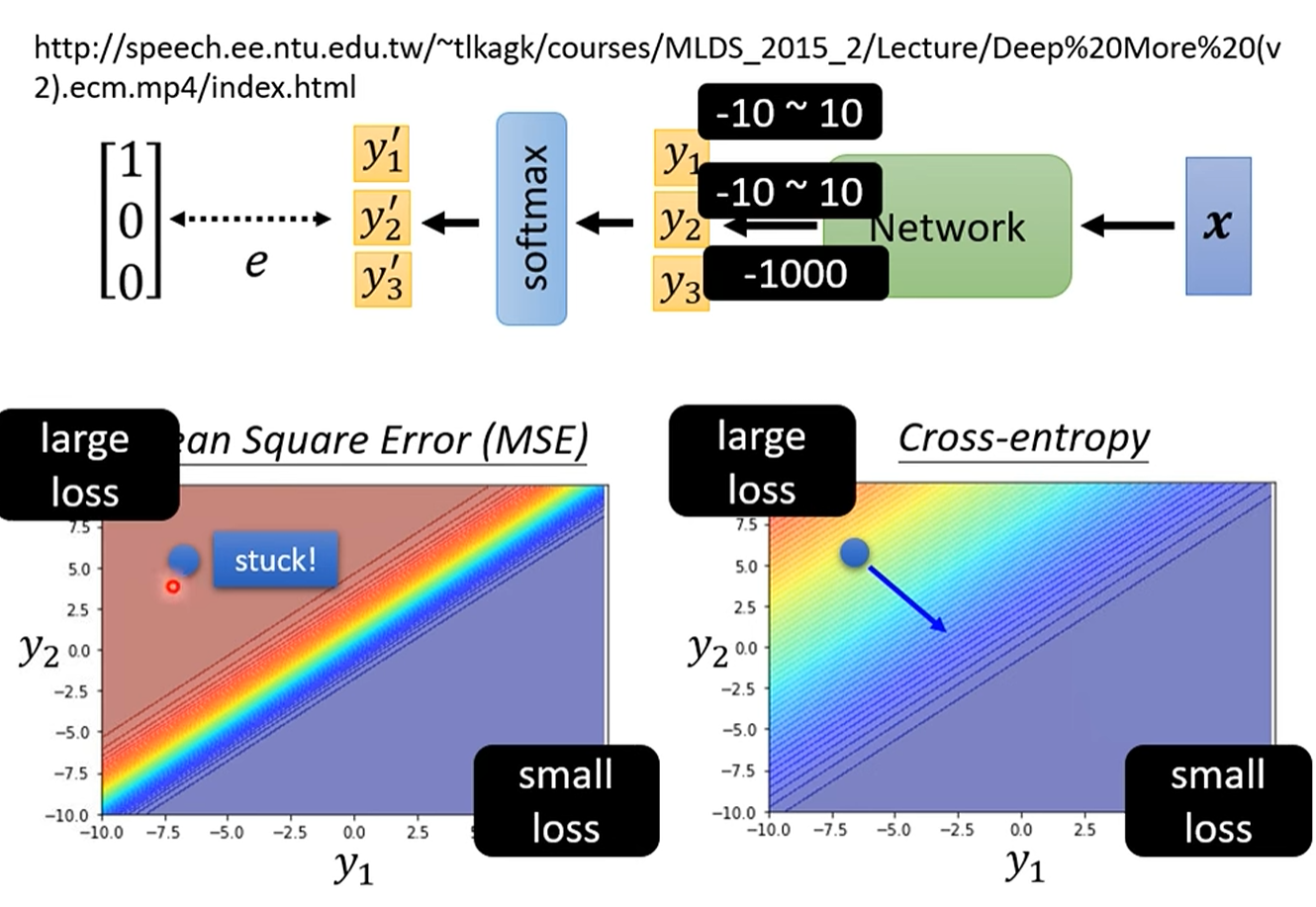
均方误差 (MSE) vs. 交叉熵 (Cross-Entropy)
-
均方误差 (MSE)
-
原理 :直接计算模型输出概率
y'和真实标签y之间每个元素的差值的平方和。 -
问题 :在分类问题中,MSE 的一个致命缺点是,当模型的预测非常糟糕时(例如,对于正确类别预测的概率接近0),它的梯度(也就是给模型的"纠错信号")会变得非常小,几乎消失。这被称为 梯度消失。
-
-
交叉熵 (Cross-Entropy)
-
原理 :交叉熵源自信息论,它衡量的是两个概率分布之间的"差异"或"距离"。在机器学习中,它衡量的是模型预测的概率分布
y'与真实的标签分布y之间的差异。 -
优势 :交叉熵的一个巨大优势是,当模型的预测错得越离谱,它计算出的损失值就越大,产生的梯度也越大。
-