Batching and Matching for Food Delivery in Dynamic Road Networks论文学习
这篇论文提出了FOODMATCH方法。一种基于最小权二分图匹配的高效实时送餐派单算法。将订单-车辆分配转化为带权二分图匹配,并以最佳优先搜索构建精简子图,实现多项式时间近似;把订单批次化建模为图聚类,并利用角距离预测车辆动态位置,显著降低平均送达时间。大规模真实数据验证其优于基线策略且满足在线需求。
建模
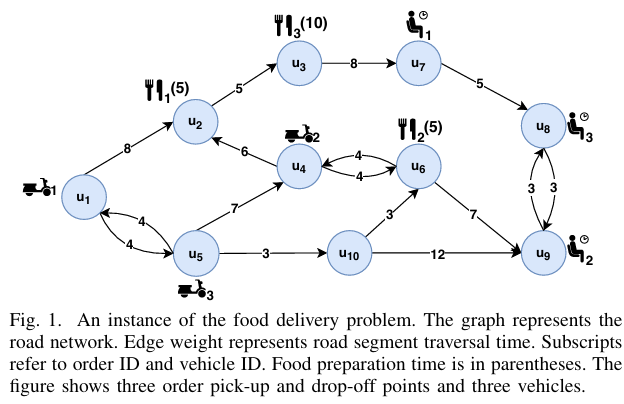
• 路网:时变有向图 G=(V,E,τ(t)),τ(t) 为实时通行时间。
• 订单:o=(oʳ,oᶜ,oᵗ,oᶦ,oᵖ),分别表示取餐点、送达点、请求时间、商品数、备餐时长。
• 车辆:实时位置 loc(v,t),容量 MAXO 单/MAXI 件,按最快路径执行。
关键度量
• EDT(o,v)=max{time(A)+firstMile(o,v), oᵖ}+lastMile(o,v)
• SDT(o)=oᵖ+SP(oʳ,oᶜ) 为理论下界
• XDT(o)=EDT−SDT 为额外延迟
问题定义(FDP)
在线输入订单流 O 与车辆流 V,求指派 A 最小化Σo XDT(o,A)·(1−ρ(o))+ρ(o)·Φ,
其中 ρ(o)=1 表示拒单,Φ 为高额惩罚。
复杂度
单车辆、零备餐特例等价于 SS-OL-DARP-F;据 Krumke [17] 可知在线 FDP 不仅 NP-hard,且对任意 ε>0 无 n^{1−ε} 近似。
问题不可近似,必须依赖可扩展启发式算法(如后文 FOODMATCH)。
机制
• 以长度 Δ 的累积窗口收集未派单订单 O(τ) 与可用车辆 V(τ)。
• 每次迭代选 (o*,v*) = argmin mCost(o,v),其中mCost(o,v)=Cost(v∪{o})−Cost(v),Cost(v)=Σo∈v XDT(o,v)。
• 直至无可行指派或容量用尽为止。
每轮需枚举 ≤2MAXO 位置的全排列并求最短路径,总时间 O(MAXO (MAXO!) q(mn+n^2)),其中 q 为单源最短路耗时。
Δ 的权衡
• 增大 Δ:批量大→潜在成本降低,但待派单延迟↑、每窗口计算量↑。
• 减小 Δ:延迟↓,计算频繁,车辆位置查询次数↑。无理论保证,需实验调优。
FOODGRAPH 最小权匹配
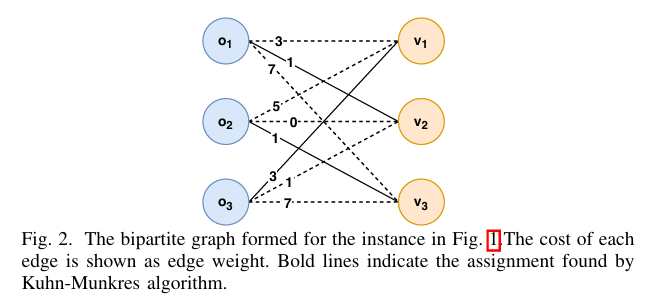
• 构造二分图:U₁=订单,U₂=车辆,边权 w(o,v)=mCost(o,v)。
• Kuhn-Munkres 求最小权完美匹配,实例比 Greedy 优 1 单位。
• 复杂度 O(nm·MAXO·MAXO!·q + k²k'),n=|O|, m=|V|, k=min(n,m)。
• 缺陷:无批处理;n>m 时大量拒单;权重在求解期间可能过时。
批处理(Batching)
思想
将可同车配送的多单合并为"批次节点",再参与二分图匹配。
方法
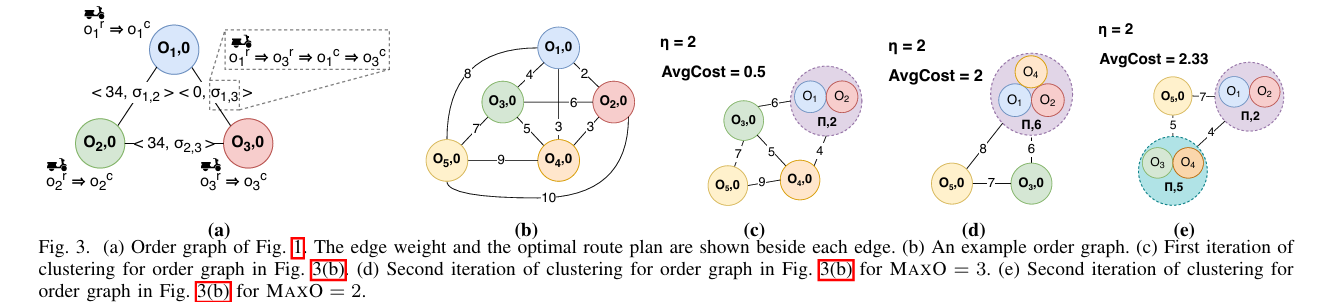
• 构建 Order Graph G_O:节点=当前批次,边当且仅当合并后容量不超 MAXO/MAXI;边权
w_ij = Cost(v, i∪j) -- [Cost(v_i,i)+Cost(v_j,j)]。
• 迭代聚类:每轮合并最小 w_ij 的两批次,更新边权;当 AvgCost(G_O) 超过阈值 Φ 时停止。
• AvgCost 随迭代单调不降→算法收敛。
建图 O(n²q);共 ≤n--1 轮,每轮 O(n log n + n·MAXO·MAXO!·q);总时间Õ(n²·MAXO·MAXO!·q)。
动机
• 实证发现:把"所有车辆"和"所有订单"按车辆到餐厅的实际路网距离排序,95 % 的车最终被分到的那个订单,都排在自己"最近 10 % 的候选订单"里→可仅保留最近 k 批订单的边。
• 挑战:如何在不逐一算距的情况下找出这些"最近批次"。
方法:Best-First 稀疏化
• 对每辆车 v:
-- 仅考虑各批次的首取餐节点集合 V⊂V。
-- 由 loc(v,t) 启动最佳优先搜索(BFS+优先队列),按最短路径长度递增访问节点。
-- 每遇节点 u,即连边 v→所有以 u 为首节点的批次,权重用批级 mCost(·)。
-- 一旦 v 的度数达 k 或队列为空,停止搜索,其余批次以拒单惩罚 Φ 建边。
复杂度削减
• 完整图需 O(n·m·MAXO·MAXO!·q)。
• 稀疏化后每辆车仅连 ≤k 条边,整体降为 O(m·(k log|V| + k·MAXO·MAXO!·q))。
引理
若某批次与 v 的真实边权 <Φ,则该批次必被算法发现并位于前 k 最近。
动态问题
FOODGRAPH 构建期间车辆持续移动,原"最近批次"可能在完成时已非最近,导致指派失效。
解决思路
Angular Distance
• 用方位角(bearing)量化车辆前进方向与候选节点方向之间的夹角 θ∈[0,π];
• 定义角距 adist = (1--cos θ)/2 ∈[0,1],0 表示同向,1 表示反向。
• 边权改为时间距离与角距的加权:
w(e,t)= (1--λ)·adist + λ·τ(e,t)/τ_max
重排(Reshuffling)
利用餐厅备餐缓冲:凡尚未取餐的订单与车辆都可重新加入下一窗口的匹配池,及时修正过时指派。
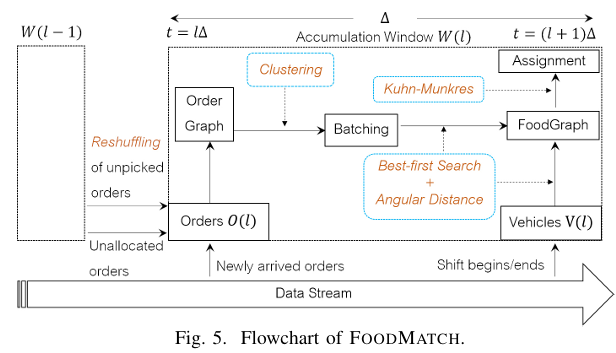
整体流程(图 5)
累积窗口收集未派单 + 可重排订单 → 2. 批处理 → 3. 用角距+best-first 构建稀疏 FOODGRAPH → 4. Kuhn-Munkres 最小权匹配 → 输出指派。
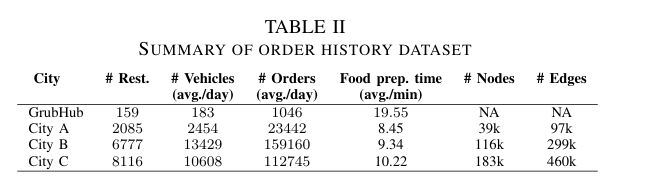
数据集
• GrubHub(公开)+ Swiggy 三城 6 天全量订单(City A/B/C,B 最繁忙)。
• 路网来自 OSM,边权/备餐时间按 24 时段实时均值建模;GPS 轨迹已 map-matched。
实验结果
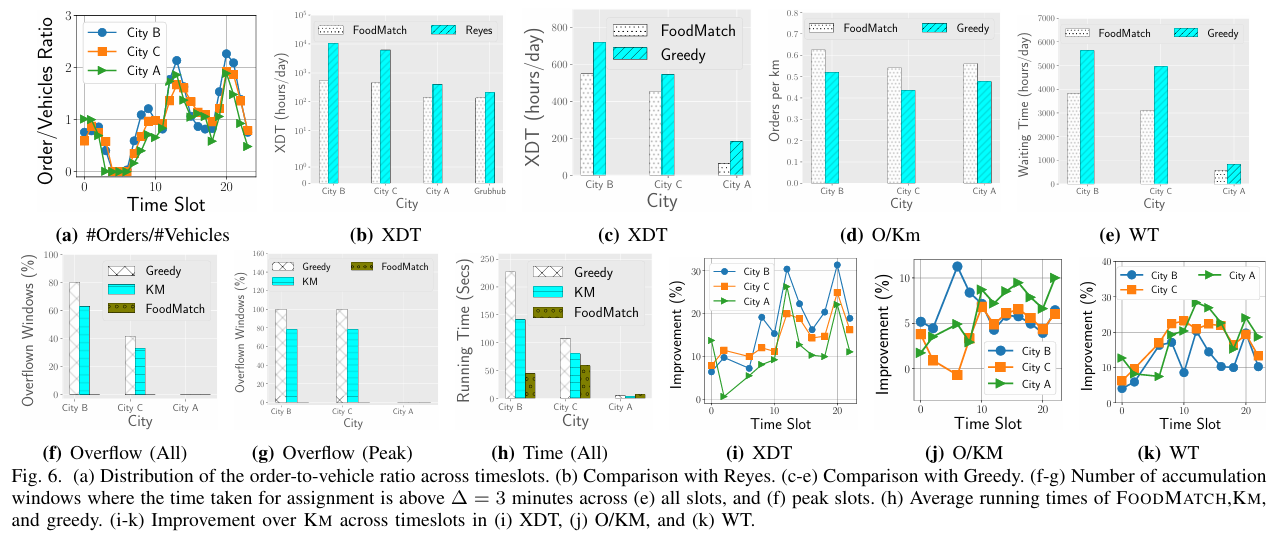
与 Reyes 比较
Reyes 仅用 Haversine 距离、同店批单 → 完全忽略道路拓扑;在 City B/C 日均额外延误(XDT)≈ FOODMATCH 的 10 倍。
在 GrubHub 公开集上差距缩小到 1.4 倍,原因:① FOODMATCH 无路网可用;② 订单量低,批处理/重排收益有限。
订单--车辆比越高的场景,Reyes 性能衰减越显著(午餐/晚餐高峰 XDT 峰值为 FOODMATCH 的 11--12 倍)。
与 Greedy 比较
全局目标优化带来 30 % 的 XDT 削减(City B 绝对值从 18.7 min → 13.1 min)。
等待时间 WT:
• City B 每日减少 2043 人·时;
• City C 每日减少 1987 人·时。
运营效率 Orders/Km 提升 20 %(City B 从 0.83 → 1.00 order/km)。
高并发时段(12--14 点、19--21 点)Greedy XDT 峰值比 FOODMATCH 高 38--42 %。
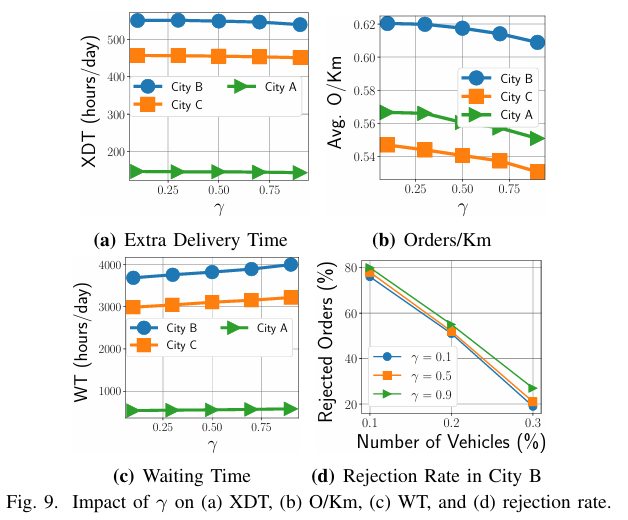
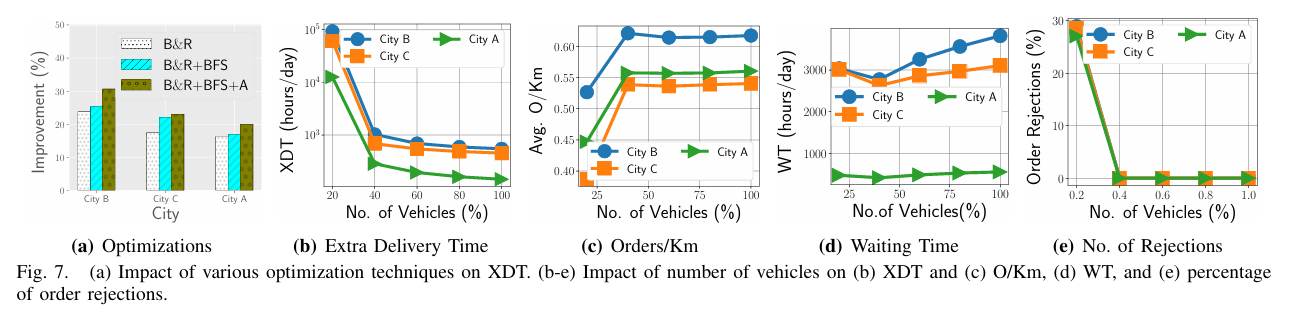
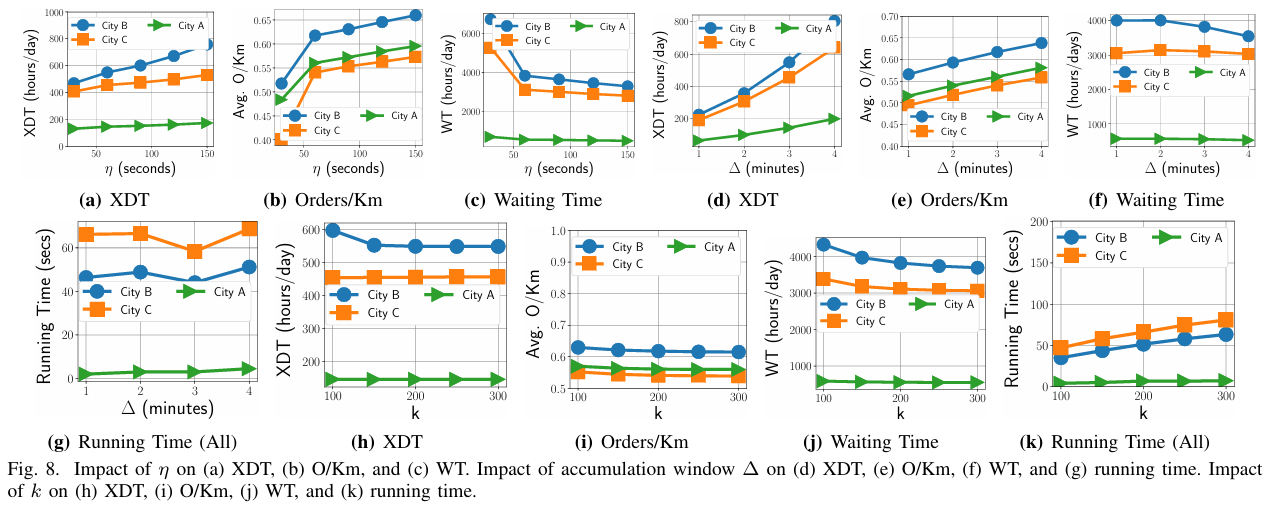
参数重要性
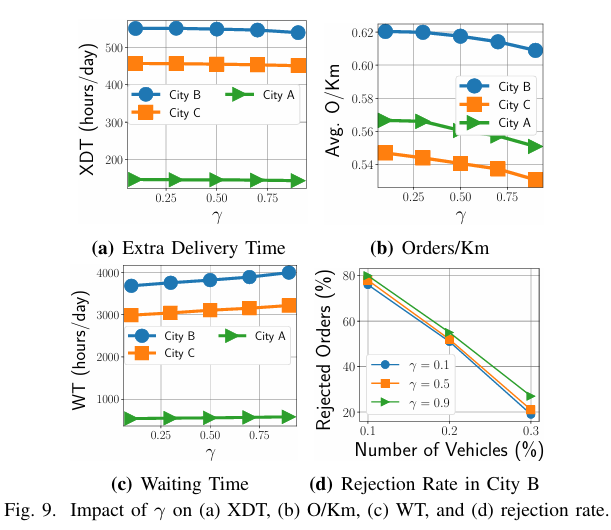
结论
FOODMATCH 在大规模真实数据上验证:相较 Reyes 将额外配送时间压缩一个数量级,比 Greedy 再降 30 %;车辆空驶减少、人时等待降低 40 %,且在百万级订单城市实时可部署,为外卖行业提供了可落地的全局优化框架与开源基准。