机器学习 K-Means聚类无监督学习

[K-Means 聚类：从原理到实践的完整指南](#K-Means 聚类：从原理到实践的完整指南)

[什么是 K-Means 聚类？](#什么是 K-Means 聚类？)

应用场景举例

[K-Means 算法的核心原理](#K-Means 算法的核心原理)

[K-Means 算法的步骤详解](#K-Means 算法的步骤详解)

可视化理解

[K-Means 的优缺点分析](#K-Means 的优缺点分析)

优点

缺点

[如何选择合适的 K 值？](#如何选择合适的 K 值？)

[1. 肘部法（Elbow Method）](#1. 肘部法（Elbow Method）)

[2. 轮廓系数（Silhouette Score）](#2. 轮廓系数（Silhouette Score）)

[K-Means 的改进算法](#K-Means 的改进算法)

总结

一.K-Means 聚类：从原理到实践的完整指南

聚类分析是机器学习中一种重要的无监督学习方法，它能够将相似的数据点自动分组，发现数据中潜在的结构和模式。在众多聚类算法中，K-Means 因其简单、高效和广泛的适用性而成为最受欢迎的算法之一。本文将深入解析 K-Means 聚类算法的原理、实现步骤、优缺点及实际应用案例。

1.什么是 K-Means 聚类？

K-Means 是一种迭代式的聚类算法，其核心思想是将 n 个数据点划分为 k 个不同的簇（Cluster），使得每个簇内的数据点具有较高的相似度，而不同簇之间的数据点差异较大。

"K" 代表我们想要创建的簇的数量，"Means" 则指每个簇的中心点（质心），算法通过计算数据点与质心的距离来决定数据点的归属。

应用场景举例

K-Means 在实际生活中有着广泛应用：

客户分群：电商平台根据用户购买行为将客户分为不同群体，进行精准营销
文本聚类：将新闻文章按主题自动分类
图像分割：识别图像中不同的物体区域
异常检测：发现数据中的异常值或离群点
市场细分：根据消费者特征划分不同的市场群体

2.无监督学习与有监督学习的区别

有监督学习：需要X和Y数据，Y作为监督信号，模型通过Y优化预测结果（如分类、回归）。
无监督学习：仅使用X数据，无Y标签，通过数据内在结构进行聚类（如K-means）。

3.K-Means 算法的核心原理

K-Means 算法的工作流程基于以下关键概念：

簇（Cluster）：具有相似特征的数据点集合
质心（Centroid）：每个簇的中心点，是该簇内所有数据点的平均值
距离度量：通常使用欧氏距离衡量数据点与质心的相似度
目标函数：最小化所有数据点到其所属簇质心的距离之和（平方误差和）

4.K-Means 算法的步骤详解

K-Means 算法通过迭代方式逐步优化聚类结果，具体步骤如下：

确定 K 值：根据业务需求或数据特点，指定要创建的簇数量 K
初始化质心：随机选择 K 个数据点作为初始质心
分配数据点：计算每个数据点到 K 个质心的距离，将数据点分配到距离最近的质心所在的簇
更新质心：计算每个簇内所有数据点的平均值，作为新的质心
重复迭代：重复步骤 3 和步骤 4，直到质心不再显著变化或达到预设的最大迭代次数
输出结果：得到最终的 K 个簇及对应的质心

可视化理解

想象在二维平面上有一些散点，K-Means 的过程就像是：

先在平面上随机放 K 个 "种子" 点（初始质心）
每个点都选择离自己最近的种子点 "站队"
每个队伍计算出自己的 "中心位置"（新质心）
所有点根据新的中心位置重新选择队伍
重复以上过程，直到每个队伍的中心位置稳定下来

5.K-Means的评价指标(轮廓系数)

轮廓系数用于评估聚类效果，公式涉及两个关键指标：
- a_i：样本点与同簇其他点距离的平均值（簇内距离）。
- b_i：样本点到其他簇所有点距离的最小平均值（簇间距离）。
单个样本的轮廓系数计算公式为：
s_i = （b_i - a_i)\max(a_i, b_i)
整体轮廓系数为所有样本轮廓系数的平均值 ，取值范围为 [-1, 1]：
- 接近 1：聚类效果优秀。
- 接近 -1：聚类效果差（样本可能被误分到其他簇）。
- 接近 0：样本位于簇边界。

6.K-Means 的优缺点分析

优点

算法简单易懂，实现方便
计算效率高，对大数据集表现良好
聚类结果可解释性强
适用于高维数据

缺点

需要预先指定 K 值，而最佳 K 值往往不明确
对初始质心的选择敏感，可能导致不同的聚类结果
对噪声和异常值敏感
不太适合发现非凸形状的簇
当簇的大小差异较大时表现不佳

7.如何选择合适的 K 值？

选择合适的 K 值是 K-Means 聚类的关键挑战之一。以下是两种常用方法：

1. 肘部法（Elbow Method）

肘部法通过绘制 "K 值 - 误差平方和" 曲线来确定最佳 K 值：

计算不同 K 值（如 1 到 10）对应的聚类结果
计算每个 K 值下的误差平方和（SSE），即所有数据点到其簇质心的距离平方之和
绘制 K 值与 SSE 的关系曲线
曲线中 "肘部" 对应的 K 值即为最佳选择，此时 SSE 开始趋于平稳

2. 轮廓系数（Silhouette Score）

轮廓系数用于衡量聚类结果的质量：

取值范围为 [-1, 1]
接近 1 表示样本聚类合理
接近 0 表示样本可能位于两个簇的边界
接近 - 1 表示样本可能被分到错误的簇

选择轮廓系数最高的 K 值作为最佳聚类数量。

K-Means 的改进算法

由于基本 K-Means 存在一些局限性，研究者提出了多种改进算法：

K-Means++：改进了初始质心的选择方法，使质心尽可能远离，提高聚类效果
Mini-Batch K-Means：对大数据集更高效，使用部分样本计算质心
Bisecting K-Means：层次化聚类方法，通过不断二分簇来构建聚类结果
Kernel K-Means：利用核函数将数据映射到高维空间，能够处理非凸形状的簇

在 scikit-learn 中，KMeans类默认使用n_init='auto'参数，会根据数据情况自动选择合适的初始质心数量，实际上已经包含了 K-Means++ 的改进。

总结

K-Means 聚类是一种简单而强大的无监督学习算法，能够有效地发现数据中的自然分组。尽管它存在需要预先指定 K 值、对初始质心敏感等局限性，但通过合理选择参数和结合其他评估方法，K-Means 仍然是数据分析和挖掘中的重要工具。

在实际应用中，建议：

对数据进行标准化处理，消除量纲影响
结合多种方法确定最佳 K 值
多次运行算法，避免因初始质心选择不当导致的局部最优
可视化聚类结果，直观理解数据结构

二.案例实现（酒类数据聚类）

1.K-Means参数

源码如下

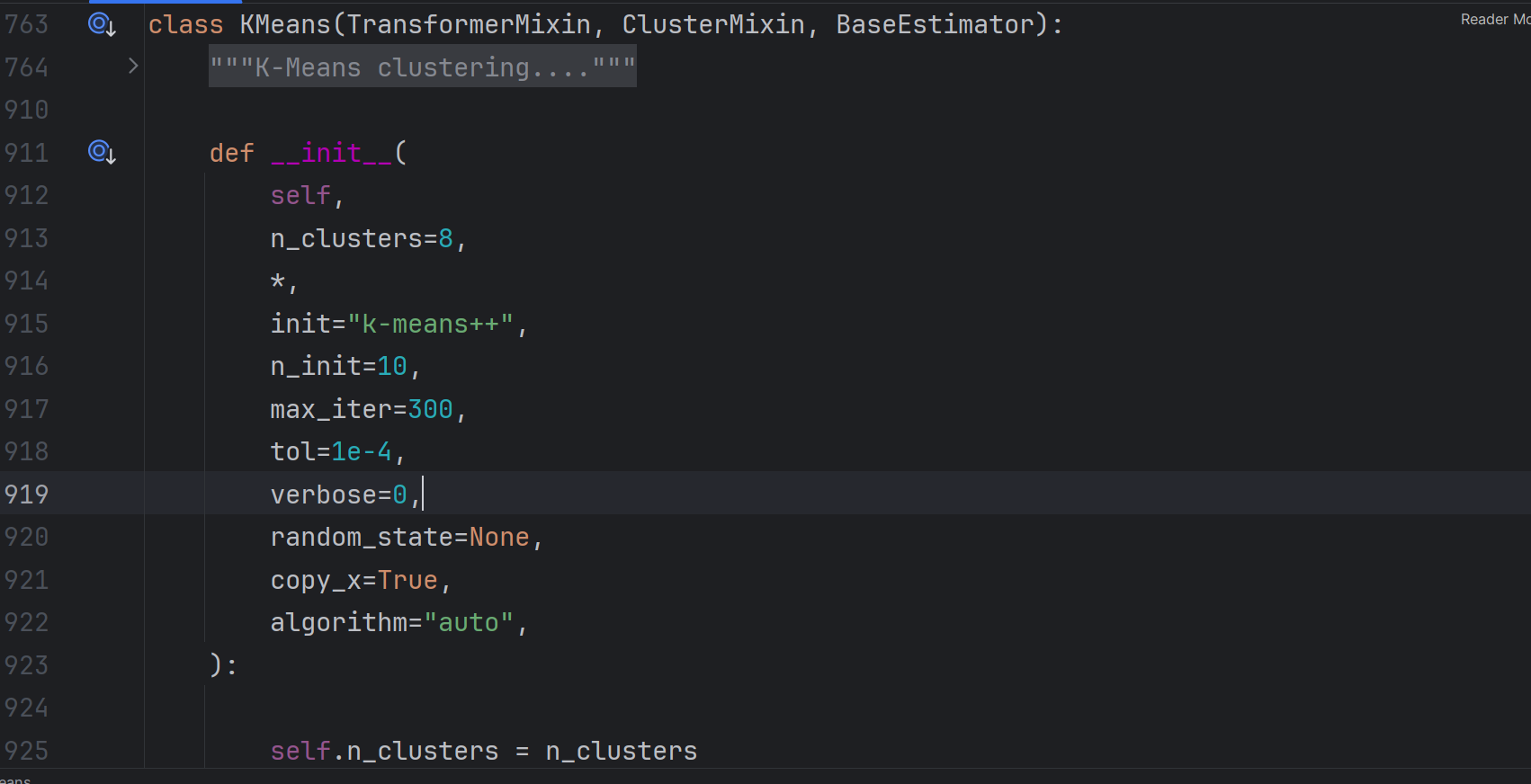
n_clusters：指定聚类中心数量（K值）。
init：初始化质心方法（默认 k-means++，优于随机初始化）。
n_init：初始化质心的次数（默认10次，避免因初始质心选择不佳影响结果）。
max_iter：单次K-Means算法的最大迭代次数（默认300）。

2.读取数据

数据特征：卡路里、氮浓度、酒精浓度、价格。data.txt部分内容如下：

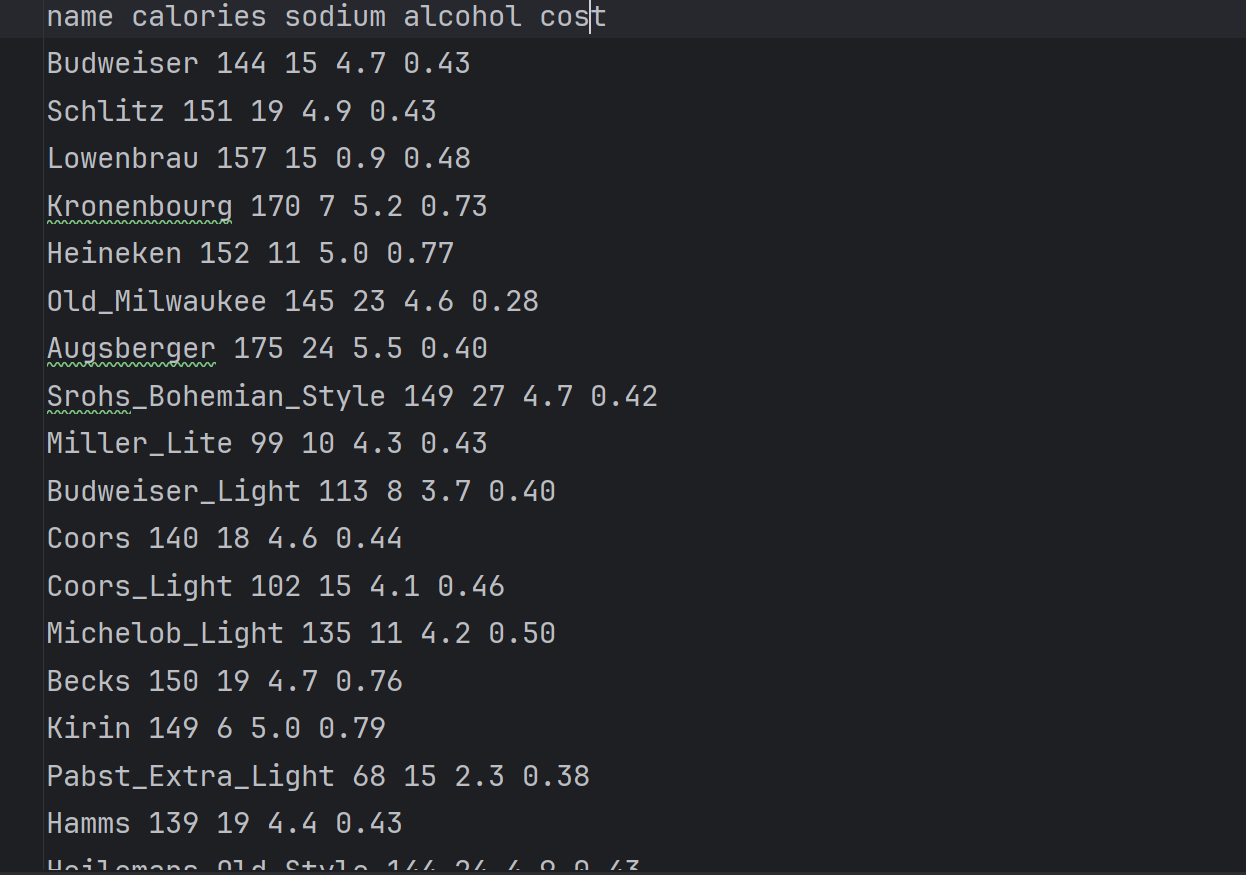
第一列的name与训练无关不要读取

python 复制代码

import pandas as pd
import numpy as np
beer = pd.read_table('data.txt',sep=' ')#注意sep划分数据
X=beer.iloc[:,1:]

2.遍历K值，计算轮廓系数选择最优K（本例K=2最佳）。

python 复制代码

from sklearn.cluster import KMeans
from sklearn import metrics
scores=[]
k=range(2,10)
for i in k:
    km=KMeans(n_clusters=i)
    km.fit(X)
    labels=km.labels_
    score=metrics.silhouette_score(X,labels)
    scores.append(score)
best_k=k[np.argmax(scores)]
print('best_k=',best_k)

3.训练模型并输出聚类标签。

python 复制代码

km=KMeans(n_clusters=best_k)
km.fit(X)
labels=km.labels_
beer['cluster']=labels
beer.sort_values('cluster',inplace=True)
print('轮廓系数: ',metrics.silhouette_score(beer.iloc[:,1:5],beer.cluster))

4.完整代码

python 复制代码

import pandas as pd
import numpy as np
beer = pd.read_table('data.txt',sep=' ')#注意sep划分数据
X=beer.iloc[:,1:]

from sklearn.cluster import KMeans
from sklearn import metrics
scores=[]
k=range(2,10)
for i in k:
    km=KMeans(n_clusters=i)
    km.fit(X)
    labels=km.labels_
    score=metrics.silhouette_score(X,labels)
    scores.append(score)
best_k=k[np.argmax(scores)]
print('best_k=',best_k)
km=KMeans(n_clusters=best_k)
km.fit(X)
labels=km.labels_
beer['cluster']=labels
beer.sort_values('cluster',inplace=True)
print('轮廓系数: ',metrics.silhouette_score(beer.iloc[:,1:5],beer.cluster))

机器学习 K-Means聚类 无监督学习

一.K-Means 聚类：从原理到实践的完整指南

1.什么是 K-Means 聚类？

应用场景举例

2.无监督学习与有监督学习的区别

3.K-Means 算法的核心原理

4.K-Means 算法的步骤详解

可视化理解

5.K-Means的评价指标(轮廓系数)

6.K-Means 的优缺点分析

优点

缺点

7.如何选择合适的 K 值？

1. 肘部法（Elbow Method）

2. 轮廓系数（Silhouette Score）

K-Means 的改进算法

总结

二.案例实现（酒类数据聚类）

1.K-Means参数

2.读取数据

2.遍历K值，计算轮廓系数选择最优K（本例K=2最佳）。

3.训练模型并输出聚类标签。

4.完整代码

机器学习 K-Means聚类无监督学习