用Python来学微积分30-微分方程初步

文章目录

• • 一、微分方程的基本概念
  • • [1.1 什么是微分方程？](#1.1 什么是微分方程？)
    • [1.2 微分方程的解](#1.2 微分方程的解)
  • 二、可分离变量的微分方程
  • • [2.1 基本形式与解法](#2.1 基本形式与解法)
    • [2.2 实例详解](#2.2 实例详解)
  • 三、初值问题
  • 四、实际应用案例
  • • [4.1 投资复利问题](#4.1 投资复利问题)
    • [4.2 曲线切线问题](#4.2 曲线切线问题)
  • 五、微分方程的数值解法
  • 总结

一、微分方程的基本概念

在我们研究的许多实际问题中，变量之间的函数关系往往不能直接建立，但我们却可以建立这些变量与它们的变化率之间的关系式。这样的关系式就是微分方程，它蕴含着变化的内在规律。

1.1 什么是微分方程？

微分方程 是含有未知函数导数或微分的方程。如果未知函数是一元函数，则称为常微分方程 （ODE）；如果未知函数是多元函数，则称为偏微分方程（PDE）。

微分方程的阶数由方程中出现的未知函数的最高阶导数的阶数决定。例如：

• d A ( t ) d t = r A ( t ) \frac{dA(t)}{dt}=rA(t) dtdA(t)=rA(t) 是一阶微分方程
• d 2 y d x 2 − 2 y = e x \frac{d^{2}y}{dx^{2}} - 2y = e^{x} dx2d2y−2y=ex 是二阶微分方程
• y ′ ′ ′ − 4 y ′ ′ + 6 y ′ = 5 y''' - 4y'' + 6y' = 5 y′′′−4y′′+6y′=5 是三阶微分方程

1.2 微分方程的解

满足微分方程的函数称为该微分方程的解。解可以分为两类：

• 通解：含有任意常数的解，且任意常数的个数等于微分方程的阶数，并且这些任意常数是相互独立的（即它们不能合并而减少个数）
• 特解：确定了通解中任意常数后得到的解

初值条件 用于确定通解中的任意常数，求微分方程满足初值条件的解的问题称为初值问题。

需要特别注意的是，​通解并不一定包含微分方程的所有解​。例如，方程 ( y ′ ) 2 − 4 y = 0 (y')^2-4y=0 (y′)2−4y=0 有通解 y = ( x + C ) 2 y=(x+C)^2 y=(x+C)2，但解 y = 0 y=0 y=0 并不包含在这个通解形式中

二、可分离变量的微分方程

2.1 基本形式与解法

形如 g ( y ) d y = f ( x ) d x g(y)dy = f(x)dx g(y)dy=f(x)dx 的微分方程称为可分离变量的微分方程 。这类方程的特点是可以将含 x x x的项和含 y y y的项分离到等号两边。

求解方法很简单：两边同时积分 ∫ g ( y ) d y = ∫ f ( x ) d x \int g(y)dy = \int f(x)dx ∫g(y)dy=∫f(x)dx

设 G ( y ) G(y) G(y)、 F ( x ) F(x) F(x) 分别是 g ( y ) g(y) g(y)、 f ( x ) f(x) f(x) 的一个原函数，则通解为： G ( y ) = F ( x ) + C G(y) = F(x) + C G(y)=F(x)+C 其中 C C C 为任意常数。

2.2 实例详解

例1 ：求解 d y d x = 2 x y \frac{dy}{dx} = 2xy dxdy=2xy

手动求解：

1. 分离变量： 1 y d y = 2 x d x \frac{1}{y}dy = 2xdx y1dy=2xdx（假设 y ≠ 0 y \neq 0 y=0）
2. 两边积分： ∫ 1 y d y = ∫ 2 x d x \int \frac{1}{y}dy = \int 2xdx ∫y1dy=∫2xdx
3. 得到： ln ⁡ ∣ y ∣ = x 2 + C 1 \ln|y| = x^2 + C_1 ln∣y∣=x2+C1
4. 整理： y = ± e x 2 + C 1 = ± e C 1 e x 2 = C e x 2 y = \pm e^{x^2 + C_1} = \pm e^{C_1}e^{x^2} = Ce^{x^2} y=±ex2+C1=±eC1ex2=Cex2（其中 C为任意非零常数）
5. 检验 y=0的情况：将 y=0代入原方程，两边均为0，故 y=0也是解，对应 C=0的情况
6. 因此，通解为 y = C e x 2 y=Ce^{x^2} y=Cex2（C为任意常数）​，这包含了 y=0的情况

Python求解：

import sympy as sp

x, y = sp.symbols('x y')
y_func = sp.Function('y')
eq = sp.Eq(y_func(x).diff(x), 2*x*y_func(x))
solution = sp.dsolve(eq)
print(solution)

Python代码执行结果：

Eq(y(x), C1*exp(x**2))

例2 ：求解 d y d x = 2 x ( 1 + y 2 ) \frac{dy}{dx}=2x(1 + y^{2}) dxdy=2x(1+y2)

手动求解：

1. 分离变量： 1 1 + y 2 d y = 2 x d x \frac{1}{1 + y^{2}}dy = 2xdx 1+y21dy=2xdx
2. 两边积分： ∫ 1 1 + y 2 d y = ∫ 2 x d x \int\frac{1}{1 + y^{2}}dy=\int 2xdx ∫1+y21dy=∫2xdx
3. 得到： arctan ⁡ y = x 2 + C \arctan y = x^{2} + C arctany=x2+C
4. 整理： y = tan ⁡ ( x 2 + C ) y = \tan(x^{2} + C) y=tan(x2+C)

Python求解：

import sympy as sp

x, y = sp.symbols('x y')
y_func = sp.Function('y')
eq = sp.Eq(y_func(x).diff(x), 2*x*(1 + y_func(x)**2))
solution = sp.dsolve(eq)
print(solution)

Python代码执行结果：

Eq(y(x), tan(C1 + x**2))

三、初值问题

初值问题是求微分方程满足给定初始条件的特解的问题。例如： { d y d x = y x y ∣ x = 1 = 2 \begin{cases} \frac{dy}{dx} = \frac{y}{x} \\ y|_{x = 1} = 2 \end{cases} {dxdy=xyy∣x=1=2

手动求解步骤：

1. 分离变量： 1 y d y = 1 x d x \frac{1}{y}dy = \frac{1}{x}dx y1dy=x1dx
2. 两边积分： ln ⁡ ∣ y ∣ = ln ⁡ ∣ x ∣ + C \ln|y| = \ln|x| + C ln∣y∣=ln∣x∣+C
3. 整理得通解： y = C x y = Cx y=Cx（此处 C = ± e C 1 C = \pm e^{C_1} C=±eC1）
4. 代入初值条件 y ∣ x = 1 = 2 y|_{x=1} = 2 y∣x=1=2： 2 = C ⋅ 1 2 = C \cdot 1 2=C⋅1，得 C = 2 C = 2 C=2
5. 特解为： y = 2 x y = 2x y=2x

Python求解：

import sympy as sp

x = sp.symbols('x')
y = sp.Function('y')
eq = sp.Eq(y(x).diff(x), y(x)/x)
# 定义初值条件：当x=1时，y=2
solution = sp.dsolve(eq, ics={y(1): 2})
print(solution)

Python代码执行结果：

Eq(y(x), 2*x)

四、实际应用案例

4.1 投资复利问题

问题 ：假设以本金 A 0 A_0 A0 进行投资，年利率为 r r r，以连续复利计算，求 t t t 年末的本利和。

建模 ： 设 t t t 时刻的本利和为 A ( t ) A(t) A(t)，则资金变化率等于该时刻资金获取的利息： d A ( t ) d t = r A ( t ) \frac{dA(t)}{dt} = rA(t) dtdA(t)=rA(t)

求解：

1. 分离变量： d A ( t ) A ( t ) = r d t \frac{dA(t)}{A(t)} = rdt A(t)dA(t)=rdt
2. 两边积分： ∫ d A ( t ) A ( t ) = ∫ r d t \int \frac{dA(t)}{A(t)} = \int rdt ∫A(t)dA(t)=∫rdt
3. 得到： ln ⁡ A ( t ) = r t + C \ln A(t) = rt + C lnA(t)=rt+C
4. 整理： A ( t ) = e r t + C = C e r t A(t) = e^{rt + C} = Ce^{rt} A(t)=ert+C=Cert
5. 代入 A ( 0 ) = A 0 A(0) = A_0 A(0)=A0： A 0 = C e 0 = C A_0 = Ce^0 = C A0=Ce0=C
6. 特解： A ( t ) = A 0 e r t A(t) = A_0e^{rt} A(t)=A0ert

Python计算示例：

import numpy as np

A0 = 1000  # 初始本金
r = 0.05   # 年利率
t = 10     # 投资年限
A_t = A0 * np.exp(r * t)
print(f"{t}年后的本利和为：{A_t:.2f}元")

Python代码执行结果：

10年后的本利和为：1648.72元

4.2 曲线切线问题

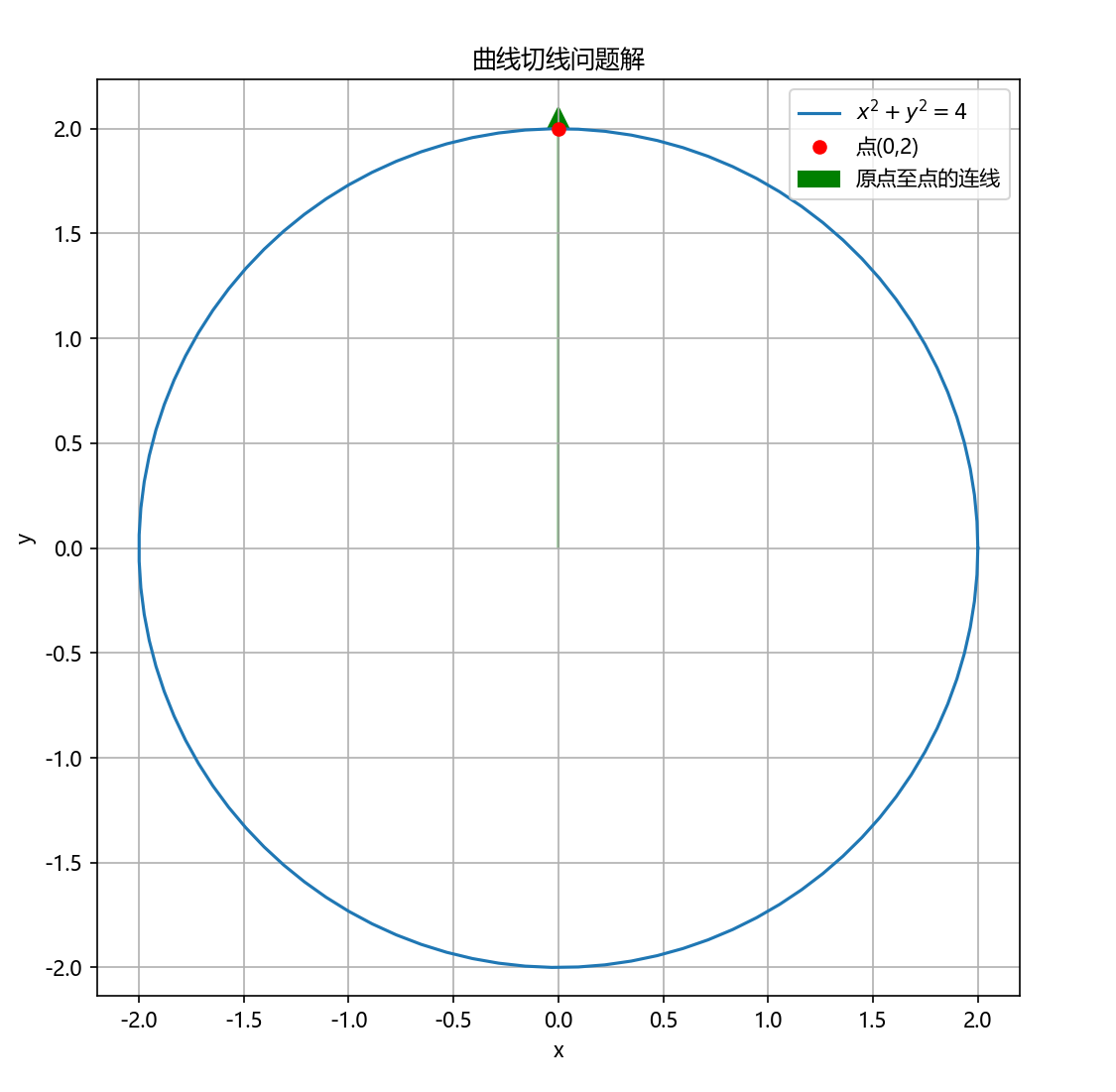
问题 ：在 x O y xOy xOy 平面上，求过点 ( 0 , 2 ) (0, 2) (0,2) 的曲线 y = y ( x ) y = y(x) y=y(x)，使曲线上任一点 ( x , y ) (x, y) (x,y) 处的切线与坐标原点 O O O 到点 ( x , y ) (x, y) (x,y) 的连线垂直。

建模 ： 曲线在点 ( x , y ) (x, y) (x,y) 处的切线斜率为 d y d x \frac{dy}{dx} dxdy，原点 O O O 到点 ( x , y ) (x, y) (x,y) 的连线斜率为 y x \frac{y}{x} xy。由于两者垂直，斜率乘积为 -1： d y d x ⋅ y x = − 1 ⇒ d y d x = − x y \frac{dy}{dx} \cdot \frac{y}{x} = -1 \quad \Rightarrow \quad \frac{dy}{dx} = -\frac{x}{y} dxdy⋅xy=−1⇒dxdy=−yx

求解：

1. 分离变量： y d y = − x d x ydy = -xdx ydy=−xdx
2. 两边积分： ∫ y d y = − ∫ x d x \int ydy = -\int xdx ∫ydy=−∫xdx
3. 得到： 1 2 y 2 = − 1 2 x 2 + C \frac{1}{2}y^2 = -\frac{1}{2}x^2 + C 21y2=−21x2+C
4. 整理： x 2 + y 2 = C x^2 + y^2 = C x2+y2=C（其中 C = 2 C 1 C = 2C_1 C=2C1）
5. 代入点 ( 0 , 2 ) (0, 2) (0,2)： 0 2 + 2 2 = C 0^2 + 2^2 = C 02+22=C，得 C = 4 C = 4 C=4
6. 曲线方程： x 2 + y 2 = 4 x^2 + y^2 = 4 x2+y2=4

Python绘图：

import matplotlib.pyplot as plt
import numpy as np

theta = np.linspace(0, 2*np.pi, 100)
x = 2 * np.cos(theta)  # 半径为2的圆的参数方程
y = 2 * np.sin(theta)

plt.figure(figsize=(8, 8))
plt.plot(x, y, label='$x^2 + y^2 = 4$')
plt.plot(0, 2, 'ro', label='点(0,2)')
plt.arrow(0, 0, 0, 2, head_width=0.1, head_length=0.1, fc='g', ec='g', 
          label='原点至点的连线')
plt.axis('equal')
plt.grid(True)
plt.xlabel('x')
plt.ylabel('y')
plt.title('曲线切线问题解')
plt.legend()
plt.show()

Python代码执行结果：

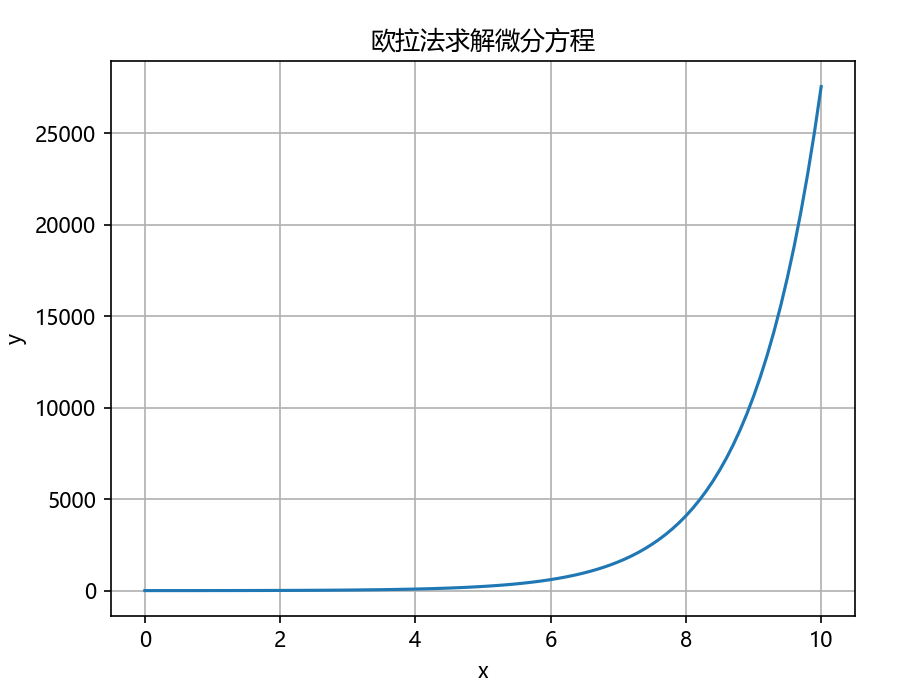
五、微分方程的数值解法

当微分方程难以求得解析解时，我们可以采用数值解法。欧拉法是最基本的数值解法之一：

import numpy as np
import matplotlib.pyplot as plt

def euler_method(f, x0, y0, h, n):
    """
    欧拉法求解微分方程
    f: 微分方程dy/dx = f(x, y)
    x0, y0: 初始条件
    h: 步长
    n: 步数
    """
    x = np.zeros(n+1)
    y = np.zeros(n+1)
    x[0] = x0
    y[0] = y0
    
    for i in range(n):
        y[i+1] = y[i] + h * f(x[i], y[i])
        x[i+1] = x[i] + h
    
    return x, y

# 示例：求解dy/dx = x + y, y(0)=1
def f(x, y):
    return x + y

x, y = euler_method(f, 0, 1, 0.1, 100)
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
plt.title('欧拉法求解微分方程')
plt.grid(True)
plt.show()

Python代码执行结果：

总结

微分方程作为描述变化规律的有力工具，在数学和实际问题中有着广泛应用。通过本文的学习，我们了解了：

1. 微分方程的基本概念：阶数、通解、特解等
2. 可分离变量方程的解法：分离变量再积分
3. 初值问题的求解：代入初始条件确定特解
4. 实际应用：从复利计算到几何问题

Python中的Sympy库为微分方程的求解提供了便利工具，结合数值方法可以解决更复杂的实际问题。微分方程的学习为我们理解动态系统、连续变化过程奠定了坚实基础。

---

往期精彩回顾：

• 用Python来学微积分27-曲线的渐近线
• 用Python来学微积分28-泰勒公式

专栏导航目录 《程序员AI之路：从Python起步》完全学习导航

完整代码已开源 ai-learning-path，欢迎Star和Fork！

下期预告：在下一篇文章中，我们将开始学习定积分。

---

参考资料：

1. 扈志明《微积分》教材

互动邀请：如果你对本章内容有独特的理解或在实际应用中遇到过有趣的问题，欢迎在评论区分享交流！