机器学习--决策树

一、决策树分类算法

决策树是一种监督学习算法，用于分类和回归任务。它通过从数据集中学习规则来预测目标变量的值。决策树模型以树的形式表示，其中内部节点代表特征或属性上的测试，分支代表测试结果，而叶节点代表类别（对于分类任务）或输出值（对于回归任务）
决策树的主要组成部分：
- 根节点：决策树的根节点是整棵树的起点，即第一个判断特征的节点
- 内部节点：代表一个特征或属性
- 分支：每个内部节点连接着一些分支，每个分支代表着某个特征取值，表示样本在该特征上的取值
- 叶节点：没有子节点的节点，表示最终的决策结果
- 决策树的深度：所有节点的最大层次数
- 决策规则：决策树的每个节点表示一条决策规则，即对某个特征的判断，其决策规则是由已知数据集计算而得的
- 剪枝：决策树为了避免过度拟合（Overfitting），通常会在构建好树之后进行剪枝操作，即去掉一些决策规则，以避免模型过于复杂
决策树的优点：
- 可以可视化
- 对数据的准备要求不高
- 能够处理非数值型数据
决策树的缺点：
- 容易过拟合，通常需要剪枝技术
选择一个合适的特征作为判断节点，可以快速的分类，减少决策树的深度。决策树的目标就是把数据集按对应的类标签进行分类。最理想的情况是，通过特征选择能把不同类别的数据集贴上对应类标签。特征选择的目标使得分类后的数据集比较纯，如何衡量一个数据集纯度，常见的决策树算法：
- ID3算法：ID3（Iterative Dichotomiser 3）算法是决策树算法中最早的一种，使用信息增益来选择最优特征。ID3算法基于贪心思想，一直选择当前最优的特征进行分割，直到数据集分割完成或没有特征可分割为止
- C4.5算法：C4.5算法是ID3算法的改进版，使用信息增益比来选择最优特征。C4.5算法对ID3算法中存在的问题进行了优化，包括处理缺失值、处理连续值等
- CART算法：CART（Classification and Regression Trees）算法是一种基于基尼不纯度的二叉树结构分类算法，用于解决二分类和回归问题。CART算法可以处理连续值和离散值的特征，能够生成二叉树结构，具有较好的可解释性

1、ID3 算法

ID3（Iterative Dichotomiser 3）算法是由Ross Quinlan开发的一种决策树学习算法，主要用于分类任务。ID3算法的目标是从训练数据集中推断出一个决策树模型，使得该模型可以用于预测新的数据实例的类别标签
ID3 算法只能用于处理离散属性。如果数据集中包含连续属性，则需要先进行离散化处理
ID3算法的基本步骤：
- 计算根节点的信息熵
- 计算信息增益：对于数据集中的每一个属性，计算其信息增益
- 选择最佳属性：选择具有最高信息增益的属性作为当前节点
- 创建子节点：根据所选属性的不同值创建子节点
- 递归构建子树：对每个子节点，重复上述过程，直到所有实例都属于同一类别或无法继续分裂为止

1.1 信息熵

信息熵（Information Entropy）：用来衡量数据集中的不确定性或信息的混乱程度，在机器学习中可以衡量数据的纯度
对于一个二元分类问题，熵可以定义为：假设样本集合 D 共有 N 类，其中类别 i 在数据集 D 中的概率是 P(i)：

H(D)=−\\sum_{i=1}\^{n}P(i)log_2P(i)

信息熵越大，数据的不确定性越大，信息就越多；信息熵越小，数据的不确定性越小，比如：
- 数据 A = {1,2,3,4,5,6,7,8}，数据 B = {1,1,1,1,2,2,2,2}，数据 A 包含了 8 中信息，数据 B 包含了 2 中信息，那么数据 A 的信息熵大于数据 B

1.2 信息增益

信息增益（Information Gain）：特征 A 对训练数据集 D 的信息增益 G(D,A)，定义为集合 D 的熵 H(D) 与特征 A 给定条件下 D 的熵H(D|A)之差，即信息增益=熵 - 条件熵，选择最大的信息增益特征来构建决策树

G(D,A)=H(D)−H(D\|A)

**案例：**根据以下信息构建一棵预测是否批准贷款的决策树。我们可以看到有 3 个影响因素：工作、房、信誉

样本	工作	房	信誉	贷款结果
1	是	是	好	批准
2	否	是	不好	批准
3	是	否	不好	批准
4	否	是	不好	批准
5	否	是	一般	拒绝
6	是	是	一般	批准
7	否	否	好	拒绝
8	否	否	一般	拒绝

2、CART 算法

CART（Classification And Regression Trees）算法是一种用于构建决策树的算法，它可以用于分类任务和回归任务
CART 决策树使用基尼指数来选择划分属性
- 分类树：基尼指数最小准则
- 回归树：平方误差最小准则

1.1 分类树

基尼指数是用于评估数据集纯度的一种度量。基尼指数越低，数据集越纯净。对于给定的数据集 D，其基尼指数定义为：其中 $P_k$ 是类 K 在数据集 D 中的比例。如果数据集中只有一个类，那么𝐺𝑖𝑛𝑖(𝐷)=0

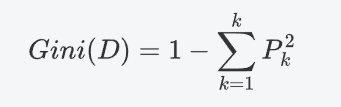
在每个节点，CART 算法选择使得基尼指数最小化的特征来进行分裂。对于二叉分裂，假设特征 A 有 t 个不同的值，则可以产生 t-1 个可能的分裂点。对于每个分裂点，计算分裂后的两个子集的基尼指数，并选取基尼指数最小的分裂点
CART分类树的构建步骤：
- 计算基尼指数：对于每个特征，计算其所有可能的分割点产生的基尼指数
- 选择最佳分割点：选择使得分割后基尼指数最小的特征和分割点
- 分割数据集：根据最佳分割点将数据集分成两个子集
- 递归构建子树：对每个子集重复上述过程，直到满足停止条件
- 停止条件：当子集中的所有样本属于同一类，或者子集的大小小于预设的最小叶子节点大小，或者达到了最大深度时，停止分裂，将当前子集作为一个叶节点

案例：

样本	工作	房	信誉	贷款结果
1	是	是	好	批准
2	否	是	不好	批准
3	是	否	不好	批准
4	否	是	不好	批准
5	否	是	一般	拒绝
6	是	是	一般	批准
7	否	否	好	拒绝
8	否	否	一般	拒绝

1.2 回归树

在回归任务中，CART 算法试图最小化均方误差。对于给定的数据集 D，其均方误差定义为：其中 $y_i$ 是第 i 个样本的真实值， $\\hat{y_D}$ 是数据集 D 的平均响应值

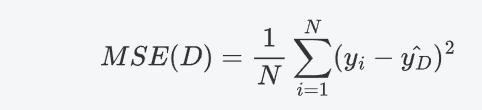
在构建回归树时，CART算法选择使得均方误差最小化的特征来进行分裂。同样，对于每个特征值，寻找最佳的分裂点，使得分裂后的两个子集的均方误差之和最小

3、API

DecisionTreeClassifier 是 scikit-learn 库中的一个类，用于创建决策树分类器，DecisionTreeClassifier()用来创建决策树模型实例，参数如下：
- criterion (str, default="gini")：
  - gini：使用基尼不纯度
  - entropy：使用信息熵
- max_depth (int, default=None)：
  - 树的最大深度。如果设置为 None，则节点会被扩展直到所有的叶子都是纯净的或直到所有的叶子包含少于 min_samples_split 个样本

复制代码

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeClassifier, export_graphviz

def iris_decisionTreeClassifier():
    iris = load_iris()
    data = iris.data
    target = iris.target
    # 划分数据集
    X_train, X_test, y_train, y_test = train_test_split(data, target, test_size=0.3, random_state=42)
    # 特征工程：标准化
    ss = StandardScaler()
    X_train = ss.fit_transform(X_train)
    X_test = ss.transform(X_test)
    # 创建决策树模型
    model = DecisionTreeClassifier(criterion="entropy", max_depth=108)
    # 训练
    model.fit(X_train, y_train)
    print(model.score(X_test, y_test))
    # 可视化
    # export_graphviz(model, out_file="titanic_tree.dot", feature_names=iris.feature_names)

补充

1. 关于根节点的选择

根节点是基尼指数最小的？

不完全对

。根节点本身是未分裂的完整数据集，它的基尼系数（或熵）反映的是

初始不纯度

。
- 关键点 ：我们不是选"基尼指数最小的节点作为根"，而是选能使分裂后子节点的加权基尼指数下降最多的属性作为根节点的分裂依据。
- 示例
  
  ：
  - 父节点（根节点初始状态）的基尼系数是0.5。
  - 用属性A分裂后，子节点的加权基尼系数降至0.2（下降0.3）；
  - 用属性B分裂后，加权基尼系数降至0.4（下降0.1）。
  - 选择属性A作为根节点的分裂属性，因为它的分裂效果更好（下降更多）。

2. 关于子节点的选择

子节点是其他属性下基尼系数下降最大的？

部分正确，但有前提

：
1. 子节点的分裂属性不一定是"其他属性"，也可能与父节点相同（尤其在连续值或多值离散属性中）。
2. 选择标准 ：在每个节点（包括子节点）上，都会重新计算所有可用属性的分裂效果（基尼下降），选择当前最优的，而非局限于"相对于根节点"。
- 示例
  
  ：
  - 根节点用Age分裂后，生成子节点"青年"。
  - 在"青年"子节点上，重新评估Income、Student等属性的分裂效果，可能发现Student的分裂效果最好（与根节点用的Age无关）。

3. 决策树分裂的核心逻辑

递归分割：每个节点的分裂都是独立的，目标是让当前节点的子节点尽可能"纯净"（即基尼指数最小）。
贪婪算法：每次分裂只考虑当前节点的最优解，不回溯或全局优化。

4. 用公式和步骤总结

步骤1 ：计算当前节点（如根节点）的基尼系数 GparentGparent。
步骤2

：对每个候选属性

AA

：
1. 按属性 AA 的可能取值分裂数据，得到子节点 DvD**v。
2. 计算子节点的加权基尼系数： Gsplit=∑v∣Dv∣∣D∣G(Dv)G split=∑v ∣D ∣∣D**v ∣G (D**v)
3. 计算基尼下降： ΔG=Gparent−GsplitΔG =G parent−Gsplit
步骤3 ：选择使 ΔGΔG 最大的属性分裂当前节点。
重复：对每个子节点递归执行上述步骤，直到满足停止条件（如最大深度、基尼下降小于阈值等）。